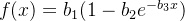一. 最小二乘曲线拟合
给定一组数据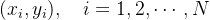
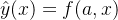
那么,最小二乘曲线拟合的目标就是:求出一组待定系数的值,使得以下表达式子最小:
在MATLAB中格式如下:
[a,jm]=lsqcurvefit(Fun,a0,x,y)
%Fun原型函数的MATLAB表示
%a0为最优化的初值
%x,y为原始输入输出的数据向量
%a为返回的待定系数向量
%jm为此待定系数下的目标函数的值例题1
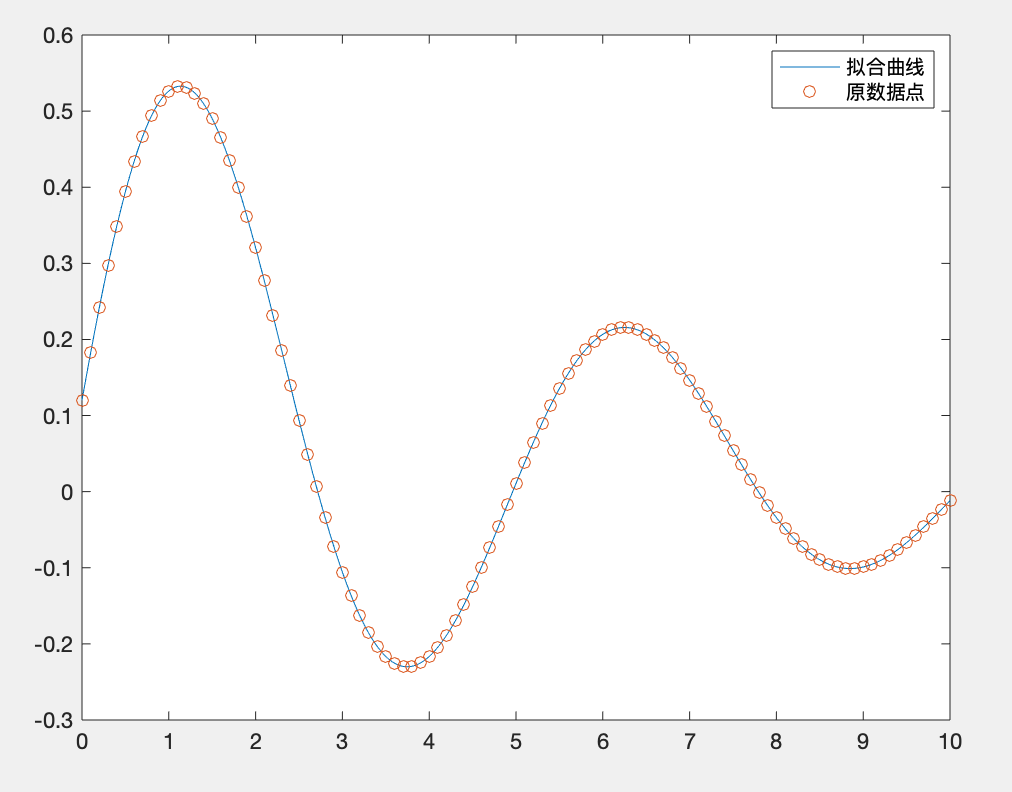
由以下MATLAB代码生成一组数据:
x=0:.1:10;
y=0.12*exp(-0.213*x)+0.54*exp(-0.17*x).*sin(1.23*x);
该组数据满足y(x),求出待定系数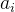
解:
MATLAB代码如下:
clc;clear;
x=0:0.1:10;
y=0.12*exp(-0.213*x)+0.54*exp(-0.17*x).*sin(1.23*x);
f=inline('a(1)*exp(-a(2)*X)+a(3)*exp(-a(4)*X).*sin(a(5)*X)','a','X');
ff=optimset;
ff.TolFun=1e-20;ff.TolX=1e-15; %修改精度限制
[xx,res]=lsqcurvefit(f,[1 1 1 1 1],x,y,[],[],ff)
%绘制曲线
x1=0:0.01:10;
y1=f(xx,x1); %代入运算
plot(x1,y1,x,y,'o');
legend('拟合曲线','原数据点')
运行结果:
xx = 0.120000000000000 0.213000000000000 0.540000000000000 0.170000000000000 1.230000000000000
res =0
例题2
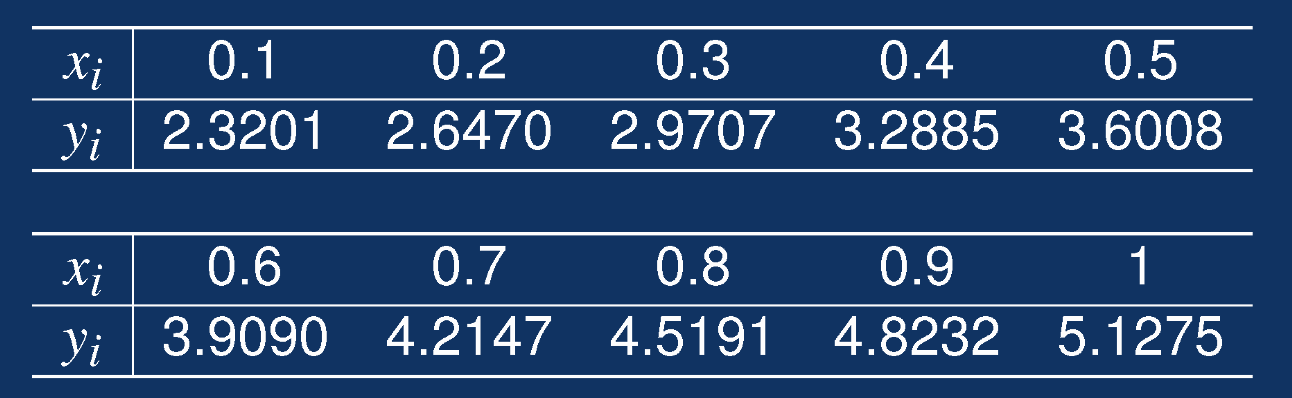
已知以下数据可能满足。求满足数据的最小二乘解a,b,c,d的值。
解:
令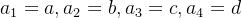
MATLAB代码如下:
clc;clear;
%输入已知参数
x=0.1:0.1:1;
y=[2.3201,2.6470,2.9707,3.2885,3.6008,3.9090,4.2147,4.5191,4.8232,5.1275];
f=inline('a(1)*X+a(2)*X.^2.*exp(-a(3)*X)+a(4)','a','X');
a=lsqcurvefit(f,[1 2 2 3],x,y)
%绘制曲线
y1=f(a,x);
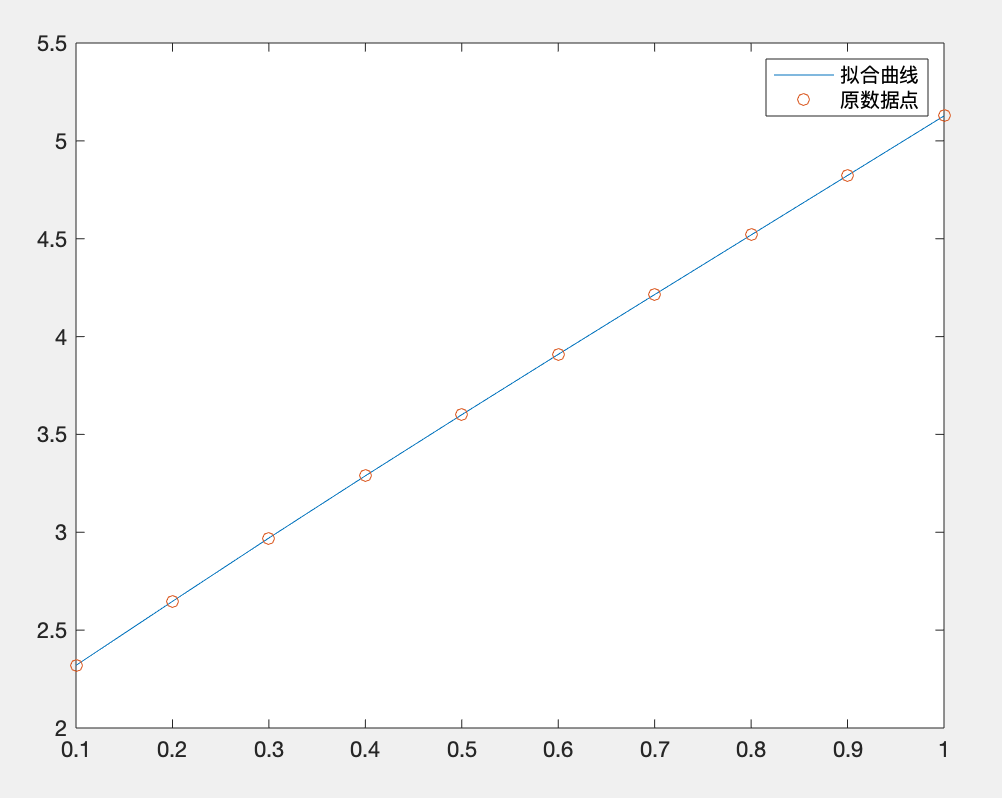
plot(x,y1,x,y,'o');
legend('拟合曲线','原数据点');运行结果:
a = 3.100076146500888 1.502655931856580 4.004634473891176 2.000013871079962
在MATLAB中,非线性拟合命令格式如下:
[beta,r,J]=nlinfit(x,y,fun,beta0)
%x,y为原始数据
%fun是在M文件中定义的函数
%beta0是函数中参数的初始值
%beta为参数的最优值
%r是各点处的拟合残差
%J为雅克比矩阵的数值初始参数beta0可以用以下方法求得:
首先观察有几个待定系数,有几个待定系数就将几组实验数据代入方程中,由此可得参数的初始值。
例题3
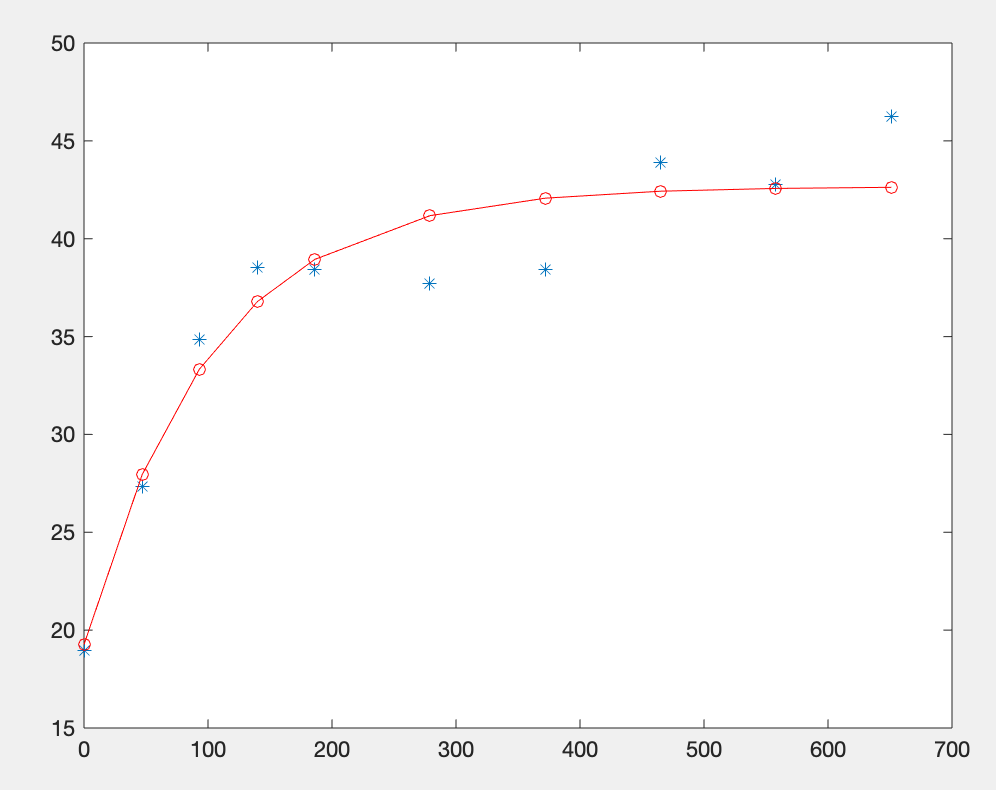
给定以下数据,利用非线性的方法求出函数f(x)的参数。
| x | 0 | 47 | 93 | 140 | 186 | 279 | 372 | 465 | 558 | 651 |
| y | 18.98 | 27.35 | 34.86 | 38.52 | 38.44 | 37.73 | 38.43 | 43.87 | 42.77 | 46.22 |
解:
MATLAB代码如下:
clc;clear;
x=[0 47 93 140 186 279 372 465 558 651];
y=[18.98 27.35 34.86 38.52 38.44 37.73 38.43 43.87 42.77 46.22];
b0=[43 0.6 0.1]; %初始参数值
fun=inline('b(1)*(1-b(2)*exp(-b(3)*X))','b','X');
[b,r,j]=nlinfit(x,y,fun,b0); %b为最佳参数
b
R=sum(r.^2) %误差平方和
y1=fun(b,x);
plot(x,y,'*',x,y1,'-or')运行结果:
b =42.664037023023802 0.548346447450711 0.009880232273427
R =46.197464448828995
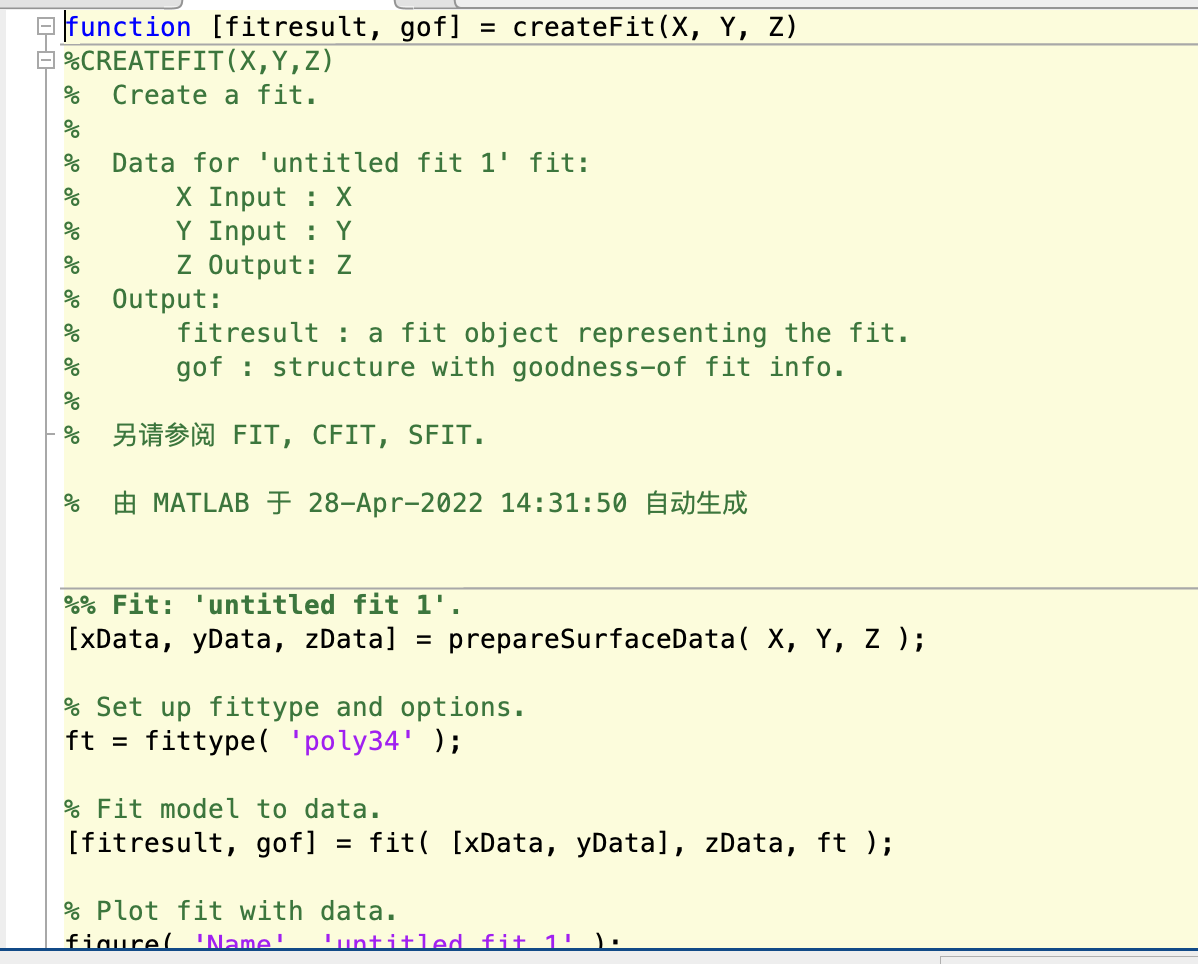
二. curve fitting tool工具
以下将通过一个例子,来理解MATLAB中curve fitting tool工具。
首先在新建的脚本文件编辑框中键入以下代码:
clc;clear;
%产生数据
x=-20:2:20;
y=-20:2:20;
[X,Y]=meshgrid(x,y);
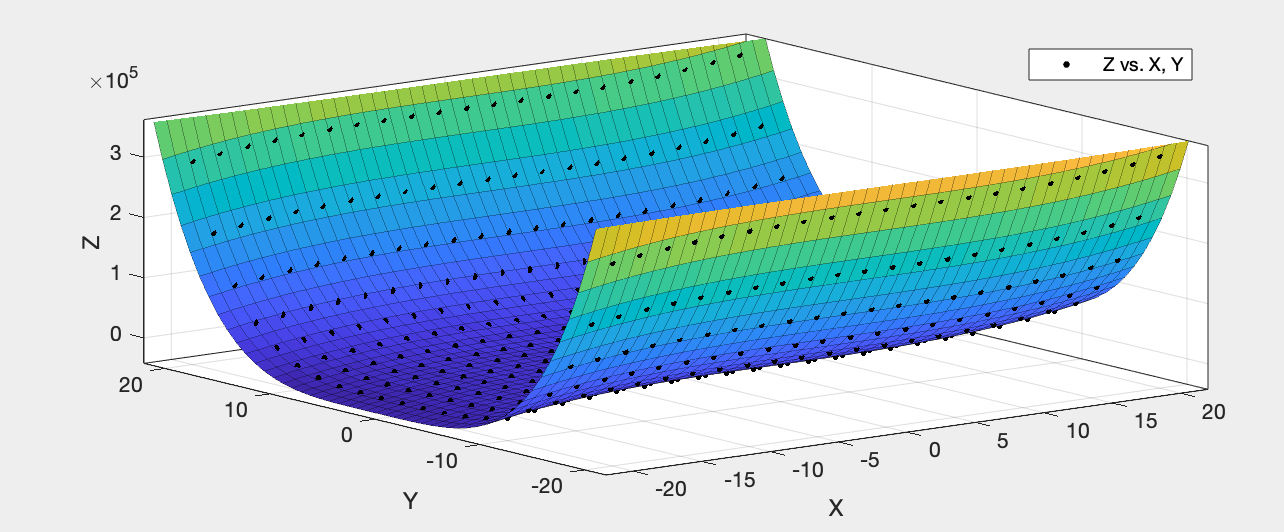
Z=3*X.^3-4*X+2*Y.^4+3*Y^3;
meshgrid(X,Y,Z);第一步
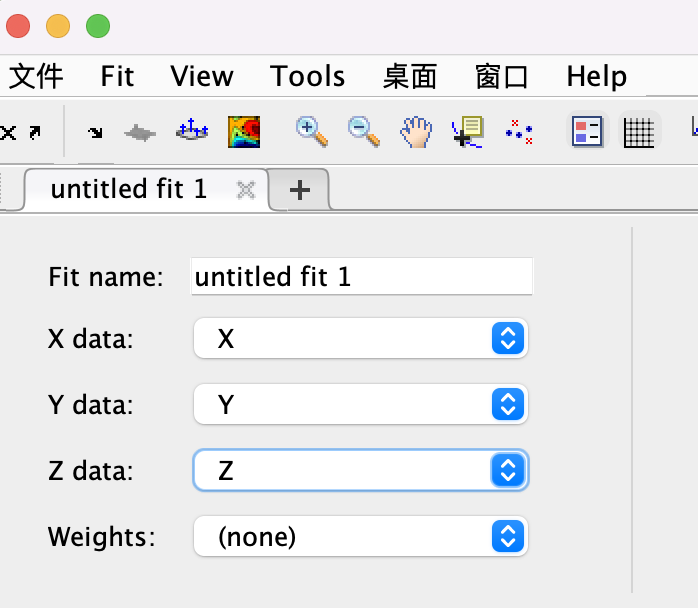
在APP选项框中打开curve fitting 工具,选择数据源X/Y/Z data
第二步
选择合适的拟合方法。本例子待拟合的曲面为多项式,所以可以直接选择。其他可选择的拟合类型,如下:
- Custom Equation:用户自定义的函数类型
- Interpolant:插值逼近,有四种类型,linear、nearest、neighbor、cubic spline、shape-preserving
- Lowess:平滑逼近,局部加权回归
- Polynomial:多项式逼近,有9种类型,linear,quadratic,cubic,4-9th degree
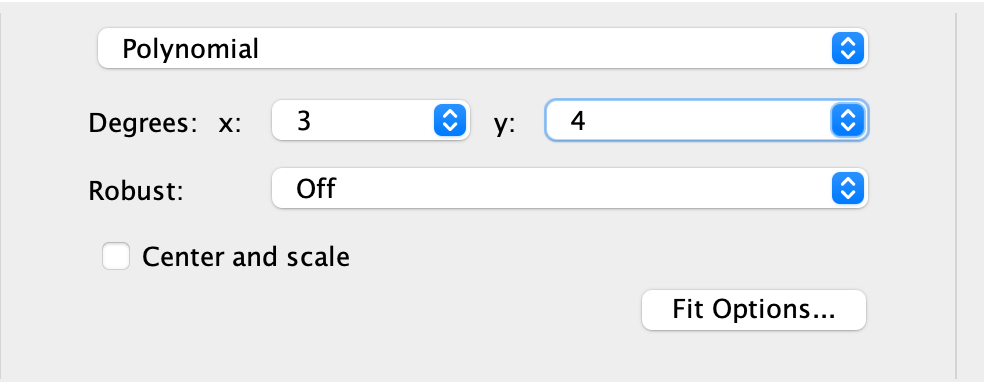
第三步
选择合适的多项式次数与系数
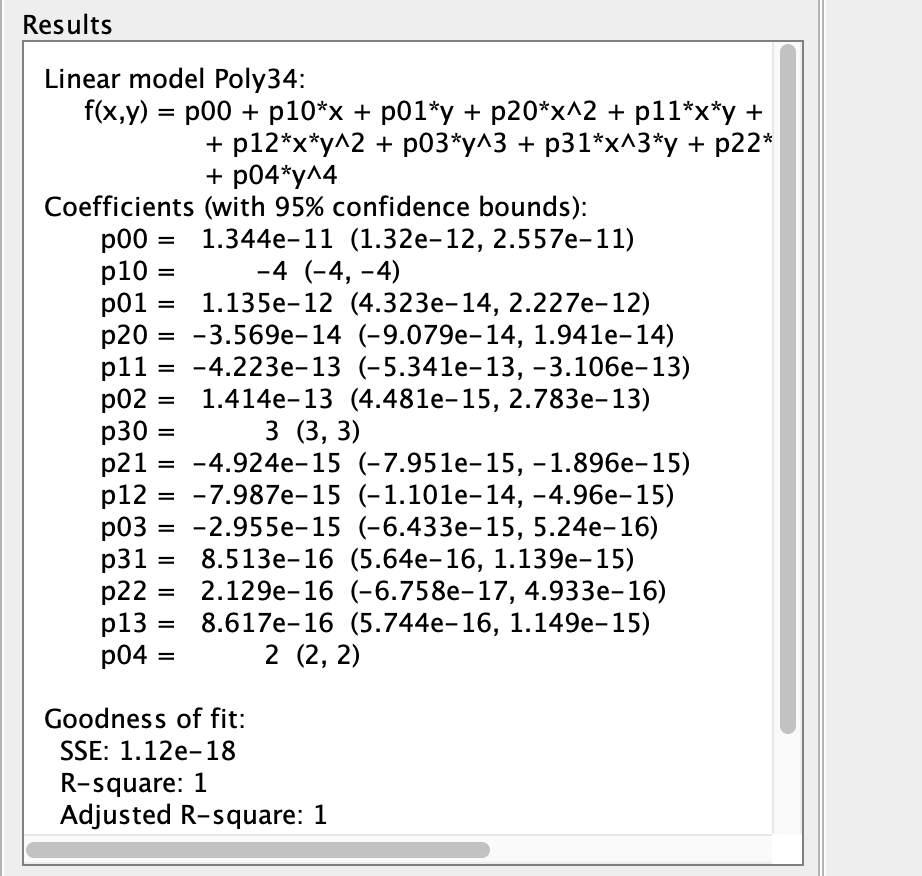
第四步
拟合后的结果信息在Fitting对话框中的Results文本框中,此处有此次拟合的主要统计信息,包含:
- 误差平方和 SSE:该参数计算拟合参数后的回归值与原始数据对应点的误差平方和,类比方差
- 确定系数 R-square
- 调整后的确实系数 Adjusted R-square
- RMSE:该参数是预测数据和原始数据对应点误差的平方和的均值的平方根,即均方误差,类比标准差
另外附加两个功能:
生成代码:文件>>Generate Code>>自动生成一个creatFit.m文件;
生成图片:文件>>Print to figure
![J=min\sum_{i=1}^N[y_i-\hat y(x_i)]^2=min\sum_{i=1}^N[y_i-f(a,x_i)]^2](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9KJTNEbWluJTVDc3VtXyU3QmklM0QxJTdEJTVFTiU1QnlfaS0lNUNoYXQlMjB5JTI4eF9pJTI5JTVEJTVFMiUzRG1pbiU1Q3N1bV8lN0JpJTNEMSU3RCU1RU4lNUJ5X2ktZiUyOGElMkN4X2klMjklNUQlNUUy)