本来是想讲BERT的,但是BERT的重点是部署应用,而且用BERT跑一些NLP领域的很多任务时,一般做法都是BERT后面再串一个概率模型来约束输出,比如串联一个条件随机场CRF模型。而我们还没讲CRF呢,而且要了解CRF需要首先了解隐马尔可夫模型HMM(Hidden Markov Model),但HMM又牵扯了好几个比较晦涩的算法,比如前向、后向算法、维特比解码算法(viterbi algorothm)、EM算法等,内容有点难也有点多,所以这里我单独针对HMM和CRF写一两个章节,为BERT铺个垫。
九、隐马尔可夫模型 HMM (Hidden Markov Model)
隐马尔可夫模型,HMM (Hidden Markov Model),是一个拟合序列数据的概率模型,也叫统计模型,是用来描述马尔可夫过程的模型。本章节从原理、手动计算、调包实现,三方面来说清楚HMM。
(一)HMM的原理
网上搜HMM,大部分文章一上来就整篇整篇的数学推导,随意晦涩大量的符号和脚标,让大部分读者上来就一脸懵。我最讨厌这种卖弄了,其实底层的数学没那么难理解,搞一堆数学符号让人抓狂。本篇通过一个最通俗的例子,来抽取HMM的底层原理。
1、做一个简单的小概率题
这个概率题就是HMM的概型,理解了这道题你就理解了HMM。我拿这道题来对比理解HMM。
这道题的解答案其实不难,就是一系列概率的相乘相加,但我们的目的是从它抽取HMM的原理。所以我们先不急着解题。
这道题最大的难点可能就是有的人不理解矩阵A和矩阵B。这里我先解释一下:
(1)我们先按行看矩阵A:
第一行的0.5表示:我前一次是从盒子1中抽球的,那我这一次还从盒子1中抽球的概率。
第一行的0.4表示:我前一次是从盒子1中抽球的,那我这一次从盒子2中抽球的概率。
第一行的0.1表示:我前一次是从盒子1中抽球的,那我这一次从盒子3中抽球的概率。同理A矩阵的第二行、第三行:
第二行就表示:我前一次是从盒子2中抽球的,那我这一次去盒子1、盒子2、盒子3中抽取的概率。
第三行就表示:我前一次是从盒子3中抽球的,那我这一次去盒子1、盒子2、盒子3中抽取的概率。所以,矩阵A的每行3个数字之和都是1。
而且A矩阵是一个方阵,就是行数=列数=盒子的种类数
(2)矩阵B就更好理解了,矩阵B的第一行表示我已经抽取的是盒子1,那我抽取白球的概率就是0.4,抽取黑球的概率就是0.6了,因为第一个盒子只有4白6黑嘛。同理矩阵B的第二行和第三行。所以矩阵B的每行数字之和也是1。但是B矩阵的行数=盒子的种类数,列数=小球的种类数。
2、从上面的概率题,抽出HMM概型
(1)从上面的概率题,抽取HMM中的相关概念:
一是,上题中的盒1盒2盒3,对应在HMM中就是隐含状态(states)。对应下图A处。
二是,上题中的最后抽取的序列是“白黑白白黑”,这个序列叫观测序列(observations),也叫可见状态链,对应下图C处。
三是,由于每次抽取的小球的颜色的概率不仅取决于,小球所在的盒子中的黑白球的比例,还取决于你是从哪个盒子中抽的,所以其实观测序列还对应着一个隐含状态序列,就是下图的B处(说明:B只是我胡乱做的一个隐藏状态序列,真实的B可能不是这个序列)。这个隐藏状态序列叫隐藏状态链。
意思就是我们是可以观测到小球颜色序列,但是观测不到每次小球都是从哪个盒子中取的,也就是观测不到盒子序列。但是我们可以肯定的是:当我们得到“白黑白白黑”这个序列时,一定是存在一个对应的盒子序列的,虽然我们观测不到这个盒子序列,但它是真实存在的。这就好比我们只能看到股票的涨涨跌跌,但我们看不到涨跌背后的原因,但是我们笃定涨跌背后肯定是有原因的。
四是,上题的观测序列长度=隐藏状态序列长度=5。其实现实很多问题中,二者不一定非得相等。
可见:一个隐马尔科夫链,其实是一个双链条!一条C链条,另一条B链条。
而且B链和C链都是一个随机过程,所以隐马尔可夫链也是一个双重随机过程。也就是一个HMM有两个随机序列。
在很多现实问题中,有些现象不符合隐马尔可夫过程,但人们会通过扩展"可观测"和"隐藏"状态的概念来构造一个HMM过程,然后用HMM来拟合实际问题。一般我们的做法是:把C当成"果",把对应的B当成"因"。先寻找多种"因",并总结出因与因之间的关系(就是矩阵A)、因与果之间的关系(就是矩阵B),C又是可观测到的,就可以用HMM进行拟合了。
(2)从上面的概率题,抽取HMM中的两个假设
隐马尔科夫模型有两个基本假设:
一是,有限状态马尔科夫性假设(First-Order Markov Assumption):
这个假设表明,系统在某个时间点的状态只依赖于前一个时间点的状态,与更早的状态无关。
数学表示为:P(qt+1=sj∣qt=si,qt−1,…,q1)=P(qt+1=sj∣qt=si)
这个假设简化了状态转移的计算,使得计算量大大降低。
二是,观测独立性假设(Observation Independence Assumption):
这个假设表明,给定当前的隐藏状态,观测值与之前或之后的观测值是相互独立的。
数学表示为:P(Ot=vk∣qt=sj,Ot−1,Ot−2,…,O1)=P(Ot=vk∣qt=sj)
这一假设使得观测序列的概率计算更为简便,只需考虑当前隐藏状态下的观测概率。
如果上面的官话和数学表示看不懂,我给大家翻译成大白话,就是下图:
这两个假设也不难理解,第一个假设就是说隐藏状态只与其前一个隐藏状态相关,与其他无关。第二个假设就是说每个可观测状态都是由它对应的隐藏状态生成的,与其他可观测状态无关。
又是车轱辘话,这不就是矩阵A和矩阵B嘛。矩阵A就是假设1的数学语言,矩阵B就是假设2的数学语言。也所以A矩阵我们叫状态转移概率矩阵。B矩阵叫发射概率矩阵,就是从隐藏状态生成观测结果的过程。矩阵A是因与因之间的关系,矩阵B是每个因与果之间的关系。
(3)从上面的概率题,抽取HMM中的三元组:λ = (π, A, B)
一个隐马尔科夫模型可以用一个三元组:λ=(π,A,B)来表示。其中:π是初始状态分布向量;A是状态转移概率矩阵;B是观测概率矩阵。
还是车轱辘话,三元组里面的π,A,B,前面解释多次了。但是这里要说明的是:我们把(π,A,B)用λ来表示,λ是参数的意思,也就是说π,A,B都是模型的参数。也就是一旦π,A,B定下来后,那HMM概型就确定了。也就是说一组λ=(π,A,B)代表一个HMM。如果π,A,B中的任何一个或多个改变了,那就变成另外一个HMM了。
3、HMM的三个基本问题
隐马尔科夫模型(HMM)涉及三个基本问题:评估问题(Evaluation Problem)、解码问题(Decoding Problem)和学习问题(Learning Problem)。每个问题都有其特定的数学表达方式。
很多人看到这里都会冒充一个疑问,为什么会有这三个问题?!很多资料也不解释就直接堆数学公式,真是云里雾里。这里我解释一下:
前面写的概率题,也就是小标题1,其实就是一个HMM问题。
前面写的小标题2,其实就是一个完整的HMM概型包括的所有东西:观测序列Observations、掩藏序列States、初始状态概率π、隐藏状态转换矩阵A、发射矩阵B。就这五大要素。
这就类似于,我告诉了你"2+3=5",也类似于我告诉了你HMM概型的五要素:
(1)你可以求2+3=?这就是评估问题,有的资料上叫计算问题。我们小标题1的概率题其实就是这个问题,就是计算问题,就是让你计算一下得到“白黑白白黑”这个观测序列的概率。而计算这个问题用的是前向算法或者后向算法。后面我会讲这两个算法。
(2)当你知道了2和5,你可以反推2+?=5,这就是解码问题,有的地方也叫预测问题。就好比我现在知道了观测序列Observations、初始状态概率π、隐藏状态转换矩阵A、发射矩阵B,我反推一下隐藏序列States。反推最大概率的隐藏序列使用的方法是维特比算法(Viterbi Algorithm)。后面也会讲该算法。
这里面还有一层逻辑,就是我们为什么要反推最大概率的隐藏序列?当然是为了预测喽。当你知道了隐藏序列,那是不是就知道了下一个最大概率的隐藏状态-->知道了下一个隐藏状态,是不是就知道了这个隐藏状态对应的最大概率观测值了,是不是就做了预测了?!是不是此时就是一个生成模型了?!
(3)当你知道了答案是5,你推测一下?+ ?=5,这就是学习问题。就是我们试着去学一个最优的(π, A, B),让在这个(π, A, B)下,观测序列Observations的概率最大。这种反推模型参数的任务就是学习问题。但是学习问题又分两种情况:
情况1:我们已知的是观测序列Observations和隐藏序列States的情况下,来反推(π, A, B),此时就是一个有监督的学习任务,使用极大似然估计法来估计参数即可。
情况2:我们只已知观测序列Observations,不知道隐藏序列States,来反推(π, A, B),此时是一个无监督的学习任务,此时得使用EM算法(也称为Baum-Welch算法)来估计参数。
(二)HMM的相关算法
与HMM相关的计算就是上面三大问题的计算。本部分给大家展示上面算法的手动计算过程。
1、前向算法
前向算法就是计算观测序列出现的概率。
我们的小概率题就是这个问题。小概率题就是已知观测序列Observations、初始状态概率π、隐藏状态转换矩阵A、发射矩阵B,求观测序列的概率。
我们先根据概率的定义,用最笨的方法(但是最容易理解呀)手动算一下:
上面的手动计算过程是基于最基本的概率常识来计算的。计算过程和答案肯定都不会错。但是这种计算方式太低效。我们回看这个计算过程,其实这个计算过程就是一个递推的过程,直到序列结束,递推也结束,最后加和所有状态下的概率即可。所以我们看很多资料上的前向算法是这样滴:
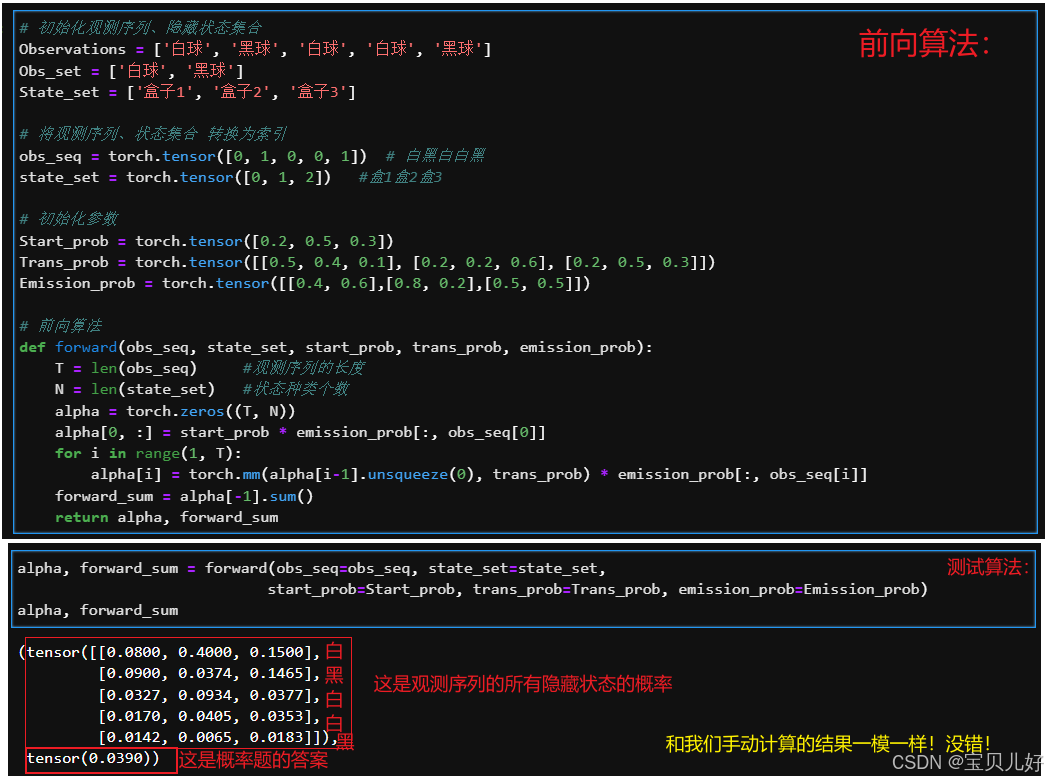
即使看不懂公式,我们也得用代码把算法捋一遍:
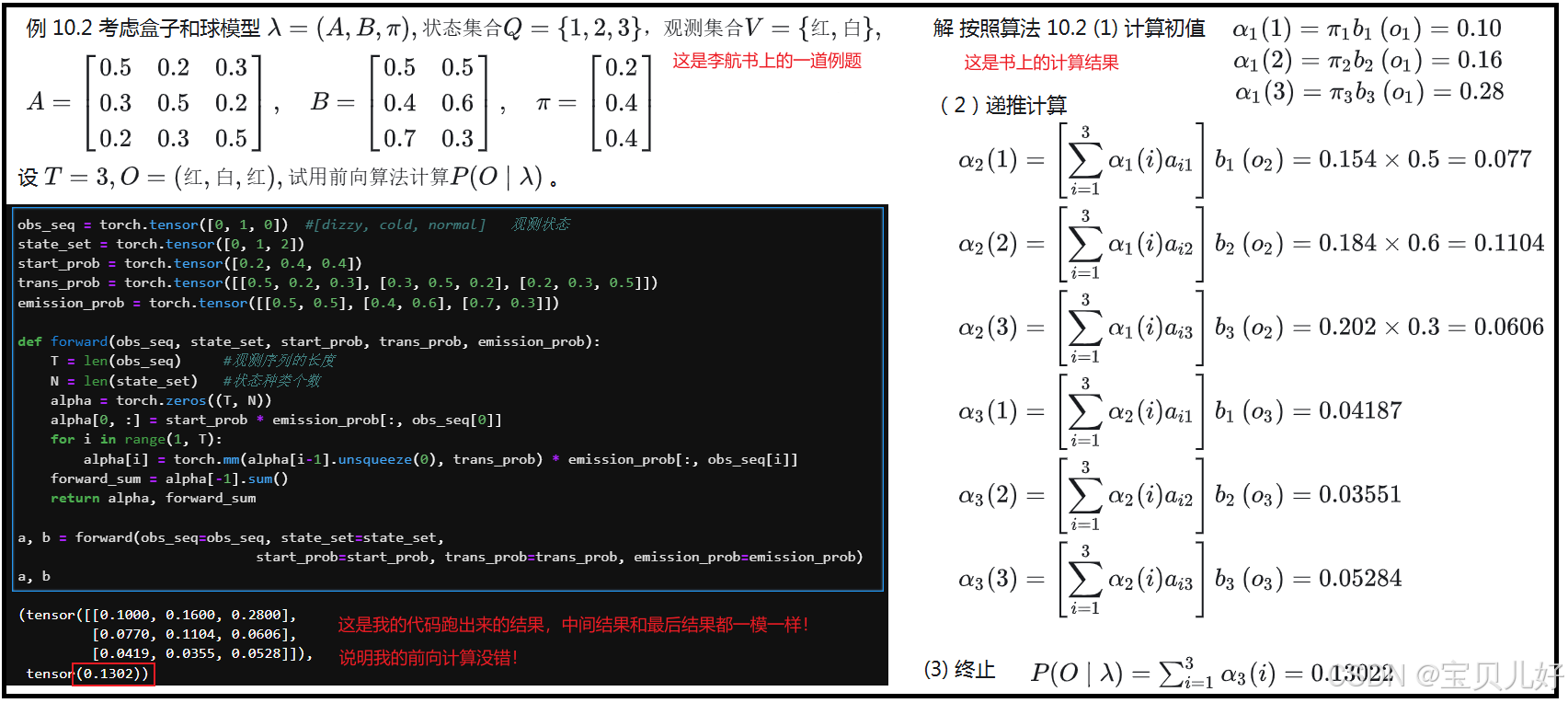
上述代码的计算结果和手动计算的结果是一致的。下面我再拿上面的代码跑一下李航的《统计学习方法》里面的例子,看和书里的计算结果是否一致:
# 初始化观测序列、隐藏状态集合
Observations = ['白球', '黑球', '白球', '白球', '黑球']
Obs_set = ['白球', '黑球']
State_set = ['盒子1', '盒子2', '盒子3']
# 将观测序列、状态集合 转换为索引
obs_seq = torch.tensor([0, 1, 0, 0, 1]) # 白黑白白黑
state_set = torch.tensor([0, 1, 2]) #盒1盒2盒3
# 初始化参数
Start_prob = torch.tensor([0.2, 0.5, 0.3])
Trans_prob = torch.tensor([[0.5, 0.4, 0.1], [0.2, 0.2, 0.6], [0.2, 0.5, 0.3]])
Emission_prob = torch.tensor([[0.4, 0.6],[0.8, 0.2],[0.5, 0.5]])
# 前向算法
def forward(obs_seq, state_set, start_prob, trans_prob, emission_prob):
T = len(obs_seq) #观测序列的长度
N = len(state_set) #状态种类个数
alpha = torch.zeros((T, N))
alpha[0, :] = start_prob * emission_prob[:, obs_seq[0]]
for i in range(1, T):
alpha[i] = torch.mm(alpha[i-1].unsqueeze(0), trans_prob) * emission_prob[:, obs_seq[i]]
forward_sum = alpha[-1].sum()
return alpha, forward_sum
#测试结果
alpha, forward_sum = forward(obs_seq=obs_seq, state_set=state_set,
start_prob=Start_prob, trans_prob=Trans_prob, emission_prob=Emission_prob)
alpha, forward_sum(tensor([[0.0800, 0.4000, 0.1500],
[0.0900, 0.0374, 0.1465],
[0.0327, 0.0934, 0.0377],
[0.0170, 0.0405, 0.0353],
[0.0142, 0.0065, 0.0183]]),
tensor(0.0390))
2、后向算法
后向算法也是计算观测序列出现的概率。后向算法比较难以理解,因为不是常规思路嘛。网上很多资料都是模模糊糊一带而过,对于数学一般的人真是要想很久才能悟出来。我自己也是想了一天,才突然明白的。
但是当我想明白的那一刻,才知道后向算法也是计算序列出现的概率的,当时我的内心是崩溃的,因为前向算法都算出来了,还死磕后向算法干嘛?!吃饱了撑的嘛?!冷静想过以后,只有一个解释:两个算法同时使用可以并行计算,提升效率。假设一个序列有10000个观测值,从前往后一个个算得多费时间呀,正是由于后向算法的发明,我们就可以把这10000个观测值,比如分100个段,就可以并行计算这个100个子序列,效率是不是就大大提升了!所以后向算法还是值得你想破脑袋也要想明白的一个算法。
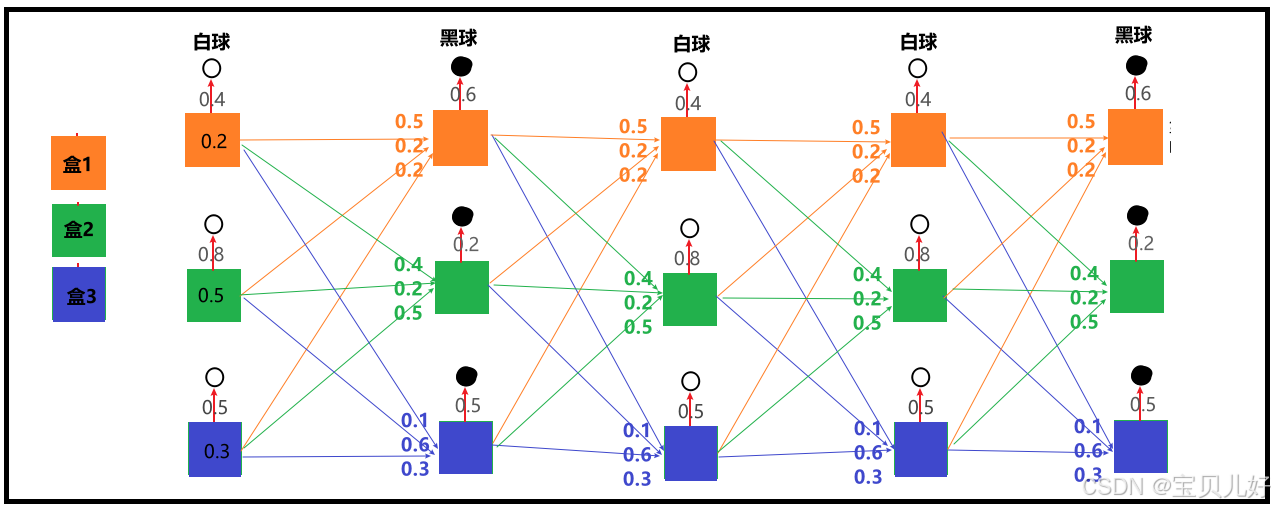
依旧使用我们前向算法用的小案例,下面我把这个小案例中的所有可能路径都画出来:
讲前向算法时,我就没画图,就直接开始手算概率的,那是因为前向计算太好理解了,就是根据状态概率一步步求结果就行。但是此处的后向算法,理解起来有点费劲,它是从结果一步步倒退所有可能的因!这个就比较麻烦,所以我把所有的可能路径都给大家标出来了,这样方便倒着推算。
下面我也先手动计算一下:
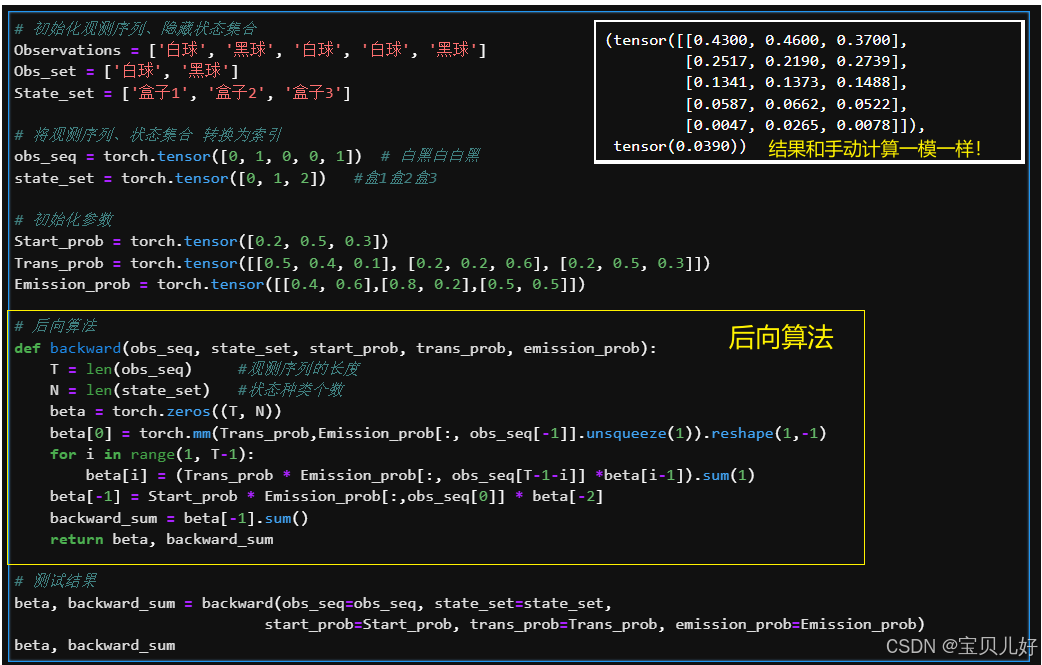
下面开始写后向算法的代码实现:
# 初始化观测序列、隐藏状态集合
Observations = ['白球', '黑球', '白球', '白球', '黑球']
Obs_set = ['白球', '黑球']
State_set = ['盒子1', '盒子2', '盒子3']
# 将观测序列、状态集合 转换为索引
obs_seq = torch.tensor([0, 1, 0, 0, 1]) # 白黑白白黑
state_set = torch.tensor([0, 1, 2]) #盒1盒2盒3
# 初始化参数
Start_prob = torch.tensor([0.2, 0.5, 0.3])
Trans_prob = torch.tensor([[0.5, 0.4, 0.1], [0.2, 0.2, 0.6], [0.2, 0.5, 0.3]])
Emission_prob = torch.tensor([[0.4, 0.6],[0.8, 0.2],[0.5, 0.5]])
# 后向算法
def backward(obs_seq, state_set, start_prob, trans_prob, emission_prob):
T = len(obs_seq) #观测序列的长度
N = len(state_set) #状态种类个数
beta = torch.zeros((T, N))
beta[0] = torch.mm(Trans_prob,Emission_prob[:, obs_seq[-1]].unsqueeze(1)).reshape(1,-1)
for i in range(1, T-1):
beta[i] = (Trans_prob * Emission_prob[:, obs_seq[T-1-i]] *beta[i-1]).sum(1)
beta[-1] = Start_prob * Emission_prob[:,obs_seq[0]] * beta[-2]
backward_sum = beta[-1].sum()
return beta, backward_sum
# 测试结果
beta, backward_sum = backward(obs_seq=obs_seq, state_set=state_set,
start_prob=Start_prob, trans_prob=Trans_prob, emission_prob=Emission_prob)
beta, backward_sum(tensor([[0.4300, 0.4600, 0.3700],
[0.2517, 0.2190, 0.2739],
[0.1341, 0.1373, 0.1488],
[0.0587, 0.0662, 0.0522],
[0.0047, 0.0265, 0.0078]]),
tensor(0.0390))
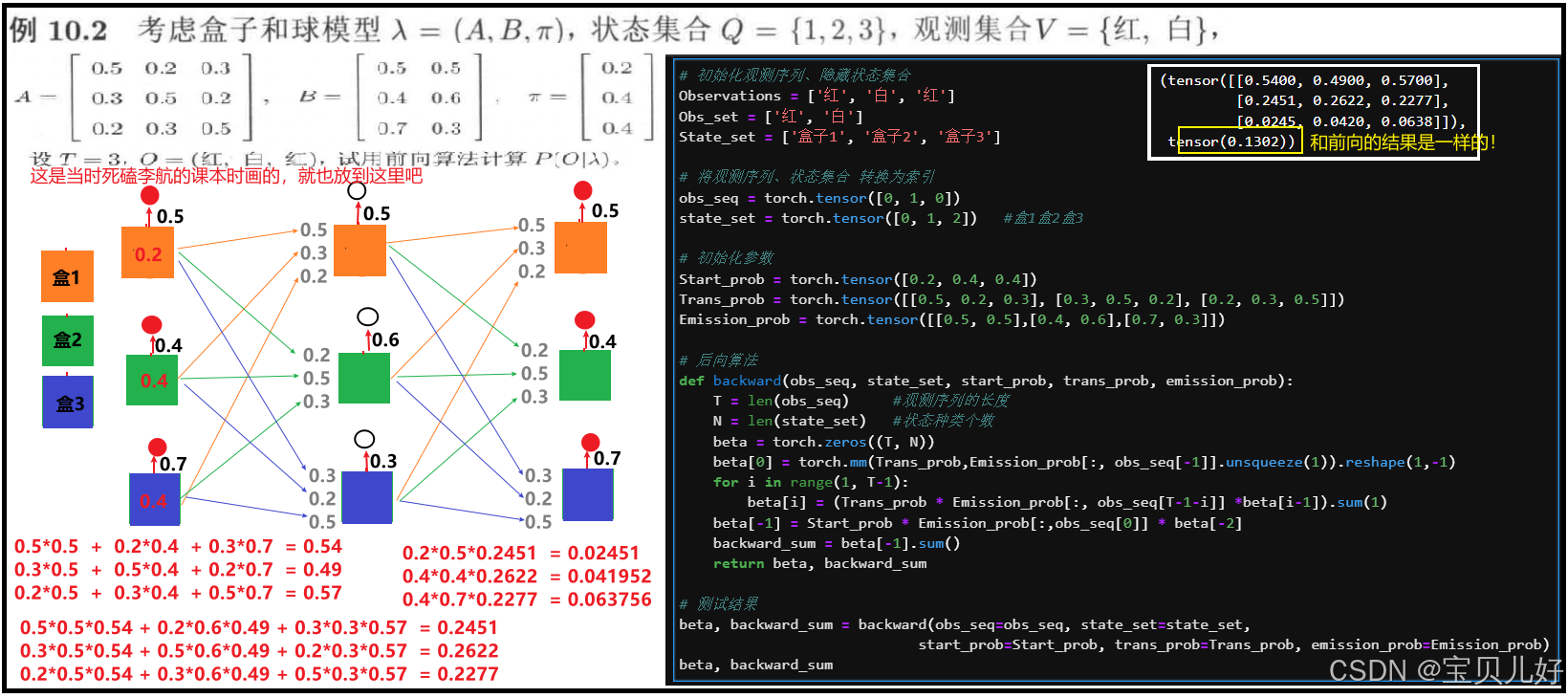
不放心的话,我用这个代码也跑一下李航的那个例子:
网上这篇博文也针对这个例子进行了计算: 【大道至简】机器学习算法之隐马尔科夫模型(Hidden Markov Model, HMM)详解(2)---计算问题:前向算法和后向算法原理详解公式推导及Python实现_pycharm中hmm算法-CSDN博客 ,感兴趣的可以参考,写得非常不错,我一开始也是看这篇博文才得到的启发。
3、维特比算法(Viterbi Algorithm)
待续。。。。。