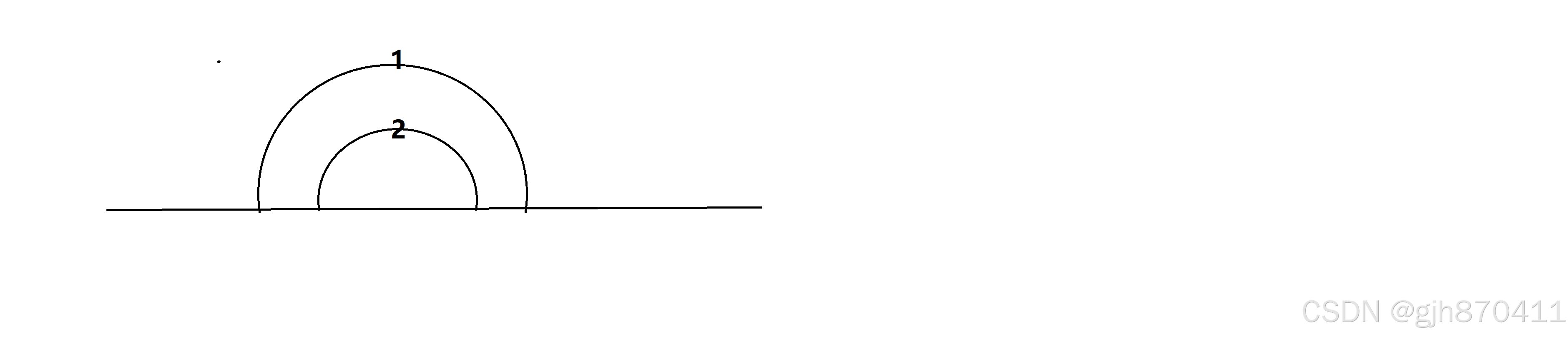题目来自可达鸭 
一 、目录
1.喷水装置(二)
2.加油问题(与CSP-J上的加油问题类似)
3.数列极差问题
二、题解
1.喷水装置(二)
时间限制:1秒 内存限制:128M
题目描述
有一块草坪,横向长w,纵向长为h,在它的橫向中心线上不同位置处装有n(n<=10000)个点状的喷水装置,每个喷水装置i喷水的效果是让以它为中心半径为Ri的圆都被润湿。请在给出的喷水装置中选择尽量少的喷水装置,把整个草坪全部润湿。
输入描述
第一行输入一个正整数N表示共有n次测试数据。每一组测试数据的第一行有三个整数n,w,h,n表示共有n个喷水装置,w表示草坪的横向长度,h表示草坪的纵向长度。随后的n行,都有两个整数xi和ri,xi表示第i个喷水装置的的横坐标(最左边为0),ri表示该喷水装置能覆盖的圆的半径。
输出描述
每组测试数据输出一个正整数,表示共需要多少个喷水装置,每个输出单独占一行。如果不存在一种能够把整个草坪湿润的方案,请输出0。
样例
输入
2 2 8 6 1 1 4 5 2 10 6 4 5 6 5
输出
1 2
题目解析:
首先看这个题,它是一个最优性问题,所以使用贪心去解决。然后判断排序规则,有以下几种排序:
1.L从大到小排
2.l从小到大排
3.r从小到大排
4.r从大到小排
判断包含关系:
判断可知先取1好,所以删除两个:
1.L从大到小排
2.l从小到大排
3.r从小到大排
4.r从大到小排
2、4均可,根据个人习惯来选(我是l从小到大排的)
然后遍历所有的喷水装置,能够覆盖到已覆盖的区域。并且能够覆盖的最远的区域,极为所需区域。(因为要求需要最少的喷水装置)
最后判断一个喷水装置的可覆盖的最大区域。
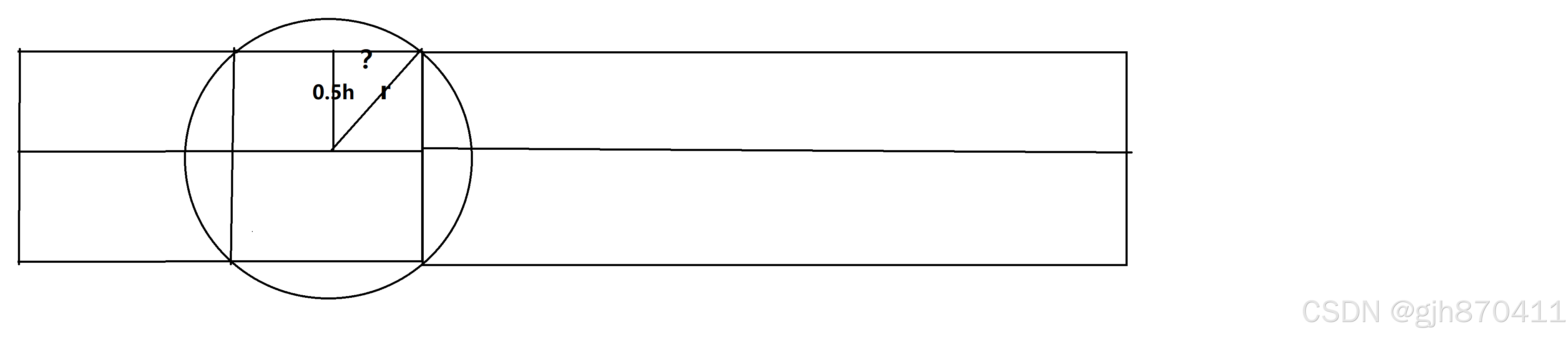
由题意可画图(如下图):
图中?即为所覆盖的面积一半的长。
AC代码如下:
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
struct Node{
double l,r;
}a[10005];
int t,n,w,h;
bool cmp(Node a,Node b){
return a.l<b.l;
}
int main(){
cin>>t;
while(t--){
cin>>n>>w>>h;
double temp=h/2.0;
int x,ri,cnt=0;
for(int i=1;i<=n;i++){
cin>>x>>ri;
if(ri>temp){
double len=sqrt(ri*ri-temp*temp); //求图示?长度
a[++cnt].l=x-len;
a[cnt].r=x+len;
}
}
sort(a+1,a+cnt+1,cmp); //转变成区域覆盖问题,按l从小到大排列
double pos=0,start=1; //遍历的起点,写start为了省时间防止重复计算
int ans=0; //最后结果,相当于cnt
while(pos<w){
double maxx=0; //为了少用喷水装置 ,求取r的最大值
for(int i=start;i<=cnt&&a[i].l<=pos;i++){
maxx=max(maxx,a[i].r);
start=i;
}
if(maxx==0){ //上面没选到
cout<<0<<endl;
break;
}
ans++;
pos=maxx;
if(pos>=w){
cout<<ans<<endl;
break;
}
start++;
}
}
return 0;
}2.加油问题(与CSP-J上的加油问题类似)
题目描述
你需要驾驶一辆卡车行驶L单位的距离。最开始时,卡车上有P单位的汽油。卡车每开1单位距离需要消耗1单位的汽油。
如果在途中车上的汽油耗尽,卡车就无法继续前进,因而无法到达终点。在途中一共有N个加油站。第i个加油站在距离起点Ai单位距离的地方,最多可以给卡车加Bi单位的汽油。假设卡车的燃料箱的容量是无限大的,无论加多少油都没有问题,那么请问卡车是否能到达终点、。如果可以,最少需要加多少次油?如果可以到达终点,输出最少的加油次数,否则输出-1。
限制条件:
1≤N≤10000
1≤L≤1000000,1≤P≤1000000
1≤Ai<L,1≤Bi≤100
输入描述
第一行用三个正整数描述,第一个正整数表示加油站个数,第二个正整数表示行驶距离,第三个正整数表示卡车原有多少汽油。
第二行输入每个加油站距离起点的距离。
第三行输入每个加油站可以给卡车加多少油。
输出描述
输出一行一个整数,表示最少需要加多少次油。
样例
输入
4 25 10 10 14 20 21 10 5 2 4
输出
2
题解:
就是假设有一个神奇的口袋。他能把所有的加油站全部装进去。一旦没有就取出里面油量最高的来加上。如果还是到不了下一个加油站,就取出另外一个最大的油量来,再加上直到到下一个加油站,然后把下一个加油站装到这个口袋里。这个口袋就是优先队列及最大堆最大堆的堆顶。这个堆其实就存的是加油量,它的堆顶就是含油量最高的加油站。因为最后只求数量不求过程,所以说可以利用这个想法去做。此题可以用DP去做,也可以用搜索去做。
AC代码如下:
#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
priority_queue<int> q;
int n,l,p;
struct jyz{
int len;
int num;
}a[10005];
bool cmp(jyz a,jyz b){
return a.len<b.len;
}
int main(){
cin>>n>>l>>p;
for (int i=1;i<=n;i++){
cin>>a[i].len;
}
for (int i=1;i<=n;i++){
cin>>a[i].num;
}
sort(a+1,a+n+1,cmp);
a[++n].len=l;
a[n].num=0;
int pos=0,cnt=0;
for (int i=1;i<=n;i++){
int cha=a[i].len-pos;
while(p<cha){
if (q.size()==0){
cout<<-1;
return 0;
}
else{
cnt++;
p+=q.top();
q.pop();
}
}
pos=a[i].len;
p-=cha;
q.push(a[i].num);
}
cout<<cnt;
return 0;
} 3.数列极差问题
题目描述
在黑板上写了N个正整数组成的一个数列,进行如下操作: 每次擦去其中的两个数a和b,然后在数列中加入一个数a×b+1,如此下去直至黑板上 剩下一个数,在所有按这种操作方式最后得到的数中,最大的为max,最小的为min, 则该数列的极差定义为M=max-min。
请你编程,对于给定的数列,计算极差。
输入描述
输入包含多个测试集。每个测试集的第一个数N表示 正整数序列长度(0<=N<=50000),随后是N个正整数。N为0表示输入结束
输出描述
每个结果一行
样例
输入
3 1 2 3 0
输出
2
题解:
这个题其实很好想利用样例或自拟样例就可以想出来。实际上它的最大值就是把两个最大的去掉。它的最小值就是把两个最小的去掉。然后相减后就能得出正确答案。
AC代码如下:
#include<iostream>
#include<queue>
using namespace std;
priority_queue<int> q;
priority_queue<int> q1;
int n;
int main(){
while (cin>>n){
if (n==0){
break;
}
int t;
for (int i=1;i<=n;i++){
cin>>t;
q.push(t); //max
q1.push(-t); //min
}
while (q.size()>1){
int a,b; //a,b max; c,d min;
a = q.top();
q.pop();
b=q.top();
q.pop();
q.push(a*b+1);
a = q1.top();
q1.pop();
b=q1.top();
q1.pop();
q1.push(-(a*b+1));
}
cout<<-(q.top()-(-q1.top()))<<endl;
q.pop();
q1.pop();
}
return 0;
}