分类算法——逻辑回归详解

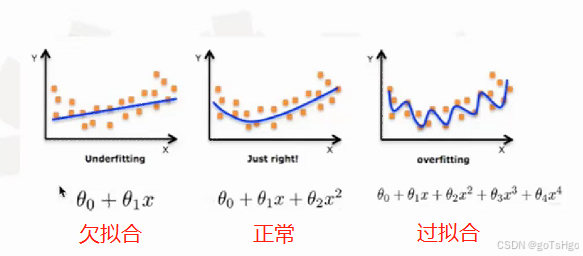
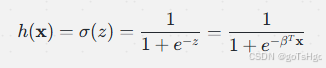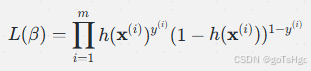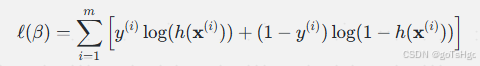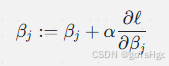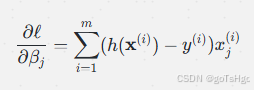逻辑回归（Logistic Regression）是一种广泛使用的分类算法，特别适用于二分类问题。尽管名字中有“回归”二字，逻辑回归实际上是一种分类方法。下面将从底层原理、数学模型、优化方法以及源代码层面详细解析逻辑回归。

1. 基本原理

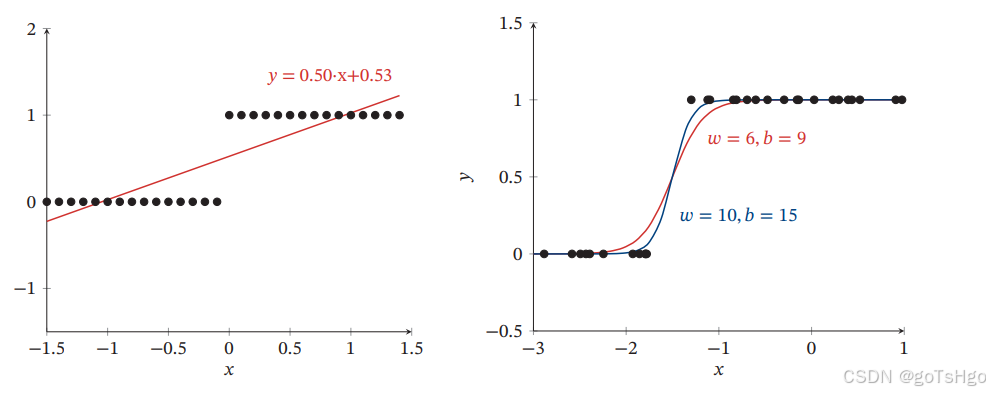
1.1 数学模型

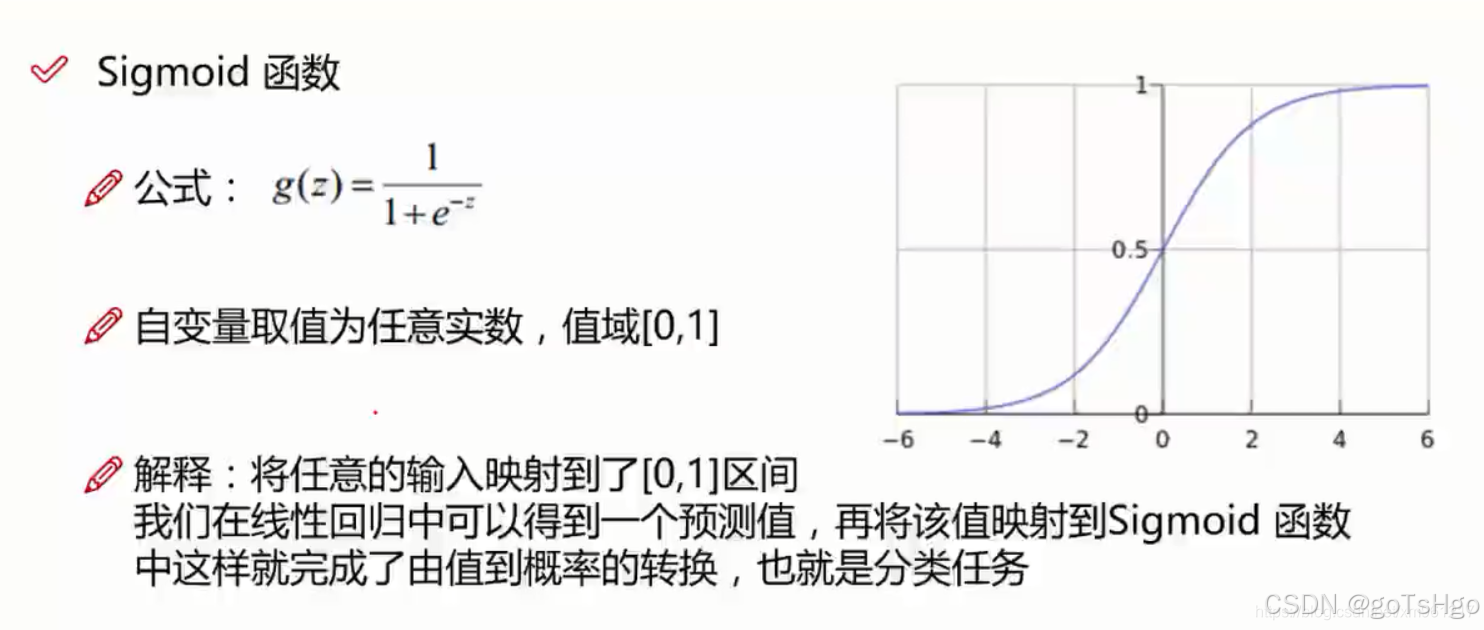
逻辑回归的核心思想是将线性回归的输出通过一个逻辑函数（sigmoid函数）转化为概率值。给定输入特征向量 $x=\left [ x_{1},x_{2}, ... ,x_{n} \right ]$ ，逻辑回归模型可以表示为：

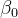
$z=\beta _{0} + \beta _{1}*x_{1} + \beta _{2}*x_{2} + ... + \beta _{n}*x_{n} = + \beta^{T}*x$

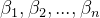
这里， $\beta _{0}$ 是截距项， $\beta _{1} , \beta _{2} ,... ,\beta _{n}$ 是特征对应的权重。

然后通过 sigmoid 函数将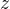转化为概率：

$h(x)= \sigma \left ( z \right ) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\beta ^{\tau }x}}$

其中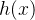， h(x) 表示给定输入特征预测为正类的概率。

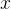
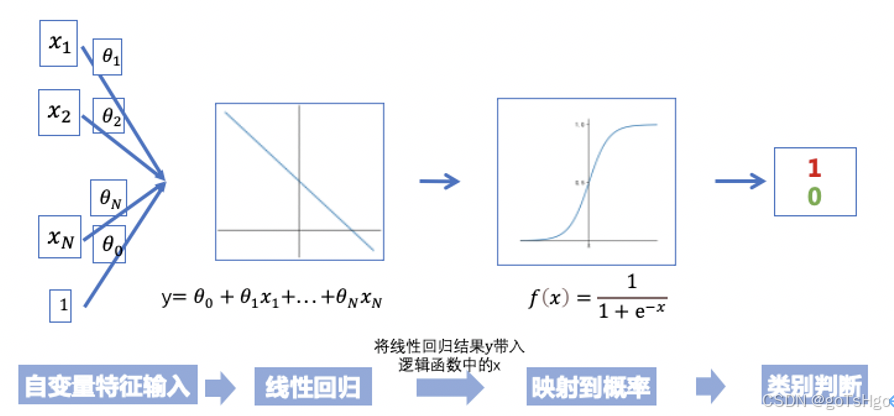
整体的流程

结果类似于：

1.2 目标函数

逻辑回归的目标是最大化似然函数（Likelihood Function），其形式为：

这里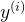， $y^{(i)}$ 是第个样本的标签，是样本数量。通过取对数得到对数似然函数：

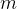
2. 优化方法

为了找到最佳的参数 β，通常使用梯度下降或牛顿法等优化算法来最小化负的对数似然函数。

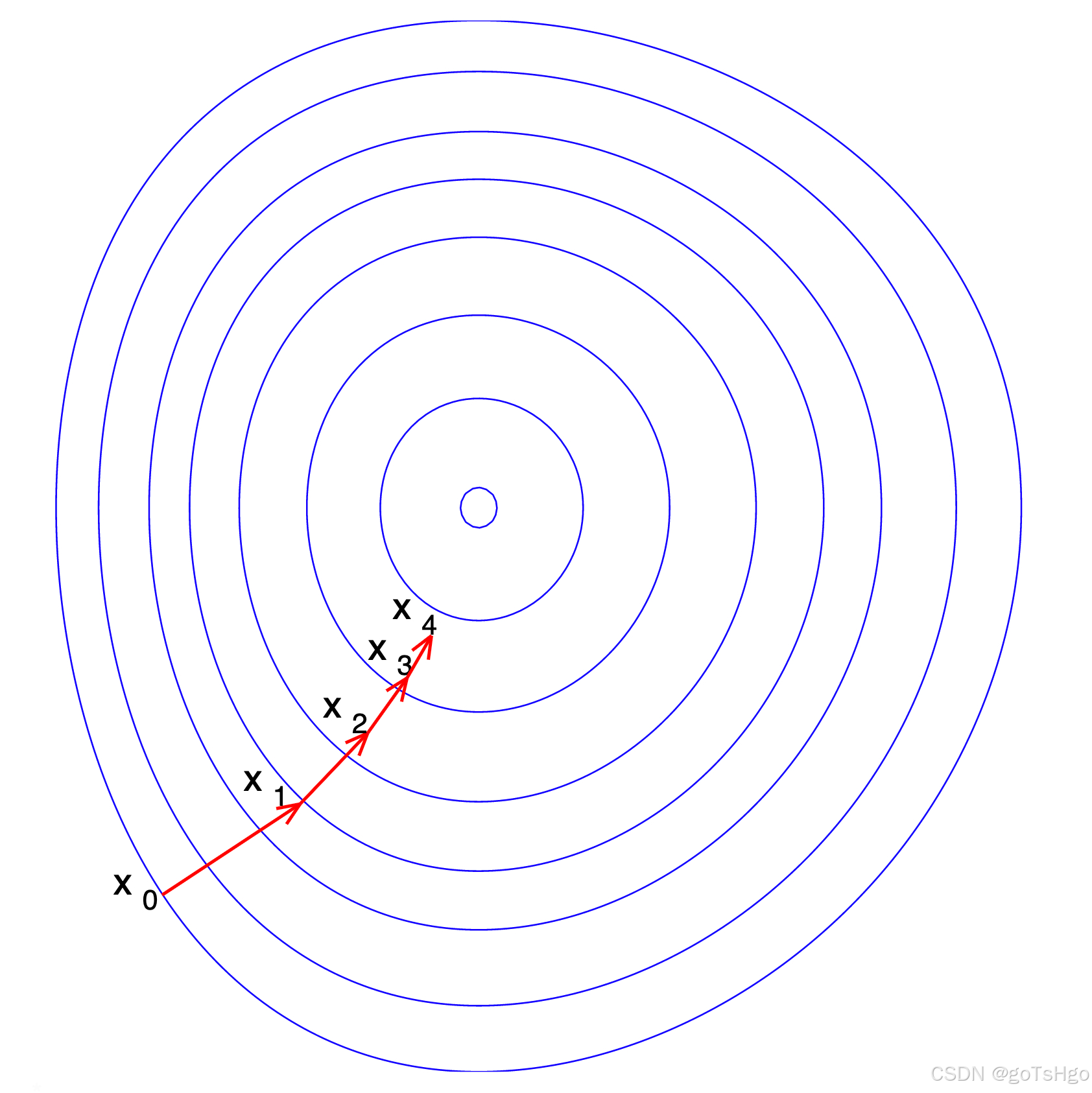
2.1 梯度下降法

更新参数的公式为：

梯度下降例子图示：

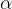
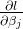
这里， $\alpha$ 是学习率， $\frac{\partial l}{\partial\beta _{j}}$ 是对数似然函数的梯度，可以通过链式法则计算：

2.2 牛顿法

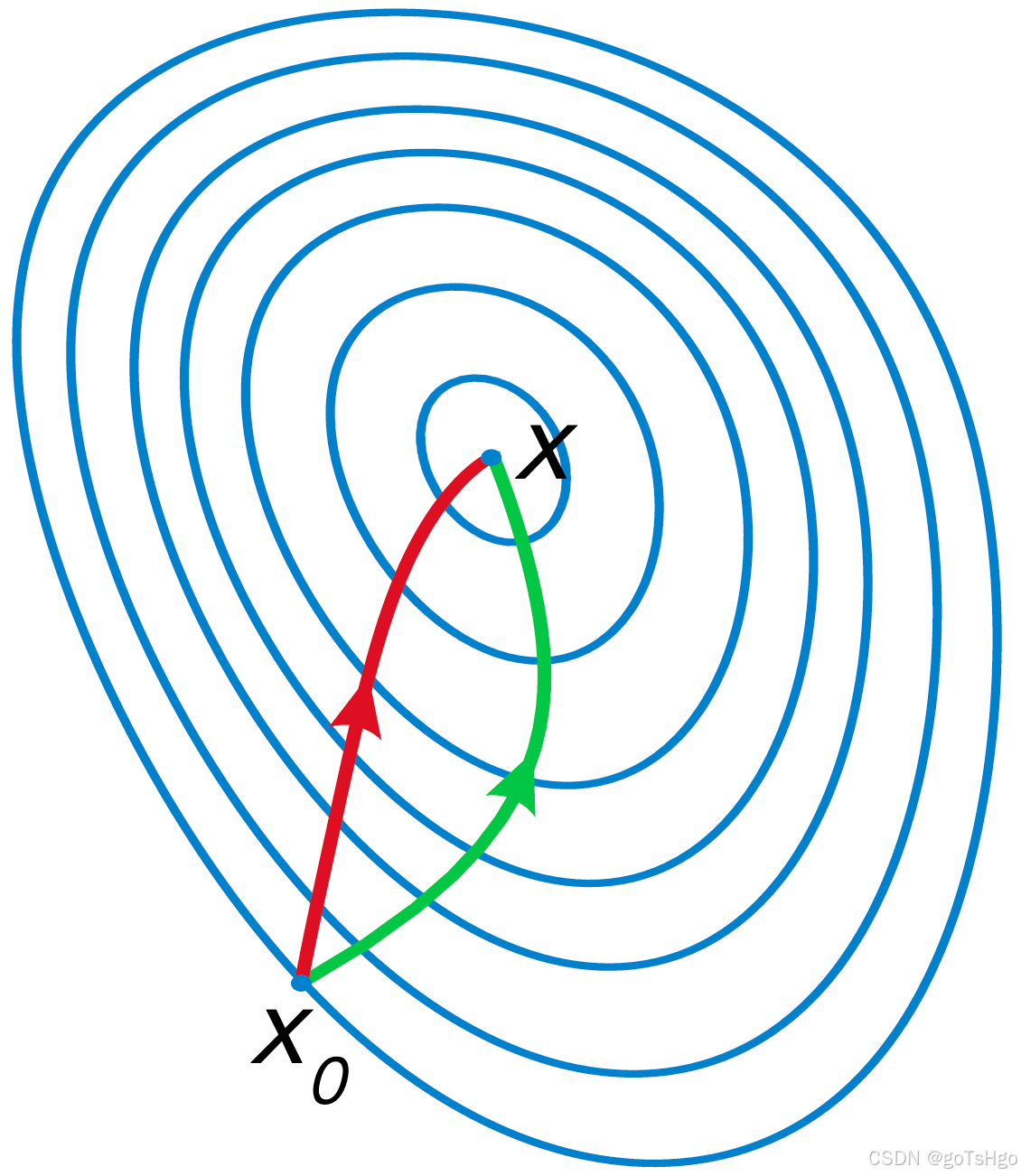
牛顿法利用二阶导数信息（Hessian矩阵）来更快收敛：

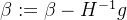
$\beta:=\beta - H^{-1}g$

其中，g 是梯度，H 是 Hessian 矩阵。牛顿法的优势在于收敛速度快，但计算复杂度较高。

绿色为梯度下降，红色为牛顿法，牛顿法的路径更加直接

3. 源代码层面

下面是使用 Python 的 scikit-learn 库实现逻辑回归的示例代码：

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# 加载数据
data = load_iris()
X = data.data
y = (data.target == 0).astype(int)  # 将目标转换为二分类

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建逻辑回归模型
model = LogisticRegression(solver='liblinear')

# 拟合模型
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')

4. 逻辑回归的优缺点

优点

简单易理解：模型结构简单，便于解释和实现。
计算效率高：相比复杂模型，逻辑回归的计算开销较小。
适用性广：可以处理线性可分的二分类问题，且经过适当变换后可应用于多分类问题。

缺点

线性假设：假设特征与输出之间是线性关系，对复杂非线性关系表现不佳。
对异常值敏感：逻辑回归对异常值比较敏感，可能会影响模型性能。
特征独立性假设：逻辑回归假设特征之间是独立的，特征间的相关性可能会影响预测准确性。

总结

逻辑回归是一种强大而有效的分类算法，能够通过概率的方式对输入数据进行建模。其底层原理基于线性模型和逻辑函数的组合，优化过程使用梯度下降等方法来调整模型参数。尽管有其局限性，但在许多实际应用中依然表现优越，尤其在特征数量较少且具有线性可分性的情况下。