梯度反向传播算法推导
- 前言
- 一、单个神经元的计算过程
- 二、每层由单个神经元构成的神经网络
- 三、每层由多个神经元构成的神经网络
- 四、总结
- 每层由单个神经元组成
- 每层由多个神经元组成
- 损失函数对于权重系数和偏置量的影响
- 反向传播
- 参数更新方式
前言
Backward propagation 反向传播算法推导过程
一、单个神经元的计算过程
o u t p u t = σ ( w e i g h t ∗ i n p u t + b i a s ) output=\sigma(weight*input+bias) output=σ(weight∗input+bias)
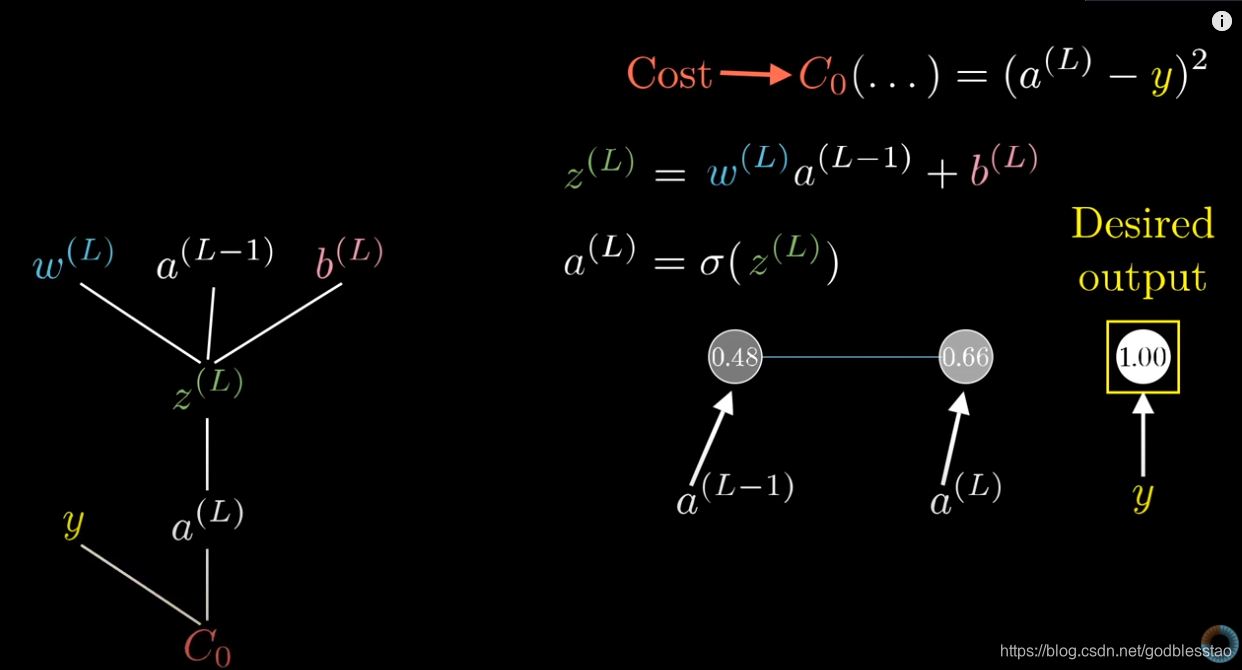
二、每层由单个神经元构成的神经网络
图片来自:https://www.youtube.com/watch?v=tIeHLnjs5U8
出品方:3Blue1Brown
输出神经元的输出值与标签,构成损失函数:
C
o
s
t
=
(
a
L
−
y
)
2
Cost=(a^{L}-y)^2
Cost=(aL−y)2
输出神经元的输出值由上一层的神经元输出值经过激活函数获得:
a
L
=
σ
(
z
L
)
a^{L}=\sigma(z^{L})
aL=σ(zL)
上一层神经元的输出值为:
z
L
=
w
L
∗
a
L
−
1
+
b
L
z^{L}=w^{L}*a^{L-1}+b^{L}
zL=wL∗aL−1+bL
第L层神经元权重系数
w
L
w^{L}
wL,通过影响上一层神经元的输出值
z
L
z^{L}
zL,影响
a
L
a^{L}
aL,进而导致损失函数cost的变化。所以损失函数对第L层神经元权重系数的微分为:
∂
c
o
s
t
∂
w
L
=
∂
z
L
∂
w
L
∂
a
L
∂
z
L
∂
c
o
s
t
∂
a
L
\frac{\partial cost}{\partial w^{L}} = \frac{\partial z^{L}}{\partial w^{L}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial cost}{\partial a^{L}}
∂wL∂cost=∂wL∂zL∂zL∂aL∂aL∂cost
∂
z
L
∂
w
L
=
a
L
−
1
∂
a
L
∂
z
L
=
σ
′
(
z
L
)
∂
c
o
s
t
∂
a
L
=
2
(
a
L
−
y
)
\frac{\partial z^{L}}{\partial w^{L}}=a^{L-1}\\ \frac{\partial a^{L}}{\partial z^{L}}={\sigma}'(z^{L})\\ \frac{\partial cost}{\partial a^{L}}=2(a^{L}-y)\\
∂wL∂zL=aL−1∂zL∂aL=σ′(zL)∂aL∂cost=2(aL−y)
∂
c
o
s
t
∂
w
L
=
a
L
−
1
∗
σ
′
(
z
L
)
∗
2
(
a
L
−
y
)
\frac{\partial cost}{\partial w^{L}} = a^{L-1}* {\sigma}'(z^{L})* 2(a^{L}-y)
∂wL∂cost=aL−1∗σ′(zL)∗2(aL−y)
第L层神经元权重系数
b
L
b^{L}
bL,通过影响上一层神经元的输出值
z
L
z^{L}
zL,影响
a
L
a^{L}
aL,进而导致损失函数cost的变化。
所以损失函数对第L层神经元偏置量的微分为:
∂
c
o
s
t
∂
b
L
=
∂
z
L
∂
b
L
∂
a
L
∂
z
L
∂
c
o
s
t
∂
a
L
\frac{\partial cost}{\partial b^{L}} = \frac{\partial z^{L}}{\partial b^{L}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial cost}{\partial a^{L}}
∂bL∂cost=∂bL∂zL∂zL∂aL∂aL∂cost
∂
z
L
∂
b
L
=
1
∂
a
L
∂
z
L
=
σ
′
(
z
L
)
∂
c
o
s
t
∂
a
L
=
2
(
a
L
−
y
)
\frac{\partial z^{L}}{\partial b^{L}}=1\\ \frac{\partial a^{L}}{\partial z^{L}}={\sigma}'(z^{L})\\ \frac{\partial cost}{\partial a^{L}}=2(a^{L}-y)\\
∂bL∂zL=1∂zL∂aL=σ′(zL)∂aL∂cost=2(aL−y)
∂
c
o
s
t
∂
b
L
=
σ
′
(
z
L
)
∗
2
(
a
L
−
y
)
\frac{\partial cost}{\partial b^{L}} = {\sigma}'(z^{L})* 2(a^{L}-y)
∂bL∂cost=σ′(zL)∗2(aL−y)
第L层对其权重的微分为:
∂
a
L
∂
w
L
=
a
L
−
1
∗
σ
′
(
z
L
)
\frac{\partial a^{L}}{\partial w^{L}} = a^{L-1}* {\sigma}'(z^{L})
∂wL∂aL=aL−1∗σ′(zL)
第L层对其偏置量的微分为:
∂
a
L
∂
b
L
=
σ
′
(
z
L
)
\frac{\partial a^{L}}{\partial b^{L}} = {\sigma}'(z^{L})
∂bL∂aL=σ′(zL)
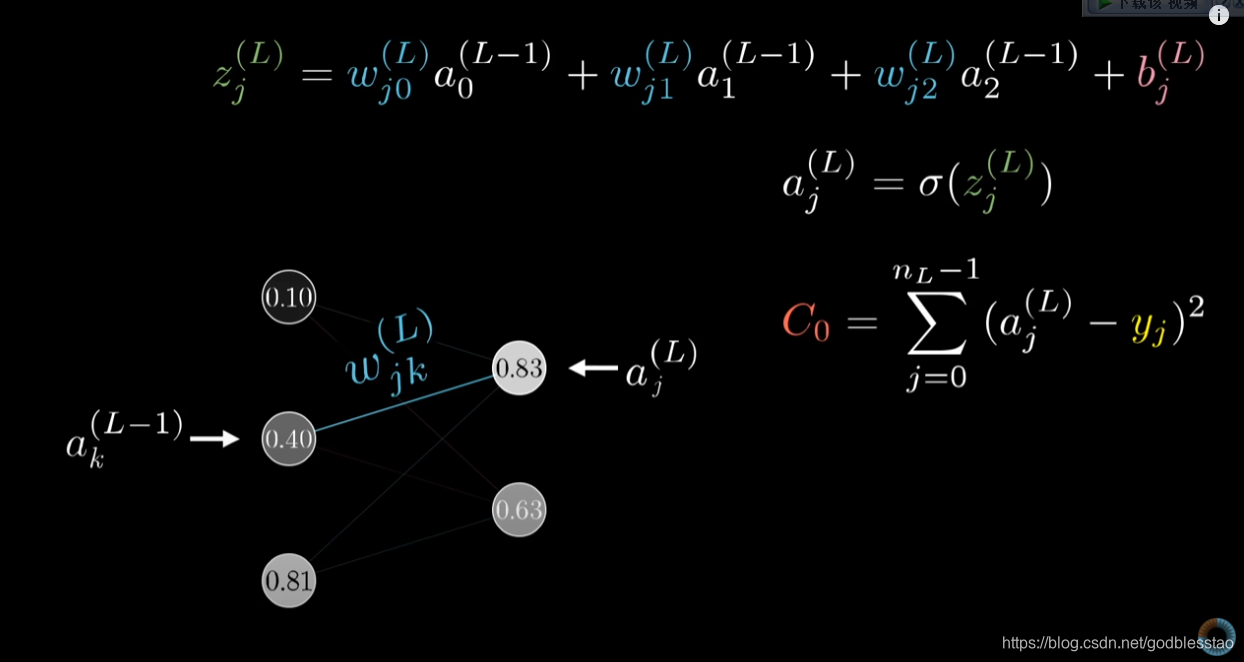
三、每层由多个神经元构成的神经网络
图片来自:https://www.youtube.com/watch?v=tIeHLnjs5U8
出品方:3Blue1Brown
第L层的神经元
a
j
L
a^{L}_{j}
ajL与第L-1层的神经元
a
k
L
−
1
a^{L-1}_{k}
akL−1,之间的权重系数为
w
j
k
L
w^{L}_{jk}
wjkL,第L层的神经元
a
j
L
a^{L}_{j}
ajL的偏置量为
b
j
L
b^{L}_{j}
bjL。
C
0
=
∑
j
=
0
n
L
−
1
(
a
j
L
−
y
j
)
2
C_{0}=\sum_{j=0}^{n^{L}-1}(a^{L}_{j}-y_{j})^2
C0=j=0∑nL−1(ajL−yj)2
其中:
z
j
L
=
∑
k
=
0
n
L
−
1
−
1
a
k
L
−
1
w
j
k
L
+
b
j
L
a
j
L
=
σ
(
z
j
L
)
z^{L}_{j}=\sum_{k=0}^{n^{L-1}-1}a^{L-1}_{k}w^{L}_{jk}+b^{L}_{j} \\ a^{L}_{j}=\sigma(z^{L}_{j})
zjL=k=0∑nL−1−1akL−1wjkL+bjLajL=σ(zjL)
所以损失函数
C
0
C_{0}
C0对
w
j
k
L
w^{L}_{jk}
wjkL的微分为:
∂
C
0
∂
w
j
k
L
=
∂
z
j
L
∂
w
j
k
L
∂
a
j
L
∂
z
j
L
∂
C
0
∂
a
j
L
\frac { \partial C_0}{\partial w^{L}_{jk}} = \frac{\partial z^{L}_{j}}{\partial w^{L}_{jk}} \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}} \frac{\partial C_{0}}{\partial a^{L}_{j}}
∂wjkL∂C0=∂wjkL∂zjL∂zjL∂ajL∂ajL∂C0
∂
z
j
L
∂
w
j
k
L
=
a
k
L
−
1
∂
a
j
L
∂
z
j
L
=
σ
′
(
z
L
)
∂
C
0
∂
a
j
L
=
2
(
a
j
L
−
y
j
)
\frac{\partial z^{L}_{j}}{\partial w^{L}_{jk}}=a^{L-1}_{k}\\ \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}}={\sigma}'(z^{L})\\ \frac{\partial C_{0}}{\partial a^{L}_{j}}=2(a^{L}_{j}-y_{j})
∂wjkL∂zjL=akL−1∂zjL∂ajL=σ′(zL)∂ajL∂C0=2(ajL−yj)
∂
C
0
∂
w
j
k
L
=
a
k
L
−
1
∗
σ
′
(
z
L
)
∗
2
(
a
j
L
−
y
j
)
\frac { \partial C_0}{\partial w^{L}_{jk}} =a^{L-1}_{k}*{\sigma}'(z^{L})*2(a^{L}_{j}-y_{j})
∂wjkL∂C0=akL−1∗σ′(zL)∗2(ajL−yj)
所以损失函数
C
0
C_{0}
C0对
b
j
L
b^{L}_{j}
bjL的微分为:
∂
C
0
∂
b
j
L
=
∂
z
j
L
∂
b
j
L
∂
a
j
L
∂
z
j
L
∂
C
0
∂
a
j
L
\frac { \partial C_0}{\partial b^{L}_{j}} = \frac{\partial z^{L}_{j}}{\partial b^{L}_{j}} \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}} \frac{\partial C_{0}}{\partial a^{L}_{j}}
∂bjL∂C0=∂bjL∂zjL∂zjL∂ajL∂ajL∂C0
∂
z
j
L
∂
b
j
L
=
1
∂
a
j
L
∂
z
j
L
=
σ
′
(
z
L
)
∂
C
0
∂
a
j
L
=
2
(
a
j
L
−
y
j
)
\frac{\partial z^{L}_{j}}{\partial b^{L}_{j}}=1\\ \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}}={\sigma}'(z^{L})\\ \frac{\partial C_{0}}{\partial a^{L}_{j}}=2(a^{L}_{j}-y_{j})
∂bjL∂zjL=1∂zjL∂ajL=σ′(zL)∂ajL∂C0=2(ajL−yj)
∂
C
0
∂
w
j
k
L
=
σ
′
(
z
L
)
∗
2
(
a
j
L
−
y
j
)
\frac { \partial C_0}{\partial w^{L}_{jk}} ={\sigma}'(z^{L})*2(a^{L}_{j}-y_{j})
∂wjkL∂C0=σ′(zL)∗2(ajL−yj)
第L层的神经元
a
j
L
a^{L}_{j}
ajL对其权重
w
j
k
L
w^{L}_{jk}
wjkL的微分为:
∂
a
j
L
∂
w
j
k
L
=
∂
z
j
L
∂
w
j
k
L
∂
a
j
L
∂
z
j
L
=
a
k
L
−
1
∗
σ
′
(
z
L
)
\frac { \partial a^{L}_{j}}{\partial w^{L}_{jk}}= \frac{\partial z^{L}_{j}}{\partial w^{L}_{jk}} \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}} =a^{L-1}_{k}*{\sigma}'(z^{L})
∂wjkL∂ajL=∂wjkL∂zjL∂zjL∂ajL=akL−1∗σ′(zL)
第L层的神经元
a
j
L
a^{L}_{j}
ajL对其权重
b
j
L
b^{L}_{j}
bjL的微分为:
∂
a
j
L
∂
b
j
L
=
∂
z
j
L
∂
b
j
L
∂
a
j
L
∂
z
j
L
=
σ
′
(
z
L
)
\frac { \partial a^{L}_{j}}{\partial b^{L}_{j}}= \frac{\partial z^{L}_{j}}{\partial b^{L}_{j}} \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}} ={\sigma}'(z^{L})
∂bjL∂ajL=∂bjL∂zjL∂zjL∂ajL=σ′(zL)
四、总结
每层由单个神经元组成
对于每层只有一个神经元,共有L层的神经网络。
经过初始化参数,完成前向计算过程,
w
L
−
1
w^{L-1}
wL−1、
a
L
−
1
a^{L-1}
aL−1、
a
L
−
2
a^{L-2}
aL−2为已知的。
损失函数对于第
L
L
L层的权重系数
w
L
w^{L}
wL以及偏置量
b
L
b^{L}
bL的微分为:
∂
C
0
∂
w
L
=
∂
C
0
∂
a
L
∂
a
L
∂
z
L
∂
z
L
∂
w
L
=
C
0
′
(
a
L
)
∗
σ
′
(
z
L
)
∗
a
L
−
1
∂
C
0
∂
b
L
=
∂
C
0
∂
a
L
∂
a
L
∂
z
L
∂
z
L
∂
b
L
=
C
0
′
(
a
L
)
∗
σ
′
(
z
L
)
\begin{aligned} \frac{\partial C_{0}}{\partial w^{L}} &= \frac{\partial C_{0}}{\partial a^{L}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial z^{L}}{\partial w^{L}} ={C_0}'(a^{L})*{\sigma}'(z^{L})*a^{L-1}\\ \frac{\partial C_{0}}{\partial b^{L}} &= \frac{\partial C_{0}}{\partial a^{L}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial z^{L}}{\partial b^{L}}= {C_0}'(a^{L})*{\sigma}'(z^{L}) \end{aligned}
∂wL∂C0∂bL∂C0=∂aL∂C0∂zL∂aL∂wL∂zL=C0′(aL)∗σ′(zL)∗aL−1=∂aL∂C0∂zL∂aL∂bL∂zL=C0′(aL)∗σ′(zL)
损失函数对于第
L
−
1
L-1
L−1层的权重系数
w
L
−
1
w^{L-1}
wL−1以及偏置量
b
L
−
1
b^{L-1}
bL−1的微分为:
∂
C
0
∂
w
L
−
1
=
∂
C
0
∂
a
L
∂
a
L
∂
z
L
∂
z
L
∂
a
L
−
1
∂
a
L
−
1
∂
z
L
−
1
∂
z
L
−
1
∂
w
L
−
1
=
C
0
′
(
a
L
)
∗
σ
′
(
z
L
)
∗
w
L
∗
σ
′
(
z
L
−
1
)
∗
a
L
−
2
∂
C
0
∂
b
L
−
1
=
∂
C
0
∂
a
L
∂
a
L
∂
z
L
∂
z
L
∂
a
L
−
1
∂
a
L
−
1
∂
z
L
−
1
∂
z
L
−
1
∂
b
L
−
1
=
C
0
′
(
a
L
)
∗
σ
′
(
z
L
)
∗
w
L
∗
σ
′
(
z
L
−
1
)
\begin{aligned} \frac{\partial C_{0}}{\partial w^{L-1}}&= \frac{\partial C_{0}}{\partial a^{L}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial z^{L}}{\partial a^{L-1}} \frac{\partial a^{L-1}}{\partial z^{L-1}} \frac{\partial z^{L-1}}{\partial w^{L-1}}= {C_0}'(a^{L})*{\sigma}'(z^{L})*w^{L}*{\sigma}'(z^{L-1})*a^{L-2}\\ \frac{\partial C_{0}}{\partial b^{L-1}}&= \frac{\partial C_{0}}{\partial a^{L}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial z^{L}}{\partial a^{L-1}} \frac{\partial a^{L-1}}{\partial z^{L-1}} \frac{\partial z^{L-1}}{\partial b^{L-1}}= {C_0}'(a^{L})*{\sigma}'(z^{L})*w^{L}*{\sigma}'(z^{L-1}) \end{aligned}
∂wL−1∂C0∂bL−1∂C0=∂aL∂C0∂zL∂aL∂aL−1∂zL∂zL−1∂aL−1∂wL−1∂zL−1=C0′(aL)∗σ′(zL)∗wL∗σ′(zL−1)∗aL−2=∂aL∂C0∂zL∂aL∂aL−1∂zL∂zL−1∂aL−1∂bL−1∂zL−1=C0′(aL)∗σ′(zL)∗wL∗σ′(zL−1)
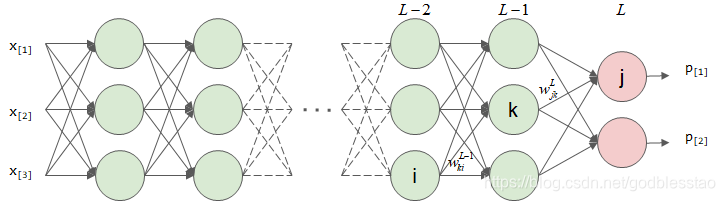
每层由多个神经元组成
对于一个全连接深度神经网络,假设其有L层,包含了输入层、隐含层和输出层,
损失函数对第
L
L
L层,第
j
j
j个神经元
a
j
L
a^{L}_{j}
ajL,第
k
k
k个权重
w
j
k
L
w^{L}_{jk}
wjkL以及偏置量
b
j
L
b^{L}_{j}
bjL的微分为:
∂
C
0
∂
w
j
k
L
=
∂
C
0
∂
a
j
L
∂
a
j
L
∂
z
j
L
∂
z
j
L
∂
w
j
k
L
=
C
0
′
(
a
j
L
)
∗
σ
′
(
z
j
L
)
∗
a
k
L
−
1
∂
C
0
∂
b
j
L
=
∂
C
0
∂
a
j
L
∂
a
j
L
∂
z
j
L
∂
z
j
L
∂
b
j
L
=
C
0
′
(
a
j
L
)
∗
σ
′
(
z
j
L
)
\begin{aligned} \frac { \partial C_0}{\partial w^{L}_{jk}} &= \frac{\partial C_{0}}{\partial a^{L}_{j}} \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}} \frac{\partial z^{L}_{j}}{\partial w^{L}_{jk}}= {C_0}'(a^{L}_{j})*{\sigma}'(z^{L}_{j})*a^{L-1}_{k}\\ \frac { \partial C_0}{\partial b^{L}_{j}} &= \frac{\partial C_{0}}{\partial a^{L}_{j}} \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}} \frac{\partial z^{L}_{j}}{\partial b^{L}_{j}}= {C_0}'(a^{L}_{j})*{\sigma}'(z^{L}_{j}) \end{aligned}
∂wjkL∂C0∂bjL∂C0=∂ajL∂C0∂zjL∂ajL∂wjkL∂zjL=C0′(ajL)∗σ′(zjL)∗akL−1=∂ajL∂C0∂zjL∂ajL∂bjL∂zjL=C0′(ajL)∗σ′(zjL)
损失函数对第
L
−
1
L-1
L−1,第
k
k
k个神经元
a
k
L
−
1
a^{L-1}_{k}
akL−1,第
i
i
i个权重
w
k
i
L
−
1
w^{L-1}_{ki}
wkiL−1以及偏置量
b
k
L
−
1
b^{L-1}_{k}
bkL−1的微分为:
∂
C
0
∂
w
k
i
L
−
1
=
∑
j
=
0
n
L
−
1
(
∂
C
0
∂
a
j
L
∂
a
j
L
∂
z
j
L
∂
z
j
L
∂
a
k
L
−
1
∂
a
k
L
−
1
∂
z
k
L
−
1
∂
z
k
L
−
1
∂
w
k
i
L
−
1
)
=
∑
j
=
0
n
L
−
1
(
C
0
′
(
a
j
L
)
∗
σ
′
(
z
j
L
)
∗
w
j
k
L
∗
σ
′
(
z
k
L
−
1
)
∗
a
i
L
−
2
)
∂
C
0
∂
b
k
L
−
1
=
∑
j
=
0
n
L
−
1
(
∂
C
0
∂
a
j
L
∂
a
j
L
∂
z
j
L
∂
z
j
L
∂
a
k
L
−
1
∂
a
k
L
−
1
∂
z
k
L
−
1
∂
z
k
L
−
1
∂
b
k
L
−
1
)
=
∑
j
=
0
n
L
−
1
(
C
0
′
(
a
j
L
)
∗
σ
′
(
z
j
L
)
∗
w
j
k
L
∗
σ
′
(
z
k
L
−
1
)
)
\begin{aligned} \frac { \partial C_0}{\partial w^{L-1}_{ki}}&= \sum_{j=0}^{n^L-1}( \frac{\partial C_{0}}{\partial a^{L}_{j}} \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}} \frac{\partial z^{L}_{j}}{\partial a^{L-1}_{k}} \frac{\partial a^{L-1}_{k}}{\partial z^{L-1}_{k}} \frac{\partial z^{L-1}_{k}}{\partial w^{L-1}_{ki}} )= \sum_{j=0}^{n^L-1}( {C_0}'(a^{L}_{j})*{\sigma}'(z^{L}_{j})*w^{L}_{jk}*{\sigma}'(z^{L-1}_{k})*a^{L-2}_{i} )\\ \frac { \partial C_0}{\partial b^{L-1}_{k}}&= \sum_{j=0}^{n^L-1}( \frac{\partial C_{0}}{\partial a^{L}_{j}} \frac{\partial a^{L}_{j}}{\partial z^{L}_{j}} \frac{\partial z^{L}_{j}}{\partial a^{L-1}_{k}} \frac{\partial a^{L-1}_{k}}{\partial z^{L-1}_{k}} \frac{\partial z^{L-1}_{k}}{\partial b^{L-1}_{k}} )= \sum_{j=0}^{n^L-1}( {C_0}'(a^{L}_{j})*{\sigma}'(z^{L}_{j})*w^{L}_{jk}*{\sigma}'(z^{L-1}_{k}) ) \end{aligned}
∂wkiL−1∂C0∂bkL−1∂C0=j=0∑nL−1(∂ajL∂C0∂zjL∂ajL∂akL−1∂zjL∂zkL−1∂akL−1∂wkiL−1∂zkL−1)=j=0∑nL−1(C0′(ajL)∗σ′(zjL)∗wjkL∗σ′(zkL−1)∗aiL−2)=j=0∑nL−1(∂ajL∂C0∂zjL∂ajL∂akL−1∂zjL∂zkL−1∂akL−1∂bkL−1∂zkL−1)=j=0∑nL−1(C0′(ajL)∗σ′(zjL)∗wjkL∗σ′(zkL−1))
损失函数对于权重系数和偏置量的影响
某个权重对损失函数的影响,与这个权重连接的前一层神经元经过激活函数的输出有关,与这个权重连接的本层神经元与损失函数所有连接有关。可以分为2方面:
1.前一层神经元输出的影响;
2.当前层及其连接到损失函数的所有连接路径上的激活函数倒数以及权重系数.
某个偏置量对损失函数的影响,这个偏置量连接的本层神经元与损失函数所有连接有关。
另一方面也可以看出,激活函数微分操作的难易,会直接影响到所有参数梯度的计算难度。
反向传播
首先经过构建神经网络架构,通过参数初始化使所有神经元的权重和偏置量具有一个初始值,通过前向计算,获得所有神经元的输出值。
然后由输出层依次向输入层,逐层计算每层参数的梯度信息。此为梯度的反向传播(backward propagation)。
参数更新方式
参数更新方式就是大名鼎鼎的梯度下降(gradient descent)算法啦。
w
n
e
w
=
w
n
o
w
−
l
r
∗
∂
C
0
∂
w
w_{new}=w_{now}-lr*\frac{\partial C_{0}}{\partial w}
wnew=wnow−lr∗∂w∂C0