全排列问题

leetCode 46

使用回溯法解决 —— 解法1

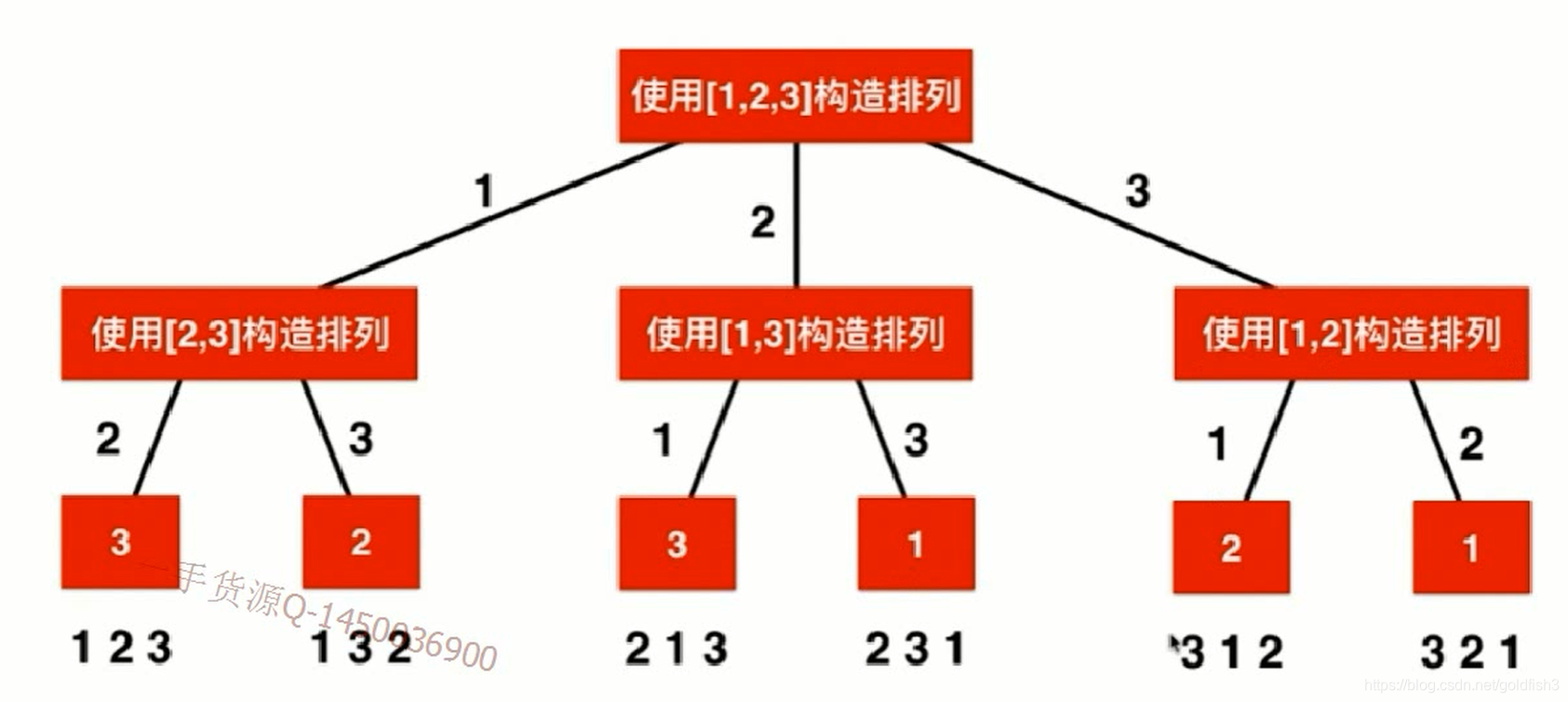
如图：全排列问题是一个典型的树型问题：

import java.util.*;

public class Main {
    private List<List<Integer>> res = new ArrayList<List<Integer>>();
    private boolean[] flag;
    public static void main(String[] args) {
        Main main = new Main();
        int[] nums = {1,2,3};
        List<List<Integer>> res = main.permute(nums);
        for (List<Integer> l:res){
            for (Integer i:l){
                System.out.print(i);
            }
            System.out.println();
        }
    }

    public void premuteCore(int[] nums,ArrayList<Integer> tmp,int index){
        if (index == nums.length){
            ArrayList<Integer> res = new ArrayList<Integer>();
            for (Integer e : tmp){
                res.add(e);
            }
            this.res.add(res);
            return;
        }

        for (int i=0; i<nums.length; i++){
            if (flag[i] != true){
                tmp.add(nums[i]);
                flag[i] = true;
                premuteCore(nums,tmp,index+1);
                tmp.remove(tmp.size()-1);
                flag[i] = false;
            }
        }
    }

    public List<List<Integer>> permute(int[] nums) {
        flag = new boolean[nums.length];
        premuteCore(nums, new ArrayList<Integer>(),0);
        return  res;
    }
}

使用回溯法解决 —— 解法2

本质：任何一个组合都可以通过字符串的两两交换得到，这意味着，可以通过遍历所有的两两交换得到所有排列
这种解法比上面的解法效率高，缺点在于只能求全排列，不能求n个中取m个的排列情况
将第一个元素和后面的逐个交换，然后再第一个元素交换的基础上，将第二个元素和后面的逐个交换

import java.util.*;

public class Main {
    private List<List<Integer>> res = new ArrayList<List<Integer>>();

    public static void main(String[] args) {
        Main main = new Main();
        int[] nums = {1,2,3};
        List<List<Integer>> res = main.permute(nums);
        for (List<Integer> l:res){
            for (Integer i:l){
                System.out.print(i);
            }
            System.out.println();
        }
    }

    public void premuteCore(int[] nums,int index){
        if (index == nums.length-1){
            ArrayList<Integer> res = new ArrayList<Integer>();
            for (int i=0; i<nums.length; i++)
                res.add(nums[i]);
            this.res.add(res);
            return;
        }

        for (int i=index; i<nums.length; i++){
            if (i != index){
                int tmp = nums[index];
                nums[index] = nums[i];
                nums[i] = tmp;
            }
            premuteCore(nums,index+1);
            if (i != index){
                int tmp = nums[index];
                nums[index] = nums[i];
                nums[i] = tmp;
            }
        }
    }

    public List<List<Integer>> permute(int[] nums) {
        premuteCore(nums,0);
        return  res;
    }
}

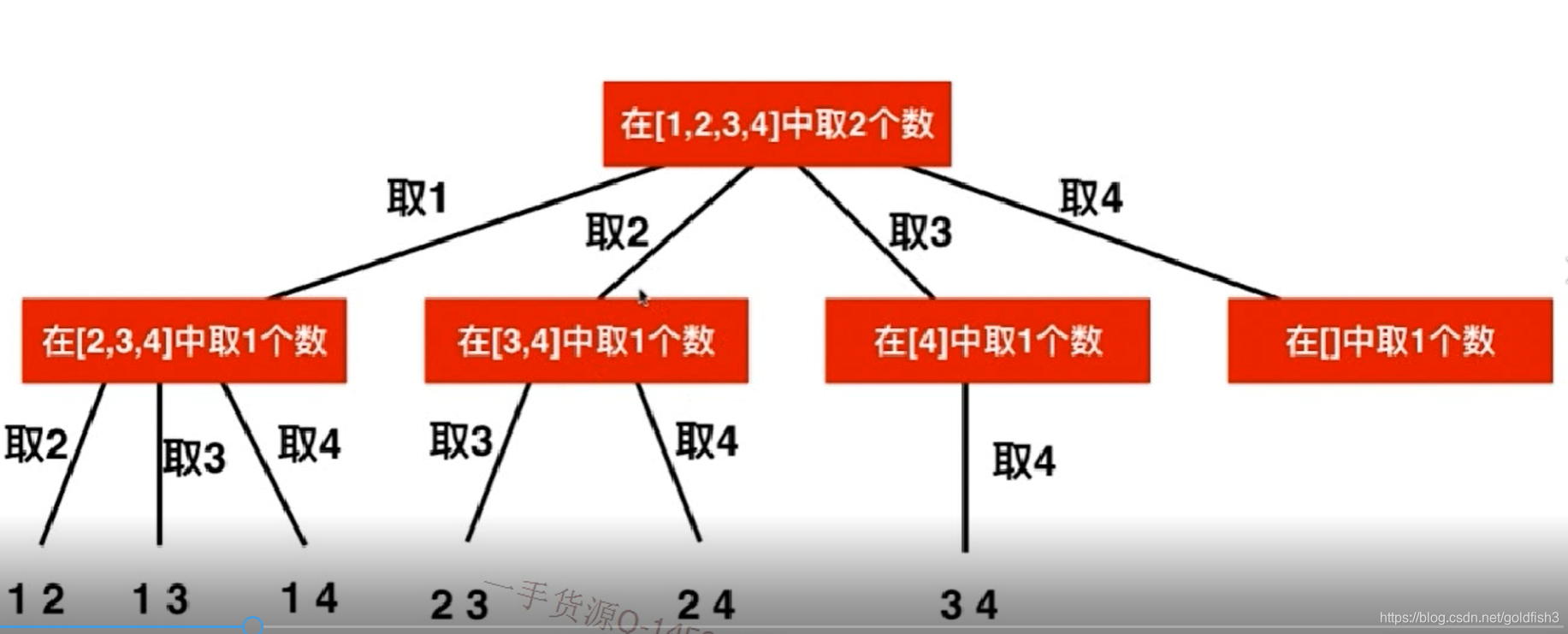
全组合问题

leetCode 77

class Solution {
    private List<List<Integer>> res = new ArrayList<List<Integer>>();
    
    public void combineCore(int n,int k,int start,ArrayList<Integer> cres){
        if(cres.size() == k){
            ArrayList<Integer> tmp = new ArrayList<Integer>();
            for(int i=0; i<cres.size(); i++){
                tmp.add(cres.get(i));
            }
            res.add(tmp);
            return;
        }
        for(int i=start; i<=n; i++){
            cres.add(i);
            combineCore(n,k,i+1,cres);
            cres.remove(cres.size()-1);
        }
        return;
    }
    
    public List<List<Integer>> combine(int n, int k) {
        if(n < 0 || k < 0 || k > n){
            return this.res;
        }
        this.combineCore(n,k,1,new ArrayList<Integer>());
        return this.res;
    }
}

剪枝
注意在 combineCore 的循环中，如果传入递归中的值是i，那么下一次就是从
[i,n] 中查找 k-cres.size() 个元素
如果 (n-i)<(k-cres.size()) 就意味着后续元素没有足够的数量，让结果的长度等于k
因此，可以将循环的终止条件改为 i<n-(k-cres.size())+1
``java
class Solution {
private List<List> res = new ArrayList<List>();

public void combineCore(int n,int k,int start,ArrayList<Integer> cres){
    if(cres.size() == k){
        ArrayList<Integer> tmp = new ArrayList<Integer>();
        for(int i=0; i<cres.size(); i++){
            tmp.add(cres.get(i));
        }
        res.add(tmp);
        return;
    }
    for(int i=start; i<=n-(k-cres.size())+1; i++){
        cres.add(i);
        combineCore(n,k,i+1,cres);
        cres.remove(cres.size()-1);
    }
    return;
}

public List<List<Integer>> combine(int n, int k) {
    if(n < 0 || k < 0 || k > n){
        return this.res;
    }
    this.combineCore(n,k,1,new ArrayList<Integer>());
    return this.res;
}

}

leetCode 39:组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1:

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
  [7],
  [2,2,3]
]
示例 2:

输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

答案

class Solution {
    private List<List<Integer>> res = new ArrayList<List<Integer>>();
    public void combinationCore(int[] candidates,ArrayList<Integer> cres, int start,int sum,int target){
        if (sum > target){
            return;
        }
        if (sum == target){
            ArrayList<Integer> tmp = new ArrayList<Integer>();
            for (Integer e : cres){
                tmp.add(e);
            }
            this.res.add(tmp);
            return;
        }
        for (int i=start; i<candidates.length; i++){
            cres.add(candidates[i]);
            combinationCore(candidates,cres,i,sum+candidates[i],target);
            cres.remove(cres.size()-1);
        }
    }

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        combinationCore(candidates,new ArrayList<Integer>(),0,0,target);
        return this.res;
    }
}

leetCode 78：子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

答案

class Solution {
    private List<List<Integer>> res = new ArrayList<List<Integer>>();

    private void subsetsCore(int[] nums,ArrayList<Integer> cres,int start){
        res.add(copyList(cres));
        if(cres.size() == nums.length){
            return;
        }
        for(int i=start; i<nums.length; i++){
            cres.add(nums[i]);
            subsetsCore(nums,cres,i+1);
            cres.remove(cres.size()-1);
        }
    }

    private List<Integer> copyList(List<Integer> list){
        ArrayList<Integer> copyList = new ArrayList<Integer>();
        for(Integer e : list){
            copyList.add(e);
        }
        return copyList;
    }

    public List<List<Integer>> subsets(int[] nums) {
        this.subsetsCore(nums,new ArrayList<Integer>(),0);
        return this.res;
    }

    
}