Bootstrap

二叉树的表示和实现

基本概念

　　在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

本文地址：http://www.cnblogs.com/archimedes/p/binary-tree.html，转载请注明源地址。

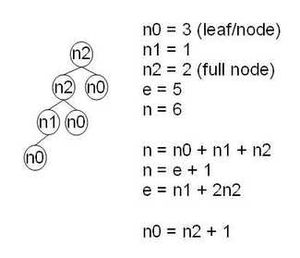
　　二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2i-1个结点；深度为k的二叉树至多有2k-1个结点；对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0 = n2 + 1。

树和二叉树的三个主要差别：

  • 树的结点个数至少为1，而二叉树的结点个数可以为0；

  • 树中结点的最大度数没有限制，而二叉树结点的最大度数为2；

  • 树的结点无左、右之分，而二叉树的结点有左、右之分。

<完全二叉树和满二叉树>

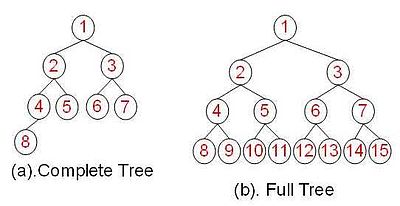
  • 满二叉树：一棵深度为k，且有2k-1个节点称之为满二叉树

  • 完全二叉树：深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应时，称之为完全二叉树

图论中的定义

　　二叉树在图论中是这样定义的：二叉树是一个连通的无环图，并且每一个顶点的度不大于3。有根二叉树还要满足根结点的度不大于2。有了根结点之后，每个顶点定义了唯一的父结点，和最多2个子结点。然而，没有足够的信息来区分左结点和右结点。如果不考虑连通性，允许图中有多个连通分量，这样的结构叫做森林。

二叉树(Binary Tree)的类型

　　二叉树是一个有根树，并且每个节点最多有2个子节点。非空的二元树，若树叶总数为 n0，分支度为2的总数为 n2，则 n0 = n2 + 1。

　　一棵深度为k，且有2k-1个节点的二叉树，称为满二叉树（Full Binary Tree）。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中，除最后一层外，若其馀层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树（Complete Binary Tree）。具有n个节点的完全二叉树的深度为log2n+1。深度为k的完全二叉树，至少有2k-1个节点，至多有2k-1个节点。

 完全二叉树满二叉树
总节点k 2h-1<= k < 2h-1k = 2h-1
树高hh = log2k+1h =  log2(k+1)

 

 

 

 

存储二叉树的方法

在编程语言中能用多种方法来构造二叉树。

顺序存储表示

　　二叉树可以用数组或线性表来存储，而且如果这是完全二叉树，这种方法不会浪费空间。用这种紧凑排列，如果一个结点的索引为i，它的子结点能在索引2i+1和2i+2找到，并且它的父节点（如果有）能在索引floor((i-1)/2)找到（假设根节点的索引为0）。这种方法更有利于紧凑存储和更好的访问的局部性，特别是在前序遍历中。然而，它需要连续的存储空间，这样在存储高度为h的n个结点组成的一般普通树时将会浪费很多空间。一种最极坏的情况下如果深度为h的二叉树每个节点只有右孩子需要占用2的h次幂减1，而实际却只有h个结点，空间的浪费太大，这是顺序存储结构的一大缺点。

存储结构

/* c6-1.h 二叉树的顺序存储表示 */
#define MAX_TREE_SIZE 100 /* 二叉树的最大结点数 */
typedef TElemType SqBiTree[MAX_TREE_SIZE]; /* 0号单元存储根结点 */
typedef struct {
    int level,order; /* 结点的层,本层序号(按满二叉树计算) */
}position;

基本操作

/* bo6-1.c 二叉树的顺序存储(存储结构由c6-1.h定义)的基本操作(23个) */
 Status InitBiTree(SqBiTree T)
 { /* 构造空二叉树T。因为T是固定数组，不会改变，故不需要& */
   int i;
   for(i=0;i<MAX_TREE_SIZE;i++)
     T[i]=Nil; /* 初值为空 */
   return OK;
 }

 void DestroyBiTree()
 { /* 由于SqBiTree是定长类型,无法销毁 */
 }

 Status CreateBiTree(SqBiTree T)
 { /* 按层序次序输入二叉树中结点的值(字符型或整型), 构造顺序存储的二叉树T */
   int i=0;
 #if CHAR
   int l;
   char s[MAX_TREE_SIZE];
   printf("请按层序输入结点的值(字符)，空格表示空结点，结点数≤%d:\n",MAX_TREE_SIZE);
   gets(s); /* 输入字符串 */
   l=strlen(s); /* 求字符串的长度 */
   for(;i<l;i++) /* 将字符串赋值给T */
   {
     T[i]=s[i];
     if(i!=0&&T[(i+1)/2-1]==Nil&&T[i]!=Nil) /* 此结点(不空)无双亲且不是根 */
     {
       printf("出现无双亲的非根结点%c\n",T[i]);
       exit(ERROR);
     }
   }
   for(i=l;i<MAX_TREE_SIZE;i++) /* 将空赋值给T的后面的结点 */
     T[i]=Nil;
 #else
   printf("请按层序输入结点的值(整型)，0表示空结点，输999结束。结点数≤%d:\n",MAX_TREE_SIZE);
   while(1)
   {
     scanf("%d",&T[i]);
     if(T[i]==999)
       break;
     if(i!=0&&T[(i+1)/2-1]==Nil&&T[i]!=Nil) /* 此结点(不空)无双亲且不是根 */
     {
       printf("出现无双亲的非根结点%d\n",T[i]);
       exit(ERROR);
     }
     i++;
   }
   while(i<MAX_TREE_SIZE)
   {
     T[i]=Nil; /* 将空赋值给T的后面的结点 */
     i++;
   }
 #endif
   return OK;
 }

 #define ClearBiTree InitBiTree /* 在顺序存储结构中，两函数完全一样 */

 Status BiTreeEmpty(SqBiTree T)
 { /* 初始条件: 二叉树T存在 */
   /* 操作结果: 若T为空二叉树,则返回TRUE,否则FALSE */
   if(T[0]==Nil) /* 根结点为空,则树空 */
     return TRUE;
   else
     return FALSE;
 }

 int BiTreeDepth(SqBiTree T)
 { /* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */
   int i,j=-1;
   for(i=MAX_TREE_SIZE-1;i>=0;i--) /* 找到最后一个结点 */
     if(T[i]!=Nil)
       break;
   i++; /* 为了便于计算 */
   do
     j++;
   while(i>=pow(2,j));
   return j;
 }

 Status Root(SqBiTree T,TElemType *e)
 { /* 初始条件: 二叉树T存在 */
   /* 操作结果:  当T不空,用e返回T的根,返回OK;否则返回ERROR,e无定义 */
   if(BiTreeEmpty(T)) /* T空 */
     return ERROR;
   else
   {
     *e=T[0];
     return OK;
   }
 }

 TElemType Value(SqBiTree T,position e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点(的位置) */
   /* 操作结果: 返回处于位置e(层,本层序号)的结点的值 */
   return T[(int)pow(2,e.level-1)+e.order-2];
 }

 Status Assign(SqBiTree T,position e,TElemType value)
 { /* 初始条件: 二叉树T存在,e是T中某个结点(的位置) */
   /* 操作结果: 给处于位置e(层,本层序号)的结点赋新值value */
   int i=(int)pow(2,e.level-1)+e.order-2; /* 将层、本层序号转为矩阵的序号 */
   if(value!=Nil&&T[(i+1)/2-1]==Nil) /* 给叶子赋非空值但双亲为空 */
     return ERROR;
   else if(value==Nil&&(T[i*2+1]!=Nil||T[i*2+2]!=Nil)) /*  给双亲赋空值但有叶子（不空） */
     return ERROR;
   T[i]=value;
   return OK;
 }

 TElemType Parent(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 若e是T的非根结点,则返回它的双亲,否则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=1;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e) /* 找到e */
       return T[(i+1)/2-1];
   return Nil; /* 没找到e */
 }

 TElemType LeftChild(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的左孩子。若e无左孩子,则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=0;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e) /* 找到e */
       return T[i*2+1];
   return Nil; /* 没找到e */
 }

 TElemType RightChild(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的右孩子。若e无右孩子,则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=0;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e) /* 找到e */
       return T[i*2+2];
   return Nil; /* 没找到e */
 }

 TElemType LeftSibling(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=1;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e&&i%2==0) /* 找到e且其序号为偶数(是右孩子) */
       return T[i-1];
   return Nil; /* 没找到e */
 }

 TElemType RightSibling(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=1;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e&&i%2) /* 找到e且其序号为奇数(是左孩子) */
       return T[i+1];
   return Nil; /* 没找到e */
 }

 void Move(SqBiTree q,int j,SqBiTree T,int i) /* InsertChild()用到。加 */
 { /* 把从q的j结点开始的子树移为从T的i结点开始的子树 */
   if(q[2*j+1]!=Nil) /* q的左子树不空 */
     Move(q,(2*j+1),T,(2*i+1)); /* 把q的j结点的左子树移为T的i结点的左子树 */
   if(q[2*j+2]!=Nil) /* q的右子树不空 */
     Move(q,(2*j+2),T,(2*i+2)); /* 把q的j结点的右子树移为T的i结点的右子树 */
   T[i]=q[j]; /* 把q的j结点移为T的i结点 */
   q[j]=Nil; /* 把q的j结点置空 */
 }

 Status InsertChild(SqBiTree T,TElemType p,Status LR,SqBiTree c)
 { /* 初始条件: 二叉树T存在,p是T中某个结点的值,LR为0或1,非空二叉树c与T */
   /*           不相交且右子树为空 */
   /* 操作结果: 根据LR为0或1,插入c为T中p结点的左或右子树。p结点的原有左或 */
   /*           右子树则成为c的右子树 */
   int j,k,i=0;
   for(j=0;j<(int)pow(2,BiTreeDepth(T))-1;j++) /* 查找p的序号 */
     if(T[j]==p) /* j为p的序号 */
       break;
   k=2*j+1+LR; /* k为p的左或右孩子的序号 */
   if(T[k]!=Nil) /* p原来的左或右孩子不空 */
     Move(T,k,T,2*k+2); /* 把从T的k结点开始的子树移为从k结点的右子树开始的子树 */
   Move(c,i,T,k); /* 把从c的i结点开始的子树移为从T的k结点开始的子树 */
   return OK;
 }

 typedef int QElemType; /* 设队列元素类型为整型(序号) */
 #include "c3-3.h" /* 顺序非循环队列 */
 #include "bo3-4.c" /* 顺序非循环队列的基本操作 */
 Status DeleteChild(SqBiTree T,position p,int LR)
 { /* 初始条件: 二叉树T存在,p指向T中某个结点,LR为1或0 */
   /* 操作结果: 根据LR为1或0,删除T中p所指结点的左或右子树 */
   int i;
   Status k=OK; /* 队列不空的标志 */
   SqQueue q;
   InitQueue(&q); /* 初始化队列，用于存放待删除的结点 */
   i=(int)pow(2,p.level-1)+p.order-2; /* 将层、本层序号转为矩阵的序号 */
   if(T[i]==Nil) /* 此结点空 */
     return ERROR;
   i=i*2+1+LR; /* 待删除子树的根结点在矩阵中的序号 */
   while(k)
   {
     if(T[2*i+1]!=Nil) /* 左结点不空 */
       EnQueue(&q,2*i+1); /* 入队左结点的序号 */
     if(T[2*i+2]!=Nil) /* 右结点不空 */
       EnQueue(&q,2*i+2); /* 入队右结点的序号 */
     T[i]=Nil; /* 删除此结点 */
     k=DeQueue(&q,&i); /* 队列不空 */
   }
   return OK;
 }

 Status(*VisitFunc)(TElemType); /* 函数变量 */
 void PreTraverse(SqBiTree T,int e)
 { /* PreOrderTraverse()调用 */
   VisitFunc(T[e]);
   if(T[2*e+1]!=Nil) /* 左子树不空 */
     PreTraverse(T,2*e+1);
   if(T[2*e+2]!=Nil) /* 右子树不空 */
     PreTraverse(T,2*e+2);
 }

 Status PreOrderTraverse(SqBiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 先序遍历T,对每个结点调用函数Visit一次且仅一次。 */
   /*           一旦Visit()失败,则操作失败 */
   VisitFunc=Visit;
   if(!BiTreeEmpty(T)) /* 树不空 */
     PreTraverse(T,0);
   printf("\n");
   return OK;
 }

 void InTraverse(SqBiTree T,int e)
 { /* InOrderTraverse()调用 */
   if(T[2*e+1]!=Nil) /* 左子树不空 */
     InTraverse(T,2*e+1);
   VisitFunc(T[e]);
   if(T[2*e+2]!=Nil) /* 右子树不空 */
     InTraverse(T,2*e+2);
 }

 Status InOrderTraverse(SqBiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 中序遍历T,对每个结点调用函数Visit一次且仅一次。 */
   /*           一旦Visit()失败,则操作失败 */
   VisitFunc=Visit;
   if(!BiTreeEmpty(T)) /* 树不空 */
     InTraverse(T,0);
   printf("\n");
   return OK;
 }

 void PostTraverse(SqBiTree T,int e)
 { /* PostOrderTraverse()调用 */
   if(T[2*e+1]!=Nil) /* 左子树不空 */
     PostTraverse(T,2*e+1);
   if(T[2*e+2]!=Nil) /* 右子树不空 */
     PostTraverse(T,2*e+2);
   VisitFunc(T[e]);
 }

 Status PostOrderTraverse(SqBiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 后序遍历T,对每个结点调用函数Visit一次且仅一次。 */
   /*           一旦Visit()失败,则操作失败 */
   VisitFunc=Visit;
   if(!BiTreeEmpty(T)) /* 树不空 */
     PostTraverse(T,0);
   printf("\n");
   return OK;
 }

 void LevelOrderTraverse(SqBiTree T,Status(*Visit)(TElemType))
 { /* 层序遍历二叉树 */
   int i=MAX_TREE_SIZE-1,j;
   while(T[i]==Nil)
     i--; /* 找到最后一个非空结点的序号 */
   for(j=0;j<=i;j++)  /* 从根结点起,按层序遍历二叉树 */
     if(T[j]!=Nil)
       Visit(T[j]); /* 只遍历非空的结点 */
   printf("\n");
 }

 void Print(SqBiTree T)
 { /* 逐层、按本层序号输出二叉树 */
   int j,k;
   position p;
   TElemType e;
   for(j=1;j<=BiTreeDepth(T);j++)
   {
     printf("第%d层: ",j);
     for(k=1;k<=pow(2,j-1);k++)
     {
       p.level=j;
       p.order=k;
       e=Value(T,p);
       if(e!=Nil)
         printf("%d:%d ",k,e);
     }
     printf("\n");
   }
 }
View Code

检验程序

/* main6-1.c 检验bo6-1.c的主程序，利用条件编译选择数据类型为char或int */
 /*#define CHAR 1 /* 字符型 */
 #define CHAR 0 /* 整型(二者选一) */
 #include"c1.h"
 #if CHAR
   typedef char TElemType;
   TElemType Nil=' '; /* 设字符型以空格符为空 */
 #else
   typedef int TElemType;
   TElemType Nil=0; /* 设整型以0为空 */
 #endif
 #include"c6-1.h"
 #include"bo6-1.c"

 Status visit(TElemType e)
 {
   printf("%d ",e);
   return OK;
 }

 void main()
 {
   Status i;
   int j;
   position p;
   TElemType e;
   SqBiTree T,s;
   InitBiTree(T);
   CreateBiTree(T);
   printf("建立二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   i=Root(T,&e);
   if(i)
     printf("二叉树的根为：%d\n",e);
   else
     printf("树空，无根\n");
   printf("层序遍历二叉树:\n");
   LevelOrderTraverse(T,visit);
   printf("中序遍历二叉树:\n");
   InOrderTraverse(T,visit);
   printf("后序遍历二叉树:\n");
   PostOrderTraverse(T,visit);
   printf("请输入待修改结点的层号 本层序号: ");
   scanf("%d%d",&p.level,&p.order);
   e=Value(T,p);
   printf("待修改结点的原值为%d请输入新值: ",e);
   scanf("%d",&e);
   Assign(T,p,e);
   printf("先序遍历二叉树:\n");
   PreOrderTraverse(T,visit);
   printf("结点%d的双亲为%d,左右孩子分别为",e,Parent(T,e));
   printf("%d,%d,左右兄弟分别为",LeftChild(T,e),RightChild(T,e));
   printf("%d,%d\n",LeftSibling(T,e),RightSibling(T,e));
   InitBiTree(s);
   printf("建立右子树为空的树s:\n");
   CreateBiTree(s);
   printf("树s插到树T中,请输入树T中树s的双亲结点 s为左(0)或右(1)子树: ");
   scanf("%d%d",&e,&j);
   InsertChild(T,e,j,s);
   Print(T);
   printf("删除子树,请输入待删除子树根结点的层号 本层序号 左(0)或右(1)子树: ");
   scanf("%d%d%d",&p.level,&p.order,&j);
   DeleteChild(T,p,j);
   Print(T);
   ClearBiTree(T);
   printf("清除二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   i=Root(T,&e);
   if(i)
     printf("二叉树的根为：%d\n",e);
   else
     printf("树空，无根\n");
 }
View Code

二叉链表存储表示

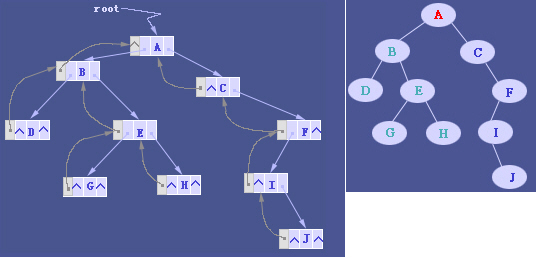
基于链表的二叉树逻辑结构示意

在使用记录或内存地址指针的编程语言中，二叉树通常用树结点结构来存储。有时也包含指向唯一的父节点的指针。如果一个结点的子结点个数小于2，一些子结点指针可能为空值，或者为特殊的哨兵结点。 使用链表能避免顺序储存浪费空间的问题，算法和结构相对简单，但使用二叉链表，由于缺乏父链的指引，在找回父节点时需要重新扫描树得知父节点的节点地址。

存储结构

typedef struct BiTNode {
    TElemType data;
    struct BiTNode *lchild,*rchild; /* 左右孩子指针 */
}BiTNode,*BiTree;

基本操作

/* bo6-2.c 二叉树的二叉链表存储(存储结构由c6-2.h定义)的基本操作(22个) */
 Status InitBiTree(BiTree *T)
 { /* 操作结果: 构造空二叉树T */
   *T=NULL;
   return OK;
 }

 void DestroyBiTree(BiTree *T)
 { /* 初始条件: 二叉树T存在。操作结果: 销毁二叉树T */
   if(*T) /* 非空树 */
   {
     if((*T)->lchild) /* 有左孩子 */
       DestroyBiTree(&(*T)->lchild); /* 销毁左孩子子树 */
     if((*T)->rchild) /* 有右孩子 */
       DestroyBiTree(&(*T)->rchild); /* 销毁右孩子子树 */
     free(*T); /* 释放根结点 */
     *T=NULL; /* 空指针赋0 */
   }
 }

 void CreateBiTree(BiTree *T)
 { /* 算法6.4:按先序次序输入二叉树中结点的值（可为字符型或整型，在主程中 */
   /* 定义），构造二叉链表表示的二叉树T。变量Nil表示空（子）树。有改动 */
   TElemType ch;
 #ifdef CHAR
   scanf("%c",&ch);
 #endif
 #ifdef INT
   scanf("%d",&ch);
 #endif
   if(ch==Nil) /* 空 */
     *T=NULL;
   else
   {
     *T=(BiTree)malloc(sizeof(BiTNode));
     if(!*T)
       exit(OVERFLOW);
     (*T)->data=ch; /* 生成根结点 */
     CreateBiTree(&(*T)->lchild); /* 构造左子树 */
     CreateBiTree(&(*T)->rchild); /* 构造右子树 */
   }
 }

 Status BiTreeEmpty(BiTree T)
 { /* 初始条件: 二叉树T存在 */
   /* 操作结果: 若T为空二叉树,则返回TRUE,否则FALSE */
   if(T)
     return FALSE;
   else
     return TRUE;
 }

 #define ClearBiTree DestroyBiTree

 int BiTreeDepth(BiTree T)
 { /* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */
   int i,j;
   if(!T)
     return 0;
   if(T->lchild)
     i=BiTreeDepth(T->lchild);
   else
     i=0;
   if(T->rchild)
     j=BiTreeDepth(T->rchild);
   else
     j=0;
   return i>j?i+1:j+1;
 }

 TElemType Root(BiTree T)
 { /* 初始条件: 二叉树T存在。操作结果: 返回T的根 */
   if(BiTreeEmpty(T))
     return Nil;
   else
     return T->data;
 }

 TElemType Value(BiTree p)
 { /* 初始条件: 二叉树T存在，p指向T中某个结点 */
   /* 操作结果: 返回p所指结点的值 */
   return p->data;
 }

 void Assign(BiTree p,TElemType value)
 { /* 给p所指结点赋值为value */
   p->data=value;
 }

 typedef BiTree QElemType; /* 设队列元素为二叉树的指针类型 */
 #include"c3-2.h"
 #include"bo3-2.c"
 TElemType Parent(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 若e是T的非根结点,则返回它的双亲,否则返回＂空＂ */
   LinkQueue q;
   QElemType a;
   if(T) /* 非空树 */
   {
     InitQueue(&q); /* 初始化队列 */
     EnQueue(&q,T); /* 树根入队 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&a); /* 出队,队列元素赋给a */
       if(a->lchild&&a->lchild->data==e||a->rchild&&a->rchild->data==e)
       /* 找到e(是其左或右孩子) */
         return a->data; /* 返回e的双亲的值 */
       else /* 没找到e,则入队其左右孩子指针(如果非空) */
       {
         if(a->lchild)
           EnQueue(&q,a->lchild);
         if(a->rchild)
           EnQueue(&q,a->rchild);
       }
     }
   }
   return Nil; /* 树空或没找到e */
 }

 BiTree Point(BiTree T,TElemType s)
 { /* 返回二叉树T中指向元素值为s的结点的指针。另加 */
   LinkQueue q;
   QElemType a;
   if(T) /* 非空树 */
   {
     InitQueue(&q); /* 初始化队列 */
     EnQueue(&q,T); /* 根结点入队 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&a); /* 出队,队列元素赋给a */
       if(a->data==s)
         return a;
       if(a->lchild) /* 有左孩子 */
         EnQueue(&q,a->lchild); /* 入队左孩子 */
       if(a->rchild) /* 有右孩子 */
         EnQueue(&q,a->rchild); /* 入队右孩子 */
     }
   }
   return NULL;
 }

 TElemType LeftChild(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的左孩子。若e无左孩子,则返回＂空＂ */
   BiTree a;
   if(T) /* 非空树 */
   {
     a=Point(T,e); /* a是结点e的指针 */
     if(a&&a->lchild) /* T中存在结点e且e存在左孩子 */
       return a->lchild->data; /* 返回e的左孩子的值 */
   }
   return Nil; /* 其余情况返回空 */
 }

 TElemType RightChild(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的右孩子。若e无右孩子,则返回＂空＂ */
   BiTree a;
   if(T) /* 非空树 */
   {
     a=Point(T,e); /* a是结点e的指针 */
     if(a&&a->rchild) /* T中存在结点e且e存在右孩子 */
       return a->rchild->data; /* 返回e的右孩子的值 */
   }
   return Nil; /* 其余情况返回空 */
 }

 TElemType LeftSibling(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回＂空＂ */
   TElemType a;
   BiTree p;
   if(T) /* 非空树 */
   {
     a=Parent(T,e); /* a为e的双亲 */
     p=Point(T,a); /* p为指向结点a的指针 */
     if(p->lchild&&p->rchild&&p->rchild->data==e) /* p存在左右孩子且右孩子是e */
       return p->lchild->data; /* 返回p的左孩子(e的左兄弟) */
   }
   return Nil; /* 树空或没找到e的左兄弟 */
 }

 TElemType RightSibling(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回＂空＂ */
   TElemType a;
   BiTree p;
   if(T) /* 非空树 */
   {
     a=Parent(T,e); /* a为e的双亲 */
     p=Point(T,a); /* p为指向结点a的指针 */
     if(p->lchild&&p->rchild&&p->lchild->data==e) /* p存在左右孩子且左孩子是e */
       return p->rchild->data; /* 返回p的右孩子(e的右兄弟) */
   }
   return Nil; /* 树空或没找到e的右兄弟 */
 }

 Status InsertChild(BiTree p,int LR,BiTree c) /* 形参T无用 */
 { /* 初始条件: 二叉树T存在,p指向T中某个结点,LR为0或1,非空二叉树c与T */
   /*           不相交且右子树为空 */
   /* 操作结果: 根据LR为0或1,插入c为T中p所指结点的左或右子树。p所指结点的 */
   /*           原有左或右子树则成为c的右子树 */
   if(p) /* p不空 */
   {
     if(LR==0)
     {
       c->rchild=p->lchild;
       p->lchild=c;
     }
     else /* LR==1 */
     {
       c->rchild=p->rchild;
       p->rchild=c;
     }
     return OK;
   }
   return ERROR; /* p空 */
 }

 Status DeleteChild(BiTree p,int LR) /* 形参T无用 */
 { /* 初始条件: 二叉树T存在,p指向T中某个结点,LR为0或1 */
   /* 操作结果: 根据LR为0或1,删除T中p所指结点的左或右子树 */
   if(p) /* p不空 */
   {
     if(LR==0) /* 删除左子树 */
       ClearBiTree(&p->lchild);
     else /* 删除右子树 */
       ClearBiTree(&p->rchild);
     return OK;
   }
   return ERROR; /* p空 */
 }

 void PreOrderTraverse(BiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树T存在,Visit是对结点操作的应用函数。算法6.1，有改动 */
   /* 操作结果: 先序递归遍历T,对每个结点调用函数Visit一次且仅一次 */
   if(T) /* T不空 */
   {
     Visit(T->data); /* 先访问根结点 */
     PreOrderTraverse(T->lchild,Visit); /* 再先序遍历左子树 */
     PreOrderTraverse(T->rchild,Visit); /* 最后先序遍历右子树 */
   }
 }

 void InOrderTraverse(BiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 中序递归遍历T,对每个结点调用函数Visit一次且仅一次 */
   if(T)
   {
     InOrderTraverse(T->lchild,Visit); /* 先中序遍历左子树 */
     Visit(T->data); /* 再访问根结点 */
     InOrderTraverse(T->rchild,Visit); /* 最后中序遍历右子树 */
   }
 }

 typedef BiTree SElemType; /* 设栈元素为二叉树的指针类型 */
 #include"c3-1.h"
 #include"bo3-1.c"
 Status InOrderTraverse1(BiTree T,Status(*Visit)(TElemType))
 { /* 采用二叉链表存储结构，Visit是对数据元素操作的应用函数。算法6.3 */
   /* 中序遍历二叉树T的非递归算法(利用栈)，对每个数据元素调用函数Visit */
   SqStack S;
   InitStack(&S);
   while(T||!StackEmpty(S))
   {
     if(T)
     { /* 根指针进栈,遍历左子树 */
       Push(&S,T);
       T=T->lchild;
     }
     else
     { /* 根指针退栈,访问根结点,遍历右子树 */
       Pop(&S,&T);
       if(!Visit(T->data))
         return ERROR;
       T=T->rchild;
     }
   }
   printf("\n");
   return OK;
 }

 Status InOrderTraverse2(BiTree T,Status(*Visit)(TElemType))
 { /* 采用二叉链表存储结构，Visit是对数据元素操作的应用函数。算法6.2 */
   /* 中序遍历二叉树T的非递归算法(利用栈)，对每个数据元素调用函数Visit */
   SqStack S;
   BiTree p;
   InitStack(&S);
   Push(&S,T); /* 根指针进栈 */
   while(!StackEmpty(S))
   {
     while(GetTop(S,&p)&&p)
       Push(&S,p->lchild); /* 向左走到尽头 */
     Pop(&S,&p); /* 空指针退栈 */
     if(!StackEmpty(S))
     { /* 访问结点,向右一步 */
       Pop(&S,&p);
       if(!Visit(p->data))
         return ERROR;
       Push(&S,p->rchild);
     }
   }
   printf("\n");
   return OK;
 }

 void PostOrderTraverse(BiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 后序递归遍历T,对每个结点调用函数Visit一次且仅一次 */
   if(T) /* T不空 */
   {
     PostOrderTraverse(T->lchild,Visit); /* 先后序遍历左子树 */
     PostOrderTraverse(T->rchild,Visit); /* 再后序遍历右子树 */
     Visit(T->data); /* 最后访问根结点 */
   }
 }

 void LevelOrderTraverse(BiTree T,Status(*Visit)(TElemType))
 { /* 初始条件：二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果：层序递归遍历T(利用队列),对每个结点调用函数Visit一次且仅一次 */
   LinkQueue q;
   QElemType a;
   if(T)
   {
     InitQueue(&q);
     EnQueue(&q,T);
     while(!QueueEmpty(q))
     {
       DeQueue(&q,&a);
       Visit(a->data);
       if(a->lchild!=NULL)
         EnQueue(&q,a->lchild);
       if(a->rchild!=NULL)
         EnQueue(&q,a->rchild);
     }
     printf("\n");
   }
 }
View Code

检验程序

/* main6-2.c 检验bo6-2.c的主程序,利用条件编译选择数据类型(另一种方法) */
 #define CHAR /* 字符型 */
 /* #define INT /* 整型（二者选一） */
 #include"c1.h"
 #ifdef CHAR
   typedef char TElemType;
   TElemType Nil=' '; /* 字符型以空格符为空 */
 #endif
 #ifdef INT
   typedef int TElemType;
   TElemType Nil=0; /* 整型以0为空 */
 #endif
 #include"c6-2.h"
 #include"bo6-2.c"

 Status visitT(TElemType e)
 {
 #ifdef CHAR
   printf("%c ",e);
 #endif
 #ifdef INT
   printf("%d ",e);
 #endif
   return OK;
 }

 void main()
 {
   int i;
   BiTree T,p,c;
   TElemType e1,e2;
   InitBiTree(&T);
   printf("构造空二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   e1=Root(T);
   if(e1!=Nil)
 #ifdef CHAR
     printf("二叉树的根为: %c\n",e1);
 #endif
 #ifdef INT
     printf("二叉树的根为: %d\n",e1);
 #endif
   else
     printf("树空，无根\n");
 #ifdef CHAR
   printf("请先序输入二叉树(如:ab三个空格表示a为根结点,b为左子树的二叉树)\n");
 #endif
 #ifdef INT
   printf("请先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)\n");
 #endif
   CreateBiTree(&T);
   printf("建立二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   e1=Root(T);
   if(e1!=Nil)
 #ifdef CHAR
     printf("二叉树的根为: %c\n",e1);
 #endif
 #ifdef INT
     printf("二叉树的根为: %d\n",e1);
 #endif
   else
     printf("树空，无根\n");
   printf("中序递归遍历二叉树:\n");
   InOrderTraverse(T,visitT);
   printf("\n中序非递归遍历二叉树:\n");
   InOrderTraverse1(T,visitT);
   printf("中序非递归遍历二叉树(另一种方法):\n");
   InOrderTraverse2(T,visitT);
   printf("后序递归遍历二叉树:\n");
   PostOrderTraverse(T,visitT);
   printf("\n层序遍历二叉树:\n");
   LevelOrderTraverse(T,visitT);
   printf("请输入一个结点的值: ");
 #ifdef CHAR
   scanf("%*c%c",&e1);
 #endif
 #ifdef INT
   scanf("%d",&e1);
 #endif
   p=Point(T,e1); /* p为e1的指针 */
 #ifdef CHAR
   printf("结点的值为%c\n",Value(p));
 #endif
 #ifdef INT
   printf("结点的值为%d\n",Value(p));
 #endif
   printf("欲改变此结点的值，请输入新值: ");
 #ifdef CHAR
   scanf("%*c%c%*c",&e2);
 #endif
 #ifdef INT
   scanf("%d",&e2);
 #endif
   Assign(p,e2);
   printf("层序遍历二叉树:\n");
   LevelOrderTraverse(T,visitT);
   e1=Parent(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的双亲是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的双亲是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有双亲\n",e2);
 #endif
 #ifdef INT
     printf("%d没有双亲\n",e2);
 #endif
   e1=LeftChild(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的左孩子是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的左孩子是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有左孩子\n",e2);
 #endif
 #ifdef INT
     printf("%d没有左孩子\n",e2);
 #endif
   e1=RightChild(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的右孩子是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的右孩子是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有右孩子\n",e2);
 #endif
 #ifdef INT
     printf("%d没有右孩子\n",e2);
 #endif
   e1=LeftSibling(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的左兄弟是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的左兄弟是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有左兄弟\n",e2);
 #endif
 #ifdef INT
     printf("%d没有左兄弟\n",e2);
 #endif
   e1=RightSibling(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的右兄弟是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的右兄弟是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有右兄弟\n",e2);
 #endif
 #ifdef INT
     printf("%d没有右兄弟\n",e2);
 #endif
   InitBiTree(&c);
   printf("构造一个右子树为空的二叉树c:\n");
 #ifdef CHAR
   printf("请先序输入二叉树(如:ab三个空格表示a为根结点,b为左子树的二叉树)\n");
 #endif
 #ifdef INT
   printf("请先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)\n");
 #endif
   CreateBiTree(&c);
   printf("先序递归遍历二叉树c:\n");
   PreOrderTraverse(c,visitT);
   printf("\n树c插到树T中,请输入树T中树c的双亲结点 c为左(0)或右(1)子树: ");
 #ifdef CHAR
   scanf("%*c%c%d",&e1,&i);
 #endif
 #ifdef INT
   scanf("%d%d",&e1,&i);
 #endif
   p=Point(T,e1); /* p是T中树c的双亲结点指针 */
   InsertChild(p,i,c);
   printf("先序递归遍历二叉树:\n");
   PreOrderTraverse(T,visitT);
   printf("\n删除子树,请输入待删除子树的双亲结点  左(0)或右(1)子树: ");
 #ifdef CHAR
   scanf("%*c%c%d",&e1,&i);
 #endif
 #ifdef INT
   scanf("%d%d",&e1,&i);
 #endif
   p=Point(T,e1);
   DeleteChild(p,i);
   printf("先序递归遍历二叉树:\n");
   PreOrderTraverse(T,visitT);
   printf("\n");
   DestroyBiTree(&T);
 }
View Code

编程实践

TOJ1222: 数据结构练习题——先序遍历二叉树

    
#include <stdio.h>
#include <string.h>
#include <ctype.h>
#include <math.h>

int BiTree[10000];

void PreTraverse(int T[], int e)  //递归先序遍历二叉树T中序号为e的子树 
{
    printf(" %d",T[e]);    //访问树T中序号为e的节点 
  if(T[2*e+1]!=0) PreTraverse(T,2*e+1);  //序号为e的节点的左子树不空 
  if(T[2*e+2]!=0) PreTraverse(T,2*e+2);  //序号为e的节点的右子树不空 
}

void PreOrderTraverse(int T[])
{
    PreTraverse(T,0);   //递归先序遍历树T中序号为0的树 
    printf("\n");
}

int TreeDeep(int T[], int n)
{
    int i;
    for(i=n-1; i>=0; i--)
    {
        if(T[i]!=0)  break;
    }
    return (int)(log(i+1)/log(2)+1.1);
}

int main()
{
    int n,t,i;
    scanf("%d",&n);
    while(n--)
    {
        i=0;
        while(scanf("%d",&t) && t!=-1)
        {
              BiTree[i++]=t;
        }
        printf("%d",TreeDeep(BiTree,i));
        PreOrderTraverse(BiTree);
    }
    return 0;
}
View Code

TOJ1223: 数据结构练习题——中序遍历二叉树

#include <stdio.h>
#include <string.h>
#include <ctype.h>
#include <math.h>

int BiTree[10000];

void InTraverse(int T[], int e)
{
  if(T[2*e+1]!=0) InTraverse(T,2*e+1);
  printf(" %d",T[e]);
  if(T[2*e+2]!=0) InTraverse(T,2*e+2);
}

void InOrderTraverse(int T[])
{
    InTraverse(T,0);
    printf("\n");
}

int TreeDeep(int T[], int n)
{
    int i;
    for(i=n-1; i>=0; i--)
    {
        if(T[i]!=0)  break;
    }
    return (int)(log(i+1)/log(2)+1.1);
}

int main()
{
    int n,t,i;
    scanf("%d",&n);
    while(n--)
    {
        i=0;
        while(scanf("%d",&t) && t!=-1)
        {
              BiTree[i++]=t;
        }
        printf("%d",TreeDeep(BiTree,i));
        InOrderTraverse(BiTree);
    }
    return 0;
}
View Code

TOJ1224: 数据结构练习题——后序遍历二叉树

#include <stdio.h>
#include <string.h>
#include <ctype.h>
#include <math.h>

int BiTree[10000];

void PostTraverse(int T[], int e) 
{
  if(T[2*e+1]!=0) PostTraverse(T,2*e+1);  
  if(T[2*e+2]!=0) PostTraverse(T,2*e+2); 
  printf(" %d",T[e]);  
}

void PostOrderTraverse(int T[])
{
    PostTraverse(T,0); 
    printf("\n");
}

int TreeDeep(int T[], int n)
{
    int i;
    for(i=n-1; i>=0; i--)
    {
        if(T[i]!=0)  break;
    }
    return (int)(log(i+1)/log(2)+1.1);
}

int main()
{
    int n,t,i;
    scanf("%d",&n);
    while(n--)
    {
        i=0;
        while(scanf("%d",&t) && t!=-1)
        {
              BiTree[i++]=t;
        }
        printf("%d",TreeDeep(BiTree,i));
        PostOrderTraverse(BiTree);
    }
    return 0;
}
View Code

 

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
2024年最强网络安全学习路线，详细到直接上清华的教材！
2024 高教社杯 数学建模国赛 （B题）深度剖析|生产过程中的决策问题|数学建模完整代码+建模过程全解全析
springboot web跨域访问问题解决--addCorsMappings和CorsFilter
JAVA并发编程实战-应用线程池
Request processing failed nested exception is org.mybatis.spring
随机抽题记录
计算机网络自顶向下方法(第六版) 课后题答案 | 第五章
sql数据库-用户管理-DCL
支付宝接口接入方法 步骤十分详细
使用druid连接池的超时回收机制排查连接泄露问题
;