数据结构-C语言-排序（4）

代码位置：

test-c-2024: 对C语言习题代码的练习 (gitee.com)

一、前言：

1.1-排序定义：

排序就是将一组杂乱无章的数据按照一定的规律（升序或降序）组织起来。(注：我们这里的排序采用的都为升序)

1.2-排序分类：

常见的排序算法：

插入排序
a. 直接插入排序
b. 希尔排序
选择排序
a. 选择排序
b. 堆排序
交换排序
a. 冒泡排序
b. 快速排序
归并排序
a. 归并排序
非比较排序
a.计数排序
b.基数排序

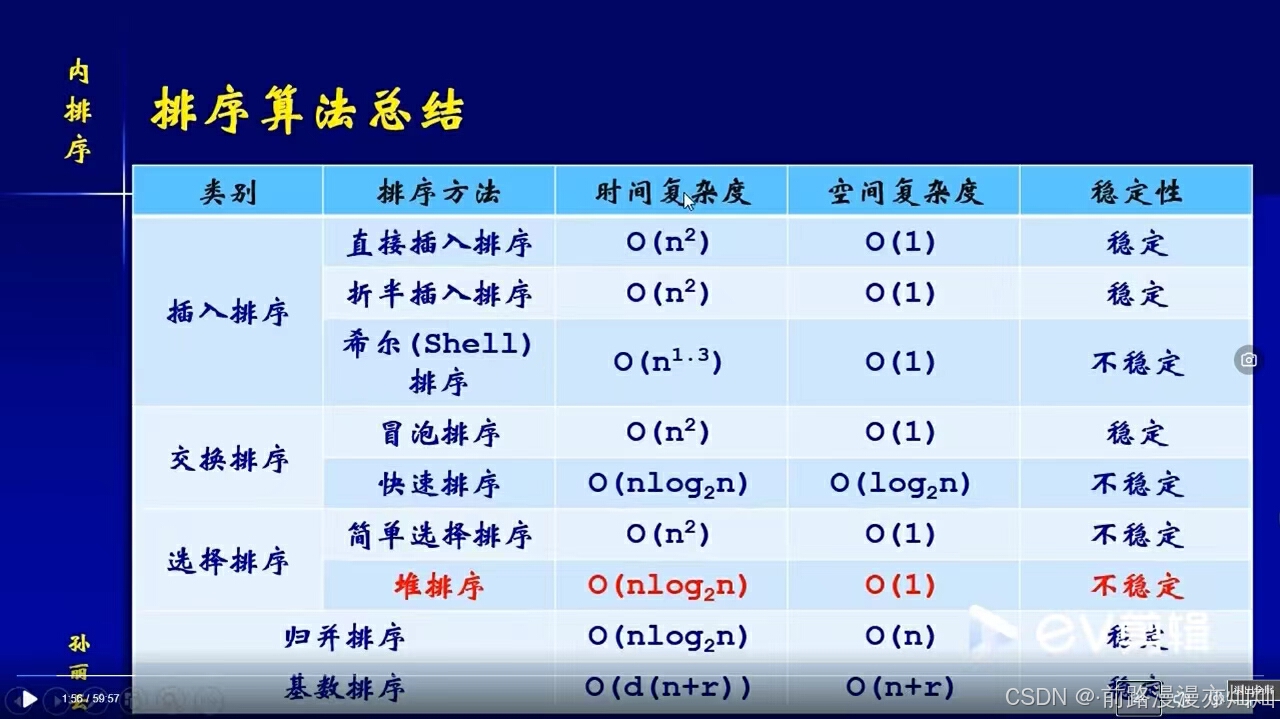
1.3-算法比较：

1.4-目的：

今天，我们这里要实现的是归并排序、计数排序。

二、归并排序-递归：

2.1-定义：

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

2.2-思路：

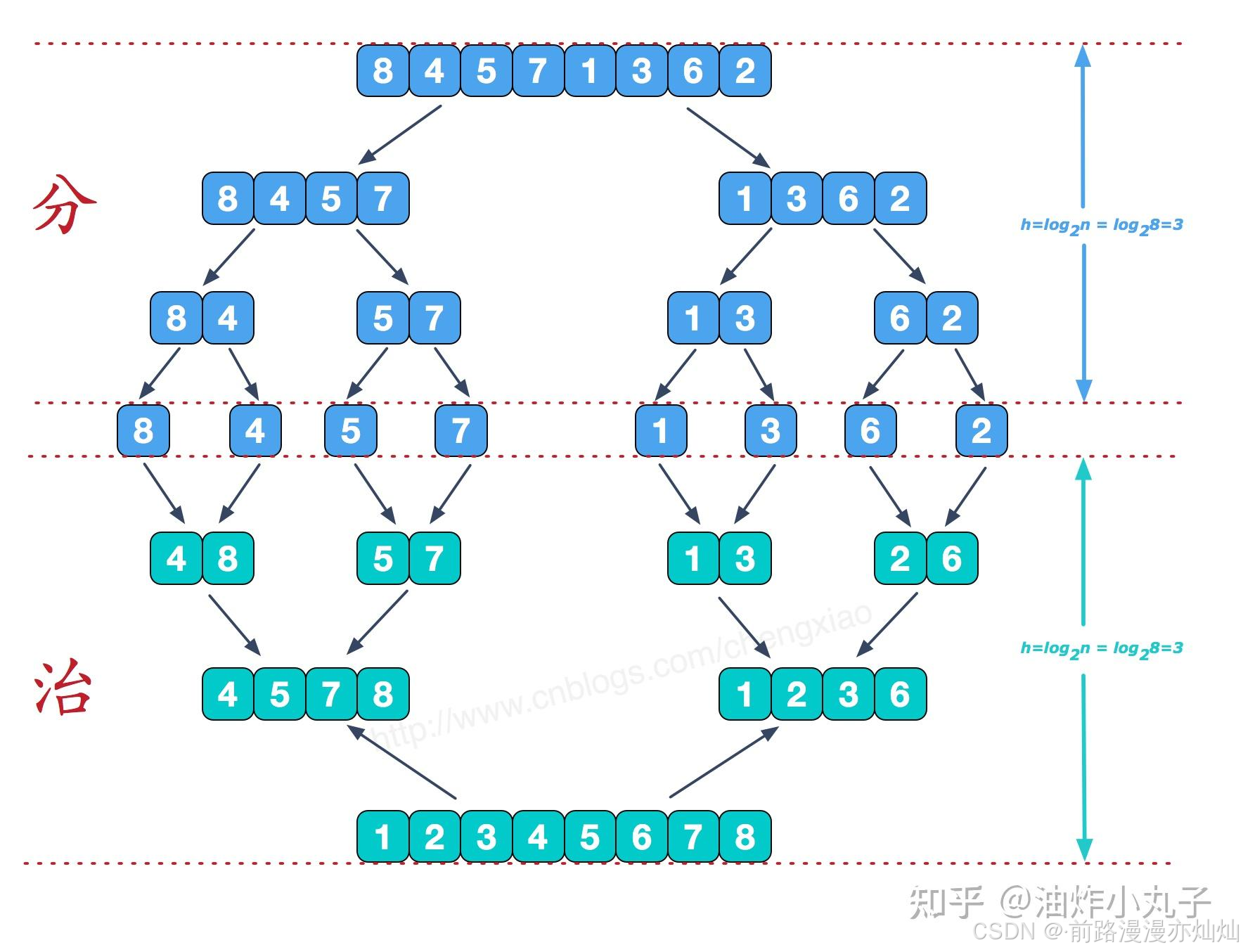
归并排序两个基本过程：

1、分：将原数组分割成两个平分子数组的过程。

2、治：将分割后的数组两两结合成一个有序的数组的过程。

归并排序两个基本操作：

将待排序的线性表不断地切分成若干个子表，直到每个子表只包含一个元素，这时，可以认为只包含一个元素的子表是有序表。
将子表两两合并，每合并一次，就会产生一个新的且更长的有序表，重复这一步骤，直到最后只剩下一个子表，这个子表就是排好序的线性表。

2.3-过程图：

2.4-代码实现：

void _MagerSort(int* a, int begin,int end,int*tem)
{
	if (begin >= end)
		return;

	int mid = (begin + end) / 2;
	//子区间递归
	_MagerSort(a, begin, mid, tem);
	_MagerSort(a, mid+1, end, tem);

	//归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while(begin1<=end1&&begin2<=end2)
	{
		if (a[begin1] >= a[begin2])
		{
			tem[i++] = a[begin2++];
		}
		else
		{
			tem[i++] = a[begin1++];
		}
	}

	while (begin1 <= end1)
	{
		tem[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tem[i++] = a[begin2++];
	}
	memcpy(a + begin, tem + begin, sizeof(int) * (end - begin + 1));
}

//递归实现
void MagerSort(int* a, int n)				//归并排序---时间复杂度(O(N*logN))
{
	int* tem = (int*)malloc(sizeof(int) * n);
	if (tem == NULL)
	{
		perror("malloc MagerSort");
		return;
	}
	_MagerSort(a, 0, n - 1, tem);


	free(tem);
}

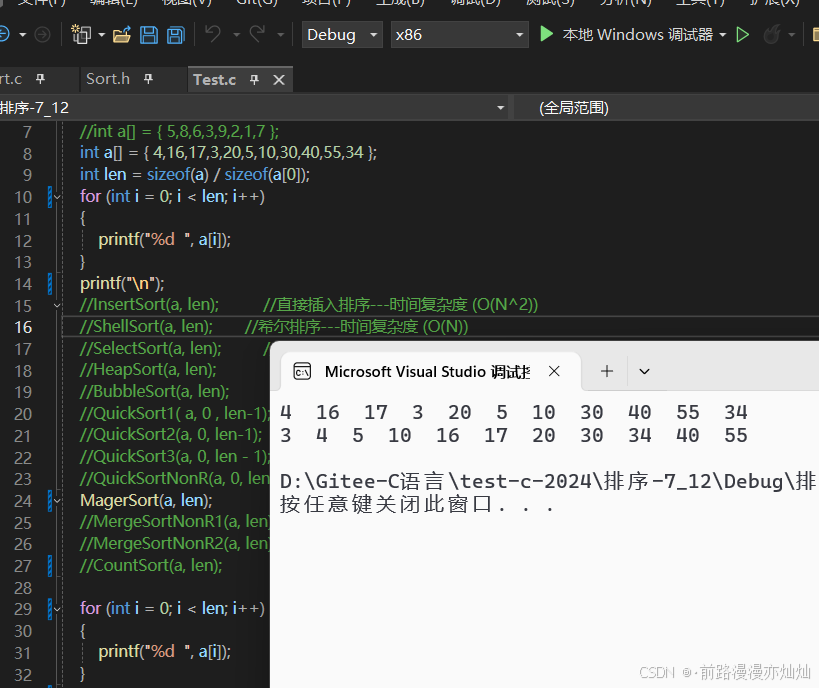
2.5-效果图：

三、归并排序-非递归：

3.1-定义：

3.2-思路：

我们知道，递归实现的缺点就是会一直调用栈，而栈内存往往是很小的，如果调用次数过多就会出现栈溢出的现象。所以，我们尝试着用循环的办法去实现归并排序。

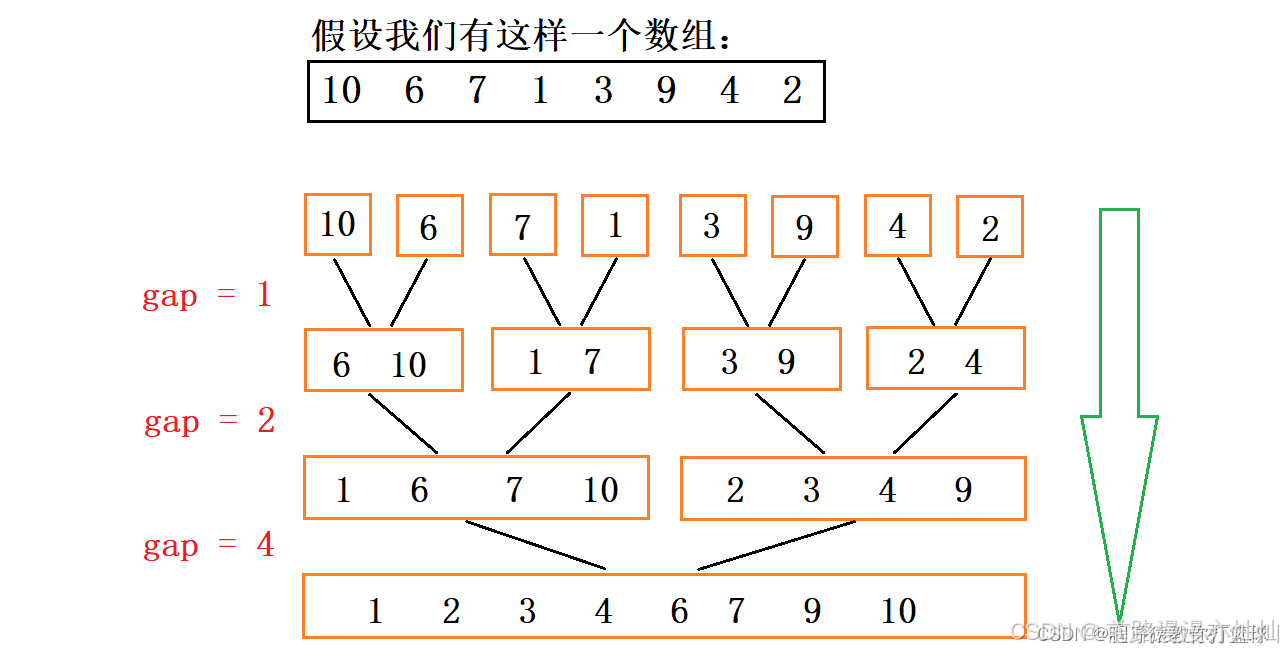
我们可以通过间距值gap=1来实现将数组分割若干个只含一个数的子数组的操作，然后通过改变gap的值来实现两两合并的操作。

注意：在循环过程中我们需要考虑是否有越界的问题，如果有的话我们可以通过改变begin和end的值的方式来调整范围，修正路线。

拷贝时我们有两种拷贝方式：一种是全部拷贝（梭哈），另一种是部分拷贝。

3.3-过程图：

3.4-代码实现：


//非递归实现
//全部拷贝（梭哈）
void MergeSortNonR1(int* a, int n)		//归并排序---时间复杂度(O(N*logN))
{
	int* tem = (int*)malloc(sizeof(int) * n);
	if (tem == NULL)
	{
		perror("malloc fail\n");
		return;
	}

	
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i+=2*gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//修正路线
			if (end1 >= n)
			{
				end1 = n-1;
				begin2 = n;
				end2 = n-1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n-1;
			}
			else if (end2 >= n)
			{
				end2 = n-1;
			}
			//归并
			int j = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] >= a[begin2])
				{
					tem[j++] = a[begin2++];
				}
				else
				{
					tem[j++] = a[begin1++];
				}
			}
			while (begin1 <= end1)
			{
				tem[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tem[j++] = a[begin2++];
			}	
			
		}
		memcpy(a, tem, sizeof(int) * n);
		gap *= 2;
	}

	free(tem);
}

//部份拷贝
void MergeSortNonR2(int* a, int n)		//归并排序---时间复杂度(O(N*logN))
{
	int* tem = (int*)malloc(sizeof(int) * n);
	if (tem == NULL)
	{
		perror("malloc fail\n");
		return;
	}


	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//修正路线
			if (end1 >= n)
			{
				break;
			}
			else if (begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}
			//归并
			int j = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] >= a[begin2])
				{
					tem[j++] = a[begin2++];
				}
				else
				{
					tem[j++] = a[begin1++];
				}
			}
			while (begin1 <= end1)
			{
				tem[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tem[j++] = a[begin2++];
			}
			memcpy(a+i, tem+i, sizeof(int) * (end2 - i + 1));
		}
		
		gap *= 2;
	}

	free(tem);
}

3.5-效果图：

四、计数排序：

4.1-定义：

计数排序是一种非比较排序算法。它通过计算每个唯一元素的出现次数对数组进行排序。它对唯一元素的计数进行部分哈希处理，然后执行计算以找到最终排序数组中每个元素的索引。它是一个相当快的算法，但不适合大型数据集。它作为基数排序中的一个子程序使用。

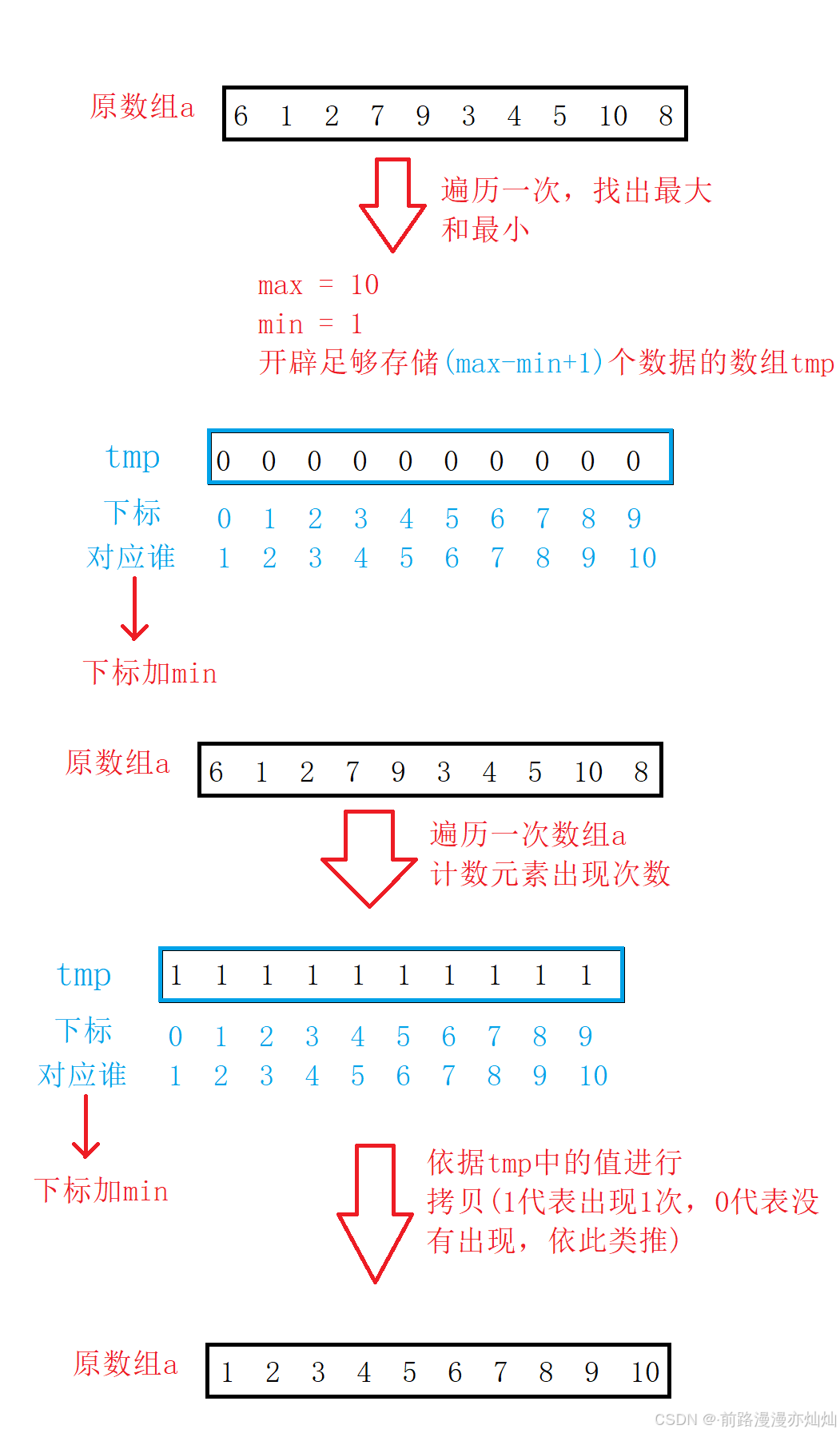
4.2-思路：

1.开辟计数数组：如果数据为：（100，102，106，110，107）的话这里从0开始开辟的话就会开辟一个长度111个的数组其中有100个是浪费的，这样的话如果数据过大的话这个排序的效率就会非常的低。所以，这里我们数组长度的开辟采用最大值-最小值的方式，这样就避免了上述情况。

2.出计数数组：出数组时我们是从计数数组的第一个下标中统计的个数依次往后出，出数组时我们需要下标加上最小值min，这样就实现排序啦！

4.3-过程图：

4.4-代码实现：


// 时间复杂度：O(N+range)
// 空间复杂度：O(range)
void CountSort(int* a, int n)					// 计数排序
{
	int max = a[0];
	int min = a[0];
	for (int i = 1; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min+1;
	int* tem = (int*)malloc(sizeof(int) * range);
	if (tem == NULL)
	{
		perror("malloc");
		return;
	}
	//开辟的数组初始化为0
	for (int i = 0; i < range; i++)
	{
		tem[i] = 0;
	}
	for (int i = 0; i < n; i++)
	{

		int j = a[i] - min;
		tem[j]++;
	}
	int m = 0;
	for (int i = 0; i < range; i++)
	{
		while(tem[i]>0)
		{
			if (tem[i] != 0)
			{
				a[m++] = i + min;
				tem[i]--;
			}
		}
	}
}

4.5-效果图：

五、结语：

上述内容，即是我个人对数据结构排序中归并排序、计数排序的个人见解以及自我实现。若有大佬发现哪里有问题可以私信或评论指教一下我这个小萌新。非常感谢各位uu们的点赞，关注，收藏，我会更加努力的学习编程语言，还望各位多多关照，让我们一起进步吧！