什么是蚁群算法?
蚁群系统(Ant System(AS)或Ant Colony
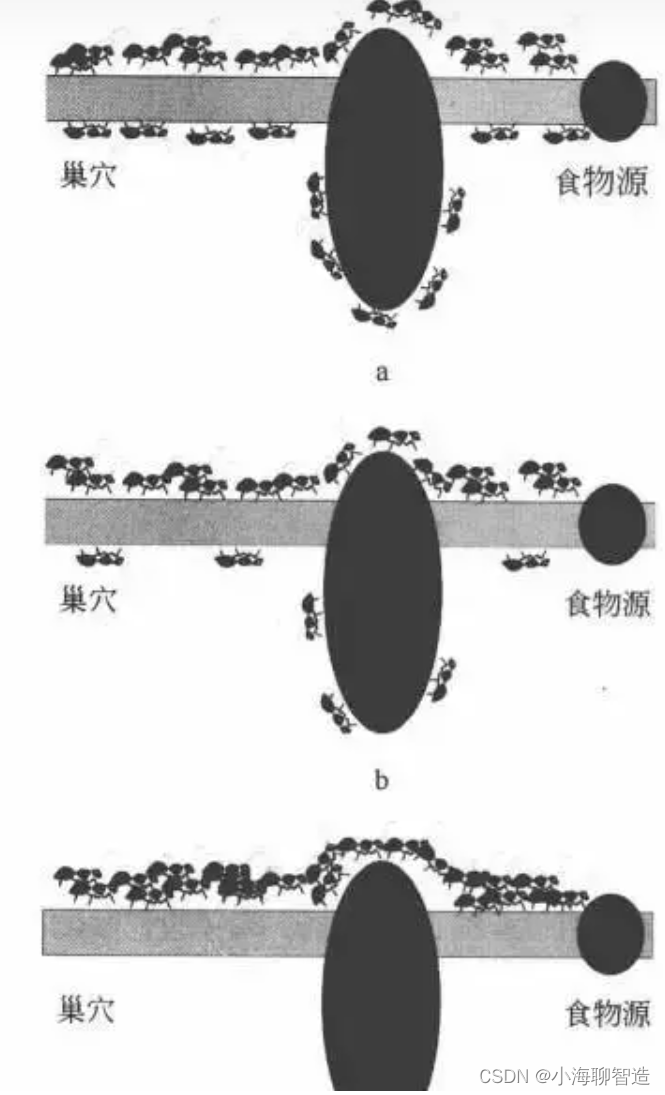
System(ACS))是由意大利学者Dorigo、Maniezzo等人于20世纪90年代首先提出来的。他们在研究蚂蚁觅食的过程中,发现蚁群整体会体现一些智能的行为,例如蚁群可以在不同的环境下,寻找最短到达食物源的路径。
后经进一步研究发现,这是因为蚂蚁会在其经过的路径上释放一种可以称之为“信息素(pheromone)”的物质,蚁群内的蚂蚁对“信息素”具有感知能力,它们会沿着“信息素”浓度较高路径行走,而每只路过的蚂蚁都会在路上留下“信息素”,这就形成一种类似正反馈的机制,这样经过一段时间后,整个蚁群就会沿着最短路径到达食物源了。
简单来说,就是走捷径!!!
上面的不太具体,看到另外一个博客说的挺 明了的,分享给同学们看看
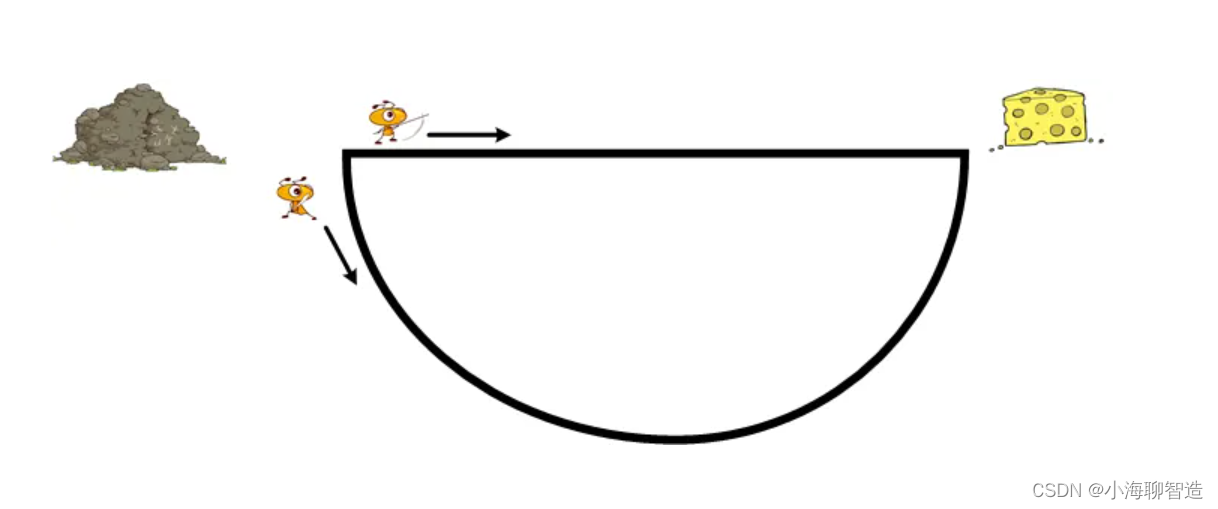
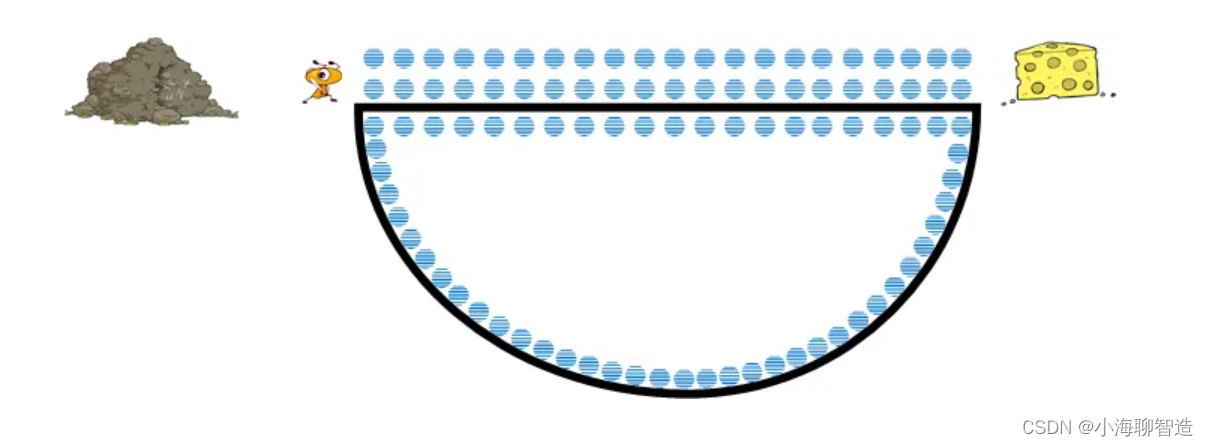
话说 有2个蚂蚁(分别叫小黄和大黄吧)出来找食物了。从洞穴出来,有两条路可以走,选择哪条路的概率是一致的,因为两条路目前都没有信息素。我们假设结果是大黄走了直线路,小黄走了曲线路。如下图:
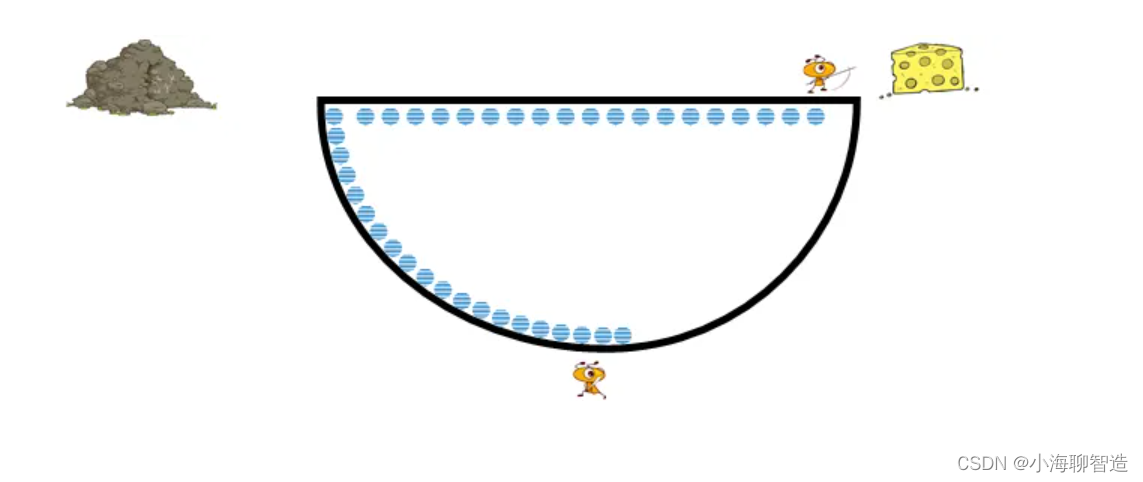
两个蚂蚁在行走过程中分泌信息素,用于标识路线。接着,过了一段时间,大黄 找到了奶酪,此时小黄还在行走中。如下图
接着大黄要回去的时候,由于直线路含有信息素而曲线路没有信息素(因为当前小黄还没走到奶酪附近),于是大黄选择走有信息素的道路也就是直线路。又过了一段时间,大黄回到了路的起点,而小黄刚走到奶酪附近。可以看出现在两条路的信息素浓度是2: 1。如图
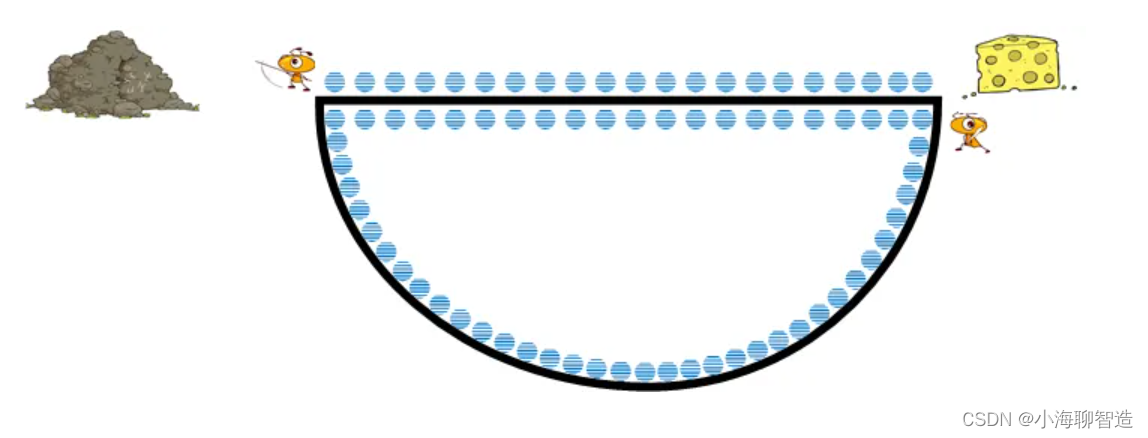
接着小黄要回去的时候,由于直线路含有的信息素浓度比曲线路高,于是小黄选择走有信息素浓度高的道路也就是直线路。最终当小黄也回到路的起点的时候,两条路的信息素浓度比例是3: 1,如下图
以后,每当有蚂蚁遇到起点岔路的时候,都会优先选择信息素浓度高的道路。这样,一大批的蚂蚁就能够准确的找到最短路径了。
蚁群算法演练
蚁群算法应用广泛,如旅行商问题(traveling salesman problem,简称TSP)、指派问题、Job-shop调度问题、车辆路径问题(vehicle routing problem)、图着色问题(graph coloring problem)和网络路由问题(network routing problem)等等,下面我们同之前推文一样,以TSP的求解为例演练蚁群算法的应用。
TSP问题描述
蚁群算法最早用来求解TSP问题,并且表现出了很大的优越性,因为它分布式特性,鲁棒性强并且容易与其它算法结合,但是同时也存在这收敛速度慢,容易陷入局部最优(local optimal)等缺点。
TSP问题(Travel Salesperson Problem,即旅行商问题或者称为中国邮递员问题),是一种,是一种NP-hard问题,此类问题用一般的算法是很大得到最优解的,所以一般需要借助一些启发式算法求解,例如遗传算法(GA),蚁群算法(ACO),微粒群算法(PSO)等等。
TSP问题可以分为两类,一类是对称TSP问题(Symmetric TSP),另一类是非对称问题(Asymmetric TSP)。所有的TSP问题都可以用一个图(Graph)来描述:
V = { c 1 , c 2 , … , c i , … , c n } , i = 1 , 2 , … , n V=\{c_1,c_2,\ldots,c_i,\ldots,c_n\},i=1,2,\ldots,n V={c1,c2,…,ci,…,cn},i=1,2,…,n是所有城市的集合.
c i c_i ci表示第i个城市, n n n为城市的数目;E = { ( r , s ) : r , s ∈ V } E=\{(r,s):r,s \in V\} E={(r,s):r,s∈V}是所有城市之间连接的集合;
C = { c r s : r , s ∈ V } C=\{c_{rs}:r,s \in V\} C={crs:r,s∈V}是所有城市之间连接的成本度量(一般为城市之间的距离);
如果 c r s = c s r c_{rs} = c_{sr} crs=csr, 那么该TSP问题为对称的,否则为非对称的。
一个TSP问题可以表达为:
求解遍历图 G = ( V , E , C ) G=(V,E,C) G=(V,E,C),所有的节点一次并且回到起始节点,使得连接这些节点的路径成本最低。
蚁群算法原理
假如蚁群中所有蚂蚁的数量为m,所有城市之间的信息素用矩阵pheromone表示,最短路径为bestLength,最佳路径为bestTour。每只蚂蚁都有自己的内存,内存中用一个禁忌表(Tabu)来存储该蚂蚁已经访问过的城市,表示其在以后的搜索中将不能访问这些城市;还有用另外一个允许访问的城市表(Allowed)来存储它还可以访问的城市;另外还用一个矩阵(Delta)来存储它在一个循环(或者迭代)中给所经过的路径释放的信息素;还有另外一些数据,例如一些控制参数 ( α , β , ρ , Q ) (\alpha,\beta,\rho,Q) (α,β,ρ,Q),该蚂蚁行走玩全程的总成本或距离(tourLength),等等。假定算法总共运行MAX_GEN次,运行时间为t。
蚁群算法计算过程如下:
(1)初始化
设t=0,初始化bestLength为一个非常大的数(正无穷),bestTour为空。初始化所有的蚂蚁的Delt矩阵所有元素初始化为0,Tabu表清空,Allowed表中加入所有的城市节点。随机选择它们的起始位置(也可以人工指定)。在Tabu中加入起始节点,Allowed中去掉该起始节点。
(2)为每只蚂蚁选择下一个节点。
为每只蚂蚁选择下一个节点,该节点只能从Allowed中以某种概率(公式1)搜索到,每搜到一个,就将该节点加入到Tabu中,并且从Allowed中删除该节点。该过程重复n-1次,直到所有的城市都遍历过一次。遍历完所有节点后,将起始节点加入到Tabu中。此时Tabu表元素数量为n+1(n为城市数量),Allowed元素数量为0。接下来按照(公式2)计算每个蚂蚁的Delta矩阵值。最后计算最佳路径,比较每个蚂蚁的路径成本,然后和bestLength比较,若它的路径成本比bestLength小,则将该值赋予bestLength,并且将其Tabu赋予BestTour。
其中 p i j ( t ) p_{ij}^{(t)} pij(t)表示选择城市j的概率, k k k表示第 k k k个蚂蚁, τ i j ( t ) \tau_{ij}^{(t)} τij(t)表示城市 i , j i,j i,j在第 t t t时刻的信息素浓度, η i j \eta_{ij} ηij表示从城市i到城市j的可见度,
η i j = 1 d i j \eta_{ij} = \frac 1 {d_{ij}} ηij=dij1, d i j d_{ij} dij表示城市 i , j i,j i,j之间的成本(或距离)。由此可见 d i j d_{ij} dij越小, η i j \eta_{ij} ηij越大,也就是从城市 i i i到 j j j的可见性就越大。 Δ τ i j k \Delta \tau_{ij}^k Δτijk表示蚂蚁 k k k在城市 i i i与 j j j之间留下的信息素。
L k L_k Lk表示蚂蚁 k k k经过一个循环(或迭代)锁经过路径的总成本(或距离),即tourLength. α , β , Q \alpha, \beta, Q α,β,Q 均为控制参数。
(3)更新信息素矩阵
令 t = t + n t=t+n t=t+nt,按照(公式3)更新信息素矩阵phermone。
[ \tau_{ij}(t+n) = \rho \cdot \tau_{ij}(t) + \Delta \tau_{ij} ]
(公式3)
τ i j ( t + n ) \tau_{ij}(t+n) τij(t+n)为 t + n t+n t+n时刻城市 i i i与 j j j之间的信息素浓度。 ρ \rho ρ为控制参数, D e l t a i j Delta_ij Deltaij为城市 i i i与 j j j之间信息素经过一个迭代后的增量。并且有
[ \Delta \tau_{ij} = \sum_{k=1}^m \Delta \tau_{ij}^k]
(公式4)
其中 Δ τ i j k \Delta \tau_{ij}^k Δτijk由公式计算得到。
(4)检查终止条件
如果达到最大代数MAX_GEN,算法终止,转到第(5)步;否则,重新初始化所有的蚂蚁的Delt矩阵所有元素初始化为0,Tabu表清空,Allowed表中加入所有的城市节点。随机选择它们的起始位置(也可以人工指定)。在Tabu中加入起始节点,Allowed中去掉该起始节点,重复执行(2),(3),(4)步。
(5)输出最优值
java 代码实现
//创建一个蚂蚁类 Ant.java
public class Ant {
private List<Integer> route = new ArrayList<Integer>(); //路线:记录蚂蚁行走的路线
private Integer currentCity; //当前城市:记录蚂蚁当前所在城市的ID
private List<Integer> citys = new ArrayList<Integer>(); //城市:记录需要行走的城市ID
private double[][] pheromoneMatrix; //信息素矩阵
private int[][] distanceMatrix; //距离矩阵(整型方便查看)
//构造器
public Ant(List<Integer> citys, double[][] pheromoneMatrix, int[][] distanceMatrix) {
this.citys = citys;
this.pheromoneMatrix = pheromoneMatrix;
this.distanceMatrix = distanceMatrix;
}
/**
* 添加路线
* @param cityId
*/
private void addRoute(Integer cityId) {
route.add(cityId); //路线中添加城市ID
currentCity = cityId; //当前城市修改为城市ID
citys.remove(cityId); //需要行走的城市移除当前城市ID
}
/**
* 随机选择初始城市
*/
private void randomSelectCity() {
Random random = new Random();
Integer cityId = random.nextInt(citys.size())+1;
addRoute(cityId);
}
/**
* 选择下一个城市
*/
private void selectNextCity() {
if(citys.size() == 1) {
addRoute(citys.get(0));
addRoute(route.get(0)); //路线添加最开始的城市
return;
}
Double alpha = 1.0; //信息素因子权重
Double beta = 2.0; //路线距离权重
Map<Integer, Double> molecules = new HashMap<Integer, Double>();
//计算选路概率公式中的分子
for (Integer city : citys) {
//城市从1开始数,数组从0开始数,所以涉及数组都要‘-1’
Double molecule = Math.pow(pheromoneMatrix[currentCity-1][city-1], alpha) * Math.pow(1.0 / distanceMatrix[currentCity-1][city-1], beta);
molecules.put(city, molecule);
}
//计算选路概率公式中的分母
Double totalMolecule = 0.0;
for(Integer city : molecules.keySet()) {
totalMolecule += molecules.get(city);
}
//轮盘赌选择下一个城市
double random = Math.random();
Double temp = 0.0;
for(Integer city : molecules.keySet()) {
temp += molecules.get(city) / totalMolecule;
if(temp >= random) {
addRoute(city);
break;
}
}
}
/**
* 蚂蚁开始旅行所有城市
*/
public void tour() {
int cityQuantity = citys.size();
randomSelectCity();
for(int i=0; i<cityQuantity; i++) {
selectNextCity();
}
}
/**
* 获取路线
* @return
*/
public List<Integer> getRoute() {
return route;
}
/**
* 计算路线总距离
* @return
*/
public Integer getRouteLength() {
Integer length = 0;
for(int i=0; i<route.size()-1; i++) {
length += distanceMatrix[route.get(i)-1][route.get(i+1)-1];
}
return length;
}
}
//创建一个AOC类:是蚁群优化算法主要实现类
public class ACO {
List<Integer> citys = new ArrayList<Integer>(); //城市集合
private double[][] pheromoneMatrix; //信息素矩阵
private int[][] distanceMatrix; //距离矩阵
private int times; //运行次数
private int antQuantity; // 蚂蚁数量
private List<Integer> bestRoute; //最佳路线
private Integer bestLength = -1; //最佳距离
//构造器
public ACO(List<Integer> citys, double[][] pheromoneMatrix, int[][] distanceMatrix, int times, int antQuantity) {
this.citys = citys;
this.pheromoneMatrix = pheromoneMatrix;
this.distanceMatrix = distanceMatrix;
this.times = times;
this.antQuantity = antQuantity;
}
/**
* 更新信息素
* @param ants 蚂蚁群
*/
private void update(List<Ant> ants) {
//信息素挥发
double volatilizationRate = 0.5; //挥发率
for(int i=0; i<citys.size(); i++) {
for(int j=0; j<citys.size(); j++) {
pheromoneMatrix[i][j] = pheromoneMatrix[i][j] * (1.0-volatilizationRate);
}
}
//信息素新增
for(Ant ant : ants) {
List<Integer> route = ant.getRoute();
for(int i=0; i<route.size()-1; i++){
pheromoneMatrix[route.get(i)-1][route.get(i+1)-1] += 1.0 / ant.getRouteLength();
}
}
}
/**
* 记录最佳路径和最佳距离
*/
private void recordBest(List<Ant> ants) {
//给bestLength赋予初始值
if(bestLength == -1.0) {
bestLength = ants.get(0).getRouteLength();
bestRoute = ants.get(0).getRoute();
}
//遍历比较最佳
for(Ant ant : ants) {
if(bestLength > ant.getRouteLength()) {
bestLength = ant.getRouteLength();
bestRoute = ant.getRoute();
}
}
}
/**
* 运行蚁群优化算法
*/
private void runAlgorithm(){
//创建蚂蚁集合存储蚂蚁
List<Ant> ants = new ArrayList<Ant>();
for(int i=0; i<antQuantity; i++){
//复制城市集合(集合为地址引用,为了不影响原参数,复制一个新集合)
List<Integer> cityCopy = new ArrayList<Integer>();
for (Integer city : citys) {
cityCopy.add(city);
}
//创建蚂蚁,并开始旅行所有城市
Ant ant = new Ant(cityCopy, pheromoneMatrix, distanceMatrix);
ant.tour();
ants.add(ant);
}
update(ants); //更新信息素
recordBest(ants); //记录最佳路线与距离
}
/**
* 多次运行蚁群优化算法(蚂蚁算法的运行入口)
*/
public void run() {
for(int i=0; i<times; i++){
runAlgorithm();
}
}
/**
* 获取最佳路线
*/
public List<Integer> getBestRoute() {
return bestRoute;
}
/**
* 获取最佳距离
*/
public Integer getBestLength() {
return bestLength;
}
}
- 针对TSP问题的蚂蚁优化算法就写好了,只要创建AOC,传入对应的参数,运行run()方法就会跑起来,通过getXxxx获取路线以及路线长度
//主程序代码演示
public class Main {
public static void main(String[] args) {
//自定义距离矩阵
int[][] distanceMatrix = new int[][]{{0, 1, 3, 1}, {1, 0, 3, 2}, {3, 3, 0, 2}, {1, 2, 2, 0}};
//创建信息素矩阵并赋初值
double[][] pheromoneMatrix = new double[4][4];
for(int i=0; i<distanceMatrix.length; i++) {
for(int j=0; j<distanceMatrix.length; j++) {
pheromoneMatrix[i][j] = 0.1;
}
}
//创建城市集合
List<Integer> citys = new ArrayList<Integer>();
for(int i=0; i<4; i++) {
citys.add(i+1);
}
//运行蚁群优化算法
ACO aco = new ACO(citys, pheromoneMatrix, distanceMatrix, 50, 6);
aco.run();
System.out.println(aco.getBestRoute());
System.out.println(aco.getBestLength());
}
}
2.3 自定义工具类
-
由于自己定义距离矩阵,信息素矩阵觉得麻烦,就创建一个工具类实现创建
-
(1)将城市信息存储在一个txt文件中
- 城市ID X轴 Y轴
1 6734 1453
2 2233 10
3 5530 1424
4 401 841
5 3082 1644
6 7608 4458
7 7573 3716
8 7265 1268
9 6898 1885
10 1112 2049
11 5468 2606
12 5989 2873
13 4706 2674
14 4612 2035
15 6347 2683
16 6107 669
17 7611 5184
18 7462 3590
19 7732 4723
20 5900 3561
21 4483 3369
22 6101 1110
23 5199 2182
24 1633 2809
25 4307 2322
26 675 1006
27 7555 4819
28 7541 3981
29 3177 756
30 7352 4506
31 7545 2801
32 3245 3305
33 6426 3173
34 4608 1198
35 23 2216
36 7248 3779
37 7762 4595
38 7392 2244
39 3484 2829
40 6271 2135
41 4985 140
42 1916 1569
43 7280 4899
44 7509 3239
45 10 2676
46 6807 2993
47 5185 3258
48 3023 1942
- (2)创建工具类来读取txt信息
public class Utils {
/**
* 读取文件内容,将每一行文本封装为字符串集合
* @return
* @throws Exception
*/
private static List<String> readFile(){
//文件路径,按照自己情况进行修改
String filePath = "D://data//position.txt";
List<String> texts = null;
BufferedReader br = null;
//异常处理
try {
br = new BufferedReader(new InputStreamReader(new FileInputStream(filePath))); //创建读取文件流
texts = new ArrayList<String>(); //创建集合存储字符串
while(true) {
String text = br.readLine();
if(text == null) { //直到下一行没有内容,退出循环
break;
}
texts.add(text);
}
} catch (IOException e) {
e.printStackTrace();
} finally {
try {
br.close();
} catch (IOException e) {
e.printStackTrace();
}
}
return texts;
}
/**
* 创建城市Id集合
* @return
*/
public static List<Integer> getCitys() {
Integer cityQuantity = Integer.valueOf(readFile().get(0));
List<Integer> citys = new ArrayList<Integer>();
for(int i=0; i<cityQuantity; i++) {
citys.add(i+1);
}
return citys;
}
/**
* 创建距离矩阵
* @return
*/
public static int[][] getDistanceMatrix() {
List<String> texts = readFile();
Integer cityQuantity = Integer.valueOf(texts.get(0));
int[][] distanceMatrix = new int[cityQuantity][cityQuantity];
for(int i=0; i<cityQuantity; i++) {
distanceMatrix[i][i] = 0;
for (int j=i+1; j<cityQuantity; j++) {
//按空格分割字符串
String[] city1 = texts.get(i + 1).split(" ");
String[] city2 = texts.get(j + 1).split(" ");
//两点距离公式(整数方便查看)
double distance = Math.pow((Integer.valueOf(city1[1]) - Integer.valueOf(city2[1])), 2) + Math.pow((Integer.valueOf(city1[2]) - Integer.valueOf(city2[2])), 2);
distanceMatrix[i][j] = (int) Math.sqrt(distance);
distanceMatrix[j][i] = distanceMatrix[i][j];
}
}
return distanceMatrix;
}
/**
* 初始化信息素矩阵
* @param value 初始值
* @return
*/
public static double[][] getPheromoneMatrix(double value) {
Integer cityQuantity = Integer.valueOf(readFile().get(0));
double[][] pheromoneMatrix = new double[cityQuantity][cityQuantity];
for(int i=0; i<cityQuantity; i++) {
for(int j=0; j<cityQuantity; j++) {
pheromoneMatrix[i][j] = value; //赋予初始信息素值
}
}
return pheromoneMatrix;
}
}
- (3)通过使用工具类的主程序
public class Main {
public static void main(String[] args) {
List<Integer> citys = Utils.getCitys(); //城市集合
double[][] pheromoneMatrix = Utils.getPheromoneMatrix(1.0); //信息素矩阵
int[][] distanceMatrix = Utils.getDistanceMatrix(); //距离矩阵
ACO aco = new ACO(citys, pheromoneMatrix, distanceMatrix, 150, 72);
aco.run();
System.out.println(aco.getBestRoute());
System.out.println(aco.getBestLength());
}
}
运行结果:
// 获取最佳路线
[25, 14, 23, 11, 12, 15, 40, 9, 1, 8, 38, 31, 44, 18, 7, 28, 36, 30, 6, 37, 19, 27, 43, 17, 46, 33, 20, 47, 21, 13, 3, 22, 16, 41, 34, 5, 48, 29, 2, 42, 10, 26, 4, 35, 45, 24, 32, 39, 25]
//获取最佳距离
35700