Savitzky-Golay filter design

The SAVGOL function returns the coefficients of a Savitzky-Golay smoothing filter, which can then be applied using the CONVOL function. The Savitzky-Golay smoothing filter, also known as least squares or DISPO (digital smoothing polynomial), can be used to smooth a noisy signal.

The filter is defined as a weighted moving average with weighting given as a polynomial of a certain degree. The returned coefficients, when applied to a signal, perform a polynomial least-squares fit within the filter window. This polynomial is designed to preserve higher moments within the data and reduce the bias introduced by the filter. The filter can use any number of points for this weighted average.

Syntax

b = sgolay(order,framelen) b = sgolay(order,framelen,weights) [b,g] = sgolay(...)

Description

b = sgolay(order,framelen) designs a Savitzky-Golay FIR smoothing filter with polynomial order order and frame length framelen. order must be less than framelen, and framelen must be odd. If order = framelen-1, the designed filter produces no smoothing.

The output, b, is a framelen-by-framelen matrix whose rows represent the time-varying FIR filter coefficients. In a smoothing filter implementation (for example, sgolayfilt), the last (framelen-1)/2 rows (each an FIR filter) are applied to the signal during the startup transient, and the first (framelen-1)/2 rows are applied to the signal during the terminal transient. The center row is applied to the signal in the steady state.

b = sgolay(order,framelen,weights) specifies a weighting vector, weights, with length framelen, which contains the real, positive-valued weights to be used during the least-squares minimization.

[b,g] = sgolay(...) returns the matrix g of differentiation filters. Each column of g is a differentiation filter for derivatives of order p-1, where p is the column index. Given a signal x of length framelen, you can find an estimate of the pth order derivative, xp, of its middle value from

xp((framelen+1)/2) = (factorial(p)) * g(:,p+1)' * x

例子

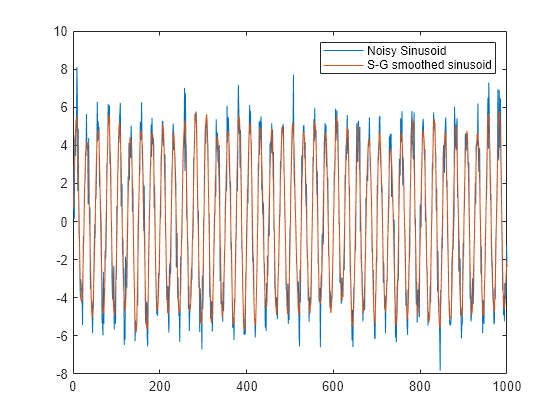
dt = 1/5;
t = (0:dt:200-dt)';

x = 5*sin(2*pi*0.2*t) + randn(size(t));

Use sgolay to smooth the signal. Use 21-sample frames and 4th-order polynomials.

order = 4;
framelen = 21;

b = sgolay(order,framelen);

Compute the steady-state portion of the signal by convolving it with the center row of b.

ycenter = conv(x,b((framelen+1)/2,:),'valid');

Compute the transients. Use the last rows of b for the startup and the first rows of b for the terminal.

ybegin = b(end:-1:(framelen+3)/2,:) * x(framelen:-1:1);
yend = b((framelen-1)/2:-1:1,:) * x(end:-1:end-(framelen-1));

Concatenate the transients and the steady-state portion to generate the complete smoothed signal. Plot the original signal and the Savitzky-Golay estimate.

y = [ybegin; ycenter; yend];
plot([x y])
legend('Noisy Sinusoid','S-G smoothed sinusoid')