Bootstrap

【初阶数据结构和算法】二叉树顺序结构---堆的定义与实现(附源码)

在这里插入图片描述

文章目录

一、堆的定义与结构

   本篇内容与树和二叉树的知识相关，如果还不了解什么是树，什么是二叉树，那么可以先看这篇文章了解树和二叉树的基础知识：【初阶数据结构和算法】初识树与二叉树的概念以及堆和完全二叉树之间的关系
   堆的本质是一颗完全二叉树，只是它的要求比完全二叉树更加严格，它要求每颗子树的根节点都是当前子树的最大值或最小值，当根节点是最大值时，它就是一个大根堆，当根节点是最小值时，它就是一个小根堆
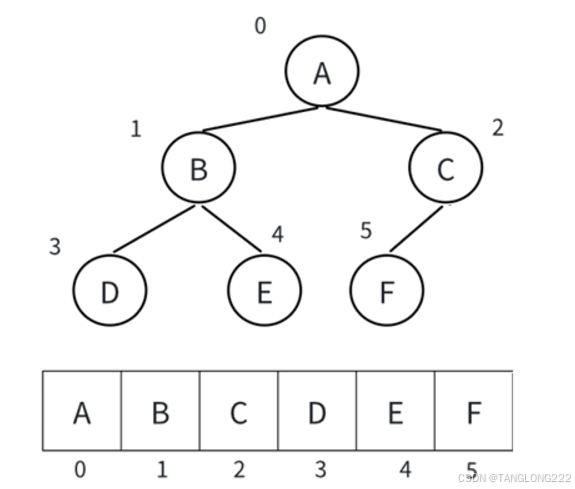
   在上篇文章中我们也提到了，存储完全二叉树可以使用数组，存储非完全二叉树可以使用链表，而堆就是一种特殊的完全二叉树，所以堆的存储我们就使用数组，也就是顺序表的形式，如图：
在这里插入图片描述

   我们将堆这个完全二叉树从上至下，从左至右的数据存放在数组中，至于怎么保证它每颗子树的根节点都是当前子树的最大值或最小值，我们在入堆和出堆的位置细讲，而顺序表的结构我们已经很熟悉了，这里直接写出来：

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* arr;
	int size;
	int capacity;
}HP;

二、堆的实现

1.堆的初始化和销毁

   堆的初始化和销毁与顺序表的初始化和销毁一致，这里我们只简单提一下

堆的初始化

   堆的初始化就是将数组置空，有效数据个数和容量大小置0，如下：

//堆的初始化
void HPInit(HP* php)
{
	assert(php);
	php->arr = NULL;
	php->size = php->capacity = 0;
}

堆的销毁

   堆的销毁就是先判断数组是否为空，不为空就将它释放掉，因为数组的空间是我们向操作系统申请来的，不会主动释放，如果我们不主动释放就会造成内存泄漏，最后我们将数组置空，有效数据个数和容量大小置0，如下：

//堆的销毁
void HPDestroy(HP* php)
{
	assert(php);
	if (php->arr)
		free(php->arr);
	php->arr = NULL;
	php->size = php->capacity = 0;
}

2.向上调整算法和入堆

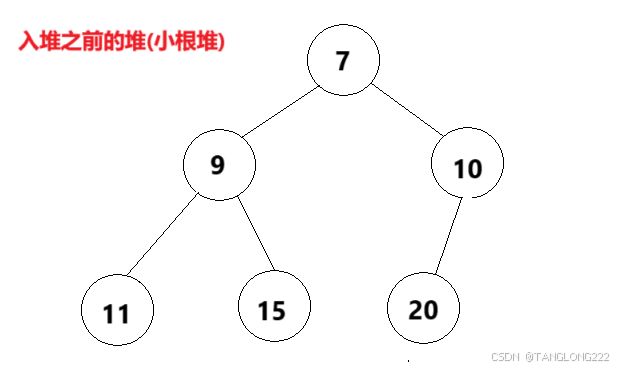
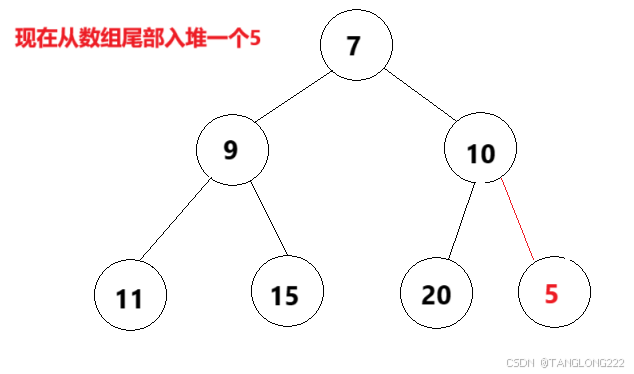
   接下来就是入堆操作，也就是向堆中插入数据，但是我们要知道，一般往数组中插入数据都是向数组尾部插入，那么是不是就会出现，原本堆的每颗子树的根节点都是当前子树的最大值或最小值，但是从尾部插入数据后会打破这个平衡，如图：
在这里插入图片描述

在这里插入图片描述

   可以看到，原本的堆是一个小根堆，但是我们插入一个5之后，它就不构成小根堆了，这个时候就要用到我们的向上调整算法，当然，如果插入一个数据后还依然构成小根堆的话，我们就不做处理即可

向上调整算法

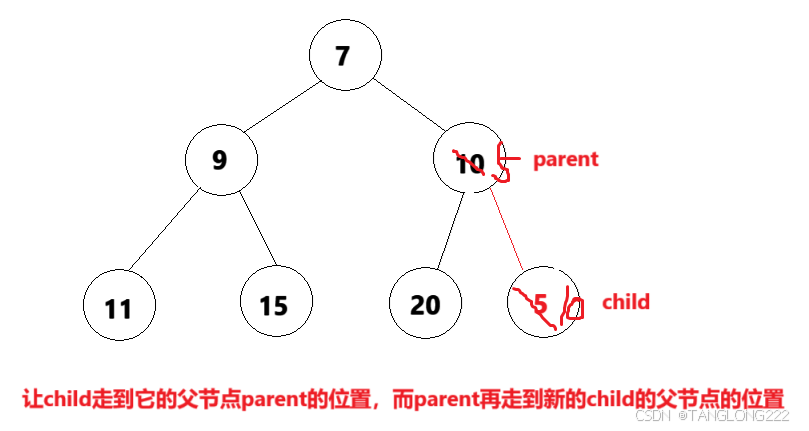
   在讲解向上调整算法时，我们就统一以小根堆为例，向上调整算法的本质就是将我们插入的数据当作孩子节点，让它和它的父节点进行比较
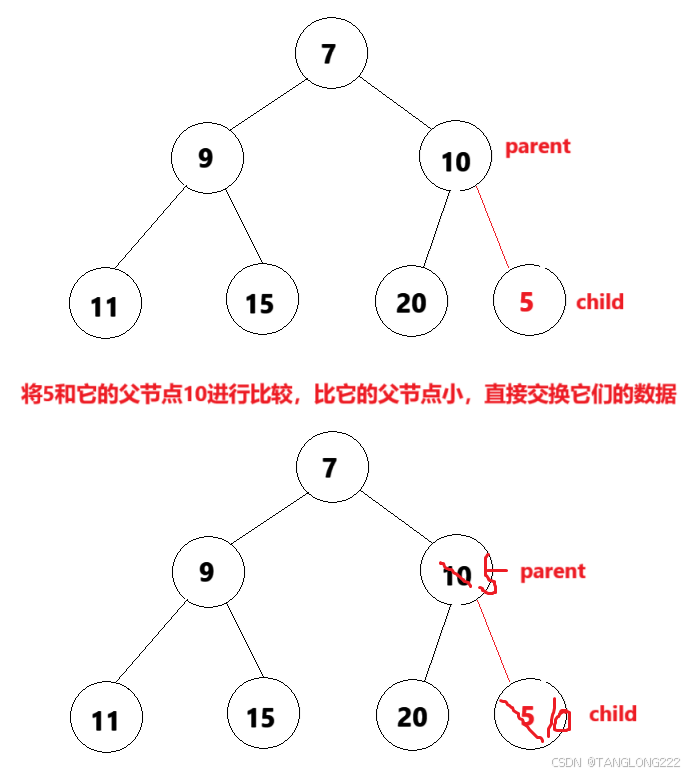
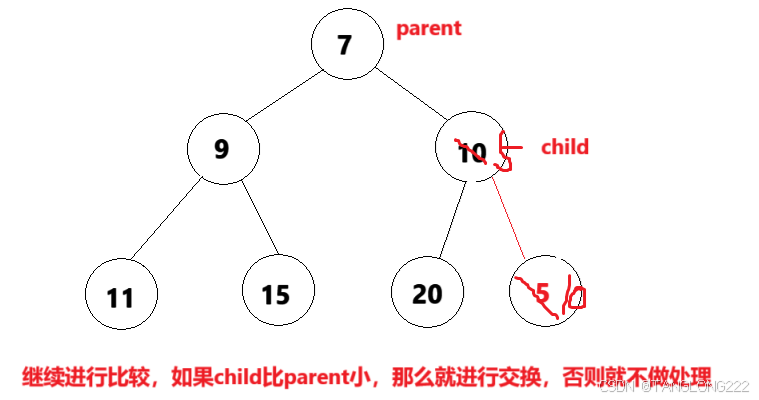
   那么有了孩子节点，怎么找到父节点呢？其实我们在上一篇讲过，父节点parent的下标等于(child-1)/2，找到父节点后，我们就看插入的数据是不是比它的父节点还小，如果是那么就直接进行交换，否则就不做操作，如图：
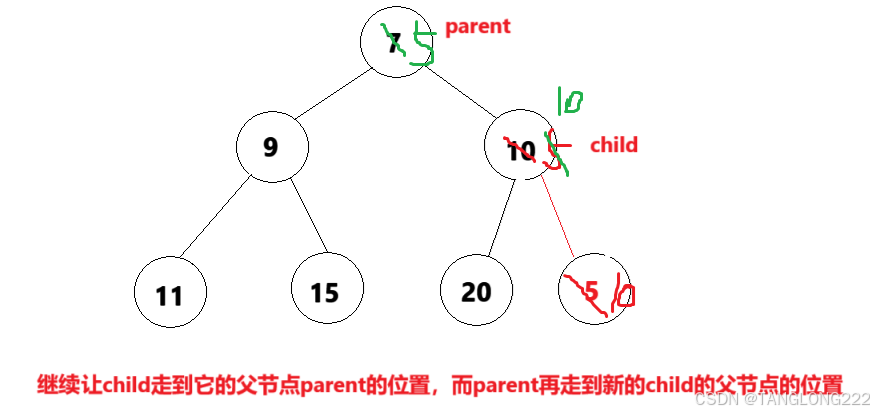
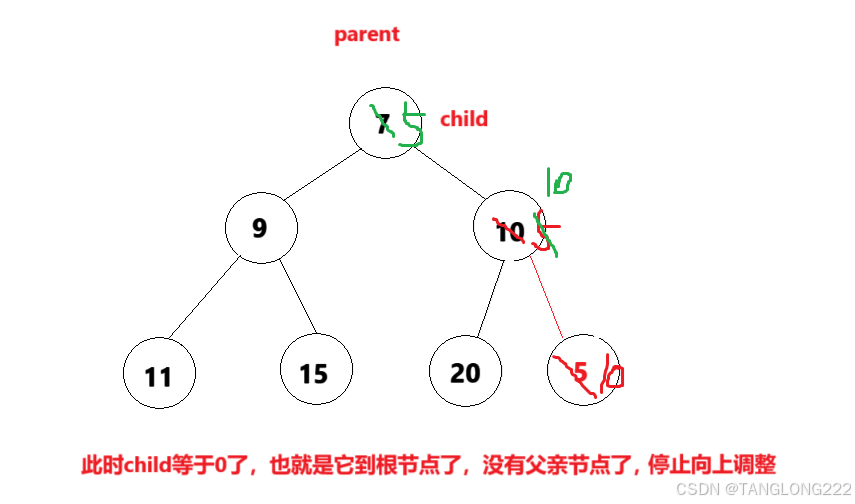
在这里插入图片描述
   但是我们发现交换一次后还是没有构成小根堆，所以向上调整算法要求，只要我们做了交换，那么就让child走到parent，parent再走到新的child的父节点，继续进行比较，直到child为0，此时它就没有父亲节点了，停止向上调整，如图：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
   可能光说有点不理解，但是我们画图之后思路就很清晰了，接下来我们就开始按照上面的思路将代码写出来，如下：

//向上调整
void AdjustUp(HPDataType* arr, int child)
{
    //根据传来的孩子节点找到父节点
	int parent = (child - 1) / 2;
	//只要child不为0就一直循环
	while (child > 0)
	{
	    //如果孩子比父亲小就进行交换
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			//让孩子节点走到父亲节点的位置
			child = parent;
			//让父亲节点走到新的孩子节点的父节点
			parent = (child - 1) / 2;
		}
	//孩子不比父亲小，那么说明此时已经成堆了，直接跳出循环
		else
		{
			break;
		}
	}
}

   在上面我们演示的是一个小根堆的写法，就是比较孩子和父亲谁小，如果我们要构建一个大根堆，就要比较孩子和父亲谁大，只需要将比较时的小于改成大于即可

入堆

   有了向上调整算法我们入堆就很简单了，只需要将数据插入到数组最后，然后调用向上调整函数，就可以让我们的堆不被打乱
   但是我们同时要注意，插入数据之前要检查数组空间大小是否足够，如果不够的话要进行扩容，如下：

//入堆
void HPPush(HP* php, HPDataType x)
{
	assert(php);
	//检查空间是否足够
	if (php->size == php->capacity)
	{
		php->capacity = php->capacity == 0 ? 4 : 2 * php->capacity;
		HPDataType* tmp = (HPDataType*)realloc(php->arr, php->capacity * sizeof(HPDataType));
		if (tmp == NULL)
		{
			perror("realloc");
			return;
		}
		php->arr = tmp;
	}
	//插入数据
	php->arr[php->size] = x;
	//调用向上调整算法
	AdjustUp(php->arr, php->size);
	php->size++;
}

3.向下调整算法和出堆顶数据

   在正式了解向下调整算法和出堆顶数据之前，首先我们要知道堆删除数据是删除堆顶的数据，也就是下标为0的数据，因为堆顶的数据是最特殊的，它是整个堆最大或最小的值，我们在堆的应用会讲到它的用法
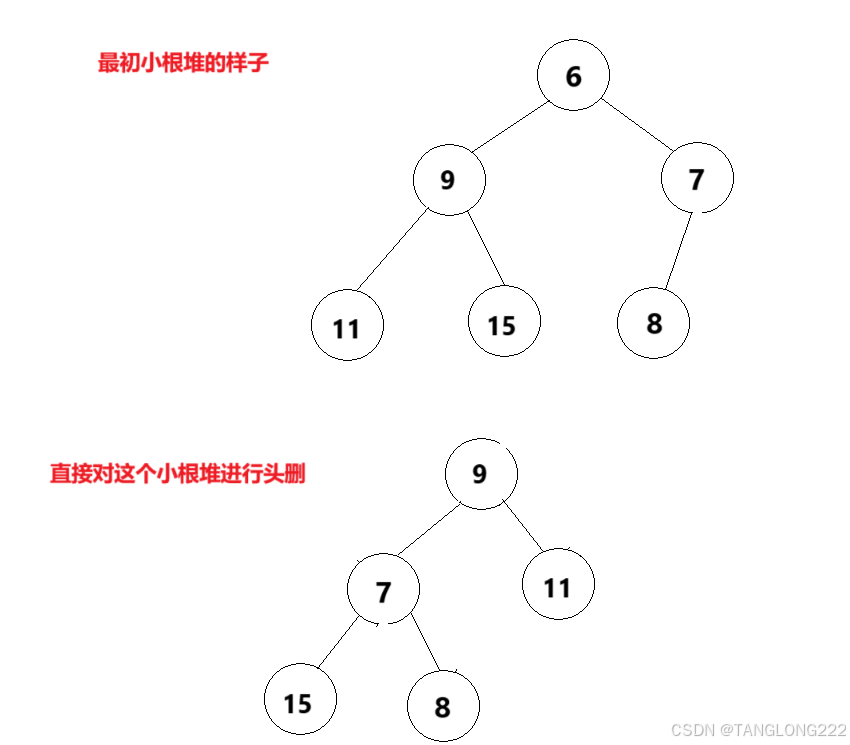
   那么了解了这一点之后，我们再来想想怎么删除堆顶数据，如果直接头删的话，那么之前堆的结构会完全乱套，我们画个图就知道了，以小根堆为例，如下：
在这里插入图片描述
   可以看到如果我们直接对堆进行头删的话，整个堆的数据都被打乱了，结构也变乱了，我们要调整的话也无从下手，接下来我们就来介绍删除堆顶数据的正确做法
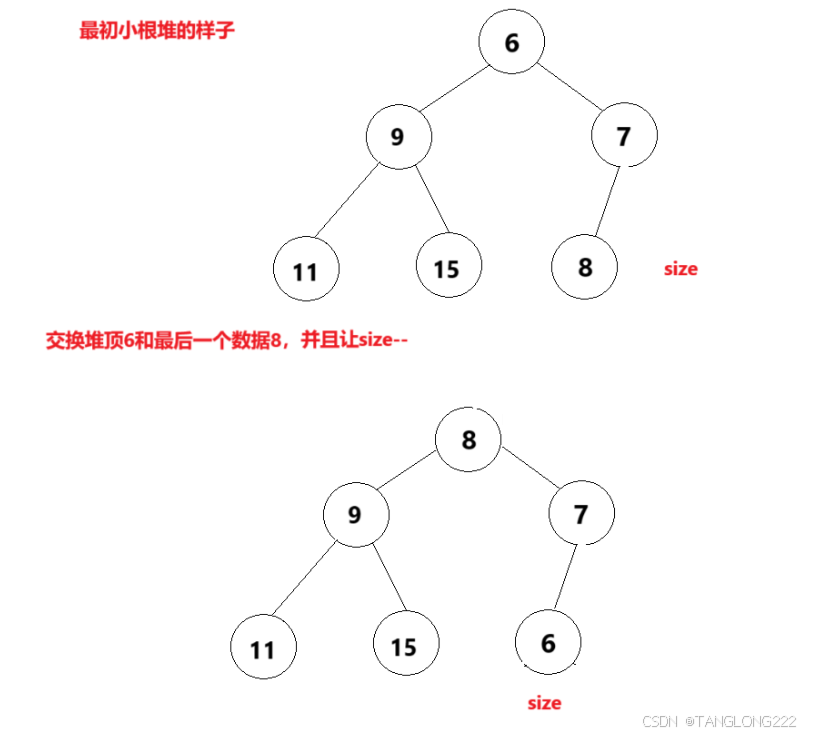
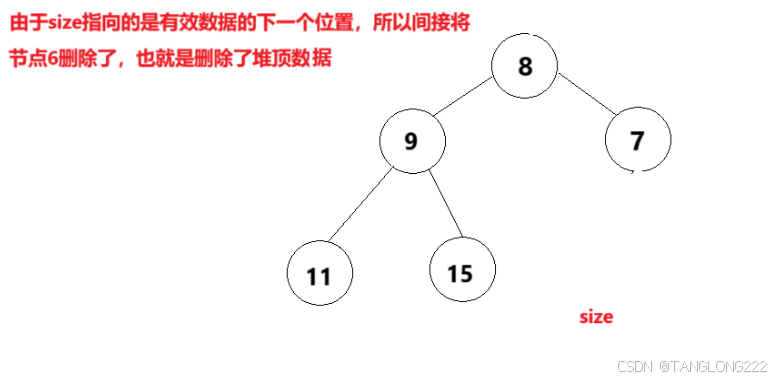
   删除堆顶数据的正确做法就是，交换最后一个数据和堆顶数据，然后让size- -，这样我们就只会影响最后一个数据和堆顶数据，不会影响其它节点，如图：
在这里插入图片描述
在这里插入图片描述
   经过上面的操作，我们就可以发现，我们删除了堆顶数据，只是说将堆中的最后一个数据移到了堆顶，但是也只改变了堆中的最后一个数据的位置，不至于像头删那样将整个堆的结构打乱
   那么将堆中的最后一个数据放到了堆顶，此时堆很可能不是一个有效的堆，所以我们需要从堆顶向下调整整个堆，我们需要一个向下调整算法

向下调整算法

   经过上面的分析，我们知道堆删除数据后，堆顶元素可能不符合堆的要求，所以我们要从堆顶开始向下调整，要注意的是，我们举例都是以小根堆为例
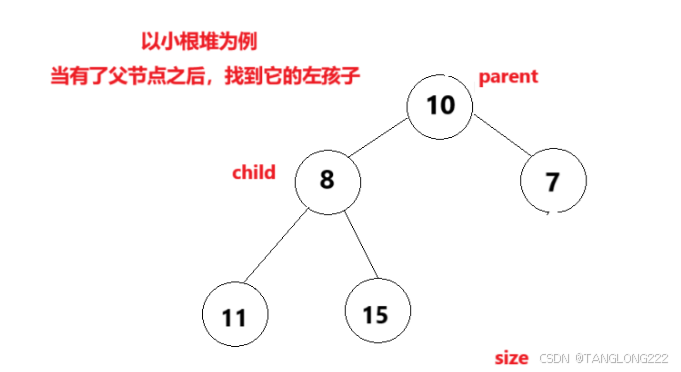
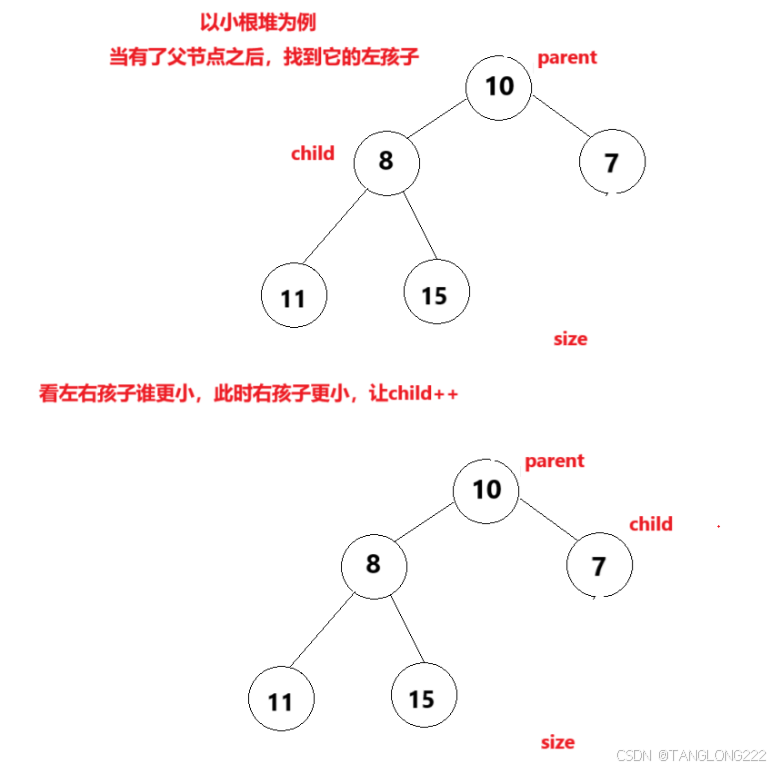
   具体方法就是，将堆顶当作父节点parent，根据2*parent找到它的孩子节点child，最后让父节点和孩子节点进行比较，如果孩子节点更小就进行交换，然后让父亲走到孩子的位置，孩子再走到新父亲的孩子节点
   如果孩子节点比父节点更大的话就不做修改，跟我们的向上调整算法类似，但是我们要注意一个点，我们在向下调整的时候，需要看当前父节点的左孩子和右孩子谁小，父节点要和小的那个孩子进行交换，为什么呢？
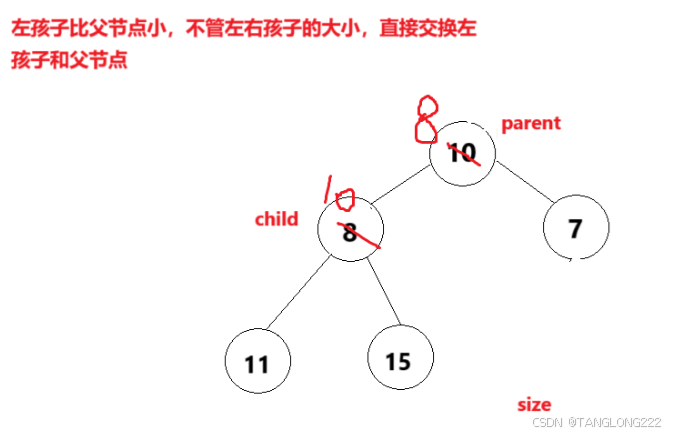
   因为如果父节点和较大的那个孩子进行交换的话，较大的那个孩子就成了堆顶，另一个较小的孩子就比堆顶小，不满足小根堆的条件，如图：
在这里插入图片描述
在这里插入图片描述
   可以发现，在这种情况下，我们经过交换后并不符合堆的要求，因为原本的右孩子较小，但是父节点是和左孩子进行交换的，导致较大的左孩子到了堆顶，不符合堆的要求
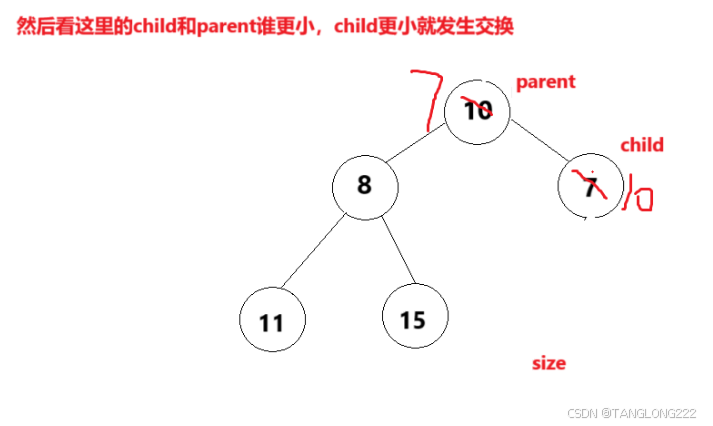
   所以我们在进行向下调整时，找到左孩子child后，还要先判断一下左右孩子谁更小，如果左孩子更小就不需要做更改，如果右孩子更小就让child++，这样就可以让child走到更小的右孩子了(注意左右孩子的关系，右孩子比左孩子的下标大1)
   那么有了正确的思路之后我们重新走一遍上面的过程，看看有没有问题，如图：
在这里插入图片描述
在这里插入图片描述
   那么有了上图的思路，我们直接根据思路写出对应的代码即可，如下：

//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{
    //根据给出的孩子父节点算出对应的左孩子
	int child = parent * 2 + 1;
	//如果child没有越界就持续向下调整
	while (child < n)
	{
	    //如果右孩子存在并且更小，就让child++走到更小的右孩子上
		if (child + 1 < n && arr[child + 1] < arr[child])
		{
			child++;
		}
		//如果孩子比父亲更小就进行交换
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]); 
			//交换完之后parent重新走到child的位置
			//child走到新parent的左孩子位置
			parent = child;
			child = parent * 2 + 1;
		}
		//如果较小的孩子都比父节点大
		//说明调整完毕，退出循环
		else
		{
			break;
		}
	}
}

出堆

   上面我们其实已经完整讲解了出堆的过程，这里我们再次回顾一下，出堆就是指删除堆中的堆顶数据，方法就是交换堆顶和最后一个数据，让size- -，间接删除了堆顶数据，然后最后一个数据到了堆顶，再对它进行向下调整即可
   那么有了思路我们就可以直接写代码了，如下：

//出堆顶元素
void HPPop(HP* php)
{
	assert(php);
	php->size--;
	Swap(&php->arr[0], &php->arr[php->size]);
	AdjustDown(php->arr, 0, php->size);
}

4.堆的有效数据个数和判空

堆的有效数据个数

   堆的有效数据个数由size记录，直接返回size即可，如下：

//堆的有效数据个数
int HPSize(HP* php)
{
	assert(php);
	return php->size;
}

堆的判空

   堆的判空就是判断堆的有效数据个数是否为0，也是跟size相关，如下：

//堆的判空
bool HPEmpty(HP* php)
{
	return php->size == 0;
}

5.取堆顶数据

   取堆顶数据就是取堆中下标为0位置的数据，如下：

//取堆顶数据
HPDataType HPTop(HP* php)
{
	assert(php);
	return php->arr[0];
}

三、堆的源码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* arr;
	int size;
	int capacity;
}HP;

//堆的初始化
void HPInit(HP* php)
{
	assert(php);
	php->arr = NULL;
	php->size = php->capacity = 0;
}

//堆的销毁
void HPDestroy(HP* php)
{
	assert(php);
	if (php->arr)
		free(php->arr);
	php->arr = NULL;
	php->size = php->capacity = 0;
}

//交换函数
void Swap(HPDataType* x, HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}

//向上调整
void AdjustUp(HPDataType* arr, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}

	}
}

//入堆
void HPPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		php->capacity = php->capacity == 0 ? 4 : 2 * php->capacity;
		HPDataType* tmp = (HPDataType*)realloc(php->arr, php->capacity * sizeof(HPDataType));
		if (tmp == NULL)
		{
			perror("realloc");
			return;
		}
		php->arr = tmp;
	}
	php->arr[php->size] = x;
	AdjustUp(php->arr, php->size);
	php->size++;
}

//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && arr[child + 1] < arr[child])
		{
			child++;
		}
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]); 
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//出堆顶元素
void HPPop(HP* php)
{
	assert(php);
	php->size--;
	Swap(&php->arr[0], &php->arr[php->size]);
	AdjustDown(php->arr, 0, php->size);
}

//取堆顶数据
HPDataType HPTop(HP* php)
{
	assert(php);
	return php->arr[0];
}

//堆的有效数据个数
int HPSize(HP* php)
{
	assert(php);
	return php->size;
}

//堆的判空
bool HPEmpty(HP* php)
{
	return php->size == 0;
}

   今天堆的分享就到这里啦，有什么疑问欢迎私信，下一篇文章我们就开始介绍二叉树链式结构了，感受递归的暴力美学，敬请期待吧！
   bye~

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
网关的鉴权功能设计思考
SpringMVC的核心组件及工作流程
带你了解线程池的创建和使用
java实现心形图
应对“微软蓝屏”的个人看法
2024年前端开发趋势的 6 个框架
java拼图小游戏
最新ChatGPT网站源码/支持用户注册付费套餐/支持Ai绘画/支持用户会员套餐/邀请分佣功能/支持后台一键更新/网站后台管理/永久更新
计算机毕业设计必看必学16640基于BS架构的图书管理系统的设计与实现原创定制程序,java、PHP、python、小程序、文案全套、毕设成品等
酒店管理系统的设计与实现（任务书+中期检查+PPT+论文）
;