一、二叉树的遍历
在链式二叉树的定义与实现中我们已经详细讲解了二叉树常见的三种遍历方式,以及层序遍历,这里给出链接:【初阶数据结构与算法】二叉树链式结构的定义与实现万字笔记(附源码)
放在这里是希望大家可以通过题目链接去练习一下,看看自己能不能写出来,写不出来再去上文复习复习,链接如下:
前序遍历:https://leetcode.cn/problems/binary-tree-preorder-traversal/description/
中序遍历:https://leetcode.cn/problems/binary-tree-inorder-traversal/description/
后序遍历:https://leetcode.cn/problems/binary-tree-postorder-traversal/description/
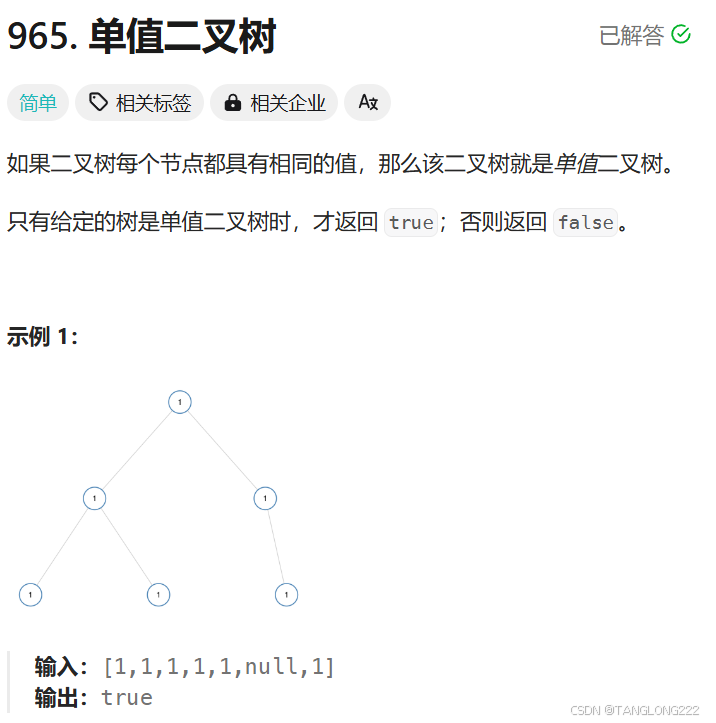
二、单值二叉树
题目链接:https://leetcode.cn/problems/univalued-binary-tree/description/
我们先来看看题目描述以及相关示例:
这道题要求我们查看一颗二叉树里面所有节点存放的值是否相同,比较简单,相当于考察我们的链式二叉树中递归的学习,以及对遍历的理解,可以自己先尝试着做一做,然后再来看后面的解析和答案
首先我们来说解析,这个题我们还是需要使用递归的思想,就是“以大化小”,将大的问题转化为一个又一个的子问题,按照这种思路我们来重新解释一下这道题:
首先看根节点和左右子树根节点是否相同,如果相同就看左右子树是否同时为单值二叉树,我们就将这个大问题转化为了根节点和左右子树根节点的比较,以及左右是否为单值二叉树这样的小问题
或者说这样理解也可以,就是这道题需要我们遍历整颗二叉树,在我们遍历整颗二叉树时,每遍历一个节点就判断一下当前节点和它的左右孩子是否相等,当然,在这之前我们需要判断左右孩子是否存在
相当于就是根节点和它的左右孩子的值作比较,然后根节点的左右孩子也有自己的左右孩子,让它们的左右孩子继续和自己的左右孩子进行比较,这样就相当于在递归,跟我们的遍历很相似
但是最后我们发现这两个思路是高度重合的,甚至可以说就是一个思想说了两遍,但是不管怎样,我们对单值二叉树有了更深的了解,接下来来说说具体做法
首先我们需要判断根节点是否为空,如果为空就返回true,如果不为空的话,先判断左右孩子是否为空,跟不为空的孩子做比较,如果发现某个孩子的值和根节点不同,就返回false
如果和左右孩子比较后发现相同就去递归左右孩子,将整颗子树是否是单值二叉树问题转化为左子树和右子树是否同时为单值二叉树这样的递归思想,那么有了思路我们就来写代码,如下:
bool isUnivalTree(struct TreeNode* root)
{
//首先判断根节点是否为空,为空返回true
if(root == NULL)
{
return true;
}
//如果左孩子不为空,看看左孩子和根节点是否相同,不同就返回假
if(root->left && root->left->val != root->val)
{
return false;
}
//如果右孩子不为空,看看右孩子和根节点是否相同,不相同就返回假
if(root->right && root->right->val != root->val)
{
return false;
}
//递归左右子树
bool left = isUnivalTree(root->left);
bool right = isUnivalTree(root->right);
//只有左右子树都为单值二叉树才返回true
return left && right;
}
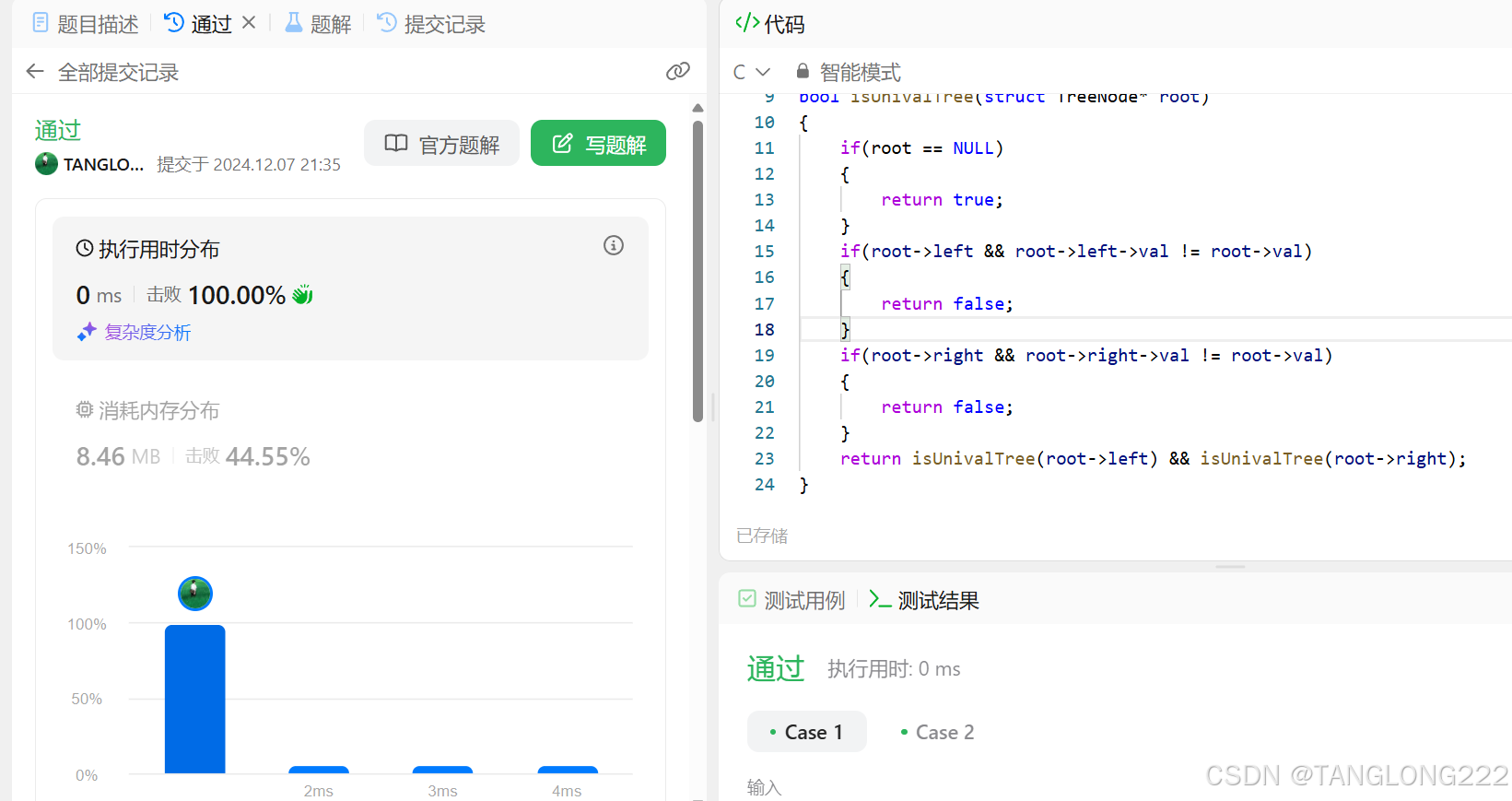
我们来看看代码提交结果:
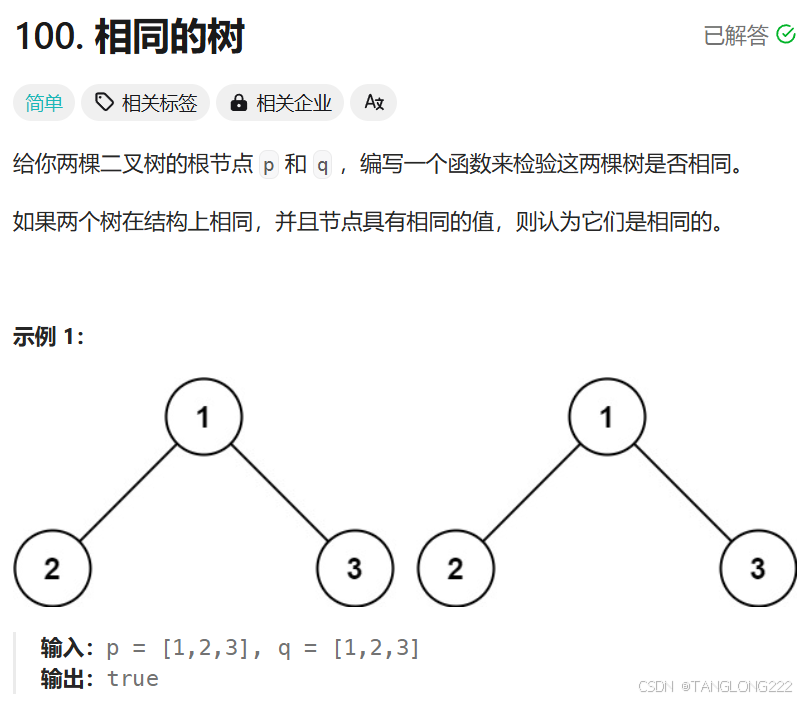
三、相同的树
题目链接:https://leetcode.cn/problems/same-tree/description/
我们来看看题目描述以及示例:
这道题要求的是给我们两颗二叉树的根节点,判断这两颗树是否相同,这道题也是和遍历的思想差不多,只是需要遍历时判断对应节点里面保存的值是否相同,可以先自己尝试写一写再看后面的解析和答案
首先我们来说解析,这个题我们还是需要使用递归的思想,就是“以大化小”,将大的问题转化为一个又一个的子问题,按照这种思路我们来重新解释一下这道题:
首先看两颗二叉树的根节点是否相同,如果相同的话,再看看左子树和右子树是否同时相同,于是判断两颗二叉树是否相同就分化成了,判断根节点是否相同,左右子树是否同时相同
那么具体怎么做呢?具体做法就是,先看看是否两颗二叉树都为空,如果都为空的话可以直接返回true了,随后我们要继续判断,因为虽然不是两颗二叉树都为空,但是有可能有一颗二叉树为空,一颗不为空,这时就要返回false了
随后我们保证两颗二叉树都不为空后,再去比较它们的根节点是否相同,不相同就直接返回false了,如果相同的话就同时递归两颗二叉树的左子树,看看它们的左子树是否相同
然后递归它们的右子树,看看它们的右子树是否相同,如果它们的左右子树都分别相同,并且前面证明了根相同,那么说明这两颗二叉树就相同了,自然就会返回false了
那么有了思路我们就来按照思路写出代码,如下:
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//如果同时为空就返回true
if(p == NULL && q == NULL)
{
return true;
}
//如果一个为空,一个不为空就返回false
if(p == NULL || q == NULL)
{
return false;
}
//判断根节点
if(p->val != q->val)
{
return false;
}
//递归左右子树
bool left = isSameTree(p->left, q->left);
bool right = isSameTree(p->right, q->right);
//要左子树和右子树同时返回true才能说明两颗二叉树相同
return left && right;
}
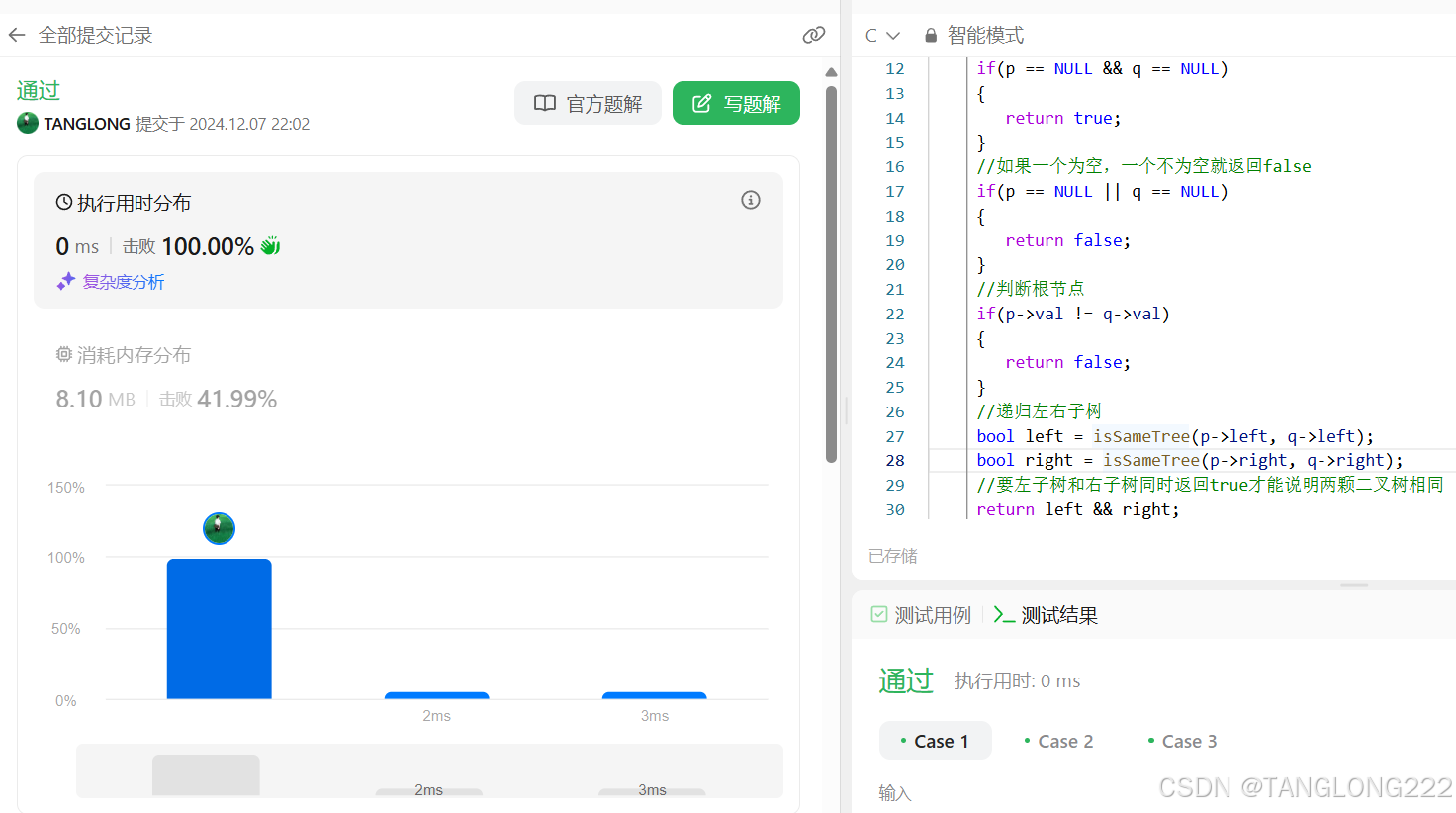
我们来提交一下代码,如图:
四、另一颗树的子树
题目链接:https://leetcode.cn/problems/subtree-of-another-tree/description/
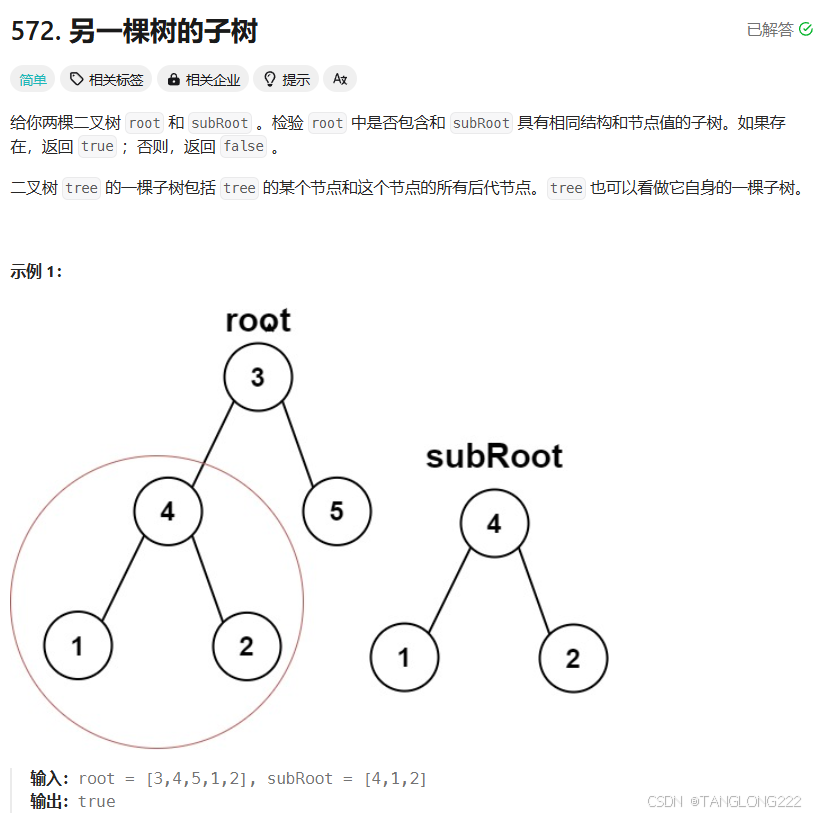
我们来看看题目描述和示例:
这道题是要求我们查看左边的二叉树里面的子树有没有和右边子树相同的,这道题相对于比前面的相同的树要稍微要难一点点,因为我们发现它们都是求树和树是否相同的问题,只是到这道题是查看左边的子树和右边的树是否相同,情况更为复杂
这道题和相同的树有很大的重合点,可以先自己思考一下,并不难,自己做一做之后再来看看这里的分析和答案,这样自己的代码能力才能得到锻炼
接下来我们开始分析,首先我们还是将题目用递归“以大化小”的思想重新解释一遍,这样方便我们理解,这个问题可以转化为,判断左边整颗二叉树和右边这颗二叉树是否是完全相同的
如果不同,我们再去看看左右子树里面有没有右边这颗二叉树,如果左右子树里面任意一颗树里面的子树和右边这颗二叉树相同,那么就说明整颗树里面确实有子树和右边的二叉树相同,否则就没有
当然,我们需要判断一些特殊情况,就是如果左右两颗二叉树同时为空,直接返回true,如果有一颗树为空,但是另一颗树不为空,那么就直接返回false,这就是这道题的大致思路了
那么我们最后到底该怎么做呢?首先就是,我们需要频繁的比较两颗二叉树是否相同,所以我们需要一个能判断两颗二叉树是否相同的函数,这不是正巧了,就是我们做过的上一题,直接把代码抄过来或者重新写一遍
然后我们就开始利用这个函数来判断左右子树是否直接相等了,相等就返回true,如果不相等的话我们就要递归查看左右子树中有没有和右边这颗二叉树的子树,然后根据返回值来进行判断
不需要左右子树中都有右边这颗二叉树的子树,只要有一颗子树有就可以了,所以它们之间是或的关系,这就是全部做法了,接下来我们就根据上面说的思路开始写代码了,如下:
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q == NULL)
{
return true;
}
if(p == NULL || q == NULL)
{
return false;
}
if(p->val != q->val)
{
return false;
}
bool left = isSameTree(p->left, q->left);
bool right = isSameTree(p->right, q->right);
return left && right;
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
//如果两颗树都为空就返回true
if(root == NULL && subRoot == NULL)
{
return true;
}
//如果其中一颗树为空,另一颗不为空就返回false
if(root == NULL || subRoot == NULL)
{
return false;
}
//如果当前这颗子树和右边的二叉树相同就直接返回true
if(isSameTree(root, subRoot))
{
return true;
}
//递归左右子树
bool left = isSubtree(root->left, subRoot);
bool right = isSubtree(root->right, subRoot);
//左右子树中有一颗子树里面的子树和右边的二叉树相同的话
//返回true,只有都没有找到才为false
return right || left;
}
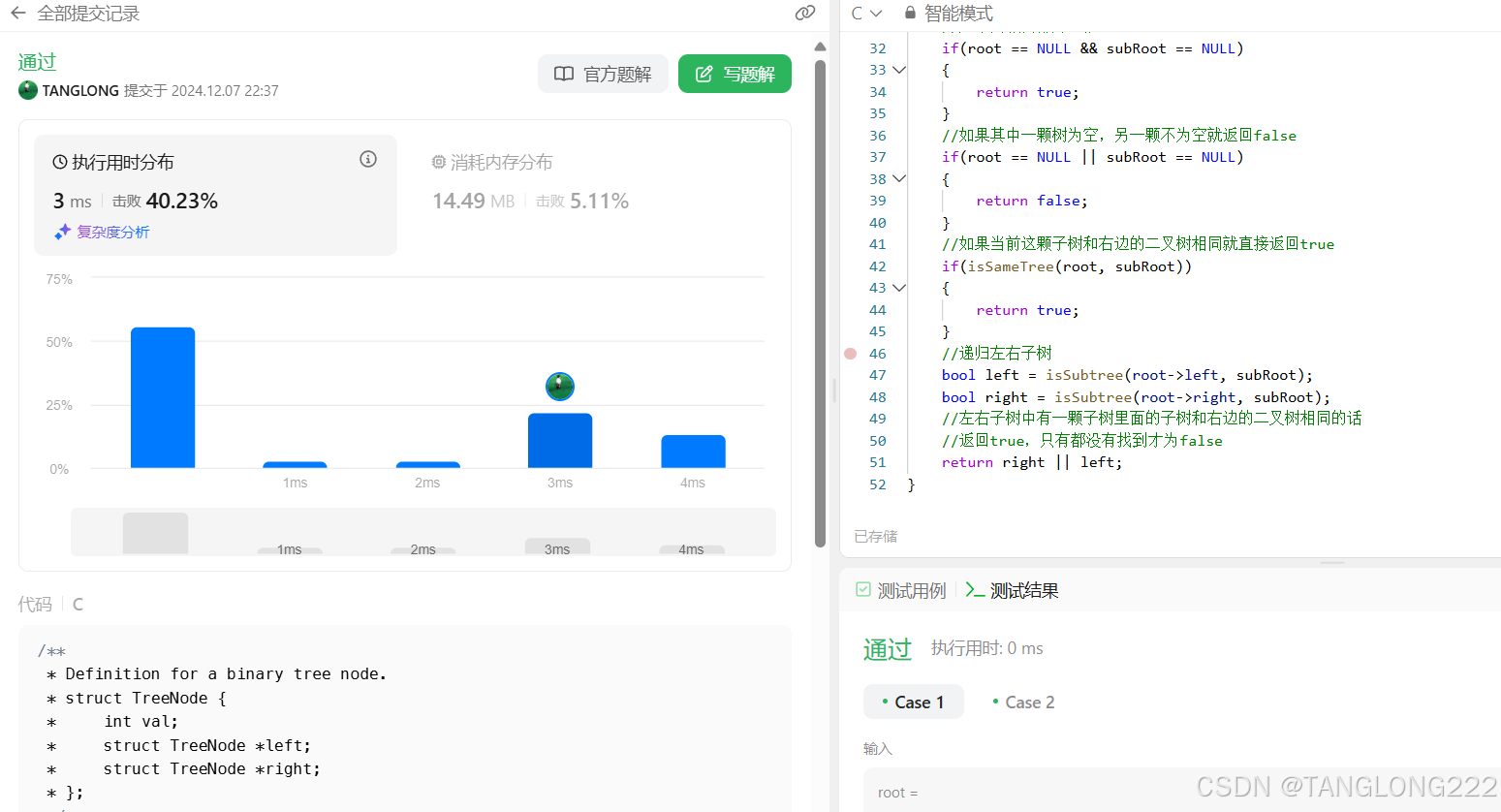
我们来看看代码提交结果:
五、对称二叉树
题目链接:https://leetcode.cn/problems/symmetric-tree/description/
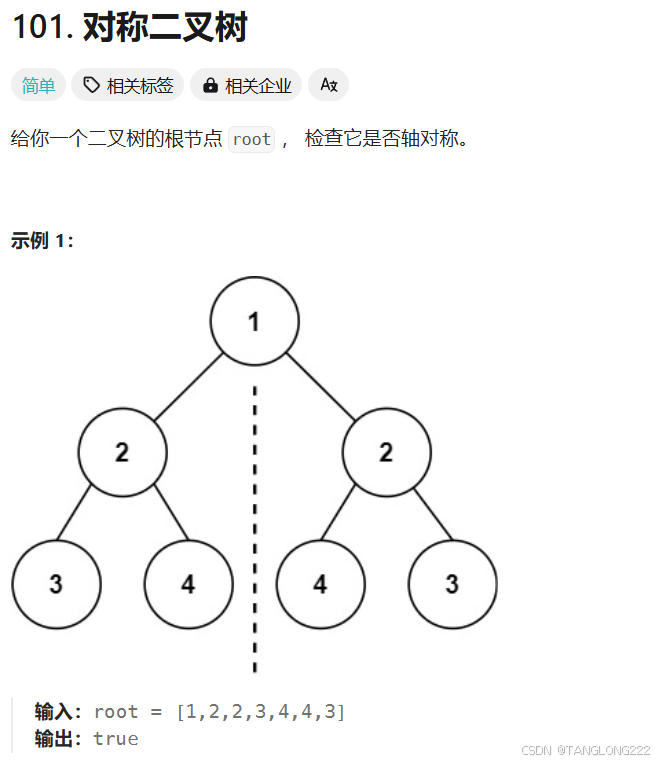
我们来看看题目描述和示例:
这道题要求我们查看一颗二叉树除了根节点以外是否对称,相比其它的题就要难一点了,但是其实跟我们前面做的相同的树这道题的思想还是很类似,只是思路略微复杂了一点,希望能够自己尝试思考并做一做,然后再来看分析以及答案
接下来我们开始分析,首先我们还是惯例,先用递归的思想“以大化小”来重新解释一下这道题,这道题我们可以不管根节点,而是只需要保证根节点左右孩子相同的情况下,左右孩子这两颗子树的子树互相对称
可能还是有点绕,所以直接说我们很难说清,我们来直接聊一聊它的做法,可能会给我们带来更多的启示,首先我们先看看根节点是否为空,如果为空直接返回false
然后我们就需要递归左右子树,但是同时我们要注意一点,左右子树又是单独的树,需要独立递归,但是这个题给出的函数参数只有一个,我们无法做到同时递归左右两颗树,所以我们需要创建一个子函数帮我们来进行递归这项任务
子函数就是我们真正函数的一部分,只是情况特殊或者代码比较长,所以我们才需要隔离,这里就是因为我们要使用递归,而原函数做不到,所以我们才创建一个子函数帮我们完成,一般子函数名就是原函数名前加一条下划线,如下:
原函数名为:isSymmetric
子函数名为:_isSymmetric
如果不理解也没关系,只要知道这个函数帮我们来实现递归左右子树的就行了,那么我们这个子函数就需要两个参数,分别是我们要处理的左子树的根节点以及右子树的根节点,返回类型还是bool,如下:
bool _isSymmetric(struct TreeNode* p, struct TreeNode* q)
然后我们在这个子函数中对这两颗子树做判断,其实不知道你们发现没有,我们的问题其实已经发生了变化,从判断一颗二叉树是否对称,变成了看给出的两颗二叉树是否对称,这样的好处是可以使用递归,因为如果函数只有一个参数不方便我们后面的递归
接下来我们就开始设计子函数,首先我们判断传来的两颗子树的根节点是否都为空,如果都为空那么就直接返回true,如果其中一颗为空,另一颗不为空就直接返回false
然后继续判断,走到这里说明两个根节点都不为空,那么如果要求这两颗子树对称,它们的根节点必须相同,所以我们判断一下它们的根节点是否相同,不相同就返回false
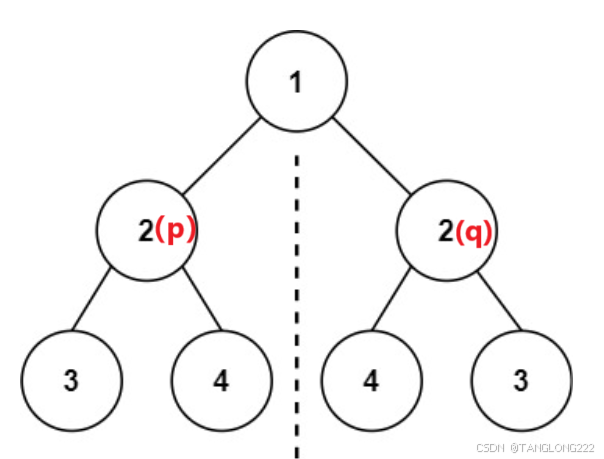
接下来就是这道题的重点,我们要保证这两颗二叉树对称,就需要它们的子树对称,所以我们接下来的递归就需要递归p的左子树和q的右子树,p的右子树和q的左子树,我们最好根据题目中示例图来理解,如下:
这里左边的p节点的左子树3和右边q节点的右子树3进行递归,它们都在外面,所以返回的结果用一个新的变量outside存起来,p节点的右子树4和q节点的右子树4进行递归,它们都在里面,所以返回的结果用新变量inside存起来
然后我们就判断outside和inside就可以了,必须保证outside和inside同时为真,也就是它们的递归的子树同时互相对称才行,才能说明整体的两颗二叉树对称,这就是关于对称二叉树这道题的所有分析了,有了思路我们就可以写代码了,如下:
//原函数的子函数,专门用来处理递归
bool _isSymmetric(struct TreeNode* p, struct TreeNode* q)
{
//如果同时为空,直接返回true
if(p == NULL && q == NULL)
{
return true;
}
//如果一个为空,一个不为空
//一定不对称,直接返回false
if(p == NULL || q == NULL)
{
return false;
}
//如果当前两个根的值不同,那么也不对称
//返回false
if(p->val != q->val)
{
return false;
}
//递归内外的子树
bool outside = _isSymmetric(p->left, q->right);
bool inside = _isSymmetric(p->right, q->left);
//内外都对称才说明这两颗树对称
return outside && inside;
}
bool isSymmetric(struct TreeNode* root)
{
//如果根为空,直接返回true
if(root == NULL)
{
return true;
}
//利用子函数递归左右子树
return _isSymmetric(root->left, root->right);
}
我们来看看代码提交结果:
那么今天二叉树链式结构的刷题训练就到这里结束了,下一篇我们总结一下所有我们学过的初阶数据结构,后面就可以开始学习排序算法了,敬请期待吧!
bye~