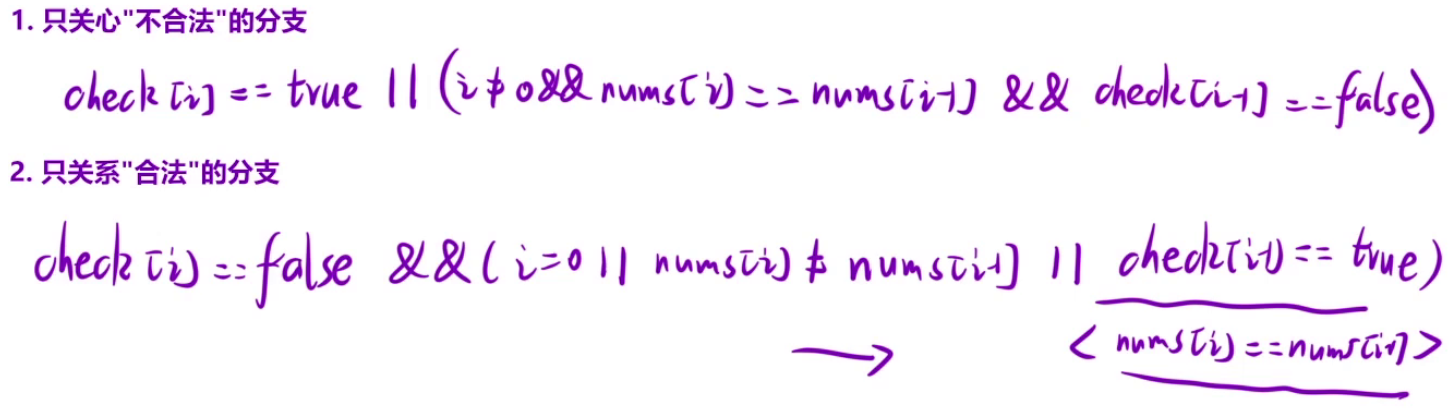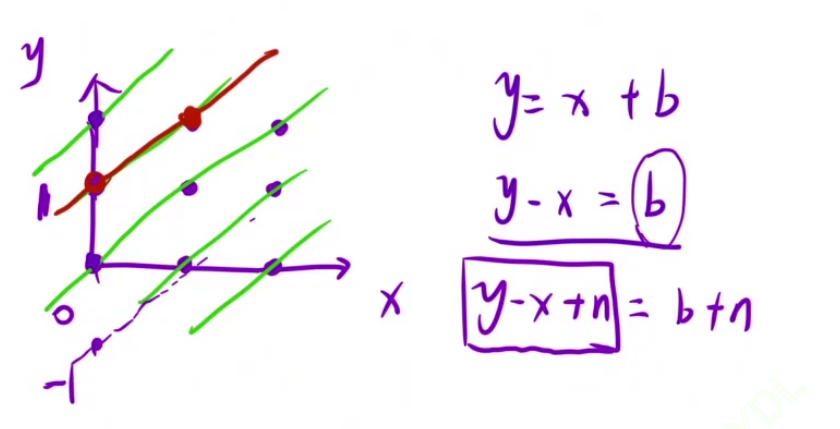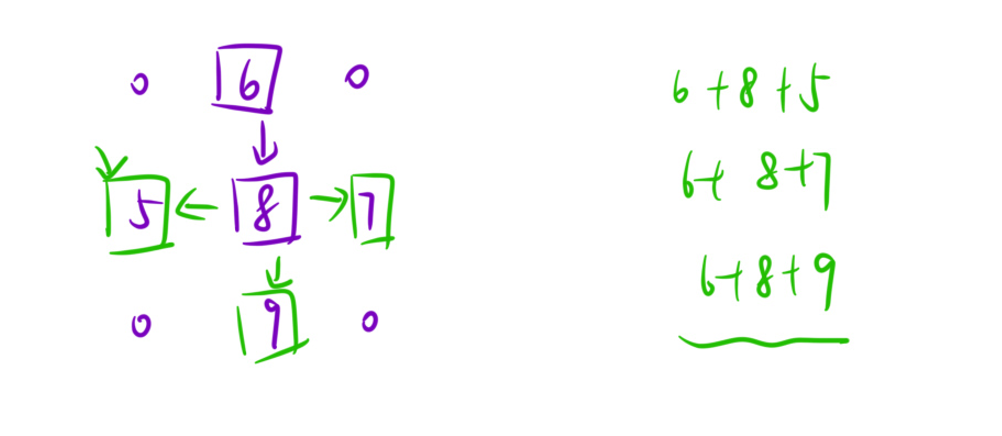专题介绍:
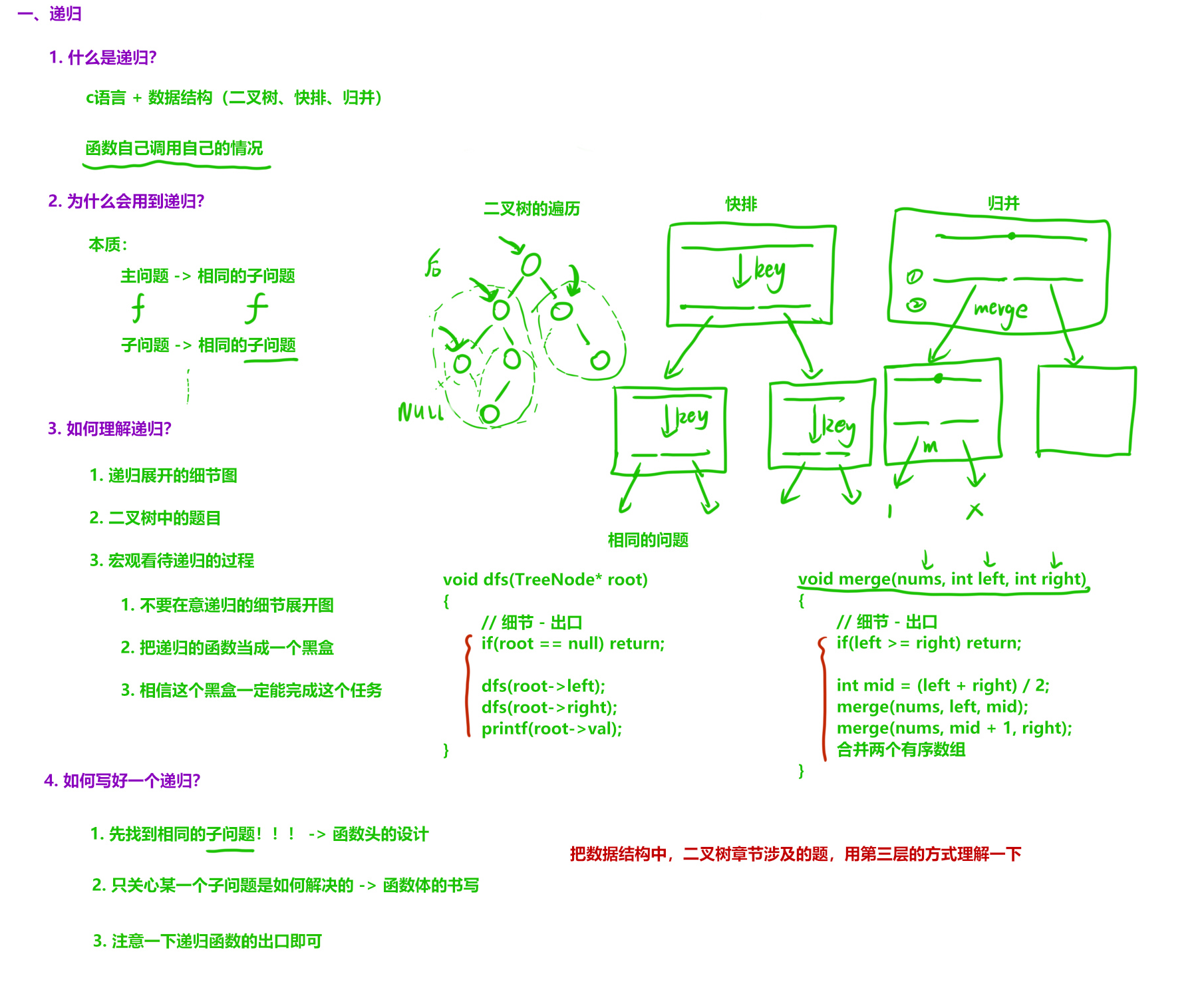
一、递归
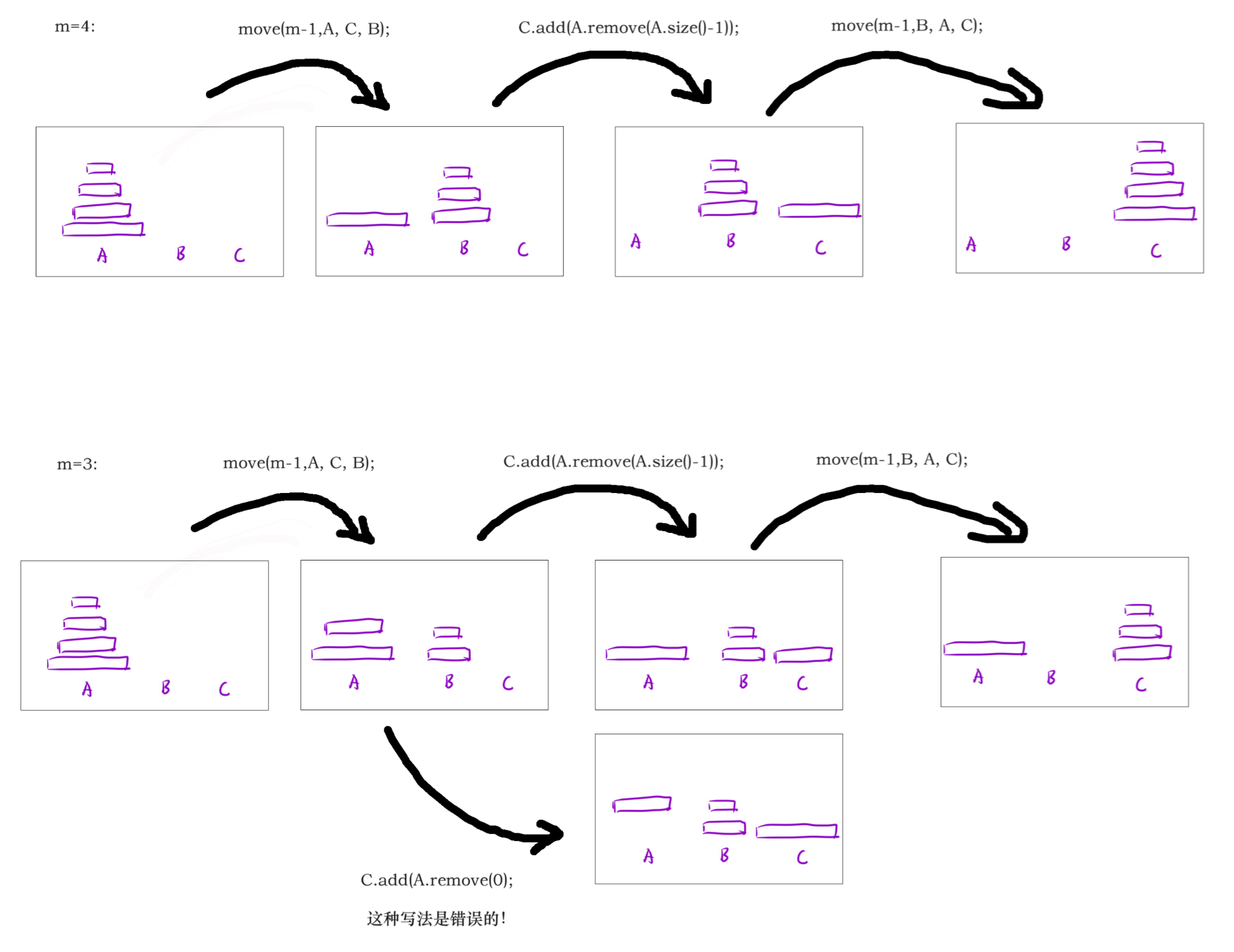
1、汉诺塔问题
class Solution {
public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
int n = A.size();
move(n,A,B,C);// 将A柱上的n个盘子通过借助B盘子全部挪到C柱子上
}
void move(int m,List<Integer> A, List<Integer> B, List<Integer> C) {
if (m == 1) {
C.add(A.remove(A.size()-1));
} else {
// 将A柱上的m-1个盘子通过借助C盘子全部挪到B柱子上,此时已经对A数列进行了元素删除
move(m-1,A, C, B);
// 挪动A柱子上的第1个盘子,也就是在没有对A进行修改时的第m个盘子。
// 这里容易写错成 C.add(A.remove(0));
C.add(A.remove(A.size()-1));
// 将B柱上的m-1个盘子通过借助A盘子全部挪到C柱子上,此时已经对A数列进行了元素删除
move(m-1,B, A, C);
}
}
}
// 蛮细节的一道题目
class Solution {
public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
int n=A.size();
move(n,A,B,C);
}
void move(int n, List<Integer> A, List<Integer> B, List<Integer> C) {
if (n == 1) {
C.add(A.remove(A.size() - 1));
} else {
// 这样写会有大盘子压小盘子的问题
B.add(A.remove(A.size() - 1));
move(n - 1, A, B, C);
C.add(B.remove(B.size() - 1));
}
}
}
// 思路错误,大盘子不能压小盘子
递归的思想,将问题转化为规模更小的子问题
// 相信move函数可以解决子问题
move(m-1,A, C, B);
C.add(A.remove(A.size()-1));
move(m-1,B, A, C);
// 通过自己调用自己解决原问题
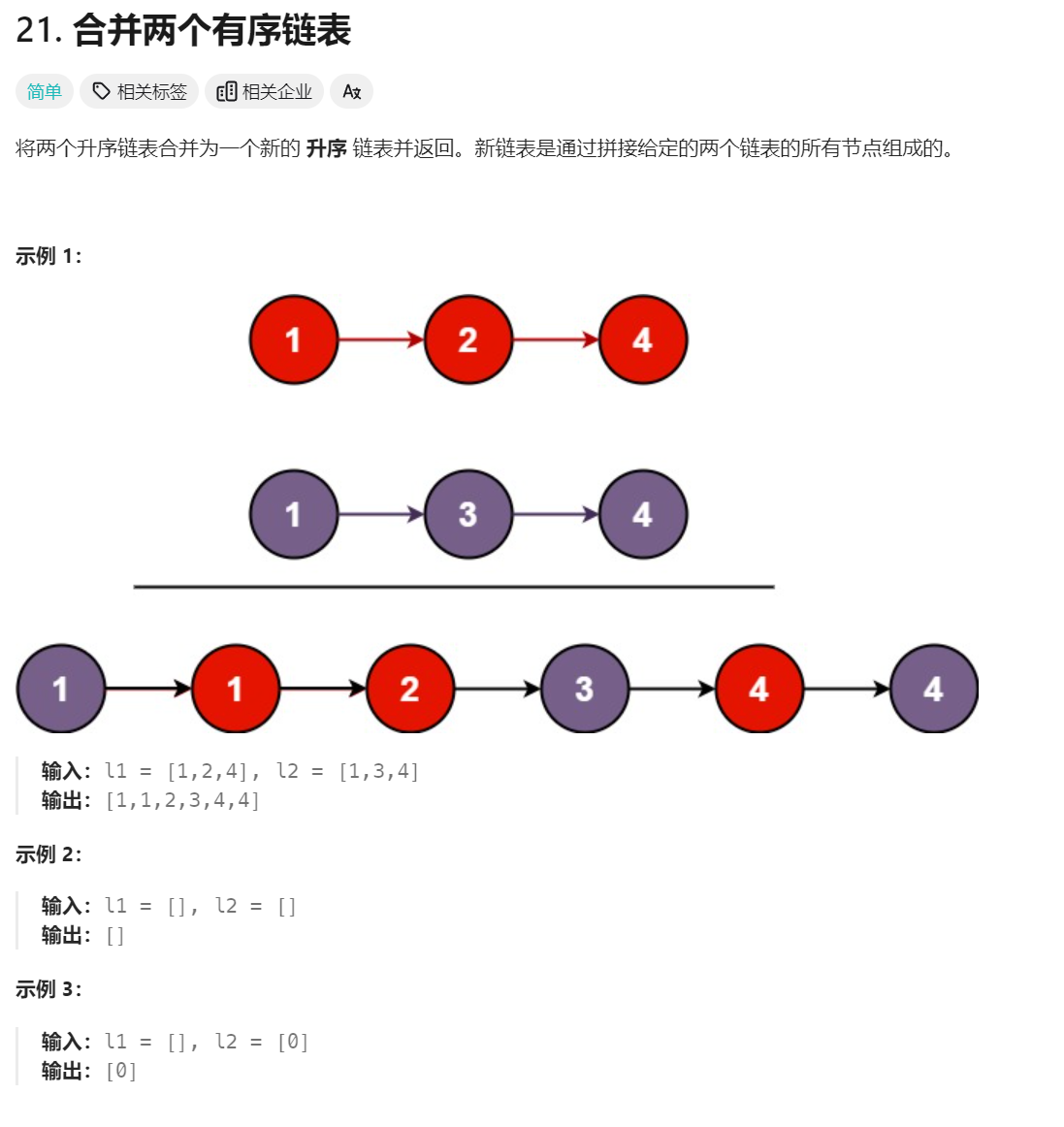
2、合并两个有序链表
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if(list1==null) return list2;
if(list2==null) return list1;
ListNode ret = new ListNode();
if(list1.val<list2.val){
ret.next = list1;
list1 = list1.next;
ListNode temp = mergeTwoLists(list1,list2);
ret.next.next = temp;
}else{
ret.next = list2;
list2 = list2.next;
ListNode temp = mergeTwoLists(list1,list2);
ret.next.next = temp;
}
return ret.next;
}
}
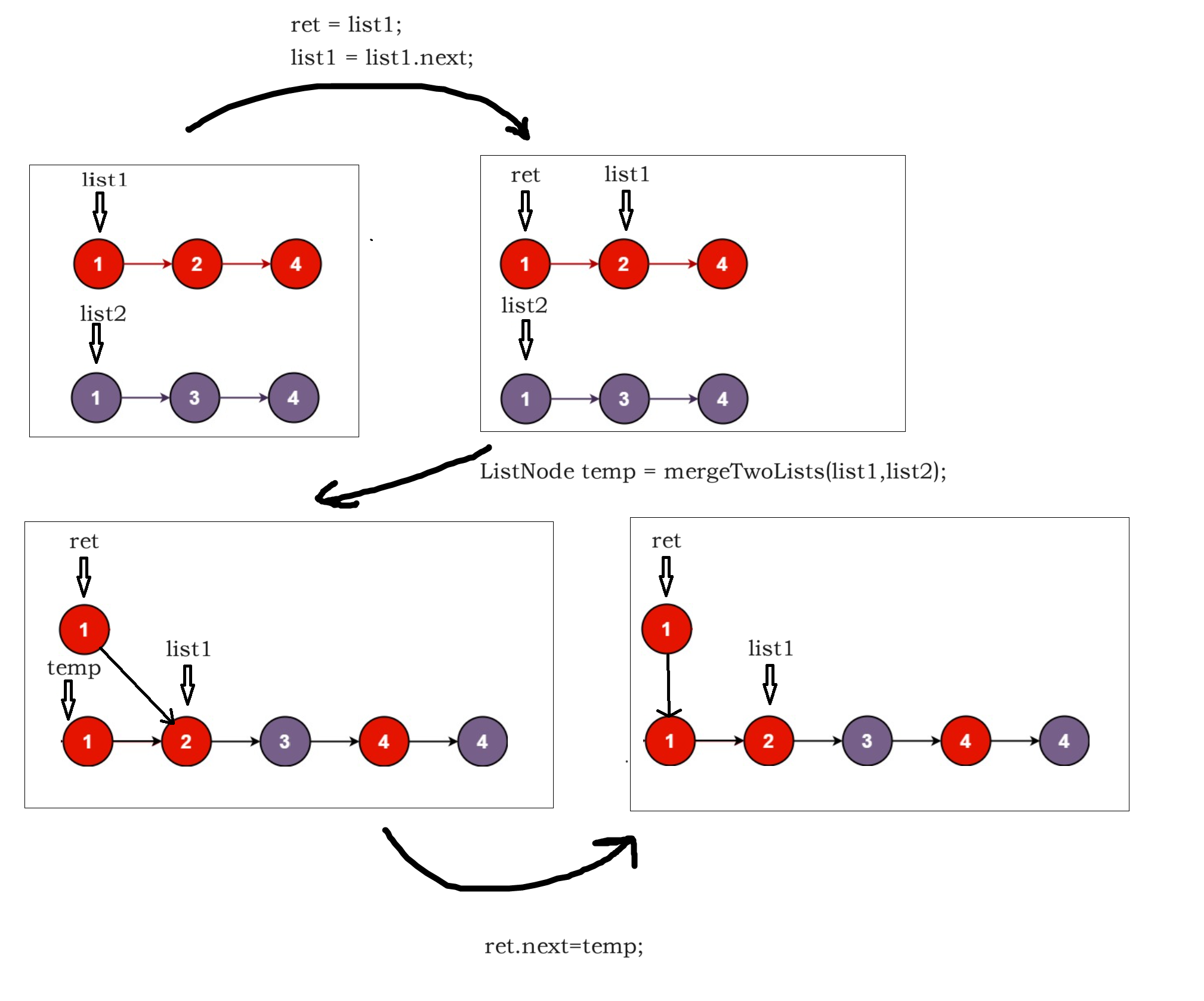
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if(list1==null) return list2;
if(list2==null) return list1;
ListNode ret = new ListNode();
if(list1.val<list2.val){
ret = list1;
list1 = list1.next;
ListNode temp = mergeTwoLists(list1,list2);
ret.next=temp; // 这一步很重要
}else{
ret = list2;
list2 = list2.next;
ListNode temp = mergeTwoLists(list1,list2);
ret.next=temp; // 这一步很重要
}
return ret;
}
}
尽量写一个递归函数就完成问题,汉诺塔问题递归函数需要四个参数,而题目只给了三个参数,所以需要创建一个单独的递归函数,然后使用驱动函数调用这个递归函数。
void main(int[] nums){
dfs(arr,0);
}
void dfs(int[] arr,int i){
// 顺序打印
cout << arr[i]<<' ';
dfs(arr,i+1);
// 逆序打印,只需要调换一下打印和调用的顺序即可。 前序遍历VS逆序遍历
// dfs(arr,i+1);
// cout << arr[i]<<' ';
}
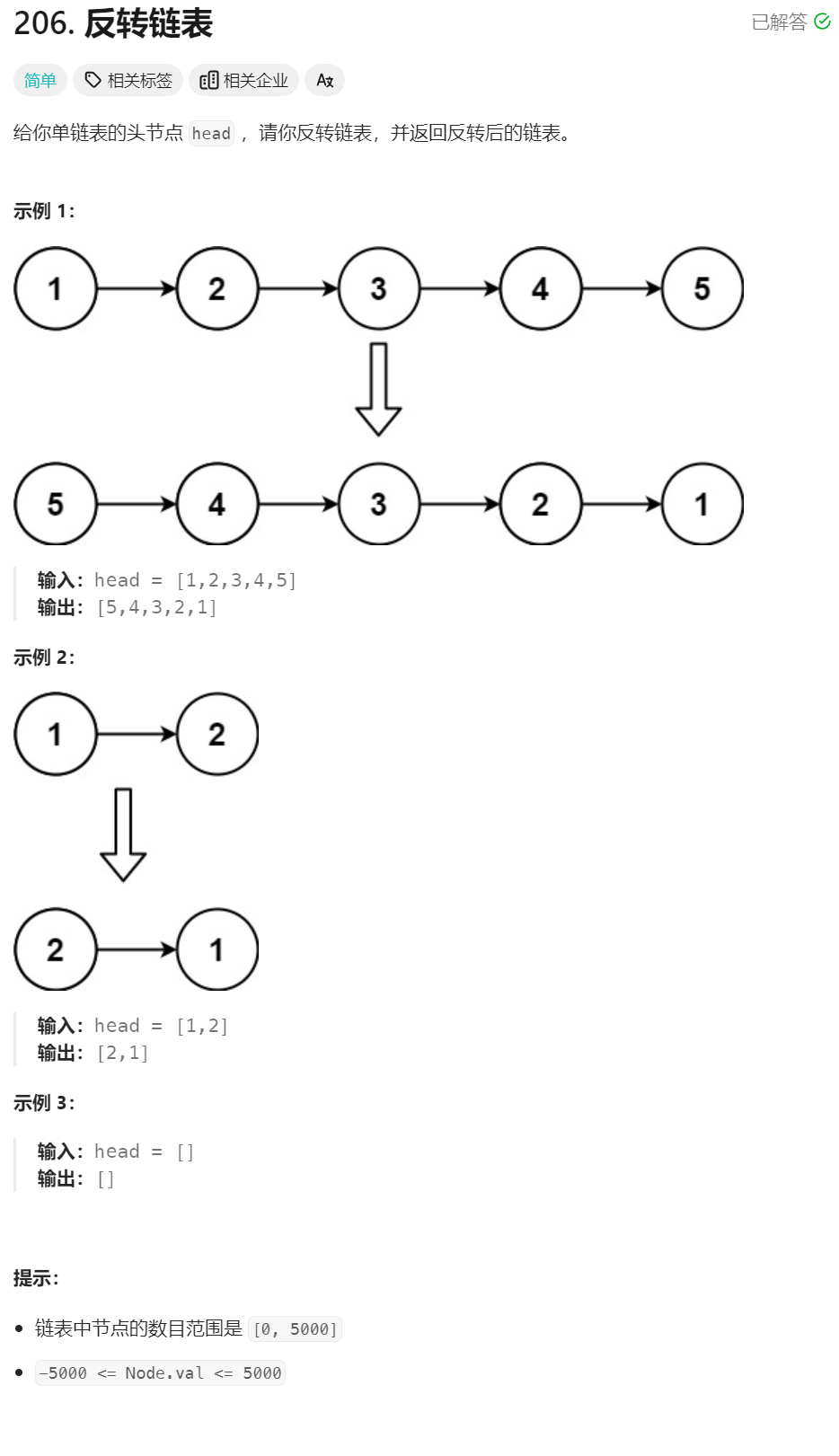
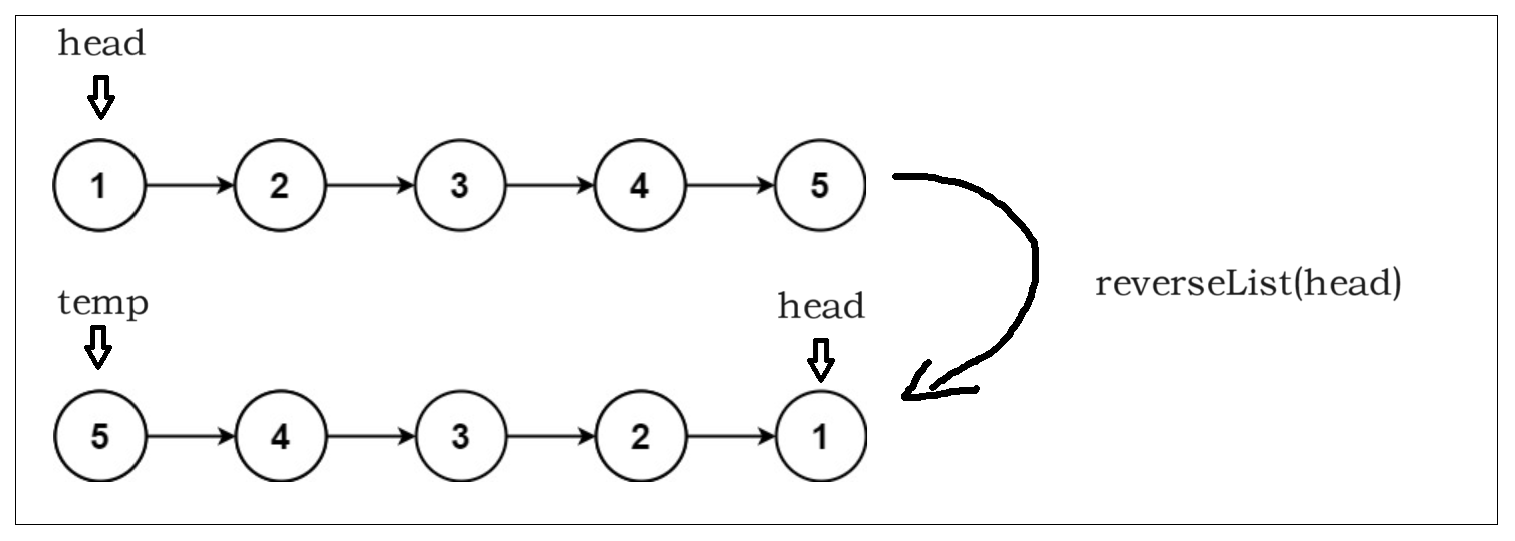
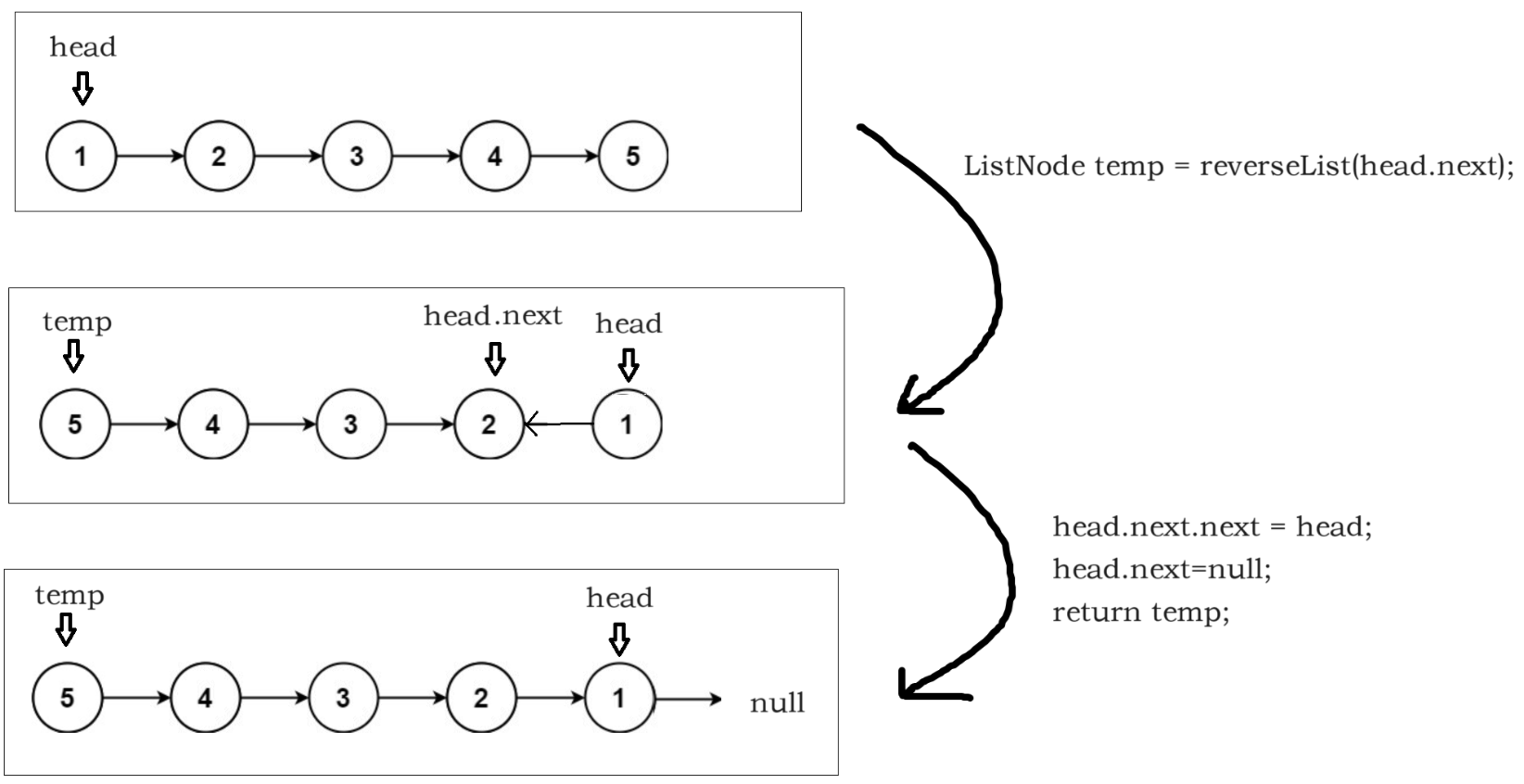
3、反转链表
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null)
return head;
ListNode temp = reverseList(head.next);
head.next.next = head;
head.next=null;
return temp;
}
}
递归函数:将以head为头结点的链表逆序,然会一个新的指针指向逆序链表的头结点,head依然指向原来的结点也就是逆序列表的为节点。
递归函数应该还可以这样去定义:将以head为头结点的链表针逆序,逆序后head指向逆序列表的头结点,该递归函数无需返回值,有也行。应该可以,挖坑。
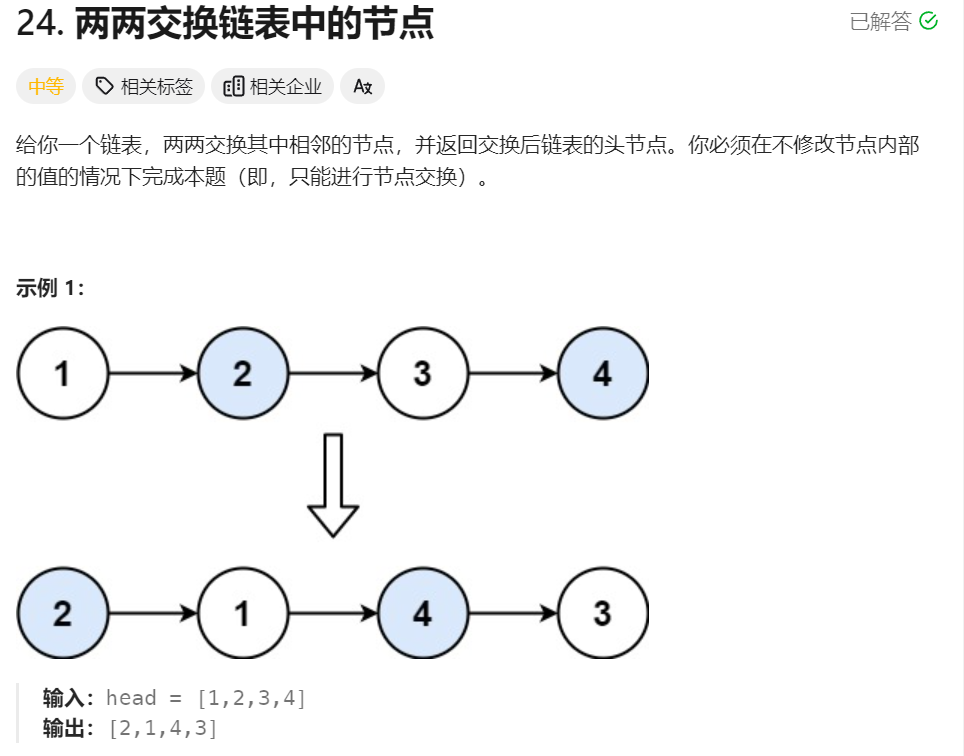
4、两两交换链表中的结点
class Solution {
public ListNode swapPairs(ListNode head) {
if(head==null||head.next==null) return head;
ListNode next = head.next;
head.next = head.next.next;
next.next = head;
ListNode temp = swapPairs(head.next);
head.next = temp;
return next;
}
}
将递归函数看成一个黑盒子,相信他可以解决子问题。
5、Pow(x, n)
class Solution {
public double myPow(double x, int n) {
if(n>=0) return fun(x,n);
else return 1/fun(x,-n);
}
public double fun(double x,int n){
if(n==0) return 1;
double a = fun(x,n/2); // 两次用到这个值,提前计算出来减少递归次数
if(n%2==0){
return a*a;
}else{
return a*a*x;
}
}
}
// 可以通过
class Solution {
public double myPow(double x, int n) {
if(n>=0) return fun(x,n);
else return 1/fun(x,-n);
}
public double fun(double x,int n){
if(n==0) return 1;
double a = fun(x,n/2); // 两次用到这个值,提前计算出来减少递归次数
if(n%2==1){
return a*a*x;
}else{
return a*a;
}
}
}
// 不能通过
// 当n=-n=-2147483648,-n也等于n=-2147483648
// 在不断调用fun的过程中n始终小于等于0,n%2不可能等于1
// fun(x,-2147483648)最终结果等于1,导致结果给错误
// fun(double x,int x);必须保证n>=0;对于这种特例要么特判,要么就是使用long整形进行传参
class Solution {
public double myPow(double x, int n) {
long m = (long)n;
if(m>=0) return fun(x,m);
else return 1/fun(x,-m);
}
public double fun(double x,long n){
if(n==0) return 1;
double a = fun(x,n/2); // 两次用到这个值,提前计算出来减少递归次数
if(n%2==1){
return a*a*x;
}else{
return a*a;
}
}
}
二、二叉树中的深搜
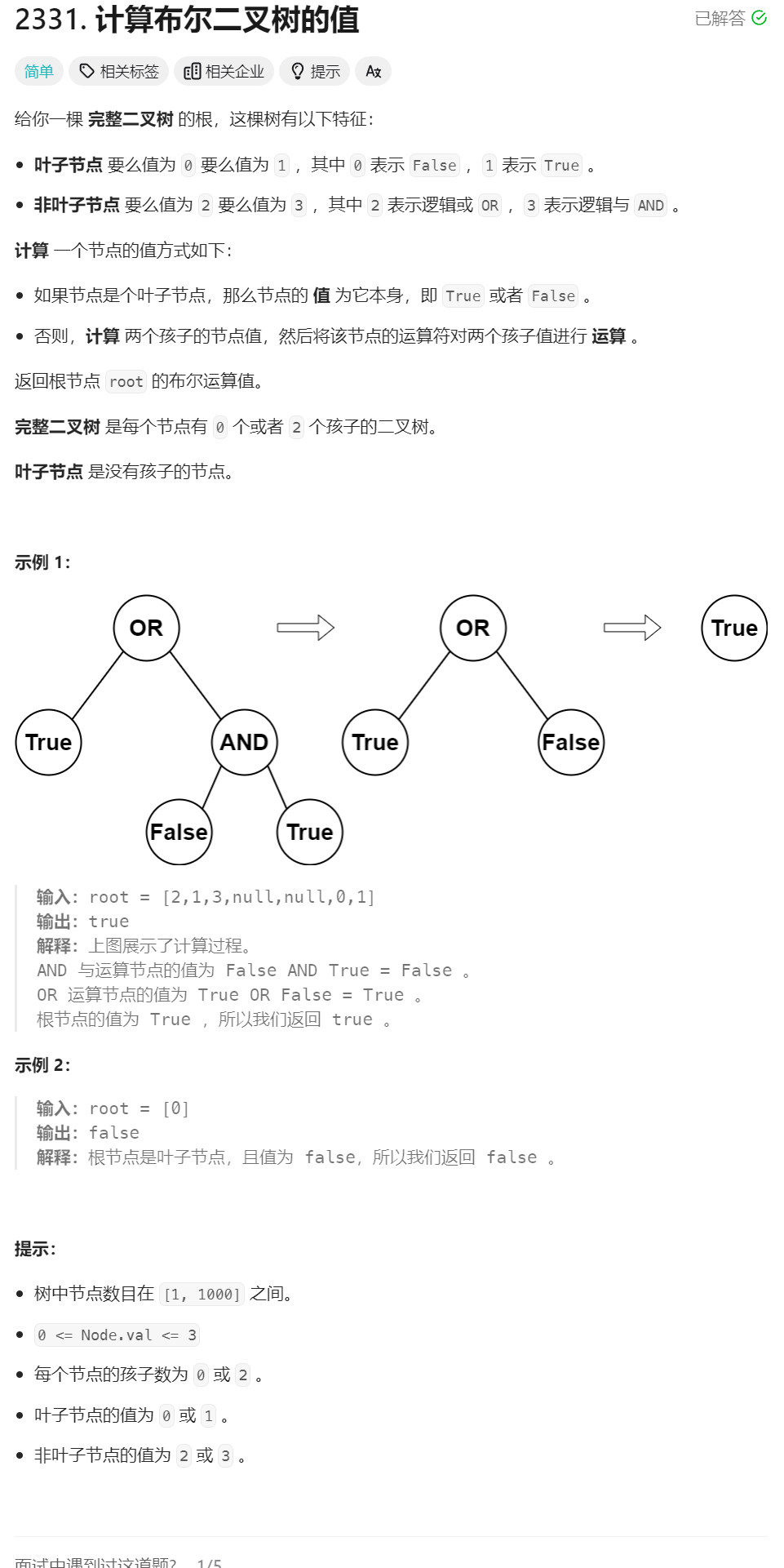
6、计算布尔二叉树的值
class Solution {
public boolean evaluateTree(TreeNode root) {
if(root.val==0) return false;
if(root.val==1) return true;
boolean left = evaluateTree(root.left);
boolean right = evaluateTree(root.right);// 我是瞎子,我把这里写成了root.right
if(root.val==2) return left || right;
return left && right;
}
}
// 整个代码就是后续遍历
原问题:根据题意计算root的值
子问题:根据题意计算某个分支节点的值
最小子问题:叶子节点
因为问题中只牵扯了root,所以题目给的函数就是递归函数
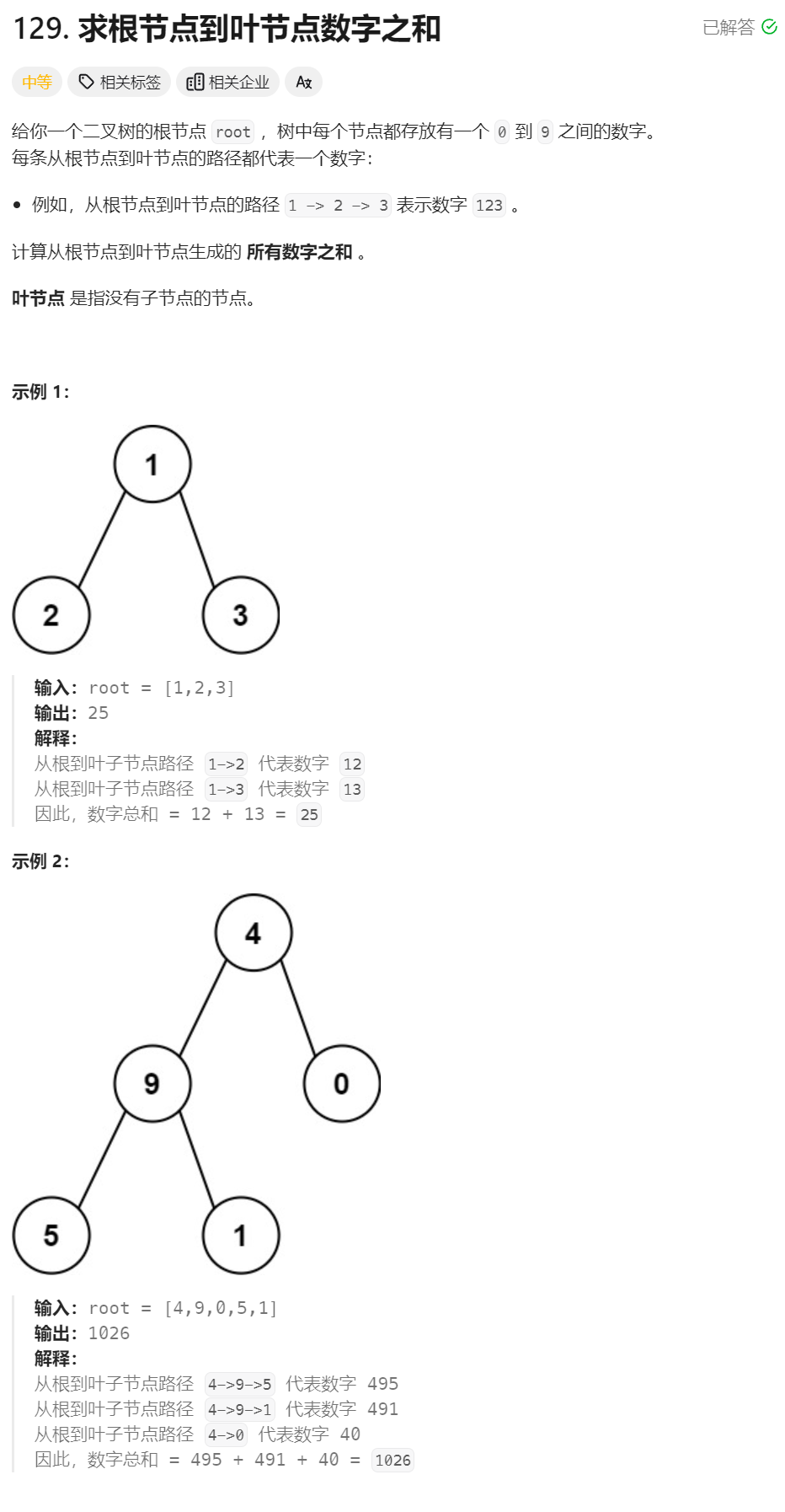
7、求根节点到叶子节点数字之和 ★★★★
class Solution {
public int sumNumbers(TreeNode root) {
return sum(0,root);
}
public int sum(int val,TreeNode root){
// 到达叶子节点就返回这条路径的数值
if(root!=null&&root.left==null&&root.right==null) return val*10+root.val;
int sum = 0;
// 有叶子节点就继续递归
if(root.left!=null) sum += sum(val*10+root.val,root.left);
if(root.right!=null) sum += sum(val*10+root.val,root.right);
return sum;
}
}
遍历到叶子节点的时候路径的数组已经被算出来了,然后返回相加即可。
子问题:有一个正数val和一个二叉树root,求从根节点到叶子节点构成的所有数字之和
原问题:val=0,二叉树为root。
子问题:val为根节点到分支节点构成的数字,分支节点为根节点的二叉树
问题中牵扯两个变量,递归函数有两个参数,因此需要自定义一个递归函数,使用题目给定的函数作为驱动函数。
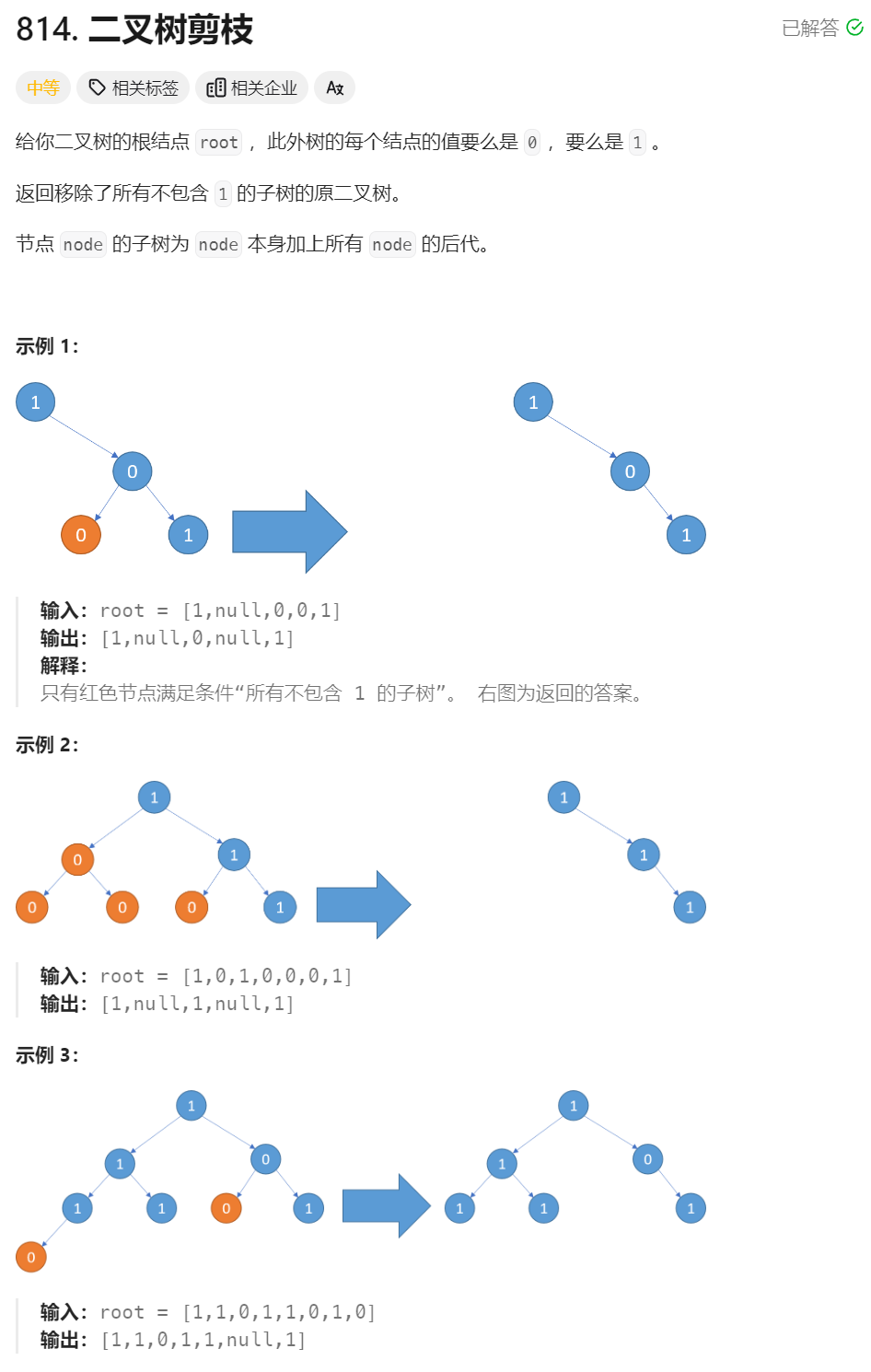
8、二叉树减枝头 ★★★★(函数函数传参)
class Solution {
public TreeNode pruneTree(TreeNode root) {
// 原问题:对root进行剪枝
// 子问题:对某个分支节点为根节点的二叉树进行剪枝
// 最小子问题(递归出口):叶子节点
// 0、递归出口,val为0的叶子节点
if (root == null)
return null;
// 1、修剪左右子树
TreeNode left = pruneTree(root.left);
TreeNode right = pruneTree(root.right);
// 2、修剪之后重新判断当前结点是否需要修剪
if (left == null && right == null && root.val == 0)
// 这一层的root是上一层的left或者right,修改root难道对上一层没有修改吗?
root = null;
// 3、返回值
return root;// 这个root只是临时变量吗???
}
}
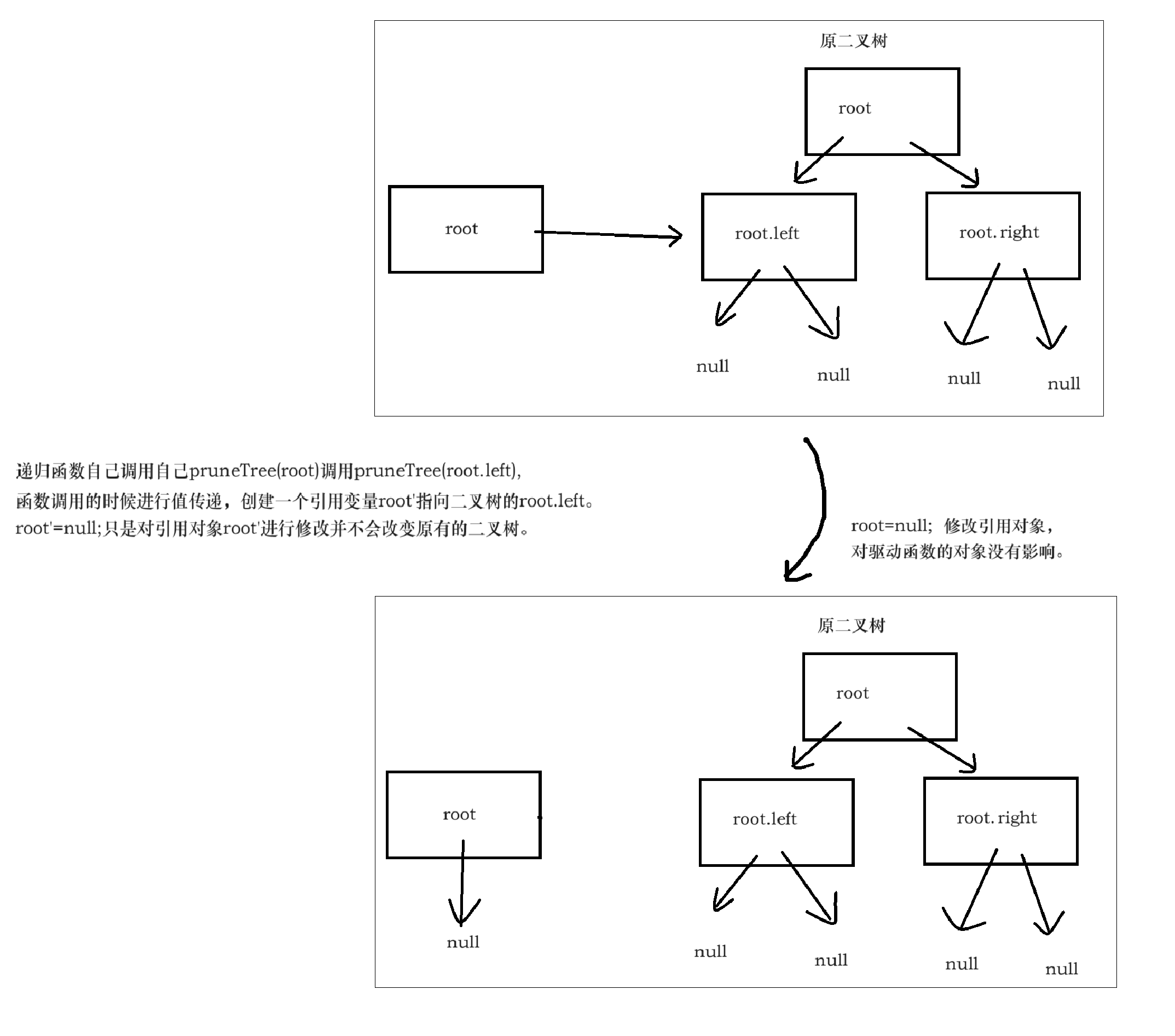
// 调试代码会发现,pruneTree并未对root做任何修改,说我只是修改了修改了临时变量
// 什么时候剪枝?
class Solution {
public TreeNode pruneTree(TreeNode root) {
// 原问题:对root进行剪枝
// 子问题:对某个分支节点为根节点的二叉树进行剪枝
// 最小子问题(递归出口):叶子节点
// 0、递归出口,val为0的叶子节点
if (root == null)
return null;
// 1、修剪左右子树
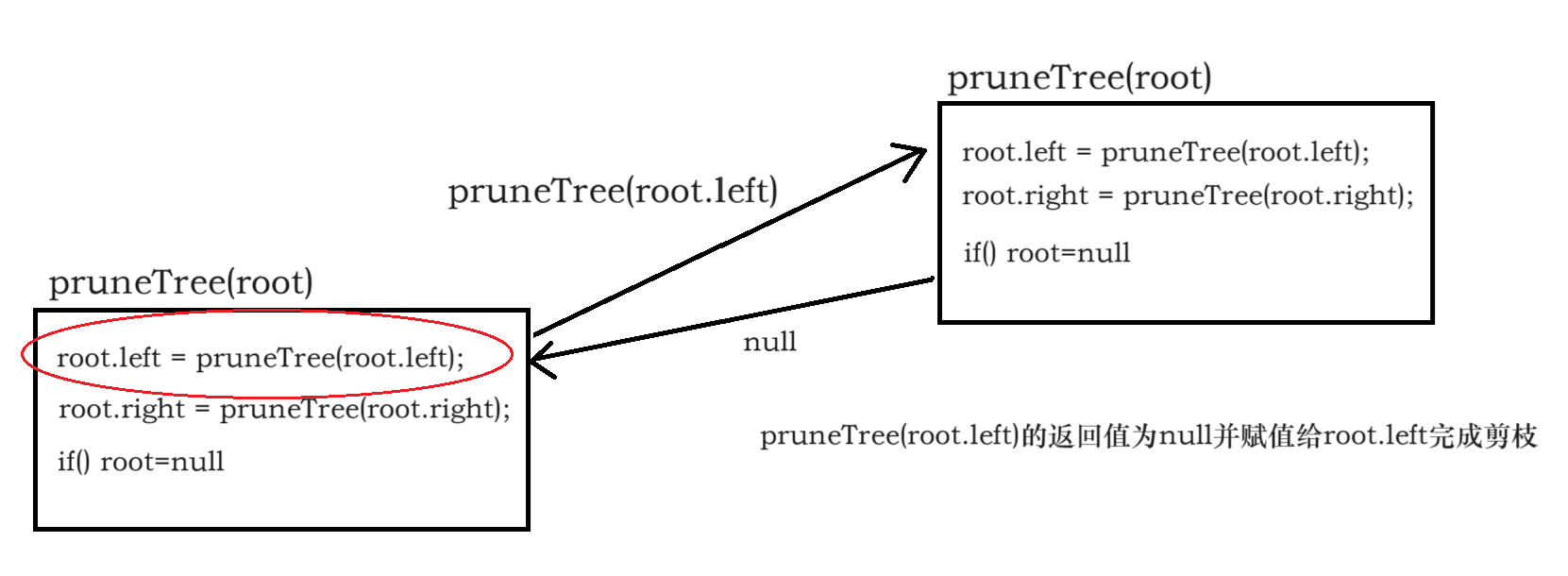
root.left = pruneTree(root.left);// 此处发生剪枝
root.right = pruneTree(root.right);// 此处发生剪枝
// 2、修剪之后重新判断当前结点是否需要修剪
if (root.left == null && root.right == null && root.val == 0)
root = null;
// 3、返回值
return root;
}
}
在Java中,所有函数参数传递都是“按值传递”的。但这里需要注意的是,对于基本数据类型(如int、char等)和对象类型,"按值传递"的行为是不同的:
- 基本数据类型:
public static void modifyValue(int x) {
x = 10;
}
public static void main(String[] args) {
int a = 5;
modifyValue(a);
System.out.println(a); // 输出仍为5
}
- 对于基本数据类型(如int、char等),Java会复制变量的值并传递给函数。因此,函数内对参数的修改不会影响函数外的原始变量。
- 对象类型:
class MyObject {
int value;
}
public static void modifyObject(MyObject obj) {
obj.value = 10; // 修改对象的属性,影响到原始对象
}
public static void reassignObject(MyObject obj) {
obj = new MyObject(); // 修改对象引用,不影响原始对象
obj.value = 20;
}
public static void main(String[] args) {
MyObject obj = new MyObject();
obj.value = 5;
modifyObject(obj);
System.out.println(obj.value); // 输出10
reassignObject(obj);
System.out.println(obj.value); // 输出10,reassignObject中的修改无效
}
- 对于对象类型(如类的实例),Java会复制对象引用的值并传递给函数。函数内部对对象属性的修改会影响到原始对象,因为它们共享同一个对象引用。
- 但如果在函数内部改变对象引用本身,这种改变不会影响到函数外的引用。
在**pruneTree**函数中的表现:
public static TreeNode pruneTree(TreeNode root) {
if (root == null)
return null;
TreeNode left = pruneTree(root.left);
TreeNode right = pruneTree(root.right);
if (left == null && right == null && root.val == 0)
root = null;
return root;
}
在这个函数中,root是一个对象引用。当函数被调用时,root的引用被复制传递给函数。因此,对root引用的修改(如将root设为null)并不会影响到原始的树结构,除非我们显式地将修改后的左子树和右子树重新赋值给root的左子树和右子树引用。
因此,修改后的版本如下:
public static TreeNode pruneTree(TreeNode root) {
if (root == null)
return null;
root.left = pruneTree(root.left); // 正确修改左子树
root.right = pruneTree(root.right); // 正确修改右子树
if (root.left == null && root.right == null && root.val == 0)
return null; // 返回null剪掉当前节点
return root;
}
这样做确保了递归调用的结果被正确赋值回root的左右子树指针,从而实现对树的有效剪枝。
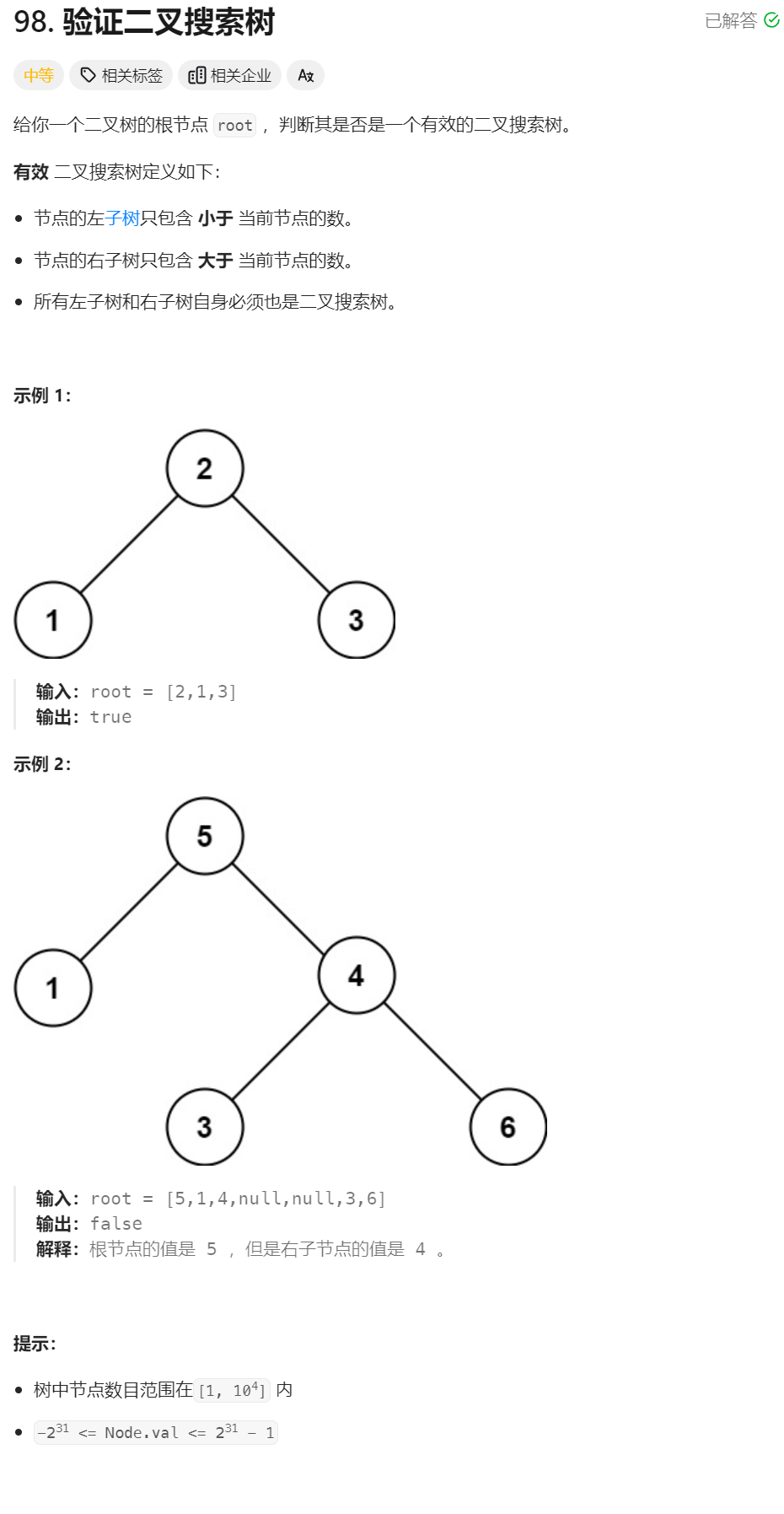
9、验证二叉搜索树
判断是否时二叉搜索树的方法:
- 根据定义来判断 (递归函数需要三个参数)
- 中序遍历二叉树的结果说递增的(使用一个全局变量标记前一个节点的值)
class Solution {
long prve = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
boolean left = isValidBST(root.left);
boolean cur = false;
if(root.val > prve) cur = true;
prve = root.val;
boolean right = isValidBST(root.right);
return left && cur && right;
}
}
class Solution {
long prve = Long.MIN_VALUE;
// 中序遍历
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
// 判断右节点
if(!isValidBST(root.left)) return false; //提前返回,剪枝操作
// 判断根节点
if(root.val<=prve) return false; // 提前返回,剪枝操作
// 更新prev
prve = (long)root.val;
// 判断左节点
return isValidBST(root.right);//剪枝操作
}
}
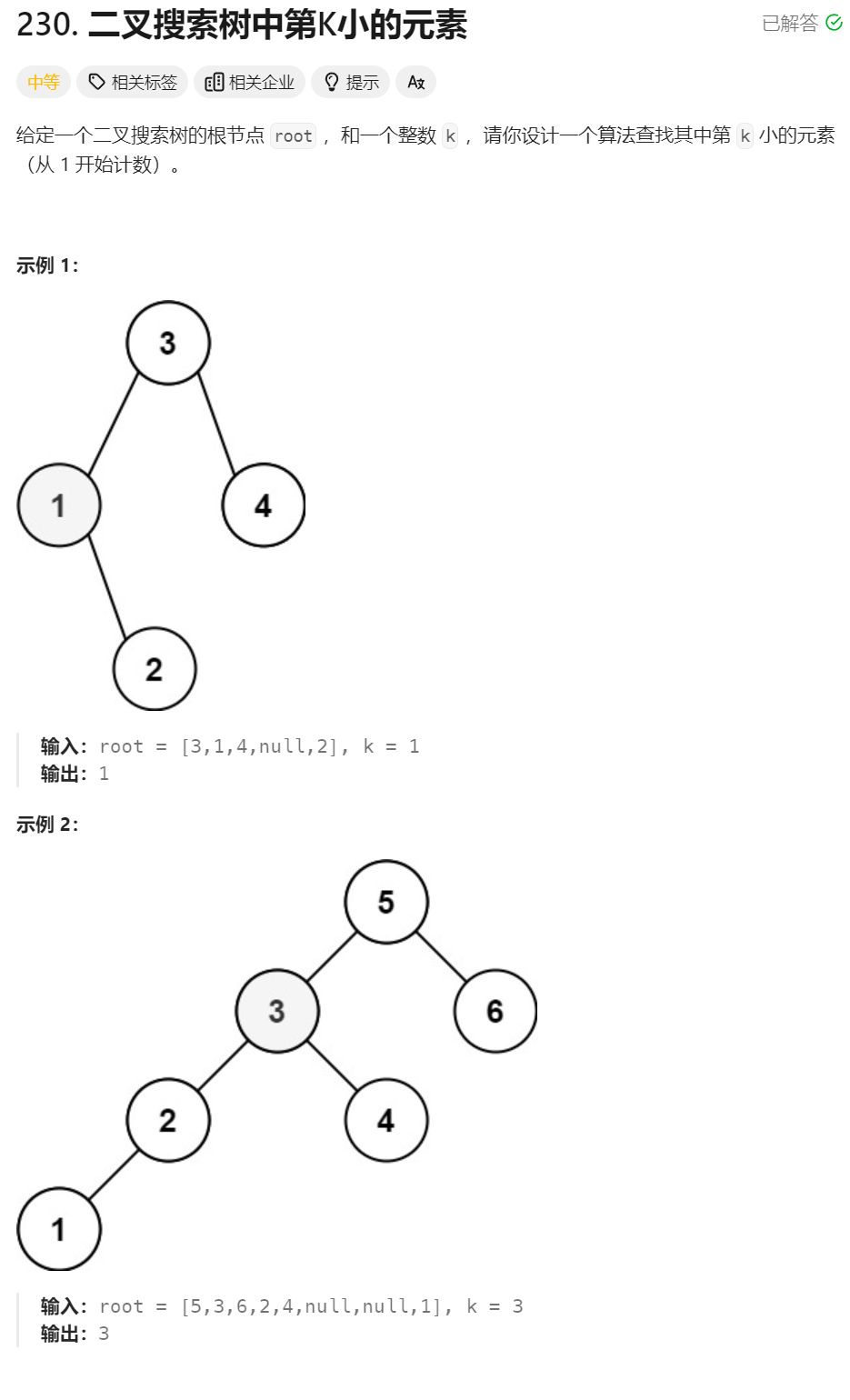
10、二叉搜索树中第k小的元素 ★★★★★(剪枝)
class Solution {
// k<=n 所以题目保证有结果
// 中序遍历二叉搜索的结果是递增的 => 寻找中序遍历的第k个数
int index = 0;
public int kthSmallest(TreeNode root, int k) {
if (root == null)
return -1;// 使用-1表示该节点不是第k小节点
int left = kthSmallest(root.left, k);
if (left != -1)
return left;
index++;
if (index == k)
return root.val;
return kthSmallest(root.right, k);
}
}
// 仔细观察可以发现,递归函数并不需要参数k
class Solution {
int count;
int ret;
public int kthSmallest(TreeNode root, int k) {
count = k;
dfs(root);
return ret;
}
// 返回值可能存在与右子树、根节点以及左子树,所以三个地方都可以进行剪枝操作
// 当已经找到答案的时候,后续的遍历都可以之间返回了。
void dfs(TreeNode root) {
if (root == null || count == 0) //剪枝一
return;
dfs(root.left);
if(count==0) return; //剪枝二
count--;
if (count == 0)
ret = root.val;
if (count == 0) // 剪枝三
return;
dfs(root.right);
}
}
class Solution {
int count;
public int kthSmallest(TreeNode root, int k) {
// 如果让count从0加到k,那么递归函数就需要k这个参数
// 如果初始化count=k,让count减到0,递归函数一个就不需要k这个参数了
count = k;
return dfs(root);
}
int dfs(TreeNode root) {
// count=0的作用:count是个全局变量,当count减到0的时候已经找到返回值了,后续的递归调用就不用再进行了,如果再进行count就会变成负数。
if (root == null || count == 0) // 剪枝一
return -1;
int left = dfs(root.left);
if(left!=-1) return left; // 剪枝二
count--;
if (count == 0) // 剪枝三
return root.val;
return dfs(root.right);
}
}
剪枝操作是机器学习和数据挖掘中的一种经常使用的技术,它的目的是减少模型的复杂性,防止过拟合,提高模型的泛化能力。剪枝的主要原理如下:
- 识别模型中相对重要性较低的参数或特征。这些参数或特征对模型的预测性能贡献较小,可以被删除而不会显著降低模型的性能。
- 通过移除这些不重要的参数或特征,可以减少模型的复杂度,从而降低过拟合的风险。过拟合通常会导致模型在训练集上表现良好,但在新的数据上表现较差。
- 剪枝后的模型通常更加简单和高效,在部署和使用时会更加快速和节省资源。
常见的剪枝方法包括:
- 基于阈值的剪枝:删除权重绝对值小于某个阈值的参数。
- 基于敏感度的剪枝:删除对模型性能影响较小的参数。
- 基于贪心算法的剪枝:递归地删除最不重要的参数。
- 基于正则化的剪枝:通过L1或L2正则化鼓励参数稀疏。
总之,剪枝是一种非常有效的技术,可以帮助我们构建更加简单和高效的模型,提高模型的泛化能力。在实际应用中,需要根据具体问题选择合适的剪枝方法。
剪枝操作的核心是在不显著降低模型性能的前提下,尽可能地减少模型的复杂度。这个核心可以概括为以下几个方面:
- 减少过拟合风险
- 过度复杂的模型容易发生过拟合,在训练集上表现良好但在新数据上泛化性能较差。
- 通过剪枝减少模型复杂度,可以有效降低过拟合的风险,提高模型的泛化能力。
- 提高模型效率
- 更简单的模型通常计算开销更小,在部署和应用时会更加快速和节省资源。
- 这对于一些对实时性和资源消耗有严格要求的场景非常重要,如移动端应用、嵌入式系统等。
- 增强模型可解释性
- 复杂的模型往往难以解释内部工作原理,而简单的模型通常更加可解释。
- 可解释性有利于模型的调试和修改,也有助于用户对模型的信任和接受。
- 避免不必要的复杂性
- 过于复杂的模型并非总是能提供更好的性能。相反,过度复杂可能带来不必要的开销。
- 通过剪枝找到适度复杂度的模型,既可以保证性能,又可以提高效率和可解释性。
综上所述,剪枝操作的核心就是在保持模型性能的前提下,尽可能地简化模型结构,从而降低过拟合风险、提高模型效率和可解释性。这是模型优化的重要手段之一。
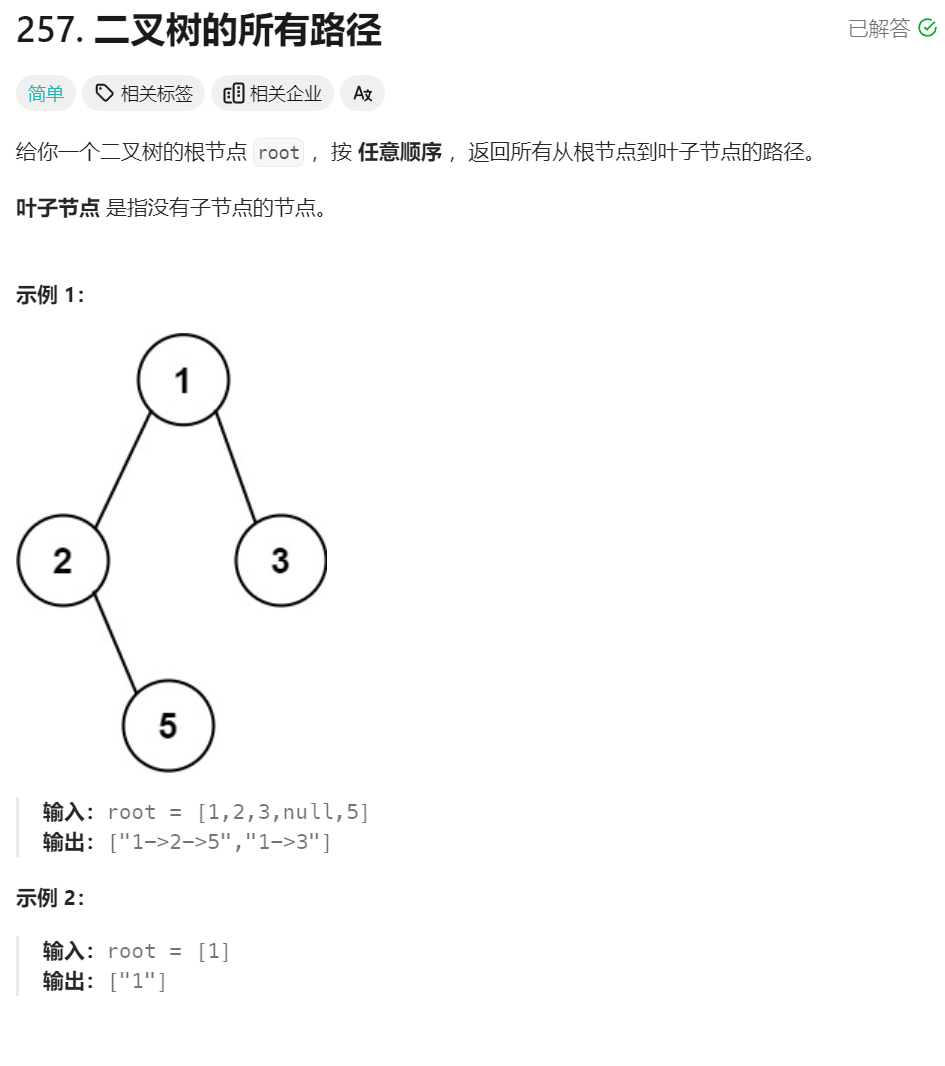
11、二叉树的所有路径 ★★★★(回溯、恢复现场)
class Solution {
// 全局变量
List<String> list = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
dfs(root,"");
return list;
}
public void dfs(TreeNode root,String path){
if(root == null) return;
// 叶子节点
if(root != null && root.left==null && root.right==null ){
path=path+"->"+root.val;
list.add(path.substring(2,path.length()));
return ;
}
path=path+"->"+root.val;
dfs(root.left,path);
dfs(root.right,path);
}
}
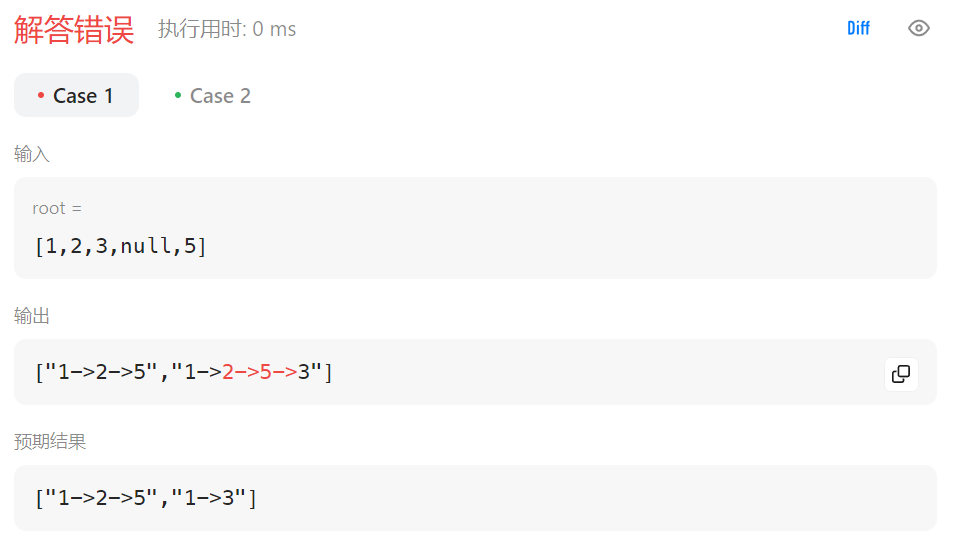
// path=path+"->"+root.val;该操作会new出来一个新的String对象,
// 对驱动函数中的path没有影响,因此手动实现“回复现场”
// path=path+"->"+root.val;这样操作会提高会消耗较长时间
class Solution {
// 全局变量
List<String> list = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
dfs(root,new StringBuffer(""));
return list;
}
public void dfs(TreeNode root,StringBuffer path){
if(root == null) return;
// 叶子节点
if(root != null && root.left==null && root.right==null ){
path.append("->");
path.append(root.val);
list.add(path.substring(2,path.length()));
return ;
}
path.append("->");
path.append(root.val);
dfs(root.left,path);
dfs(root.right,path);
}
}
// 被掉函数会修改StringBuffer对象的值,此时驱动函数的StringBuffer对象也会被修改,
// 如果不回溯就会影响递归调用
class Solution {
// 全局变量
List<String> list = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
dfs(root,new StringBuffer());
return list;
}
public void dfs(TreeNode root,StringBuffer _path){
// 回溯方法一:赋值一个临时变量
StringBuffer path = new StringBuffer(_path);
if(root == null) return;// 算不上剪枝,遍历到空节点了
path.append(root.val);
if(root.left==null && root.right==null ){
list.add(path.toString());
return ;
}
path.append("->");
dfs(root.left,path);
// 回溯方法二:删除"->"
dfs(root.right,path);
}
}
class Solution {
// 全局变量
List<String> list = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
dfs(root,new StringBuffer());
return list;
}
public void dfs(TreeNode root,StringBuffer _path){
StringBuffer path = new StringBuffer(_path);
path.append(root.val);
if(root.left==null && root.right==null ){
list.add(path.toString());
return ;
}
path.append("->");
if(root.left!=null) dfs(root.left,path);
if(root.right!=null) dfs(root.right,path);
}
}
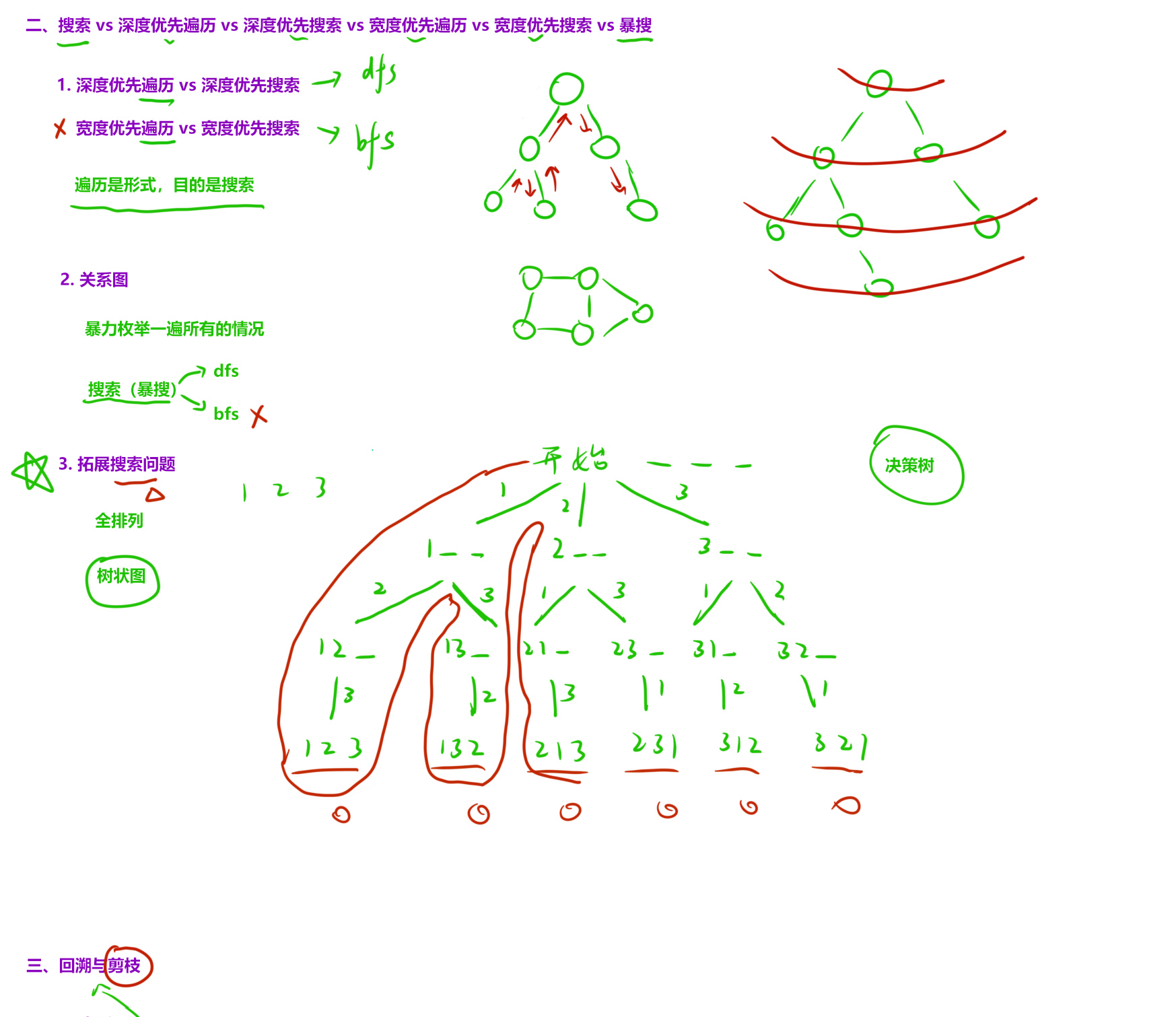
三、穷举vs暴搜vs深搜vs回溯vs剪枝
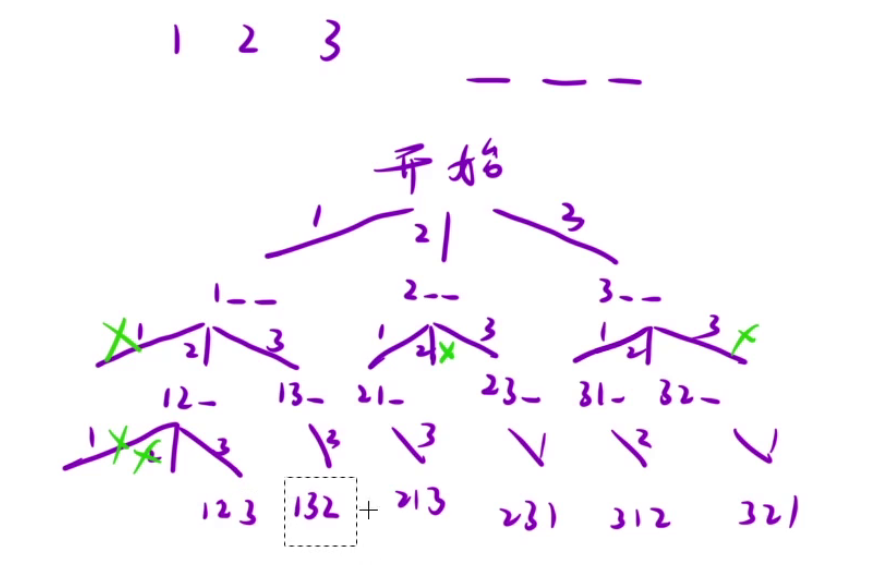
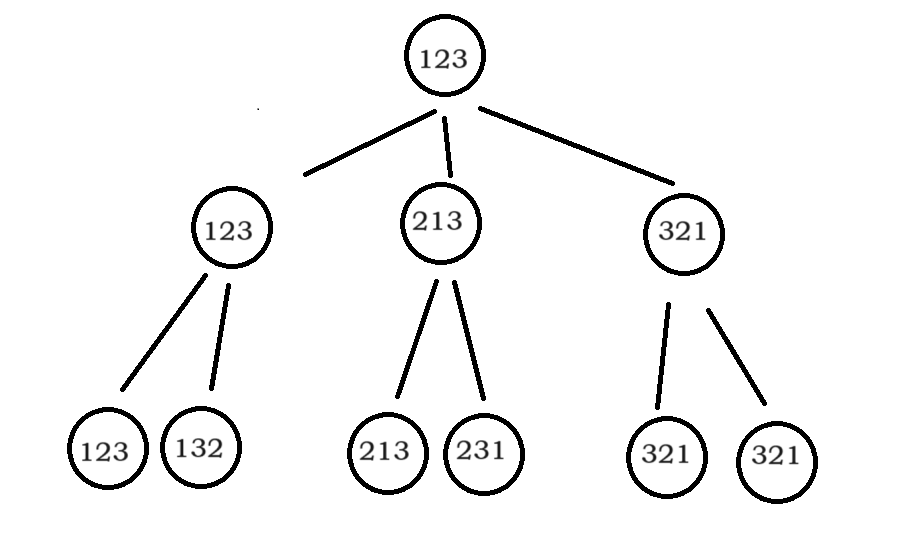
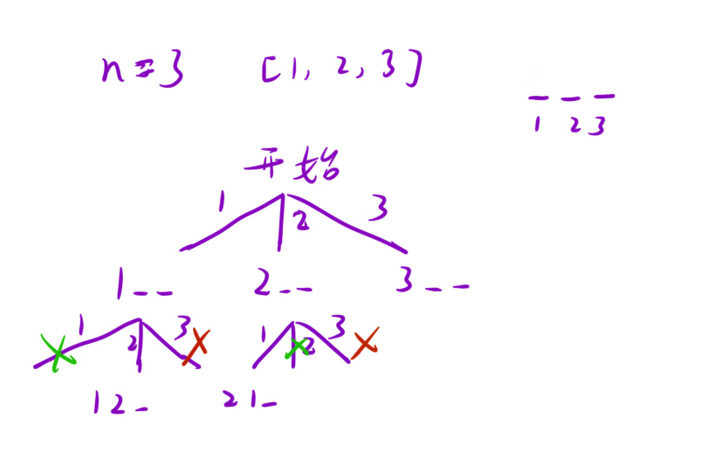
12、全排列 ★★★★(经典例题)
全排列的结果在叶子节点上
class Solution {
List<List<Integer>> ret = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
dfs(nums,0,nums.length);
return ret;
}
public void dfs(int[] nums,int index,int n){
if(index == n){
ret.add(Arrays.stream(nums).boxed().collect(Collectors.toList()));
}
for(int i=index;i<n;i++){
swap(nums,index,i);
dfs(nums,index+1,n);
swap(nums,index,i);
}
}
void swap(int[] nums,int i,int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
class Solution {
List<List<Integer>> ret = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
List<Integer> list = Arrays.stream(nums).boxed().collect(Collectors.toList());
dfs(list,0,nums.length);
return ret;
}
public void dfs(List<Integer> list,int index,int n){
if(index == n){
ret.add(new ArrayList<>(list));
}
for(int i=index;i<n;i++){
swap(list,index,i);
dfs(list,index+1,n);
swap(list,index,i);
}
}
void swap(List<Integer> list,int i,int j){
int a = list.get(i);
int b = list.get(j);
list.set(i,b);
list.set(j,a);
}
}
class Solution {
List<List<Integer>> ret;
List<Integer> path;
boolean[] cheak; // 用于标记第i个是否被使用过
public List<List<Integer>> permute(int[] nums) {
ret = new ArrayList<>();
path = new ArrayList<>();
cheak = new boolean[nums.length];
dfs(nums);
return ret;
}
void dfs(int[] nums){
if(path.size()==nums.length){
// ret.add(path); // 这样不行,需要复制新的对象
ret.add(new ArrayList<>(path));
return;
}
for(int i=0;i<nums.length;i++){
if(!cheak[i]){ // 剪枝。已经用过的数字不能继续使用
path.add(nums[i]);
cheak[i] = true;
dfs(nums); // 递归调用
cheak[i] = false; // 回溯
path.remove(path.size()-1); // 回溯
}
}
}
}
13、子集
class Solution {
//全局变量的好处就在于,不需要复杂的传参
List<List<Integer>> ret;
List<Integer> path;
public List<List<Integer>> subsets(int[] nums) {
//位置连个引用变量分配内存
ret = new ArrayList<>();
path = new ArrayList<>();
//调用递归函数
dfs(nums,0);
return ret;
}
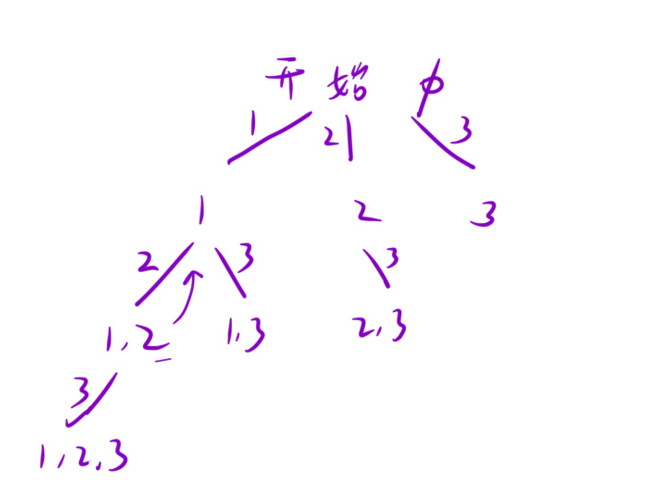
//算法一:从第0层开始,每一层的num[i]都面临选或者不选,最后的结果是一颗满二叉树,从根节点到达所有的接子节点的路径就是我们的答案,也就是说每一个叶子节点代表一个子集。
public void dfs1(int[] nums,int index){
if(index==nums.length){
//从始至终就只有一个path,如果不复制path,那么在添加时是正确的,之后会被该改变,最后回溯到根节点,所有之前添加的path都同时变成了null
ret.add(new ArrayList<>(path));
return ;
}
//不选
dfs(nums,index+1);
//选择
path.add(nums[index]);
dfs(nums,index+1);
//回溯
path.remove(path.size()-1);
}
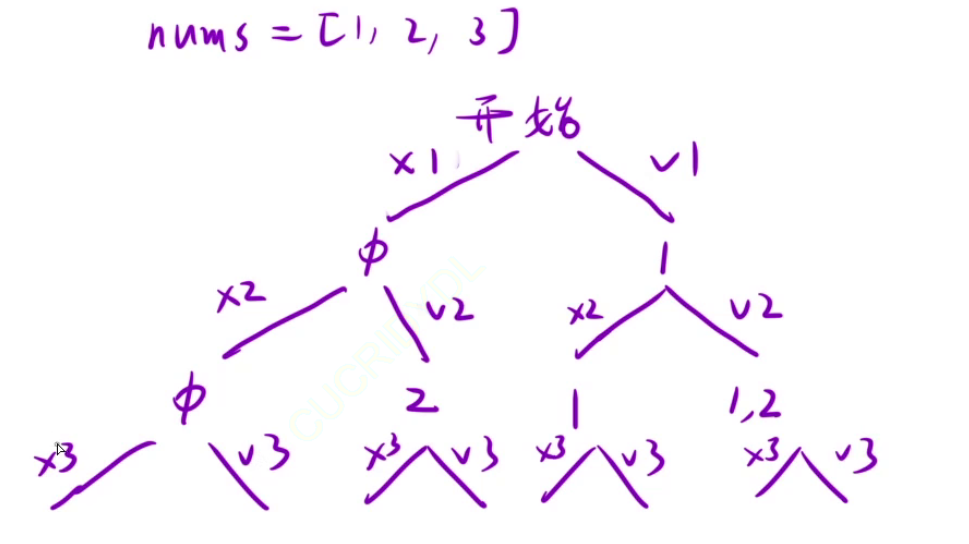
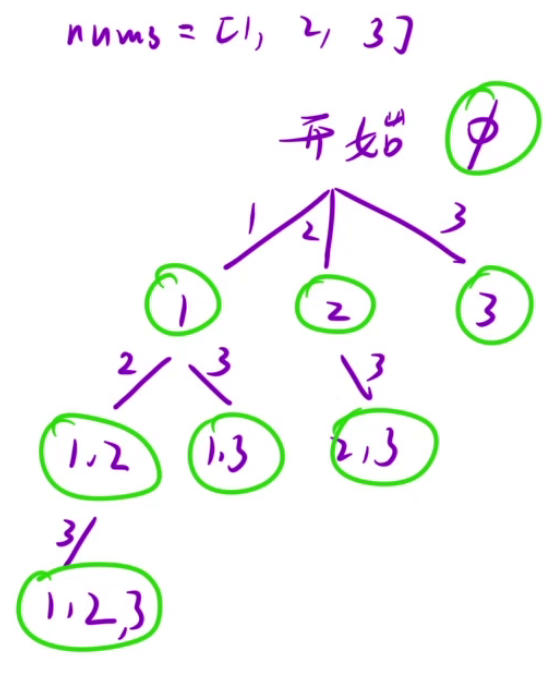
//算法二:对于任何一个节点node,我们只能选择节点代表的路径path的最后一个元素(不包含该元素)到nums的最后一个元素之间的一个元素。这种决策树的每一个节点都代表一个结果,算法二明显优于算法一。
public void dfs(int[] nums,int index){
//不选择,我需要把当前节点代表的子集加入到ret里面
ret.add(new ArrayList<>(path));
//选择
for(int i=index;i<nums.length;i++){
path.add(nums[i]);
dfs(nums,i+1);
path.remove(path.size()-1);
}
}
}
class Solution {
List<List<Integer>> ret;
List<Integer> subset;
public List<List<Integer>> subsets(int[] nums) {
ret = new ArrayList<>();
subset = new ArrayList<>();
dfs(nums,0);
return ret;
}
void dfs(int[] nums,int index){
// ret.add(new ArrayList<>(subset)); 如果写在这里就不用对空集特殊处理了
for(int i=index;i<nums.length;i++){
subset.add(nums[i]);
// 下面这一句写在这里好理解一些
ret.add(new ArrayList<>(subset));
dfs(nums,i+1);
subset.remove(subset.size()-1);
}
}
}
// 决策树
// ( )
// 1 2 3
// 2 3 3
// 3
// 决策树
// ()
// () 1
// () 2 () 2
// () 3 () 3 () 3 () 3
// 一共有nums.length层
解法二更优秀一些
四、综合练习
14、找出所有子集的异或总和再求和
class Solution {
int ret=0;// 返回值
int subset=0;//子集所有元素进行异或
public int subsetXORSum(int[] nums) {
dfs(nums,0);
return ret;
}
void dfs(int[] nums,int index){
ret+=subset;
for(int i=index;i<nums.length;i++){
subset^=nums[i];
dfs(nums,i+1);//这里是i+1,不是index+1;
subset^=nums[i];
}
}
}
根据题目意思需要求集合的所有子集,采用上题的方法二
15、全排列II ★★★(去重 —>排序去重法)
class Solution {
List<List<Integer>> ret;
List<Integer> path;
boolean[] cheak;
public List<List<Integer>> permuteUnique(int[] nums) {
ret = new ArrayList<>();
path = new ArrayList<>();
cheak = new boolean[nums.length];
Arrays.sort(nums);
dfs(nums);
return ret;
}
public void dfs(int[] nums){
if(path.size()==nums.length){
ret.add(new ArrayList<>(path));
return;
}
for(int i=0;i<nums.length;i++){
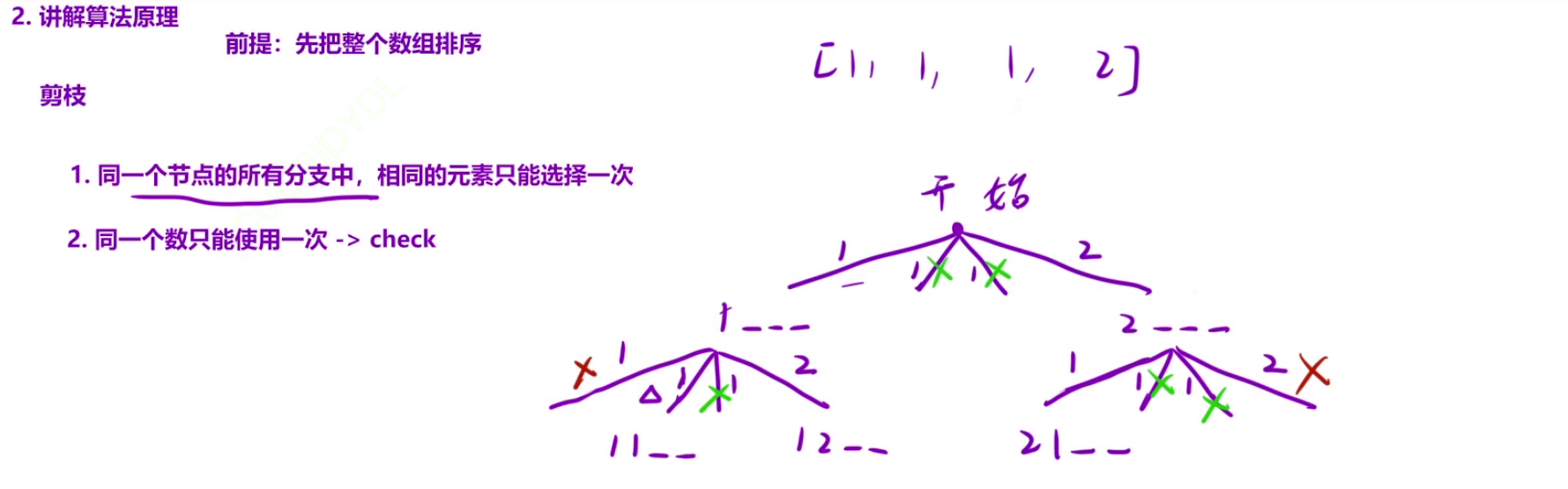
// 关注不合法的情况
// 剪枝
if(cheak[i]==true|| (i!=0&&nums[i]==nums[i-1]&&cheak[i-1]==false)){
continue;
}
// 关注合法的情况 ture改成false,&&改成||,||改成&& 全部相反即可
// if(cheak[i]==false && (i==0||nums[i]!=nums[i-1] || cheak[i-1]==true{
path.add(nums[i]);
cheak[i]=true;
dfs(nums);
path.remove(path.size()-1);
cheak[i]=false;
// }
}
}
}
如何让去重:可以先对数组进行排序
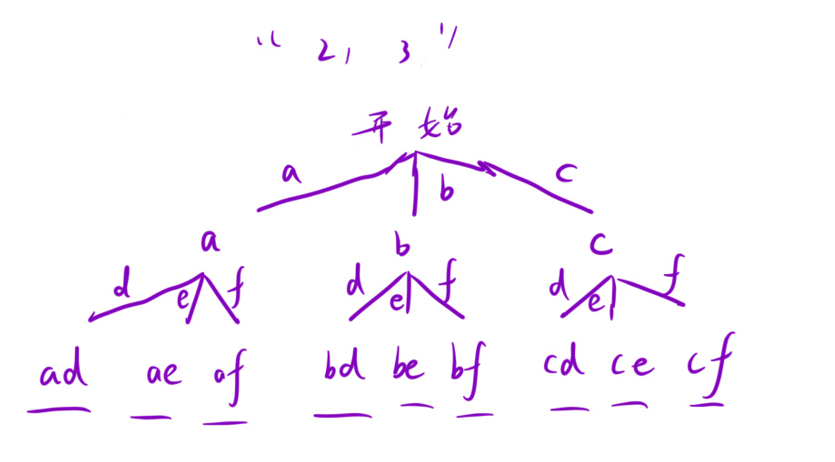
16、电话号码的字母组合数
class Solution {
String[] str={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
List<String> ret;
StringBuffer path;
public List<String> letterCombinations(String digits){
ret = new ArrayList<>();
path = new StringBuffer();
if(digits.equals("")) return ret;
dfs(digits,0);
return ret;
}
void dfs(String digits,int index){
// 根据题意,当解析出来的字符串长度等于
if(path.length() == digits.length()){
ret.add(path.toString());
return ;
}
// 根据号码取字符串
int i = digits.charAt(index)-'0';
String s = str[i];
// dfs
for(char ch:s.toCharArray()){
path.append(ch);
dfs(digits,index+1);
path.deleteCharAt(path.length()-1);
}
}
}
digits.lengt()=N
其实就是N重循环,但是不可能真的写的N层for循环而是写递归调用。
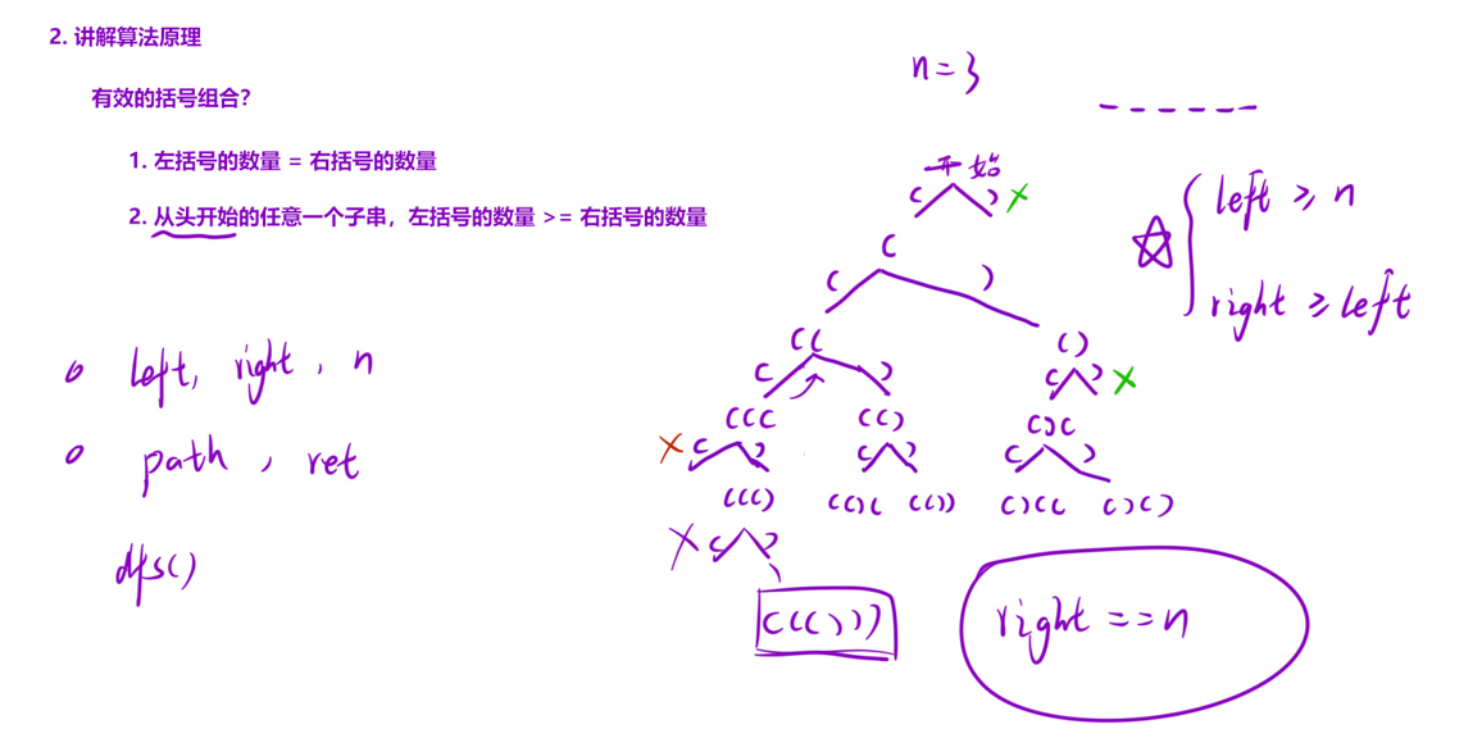
17、括号生成
class Solution {
List<String> ret;
StringBuffer path;
int left = 0;
int right = 0;
int length;
public List<String> generateParenthesis(int n) {
length = 2*n;
ret = new ArrayList<>();
path = new StringBuffer();
dfs(n);
return ret;
}
void dfs(int n){
if(path.length()==length){
ret.add(path.toString());
return ;
}
// 加左边括号
if(n>0){
path.append('(');
left++;
dfs(n-1);
left--;
path.deleteCharAt(path.length()-1);//回溯
}
// 当右括号多与左括号时才能加左括号
if(left>right){
path.append(')');
right++;
dfs(n);
right--;
path.deleteCharAt(path.length()-1);//回溯
}
}
}
决策树:如果n>0,则可以加左括号;如果left>right,则可以加右括号。
当path的长度等于2*n时,说明找到了一种生成方式,加入到ret中
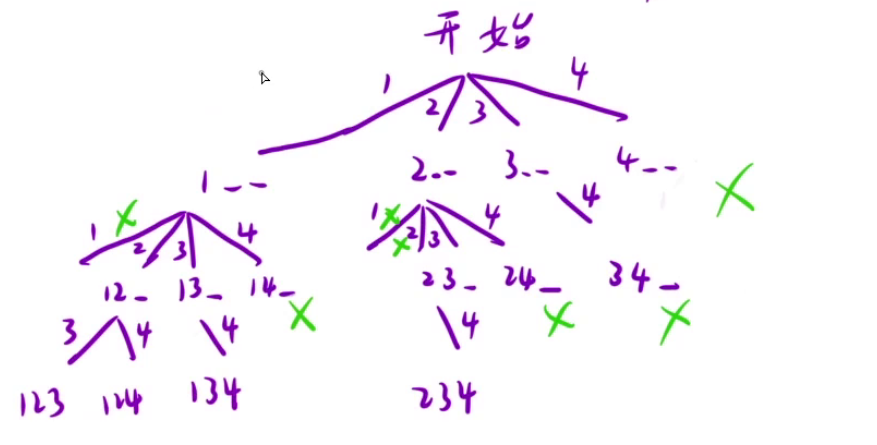
18、组合
class Solution {
List<List<Integer>> ret;
List<Integer> subset;
public List<List<Integer>> combine(int n, int k) {
ret = new ArrayList<>();
subset = new ArrayList<>();
dfs(1,n,k);
return ret;
}
// start:从index位置开始遍历
// n:[1~n]的组合
// k:组合长度为k
void dfs(int start,int n,int k){
if(subset.size() == k){
ret.add(new ArrayList<>(subset));
return ;
}
// 只枚举更大的数子
for(int i=start;i<=n;i++){
subset.add(i);
dfs(i+1,n,k);
subset.remove(subset.size()-1);
}
}
}
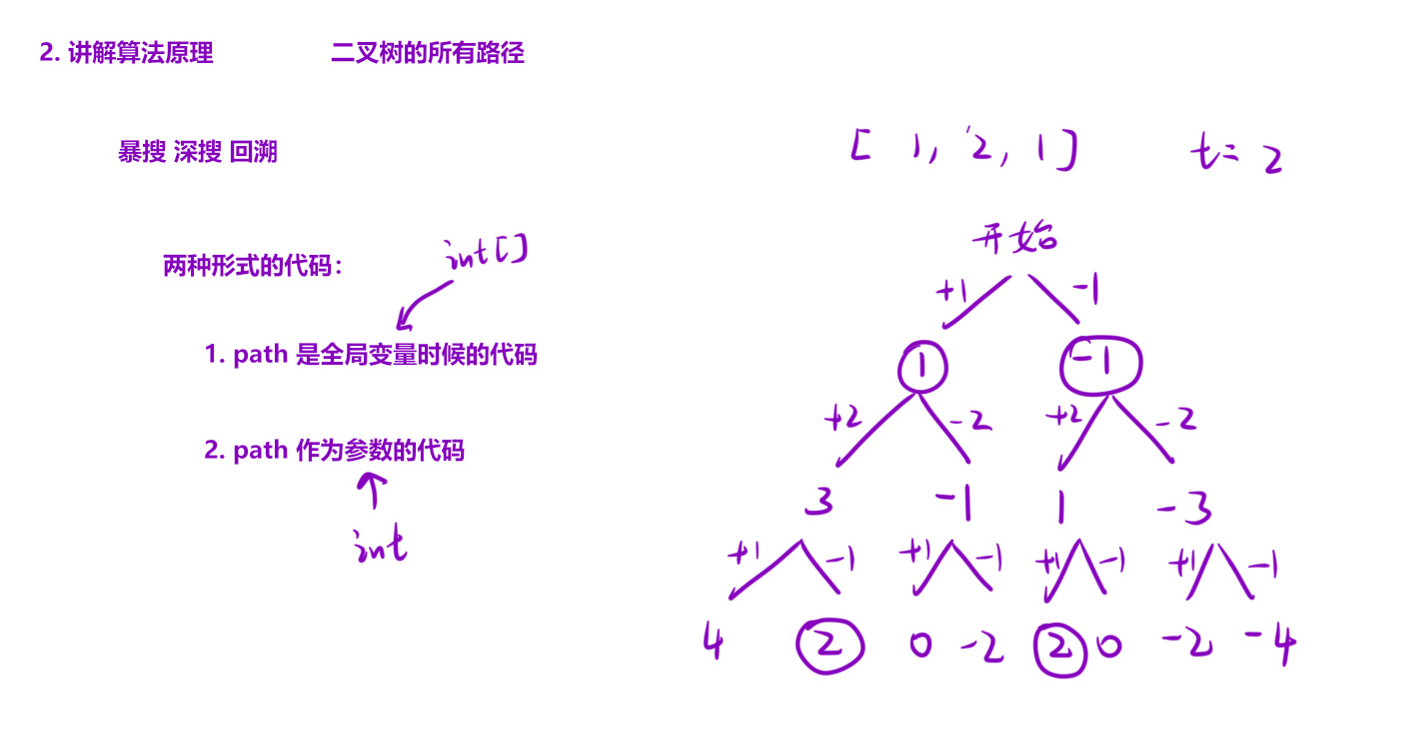
19、目标和
class Solution {
int ret;
int target;
int sum;
public int findTargetSumWays(int[] nums, int _target) {
target = _target;
dfs(nums,0);
return ret;
}
void dfs(int[] nums,int index){
if(index == nums.length){
if(sum==target) ret++;
return ;
}
// +
sum+=nums[index];
dfs(nums,index+1);
sum-=nums[index];
// -
sum-=nums[index];
dfs(nums,index+1);
sum+=nums[index];
}
}
// 此时对于全局变量必须要搞对称操作进行回复现场
class Solution {
int ret;
int target;
public int findTargetSumWays(int[] nums, int _target) {
target = _target;
dfs(nums,0,0);
return ret;
}
void dfs(int[] nums,int index,int sum){
if(sum==target&&index == nums.length){
ret++;
return ;
}
if(index == nums.length) return ;
// +
dfs(nums,index+1,sum+nums[index]);
// -
dfs(nums,index+1,sum-nums[index]);
}
}
// 只要能实现恢复现场即可,因为函数内部并没有修改sum,
// 被调函数也不会改变sum的值,因此无需恢复现场
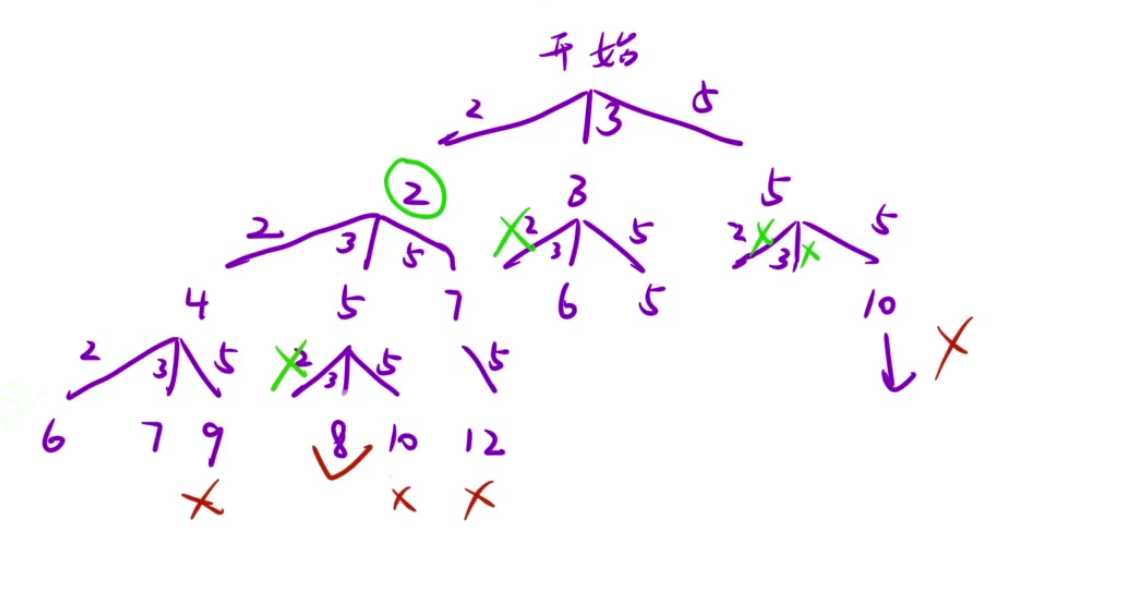
20、组合总和★★★★根据决策树写代码
class Solution {
List<List<Integer>> ret;
List<Integer> path;
int sum;
int aim;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
ret = new ArrayList<>();
path = new ArrayList<>();
aim = target;
// 先排序,否则不能利用单调性进行剪枝
Arrays.sort(candidates);
dfs(candidates,0);
return ret;
}
void dfs(int[] candidates,int start){
if(sum == aim){
ret.add(new ArrayList<>(path));
return ;
}
// 剪枝一:遍历的顺序从strat开始进行去重
for(int i=start;i<candidates.length;i++){
// 剪枝二,利用单调性可得后续的sum也大于aim
if(sum+candidates[i]>aim) break;
sum+=candidates[i];
path.add(candidates[i]);
dfs(candidates,i);// 注意此处传参为i,而不是start
path.remove(path.size()-1);
sum-=candidates[i];
}
}
}
枚举策略:num[i]使用多少个
class Solution {
int aim;
List<Integer> path;
List<List<Integer>> ret;
public List<List<Integer>> combinationSum(int[] nums, int target) {
path = new ArrayList<>();
ret = new ArrayList<>();
aim = target;
dfs(nums, 0, 0);
return ret;
}
public void dfs(int[] nums, int pos, int sum) {
if (sum == aim) {
ret.add(new ArrayList<>(path));
return;
}
if (sum > aim || pos == nums.length)
return;
// 枚举 nums[pos] 使⽤多少个
for (int k = 0; k * nums[pos] + sum <= aim; k++) {
if (k != 0)
path.add(nums[pos]);
dfs(nums, pos + 1, sum + k * nums[pos]);
}
// 恢复现场
for (int k = 1; k * nums[pos] + sum <= aim; k++) {
path.remove(path.size() - 1);
}
}
}
只要决策树正确,跟着决策树写代码即可,没固定模板
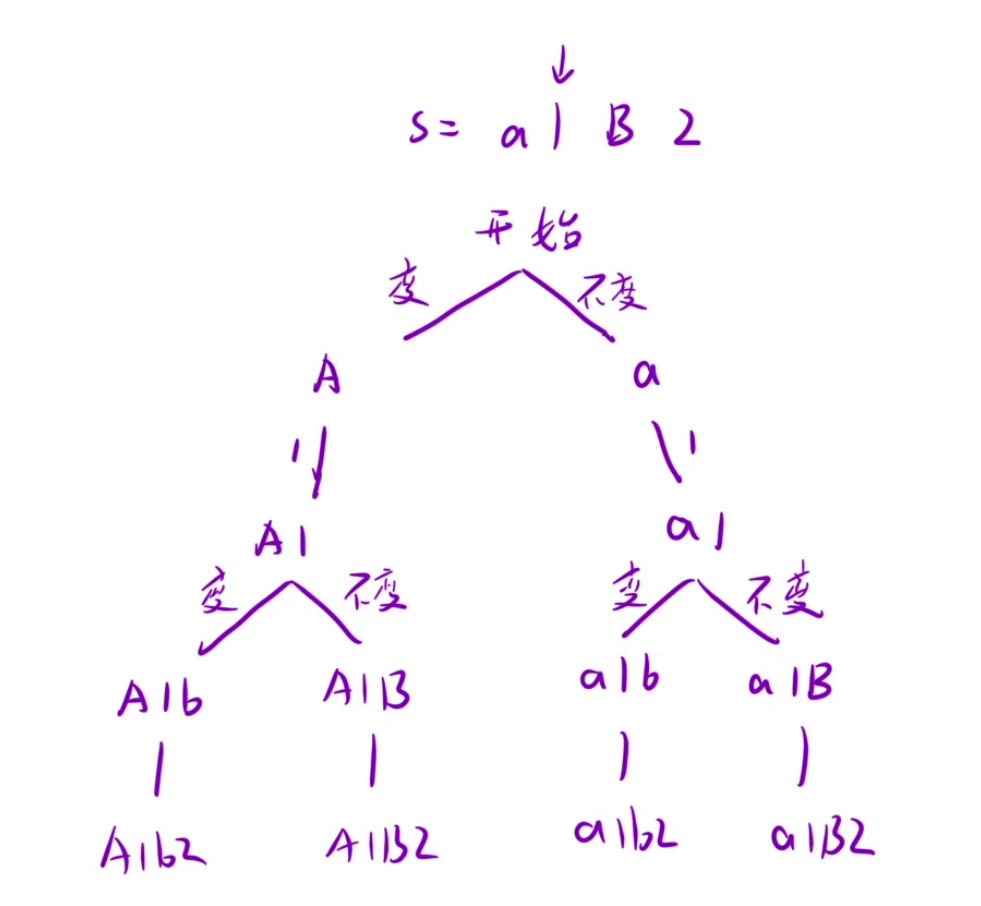
21、字母大小写全排列
class Solution {
List<String> ret;
StringBuffer path;
public List<String> letterCasePermutation(String s) {
ret = new ArrayList<>();
path = new StringBuffer();
dfs(s, 0);
return ret;
}
void dfs(String s, int index) {
if (path.length() == s.length()) {
ret.add(path.toString());
return;
}
char ch = s.charAt(index);
if ('0' <= ch && ch <= '9') {
path.append(ch);
dfs(s,index+1);
path.deleteCharAt(path.length() - 1);// 也要恢复现场
}else{
// ch保持不变
path.append(ch);
dfs(s, index + 1);
path.deleteCharAt(path.length() - 1);
// ch大小写转换
path.append(fun(ch));
dfs(s, index + 1);
path.deleteCharAt(path.length() - 1);
}
}
char fun(char c){
if('a'<=c &&c<='z'){
return Character.toUpperCase(c);
}
return Character.toLowerCase(c);
}
}
// 我将所有子串分成了三类
class Solution {
StringBuffer path;
List<String> ret;
public List<String> letterCasePermutation(String s) {
path = new StringBuffer();
ret = new ArrayList<>();
dfs(s, 0);
return ret;
}
public void dfs(String s, int pos) {
if (pos == s.length()) {
ret.add(path.toString());
return;
}
char ch = s.charAt(pos);
// 不改变
path.append(ch);
dfs(s, pos + 1);
path.deleteCharAt(path.length() - 1); // 恢复现场
// 改变
if (ch < '0' || ch > '9') {
char tmp = change(ch);
path.append(tmp);
dfs(s, pos + 1);
path.deleteCharAt(path.length() - 1); // 恢复现场
}
}
public char change(char ch) {
if (ch >= 'a' && ch <= 'z')
return ch -= 32;
else
return ch += 32;
}
}
// 吴老师代码是分两种情况考虑的
22、优美的排列
class Solution {
int ret;
boolean[] cheak;
public int countArrangement(int n) {
cheak = new boolean[n+1];
dfs(1,n);
return ret;
}
void dfs(int m,int n){
if(m == n+1){
ret++;
return;
}
for(int i=1;i<=n;i++){
if(!cheak[i]&&(i%m==0||m%i==0)){
cheak[i] = true;
dfs(m+1,n);
cheak[i] = false;
}
}
}
}
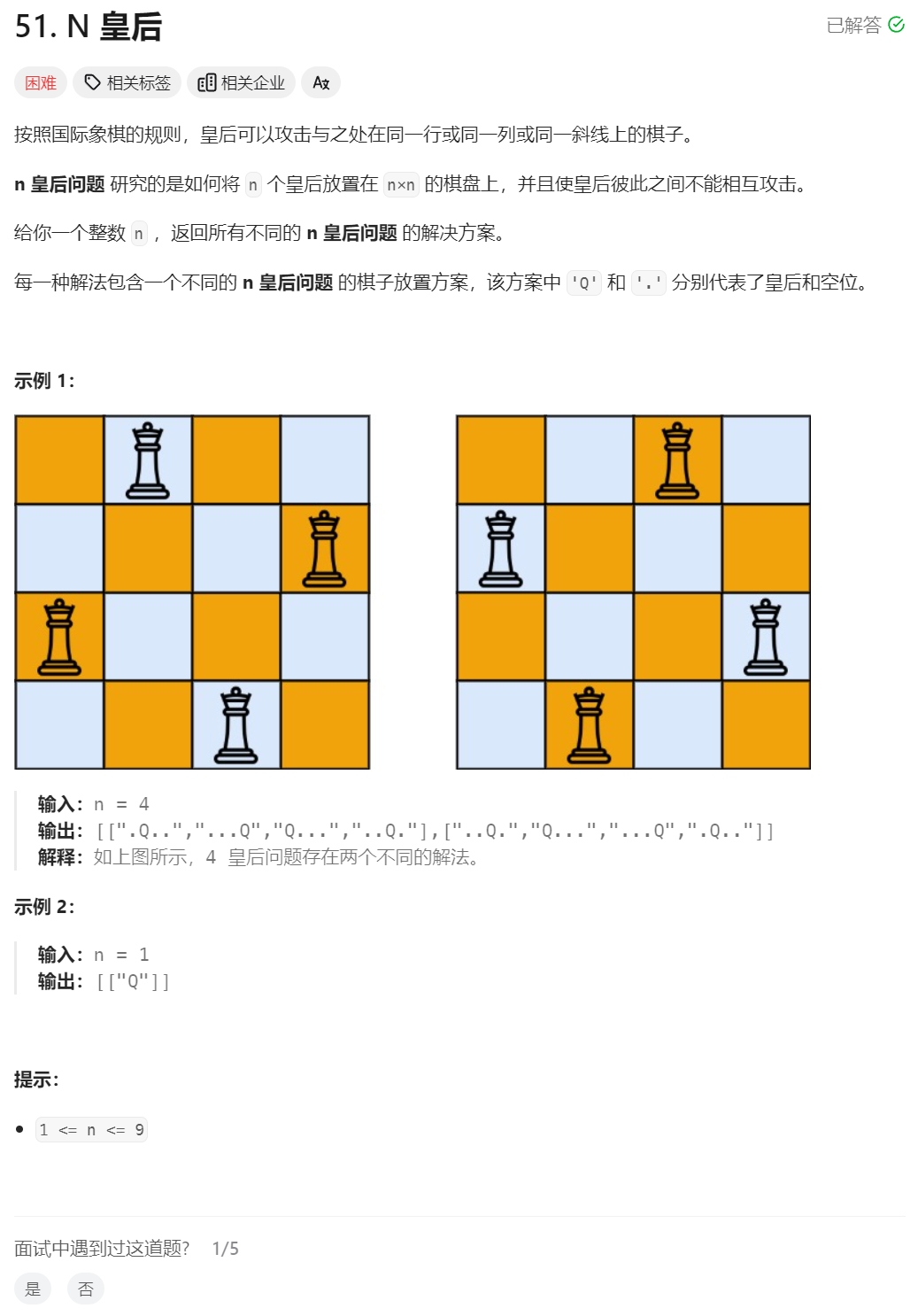
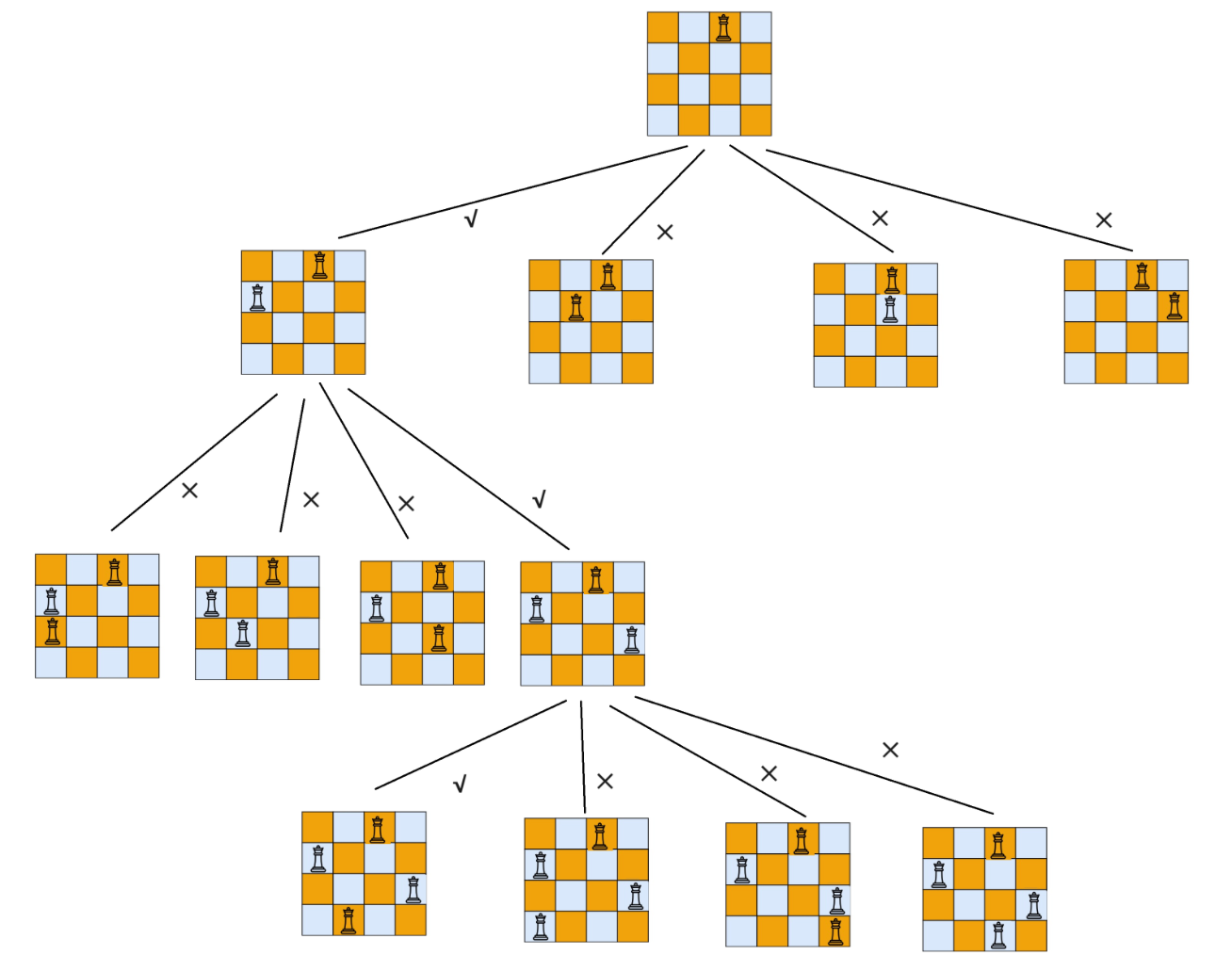
23、N皇后问题(以空间换时间)
class Solution {
List<List<String>> ret;
List<String> path;
List<Integer> row;
List<Integer> col;
int n;
public List<List<String>> solveNQueens(int _n) {
ret = new ArrayList<>();
path = new ArrayList<>();
row = new ArrayList<>();
col = new ArrayList<>();
n = _n;
dfs(0);
return ret;
}
void dfs(int m){
if(m==n){
ret.add(new ArrayList<>(path));
return ;
}
StringBuffer temp = new StringBuffer();
for(int i=0;i<n;i++) temp.append(".");
for(int i=0;i<n;i++){
if(m==0 || cheak(m,i)){
temp.setCharAt(i,'Q');
path.add(temp.toString());
row.add(m);
col.add(i);
dfs(m+1);
col.remove(col.size()-1);
row.remove(row.size()-1);
path.remove(path.size()-1);
temp.setCharAt(i,'.');
}
}
}
boolean cheak(int x,int y){
for(int i=0;i<x;i++){
int a=row.get(i);
int b=col.get(i);
if(a-x==b-y || a-x==y-b || b == y) return false;
}
return true;
}
}
怎么优化呢?
class Solution {
List<List<String>> ret;
char[][] path;// 棋盘
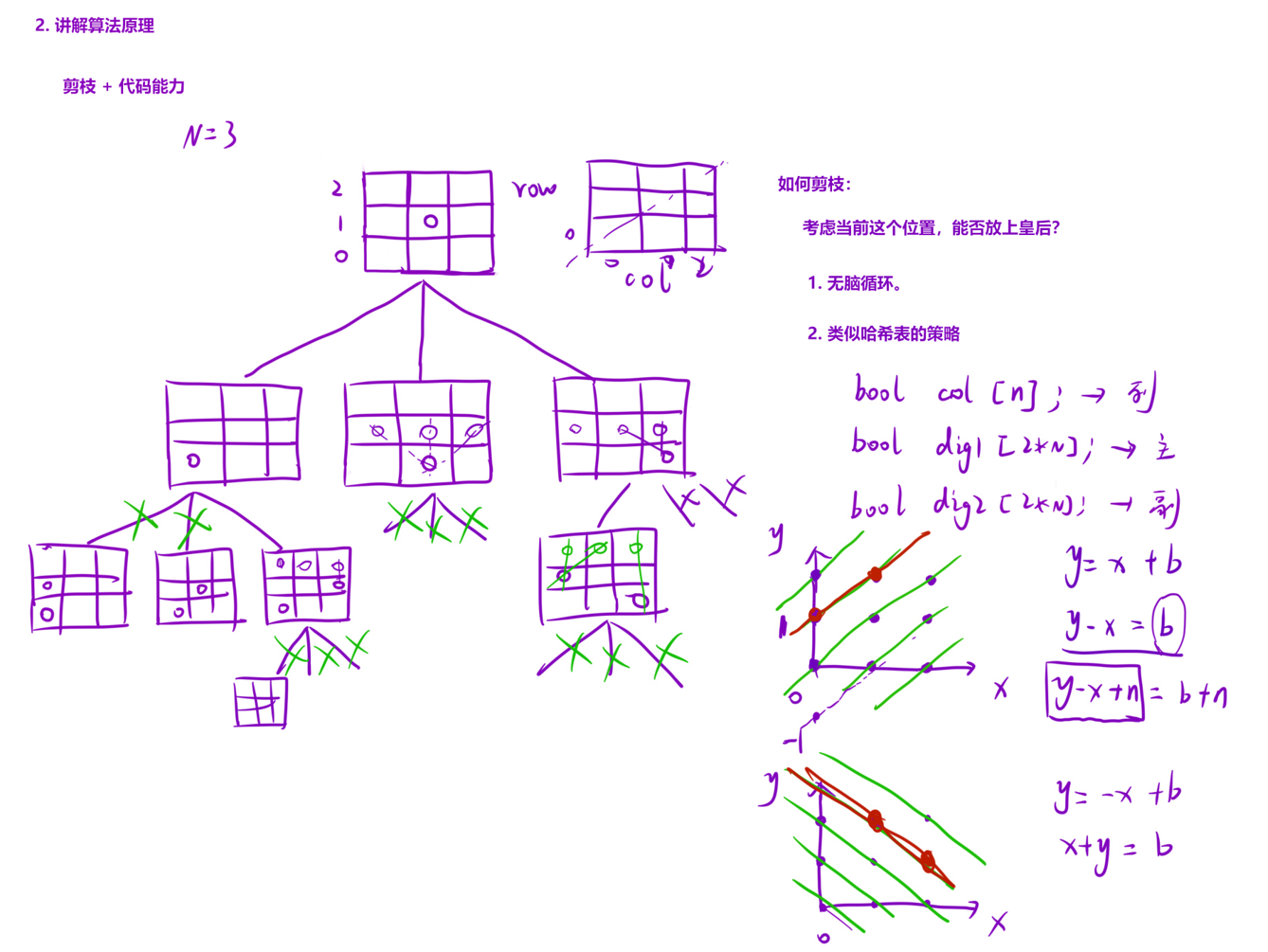
boolean[] col;// 判断这一列是否使用过
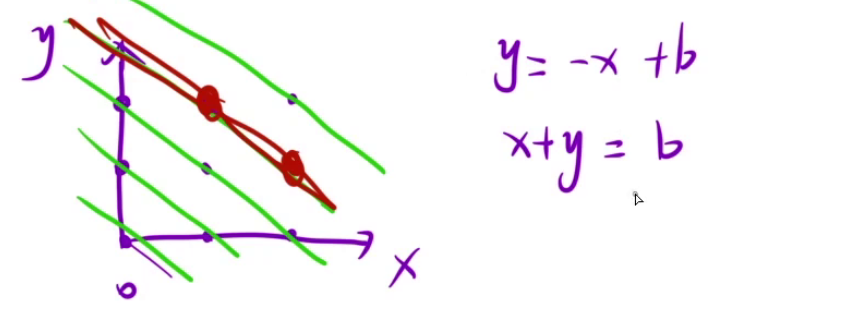
boolean[] dig1;// 判断主对角线是否使用过
boolean[] dig2;// 判断副对角线是否使用过
public List<List<String>> solveNQueens(int n) {
ret = new ArrayList<>();
path = new char[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
path[i][j]='.';
}
}
col = new boolean[n];
dig1 = new boolean[2*n];
dig2 = new boolean[2*n];
dfs(n,0);
return ret;
}
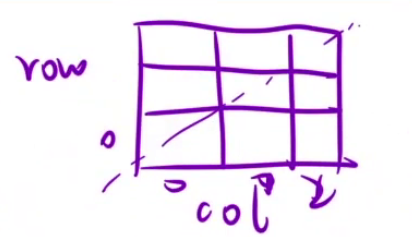
public void dfs(int n,int y){
if(y==n){
List<String> list = new ArrayList<>();
for(int i=0;i<n;i++){
list.add(new String(path[i]));
}
ret.add(list);
// return ;
}
//第index行有n个空格
for(int x=0;x<n;x++){
if(col[x]==false&&dig1[y-x+n]==false&&dig2[y+x]==false){
path[y][x]='Q';
col[x]=true;
dig1[y-x+n]=true;
dig2[y+x]=true;
dfs(n,y+1);
col[x]=false;
dig1[y-x+n]=false;
dig2[y+x]=false;
path[y][x]='.';
}
}
}
}
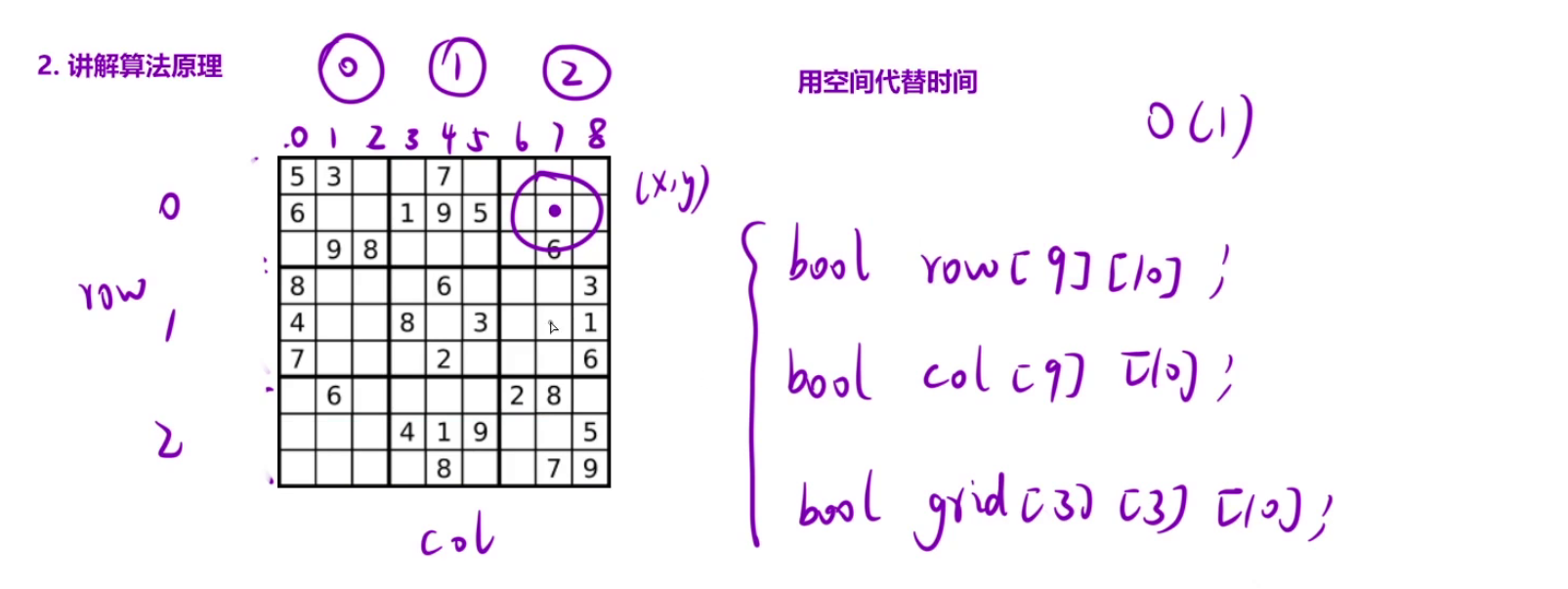
24、有效的数独 (以空间换时间)
class Solution {
boolean[][] row,col;
boolean[][][] gird;
public boolean isValidSudoku(char[][] board) {
// 两个二维数组是为了判断某一行和某一列是否有效
// 三维数组是为了判断九个九宫格是有效
// 这里开辟十个空间是为了下标与数字对应
row = new boolean[9][10];// 例:row[0][1]=true代表第0行存在1
col = new boolean[9][10];// 例:col[0][2]=true代表第0列存在2
gird = new boolean[3][3][10];// 例:gird:[0][0][4]=true代表第0个小宫存在4
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]=='.'){
continue;
}
int num=board[i][j]-'0';
if(row[i][num]==false&&col[j][num]==false&&
gird[i/3][j/3][num]==false){
row[i][num]=true;
col[j][num]=true;
gird[i/3][j/3][num]=true;
}
else{
return false;
}
}
}
return true;
}
}
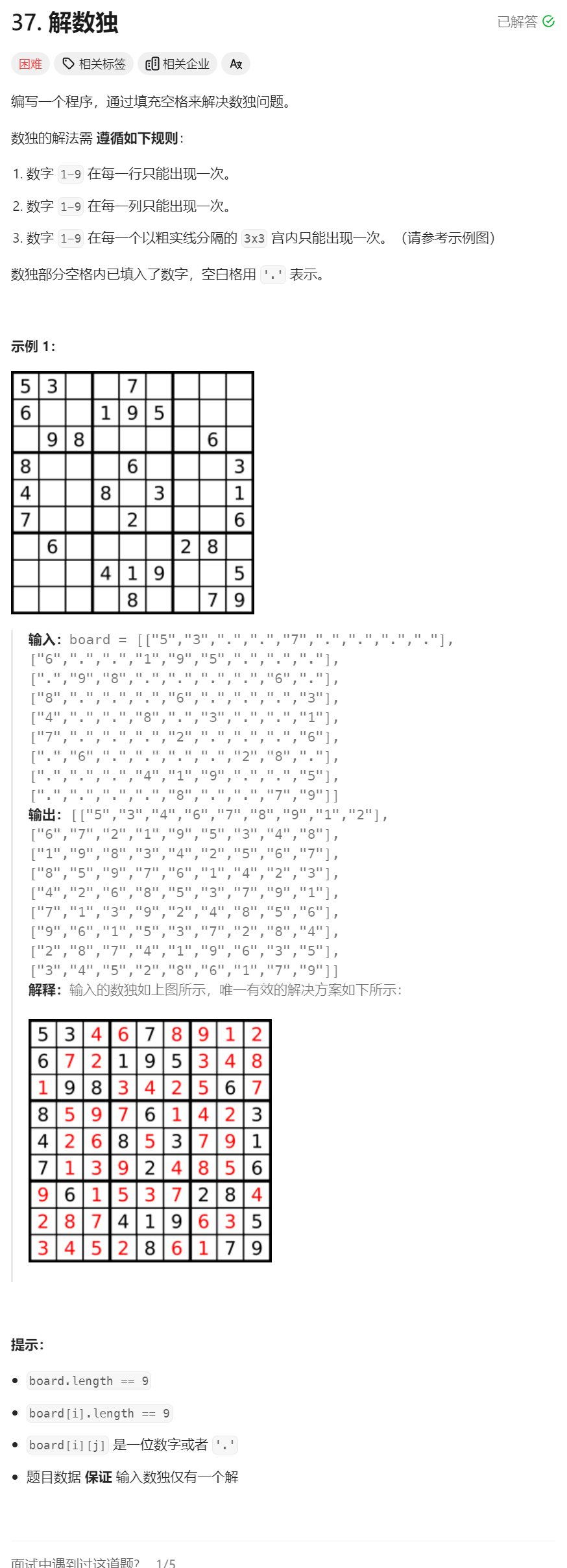
25、解数独
class Solution {
char[] nums;
char[][] ret = new char[9][9];
public void solveSudoku(char[][] board) {
nums = "123456789".toCharArray();
dfs(board,0);
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
board[i][j]=ret[i][j];
}
}
}
void dfs(char[][] board,int n){
if(n==81){
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
ret[i][j]=board[i][j];
}
}
return;
}
int x = n/9;
int y = n%9;
if(board[x][y]!='.' ){
dfs(board,n+1);
}else{
for(char c:nums ){
if(fun(board,x,y,c)){
board[x][y]=c;
dfs(board,n+1);
board[x][y]='.';
}
}
}
}
// 判断(x,y)位置是否可以填入c,时间复杂度为O(27)
boolean fun(char[][] board,int x,int y,char c){
int m = x/3;
int n = y/3;
for(int i=3*m;i<3*m+3;i++){
for(int j=3*n;j<3*n+3;j++){
if(board[i][j]==c) return false;
}
}
for(int i=0;i<9;i++){
if(board[x][i]==c) return false;
if(board[i][y]==c) return false;
}
return true;
}
}
class Solution {
//直接修改二维数组
boolean[][] col,row;
boolean[][][] grid;
char[][] temp;
boolean flag=false;
public void solveSudoku(char[][] board) {
// 三兄弟在填写的时候用于判断某个数字是否合法,添加数字后需要更三兄弟,还要牵扯到回溯
col = new boolean[9][10];
row = new boolean[9][10];
grid = new boolean[3][3][10];
temp = new char[9][9];
//初始化一下三兄弟
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]!='.'){
int num = board[i][j]-'0';
row[i][num]=true;
col[j][num]=true;
grid[i/3][j/3][num]=true;
}
}
}
// (0,0)下标开始。这参数设置的不如我的n,当n==81时,说明找到了答案
dfs(board,0,0);
// for(int s=0;s<9;s++){
// for(int k=0;k<9;k++){
// board[s][k]=temp[s][k];
// }
// }
}
public void dfs(char[][] board,int i,int j){
if(i==9){
// 如何保存返回值,如果不进行回溯的话,board数组会在回溯的变成初始的样子
// 保存返回值的第一种方法就是对结果进行复制
// for(int s=0;s<9;s++){
// for(int k=0;k<9;k++){
// temp[s][k]=board[s][k];
// }
// }
flag = true;
}
// 题目保证有且仅有一个解,所以当找到答案时可以直接一路返回无需回溯
if(flag) return;// 已找到答案,所以return
if(board[i][j]=='.'){
for(int k=1;k<=9;k++){
if(row[i][k]==false&&col[j][k]==false&&grid[i/3][j/3][k]==false){
board[i][j]=(char)(48+k);
row[i][k]=true;
col[j][k]=true;
grid[i/3][j/3][k]=true;
if(j==8){
dfs(board,i+1,0);
}else{
dfs(board,i,j+1);
}
// 题目保证有且仅有一个解,所以当找到答案时可以直接一路返回无需回溯
if(flag) return;// 防止回溯,所以return
// 回溯操作
board[i][j]='.' ;
row[i][k]=false;
col[j][k]=false;
grid[i/3][j/3][k]=false;
}
}
}
else{
if(j==8){
dfs(board,i+1,0);
}else{
dfs(board,i,j+1);
}
}
}
}
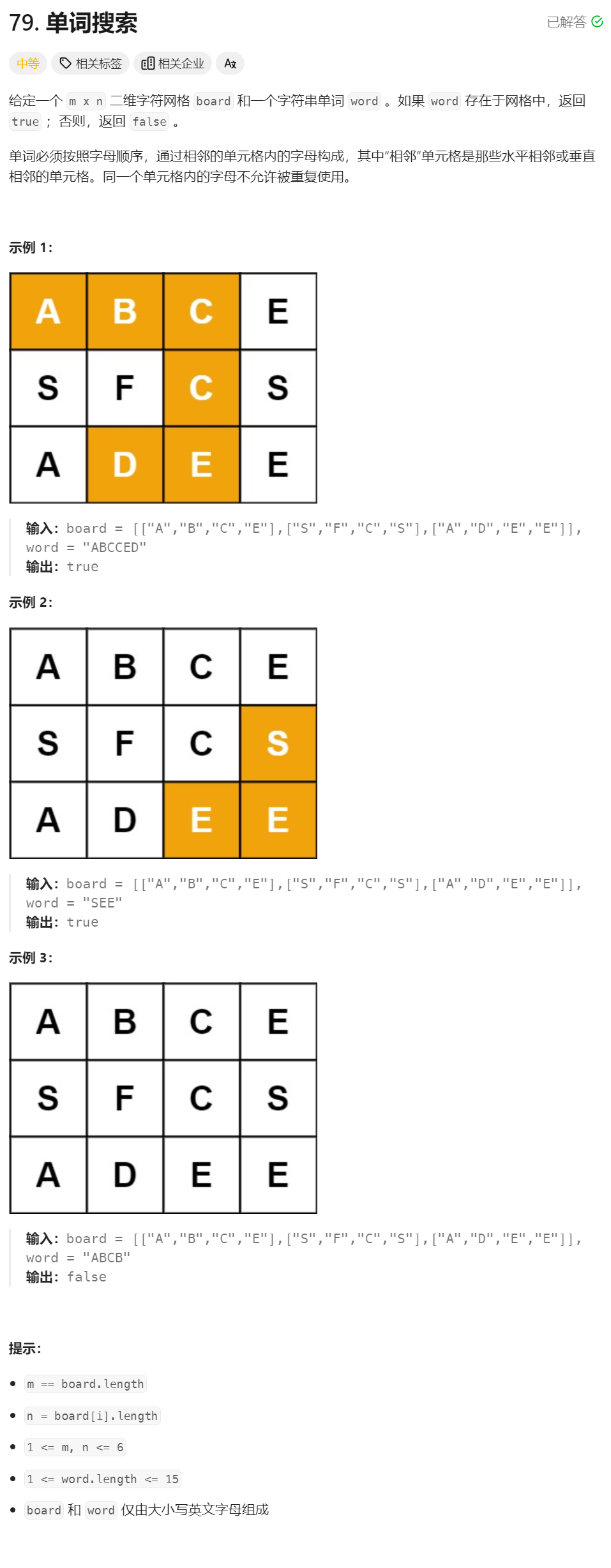
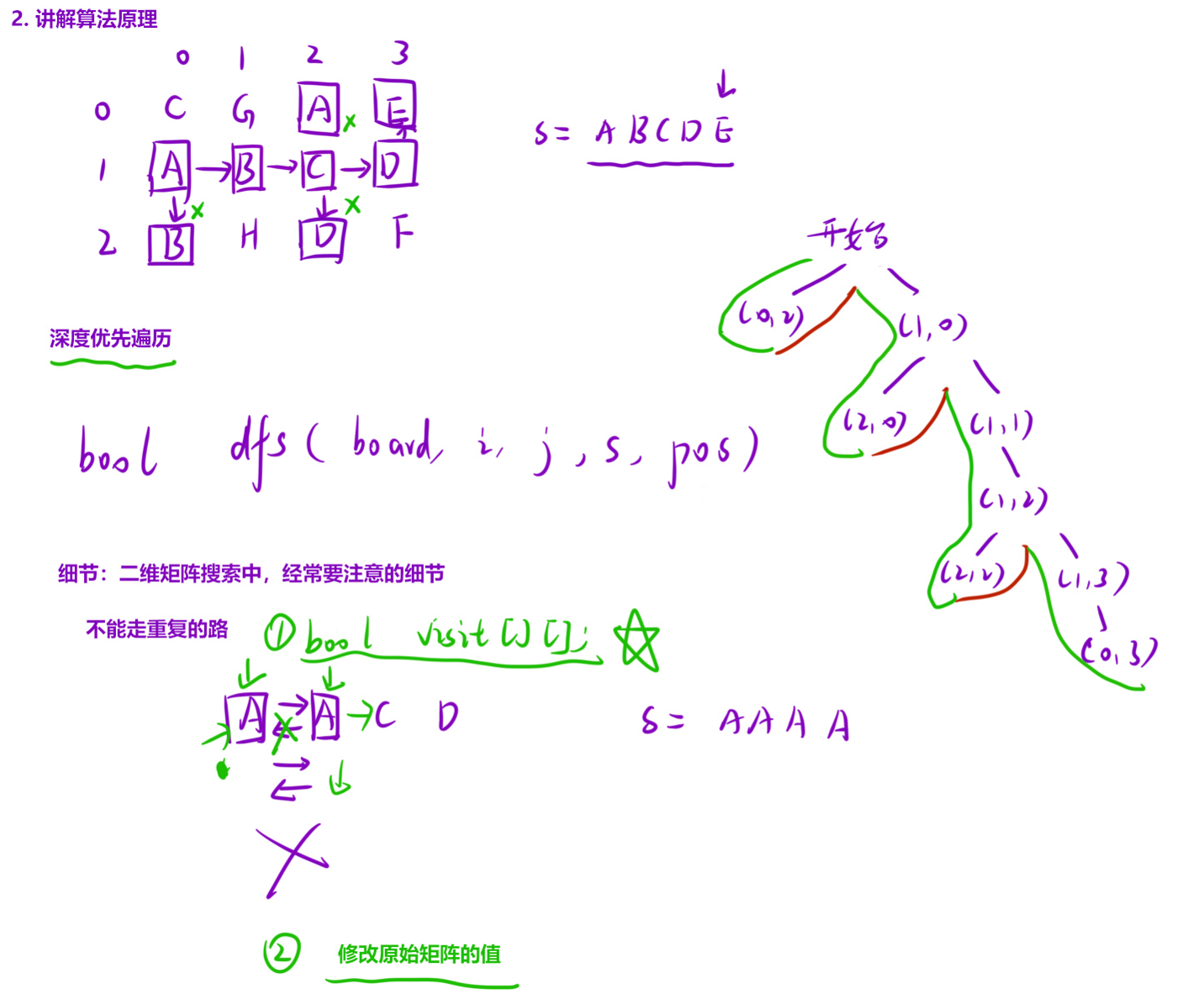
26、单词搜索 (dfs只能解决以某个起点为开始的问题,所以循环调用dfs)
class Solution {
boolean ret;
int[] dx = {0,0,-1,1};
int[] dy = {-1,1,0,0};
int m;
int n;
public boolean exist(char[][] board, String word) {
m = board.length;
n = board[0].length;
boolean[][] cheak = new boolean[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
// 每次dfs都会将cheak回溯到初始状态,不影响下一次dfs
dfs(board,i,j,word,0,cheak);
if(ret) break;
}
}
return ret;
}
void dfs(char[][] board,int x,int y,String word,int index,boolean[][] cheak){
if(ret) return ;
if(cheak[x][y]==false && board[x][y]==word.charAt(index)){
cheak[x][y] = true;
index++;
if(index==word.length()){
ret = true;
return ;
}
for(int i=0;i<4;i++){
int a = x+dx[i];
int b = y+dy[i];
if(a>=0&&a<m&&b>=0&&b<n&&cheak[a][b]==false)
dfs(board,a,b,word,index,cheak);
}
// 没有在回溯之前返回,所以会回溯
if(ret) return;
cheak[x][y] = false;
index--;
}
}
}
class Solution {
boolean flag=false;
public boolean exist(char[][] board, String word) {
int m=board.length;
int n=board[0].length;
char[][] temp = new char[m+2][n+2];
boolean[][] cheak = new boolean[m+2][n+2];
for(int i=0;i<m+2;i++){
for(int j=0;j<n+2;j++){
if(i==0||j==0||i==m+1||j==n+1){
temp[i][j]='0';
cheak[i][j]=true;
}else{
temp[i][j]=board[i-1][j-1];
cheak[i][j]=false;
}
}
}
char[] arr = word.toCharArray();
for(int i=1;i<=m+1;i++){
for(int j=1;j<=n+1;j++){
dfs(temp,0,arr,i,j,cheak);
if(flag) return true;
}
}
return flag;
}
public void dfs(char[][] temp,int index,char[] arr,int row,int col,boolean[][] cheak){
int m=temp.length;
int n=temp[0].length;
if(index==arr.length){
flag=true;
return ;
}
if(flag) return;
if(cheak[row][col]==true){
return ;
}
if(temp[row][col]==arr[index]){
cheak[row][col]=true;
dfs(temp,index+1,arr,row-1,col,cheak);
dfs(temp,index+1,arr,row,col+1,cheak);
dfs(temp,index+1,arr,row+1,col,cheak);
dfs(temp,index+1,arr,row,col-1,cheak);
cheak[row][col]=false;
return ;
}
}
}
class Solution {
boolean[][] vis;
int m, n;
char[] word;
public boolean exist(char[][] board, String _word) {
m = board.length;
n = board[0].length;
word = _word.toCharArray();
vis = new boolean[m][n];
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++) {
if (board[i][j] == word[0]) {
vis[i][j] = true;
if (dfs(board, i, j, 1))
return true;
vis[i][j] = false;
}
}
return false;
}
int[] dx = { 0, 0, 1, -1 };
int[] dy = { 1, -1, 0, 0 };
public boolean dfs(char[][] board, int i, int j, int pos) {
if (pos == word.length) {
return true;
}
// 上下左右去匹配 word[pos]
// 利⽤向量数组,⼀个 for 搞定上下左右四个⽅向
for (int k = 0; k < 4; k++) {
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && board[x][y] == word[pos]) {
vis[x][y] = true;
if (dfs(board, x, y, pos + 1))
return true;
vis[x][y] = false;
}
}
return false;
}
}
27、黄金矿工★★★★
class Solution {
int m;
int n;
public int getMaximumGold(int[][] grid) {
m = grid.length;
n = grid[0].length;
int max = 0;
// dfs只能实现从一个坐标开始深度搜索找到从这个起点开始的最大值
// 因此要二重循环调用dfs取最大值
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]!=0)
max = Math.max(max,dfs(grid,i,j));
}
}
return max;
}
// 向量数组
int[] dx = { 0, 0, 1, -1 };
int[] dy = { 1, -1, 0, 0 };
// 从某个起点开始找最大值
int dfs(int[][] grid, int x, int y) {
int max = 0;
for (int i = 0; i < 4; i++) {
int a = x + dx[i];
int b = y + dy[i];
if (a >= 0 && a < m && 0 <= b && b < n && grid[a][b]!=0){
int temp = grid[x][y];
grid[x][y]=0;// 不要错写成grid[a][b];
max = Math.max(max,dfs(grid, a, b));
grid[x][y]=temp;
}
}
return grid[x][y] + max;
}
}
28、不同路径III
class Solution {
int ret;
int m;
int n;
int[] start;// 记录起点
int[] end;// 记录终点
int path=1;// 保证走遍所有的0
public int uniquePathsIII(int[][] grid) {
m = grid.length;
n = grid[0].length;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]==1) start = new int[]{i,j};
if(grid[i][j]==2) end = new int[]{i,j};
if(grid[i][j]==0) path++;
}
}
dfs(grid,start[0],start[1]);
return ret;
}
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
void dfs(int[][] grid,int x,int y){
if(end[0]==x&&end[1]==y&&path==0){
ret++;
return ;
}
for(int i=0;i<4;i++){
int a = x+dx[i];
int b = y+dy[i];
if(0<=a&&a<m&&0<=b&&b<n&&grid[a][b]!=-1){
int temp = grid[x][y];
grid[x][y] = -1;
path--;
dfs(grid,a,b);
path++;
grid[x][y] = temp;
}
}
}
}
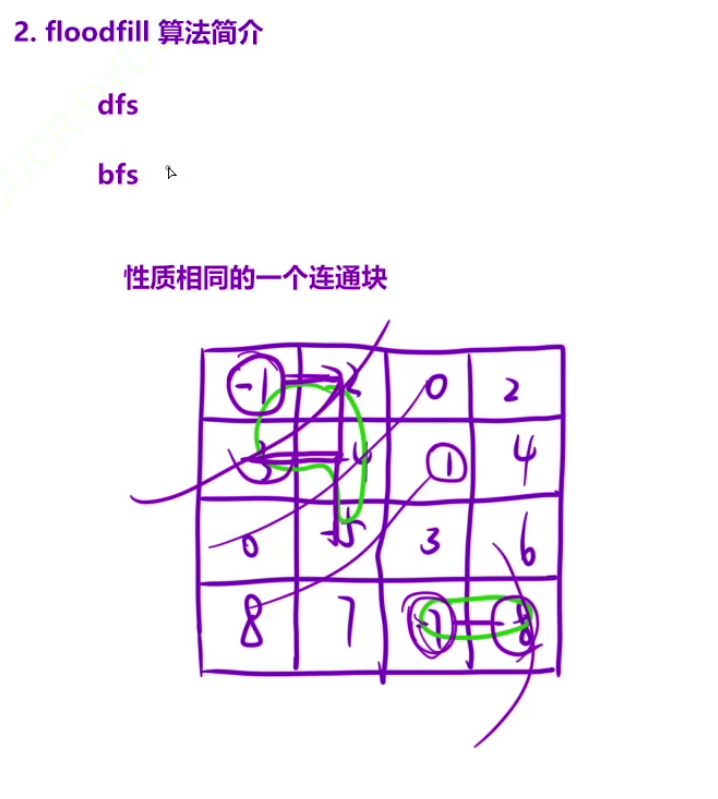
五、FloodFill 算法
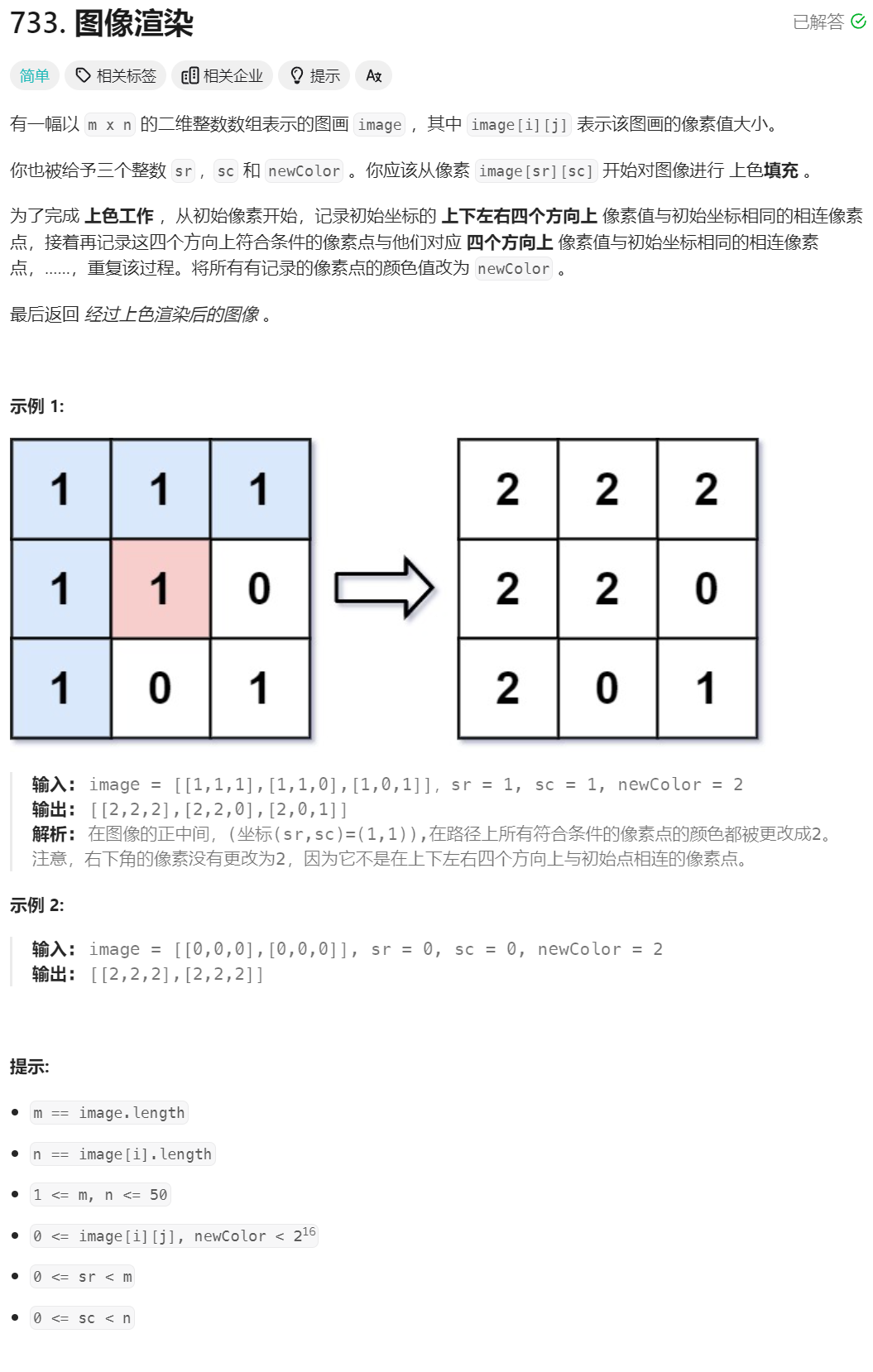
29、图像渲染
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
// 宽度优先遍历
int prev = image[sr][sc];
if (prev == color)
return image;
// 方向
int[] di = new int[] { 0, 0, 1, -1 };
int[] dj = new int[] { 1, -1, 0, 0 };
// 队列
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[] { sr, sc });
int m = image.length, n = image[0].length;
while (!queue.isEmpty()) {
int[] arr = queue.poll();
int x = arr[0], y = arr[1];
image[x][y] = color;
for (int i = 0; i < 4; i++) {
int a = x + di[i];
int b = y + dj[i];
if (0 <= a && a < m && 0 <= b && b < n && image[a][b] == prev) {
queue.add(new int[] { a, b });
}
}
}
return image;
}
}
class Solution {
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
int oldColor = image[sr][sc];
if(oldColor == color) return image; // 不能没有
int m = image.length;
int n = image[0].length;
image[sr][sc] = color;
for(int i=0;i<4;i++){
int x = sr+dx[i];
int y = sc+dy[i];
if(0<=x&&x<m&&0<=y&&y<n&&image[x][y]==oldColor){
floodFill(image,x,y,color);
}
}
return image;
}
}
DFS vs BFS:
30、岛屿数量
class Solution {
public int numIslands(char[][] grid) {
// 加强版图像渲染
// 引入一个二维数组用于标记是否已经探索过,可以直接修改元素组,一般都还是建立一个标记数组
int m = grid.length;
int n = grid[0].length;
int[] dx = new int[] { 0, 0, 1, -1 };
int[] dy = new int[] { 1, -1, 0, 0 };
boolean[][] flag = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
flag[i][j] = false;
}
}
// 创建队列;
Queue<int[]> queue = new LinkedList<>();
int ret = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1' && flag[i][j] == false) {
queue.add(new int[] { i, j });
flag[i][j] = true;
while (!queue.isEmpty()) {
int[] temp = queue.poll();
int x = temp[0], y = temp[1];
for (int k = 0; k < 4; k++) {
int a = x + dx[k], b = y + dy[k];
if (0 <= a && a < m && 0 <= b && b < n && grid[a][b] == '1' && flag[a][b] == false) {
queue.add(new int[] { a, b });
flag[a][b] = true;
}
}
}
ret++;
}
}
}
return ret;
}
}
class Solution {
int m;
int n;
public int numIslands(char[][] grid) {
m = grid.length;
n = grid[0].length;
int ret=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]=='1'){
dfs(grid,i,j);
ret++;
}
}
}
return ret;
}
int[] dx = { 0, 0, 1, -1 };
int[] dy = { 1, -1, 0, 0 };
void dfs(char[][] grid, int x, int y) {
// 标记这个位置已经蔓延过来,防止折返
grid[x][y]='0';
for (int i = 0; i < 4; i++) {
int a = x + dx[i];
int b = y + dy[i];
// 蔓延条件:坐标合法,性质相同
if (0 <= a && a < m && 0 <= b && b < n && grid[a][b]=='1') {
dfs(grid,a,b);
}
}
}
}
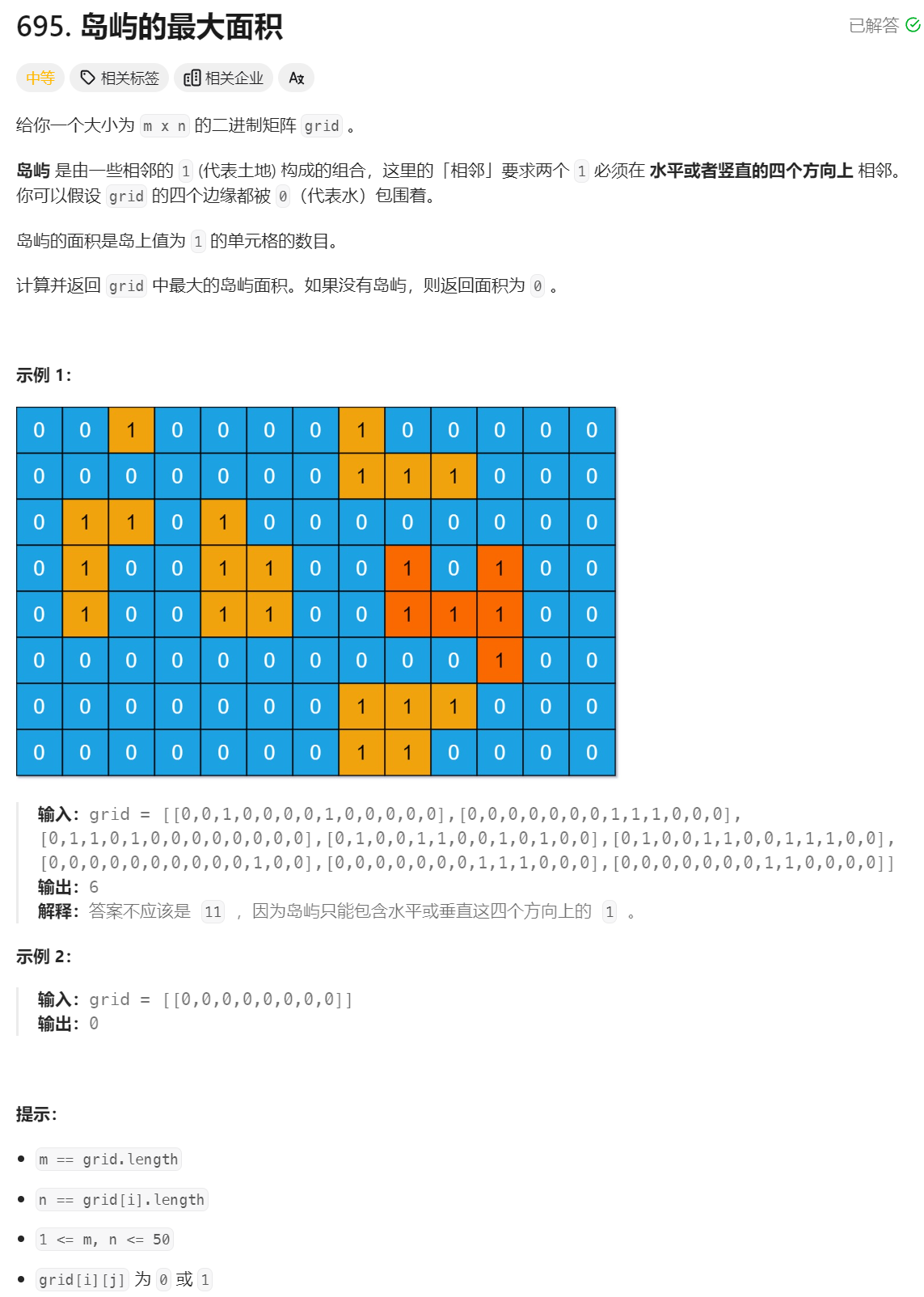
31、最大岛屿面积
class Solution {
public int maxAreaOfIsland(int[][] grid) {
// 加强版图像渲染
// 引入一个二维数组用于标记是否已经探索过,可以直接修改元素组,一般都还是建立一个标记数组
int m = grid.length;
int n = grid[0].length;
int[] dx = new int[] { 0, 0, 1, -1 };
int[] dy = new int[] { 1, -1, 0, 0 };
boolean[][] flag = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
flag[i][j] = false;
}
}
// 创建队列;
Queue<int[]> queue = new LinkedList<>();
int max = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1 && flag[i][j] == false) {
queue.add(new int[] { i, j });
flag[i][j] = true;
int size=0;
while (!queue.isEmpty()) {
int[] temp = queue.poll();
size++;
int x = temp[0], y = temp[1];
for (int k = 0; k < 4; k++) {
int a = x + dx[k], b = y + dy[k];
if (0 <= a && a < m && 0 <= b && b < n && grid[a][b] == 1 && flag[a][b] == false) {
queue.add(new int[] { a, b });
flag[a][b] = true;
}
}
}
max = Math.max(max,size);
}
}
}
return max;
}
}
class Solution {
int m;
int n;
int[] dx = { 0, 0, 1, -1 };
int[] dy = { 1, -1, 0, 0 };
public int maxAreaOfIsland(int[][] grid) {
m = grid.length;
n = grid[0].length;
int max = 0;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
if(grid[i][j]==1)
max = Math.max(max,dfs(grid,i,j));
return max;
}
int dfs(int[][] grid, int x, int y) {
// 记录岛屿大小
int ret = 1;
// 标记这个位置已经蔓延过了,防止折返
grid[x][y] = 0;
for (int i = 0; i < 4; i++) {
int a = x + dx[i];
int b = y + dy[i];
// 向四周继续蔓延的条件:坐标合法,性质相同
if (0 <= a && a < m && 0 <= b && b < n && grid[a][b] == 1) {
ret += dfs(grid, a, b);
}
}
return ret;
}
}
代码对DFS进行了修改,如果不想修改DFS可以添加一个布尔数组,比较遍历过的地方,防止重复遍历
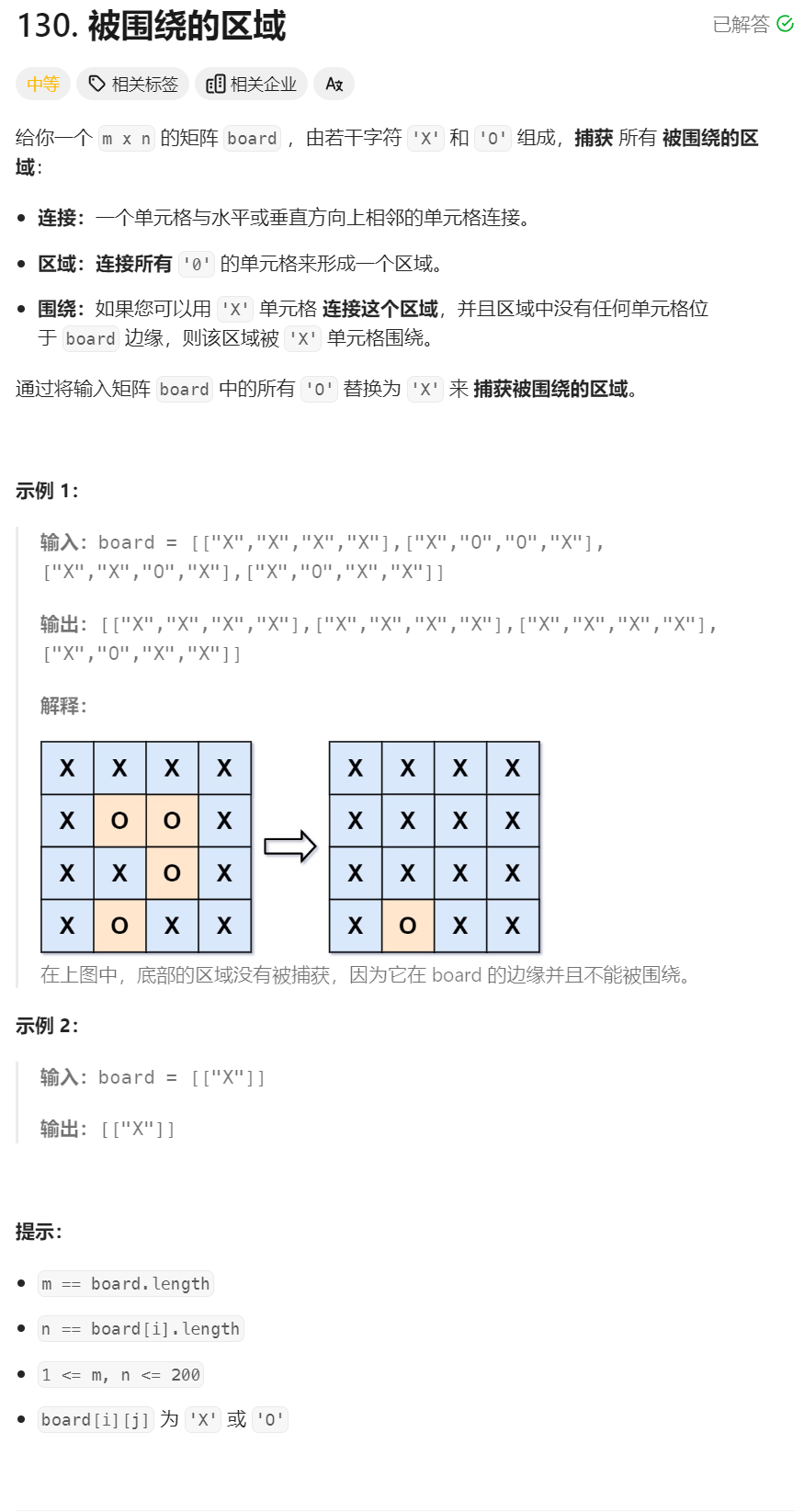
32、被围绕的区域
class Solution {
// 定义在里面的需要手动初始化
int[] dx = new int[] { 0, 0, 1, -1 };
int[] dy = new int[] { 1, -1, 0, 0 };
int m, n;
Queue<int[]> q = new LinkedList<>();
public void solve(char[][] board) {
m = board.length;
n = board[0].length;
// 1. 先处理边界的 'O' 联通块,全部修改成 '.'
for (int j = 0; j < n; j++) {
if (board[0][j] == 'O') {
bfs2(board, 0, j);
}
if (board[m - 1][j] == 'O') {
bfs2(board, m - 1, j);
}
}
// 1. 也是先处理边界的 'O' 联通块,全部修改成 '.'
for (int i = 0; i < m; i++) {
if (board[i][0] == 'O') {
bfs2(board, i, 0);
}
if (board[i][n - 1] == 'O') {
bfs2(board, i, n - 1);
}
}
// 构造返回值
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X';
}
if (board[i][j] == '.') {
board[i][j] = 'O';
}
}
}
}
public void bfs(char[][] board, int i, int j) {
q.add(new int[] { i, j });
while (!q.isEmpty()) {
int[] t = q.poll();
int a = t[0], b = t[1];
board[a][b] = '.';
for (int k = 0; k < 4; k++) {
int x = a + dx[k], y = b + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O') {
q.add(new int[] { x, y });
}
}
}
}
public void bfs2(char[][] board, int i, int j) {
board[i][j] = '.';
q.add(new int[] { i, j });
while (!q.isEmpty()) {
int[] temp = q.poll();
int x = temp[0], y = temp[1];
for (int k = 0; k < 4; k++) {
int a = x + dx[k], b = y + dy[k];
if (0 <= a && a < m && 0 <= b && b < n && board[a][b] == 'O') {
board[a][b] = '.';
q.add(new int[] { a, b });
}
}
}
}
}
class Solution {
// 定义在里面的需要手动初始化
int[] dx = new int[] { 0, 0, 1, -1 };
int[] dy = new int[] { 1, -1, 0, 0 };
int m, n;
Queue<int[]> q = new LinkedList<>();
public void solve(char[][] board) {
m = board.length;
n = board[0].length;
// 1. 先处理边界的 'O' 联通块,全部修改成 '.'
for (int j = 0; j < n; j++) {
if (board[0][j] == 'O') {
dfs(board, 0, j);
}
if (board[m - 1][j] == 'O') {
dfs(board, m - 1, j);
}
}
// 1. 也是先处理边界的 'O' 联通块,全部修改成 '.'
for (int i = 0; i < m; i++) {
if (board[i][0] == 'O') {
dfs(board, i, 0);
}
if (board[i][n - 1] == 'O') {
dfs(board, i, n - 1);
}
}
// 构造返回值
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X';
}
if (board[i][j] == '.') {
board[i][j] = 'O';
}
}
}
}
void dfs(char[][] board ,int x,int y){
board[x][y] = '.';
for (int i = 0; i < 4; i++) {
int a = x + dx[i];
int b = y + dy[i];
if (0 <= a && a < m && 0 <= b && b < n && board[a][b] == 'O') {
dfs(board, a, b);
}
}
}
}
只是讲BFS函数改为了DFS,solve函数的主体不变
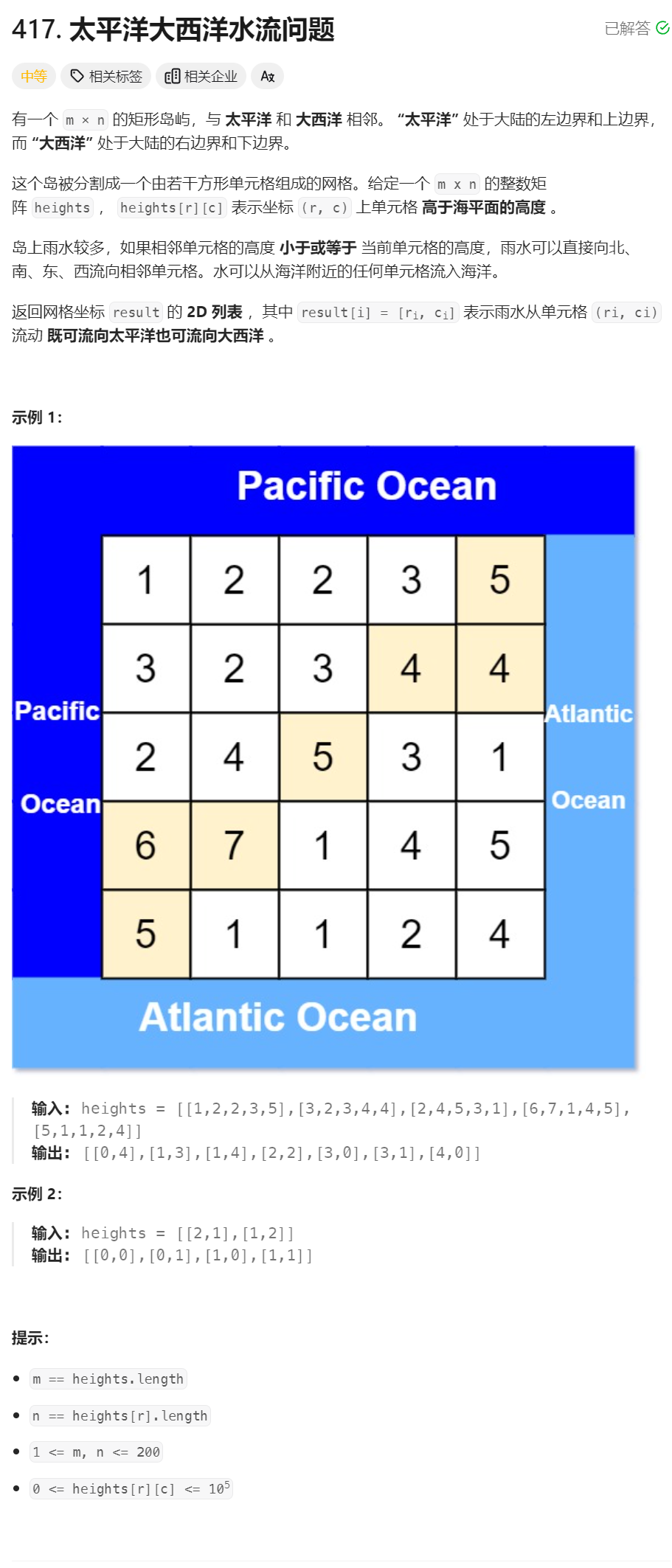
33、太平洋大西洋水流问题 (正南则反的典型案例)
class Solution {
int[] dx = new int[] { 0, 0, 1, -1 };
int[] dy = new int[] { 1, -1, 0, 0 };
int m, n;
boolean pacific;
boolean atlantic;
List<List<Integer>> ret;
boolean[][] cheak;
public List<List<Integer>> pacificAtlantic(int[][] heights) {
ret = new ArrayList<>();
m = heights.length;
n = heights[0].length;
cheak = new boolean[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
pacific = false;
atlantic = false;
dfs(heights,i,j);
if(pacific && atlantic){
List<Integer> arr = new ArrayList<>();
arr.add(i);
arr.add(j);
ret.add(arr);
}
}
}
return ret;
}
// 判断从某个位置开始是否可以流入大西洋和太平洋
void dfs(int[][] heights,int x,int y){
if(x==0||y==0) pacific = true;
if(x==m-1||y==n-1) atlantic = true;
if(pacific && atlantic) return;
for (int i = 0; i < 4; i++) {
int a = x + dx[i];
int b = y + dy[i];
if (0 <= a && a < m && 0 <= b && b < n && heights[x][y]>=heights[a][b] && !cheak[x][y]) {
cheak[x][y] = true;
dfs(heights, a, b);
cheak[x][y] = false;
}
}
}
}
思路一:设计dfs函数用于判断某一个点是否可以流入两个大洋,循环遍历每一个位置
class Solution {
int m, n;
int[] dx = { 0, 0, 1, -1 };
int[] dy = { 1, -1, 0, 0 };
public List<List<Integer>> pacificAtlantic(int[][] h) {
m = h.length;
n = h[0].length;
boolean[][] pac = new boolean[m][n];
boolean[][] atl = new boolean[m][n];
// 1. 先处理 pac 洋
for (int j = 0; j < n; j++)
dfs(h, 0, j, pac);
for (int i = 0; i < m; i++)
dfs(h, i, 0, pac);
// 2. 再处理 atl 洋
for (int i = 0; i < m; i++)
dfs(h, i, n - 1, atl);
for (int j = 0; j < n; j++)
dfs(h, m - 1, j, atl);
// 3. 提取结果
List<List<Integer>> ret = new ArrayList<>();
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (pac[i][j] && atl[i][j]) {
List<Integer> tmp = new ArrayList<>();
tmp.add(i);
tmp.add(j);
ret.add(tmp);
}
return ret;
}
public void dfs(int[][] h, int i, int j, boolean[][] vis) {
vis[i][j] = true;
for (int k = 0; k < 4; k++) {
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && h[x][y] >= h[i][j]) {
dfs(h, x, y, vis);
}
}
}
}
思路二:正难则反,从沿岸开始往上爬。分别从两个海岸往上爬,从两边都能爬到的地方就是答案。
34、扫雷问题
class Solution {
int[] dx = {0,0,1,-1,1,-1,1,-1};
int[] dy = {1,-1,0,0,1,-1,-1,1};
int m,n;
public char[][] updateBoard(char[][] board, int[] click) {
m = board.length;
n = board[0].length;
int x = click[0];
int y = click[1];
if(board[x][y]=='M'){
board[x][y]='X';
return board;
}else if(board[x][y]=='E'){
dfs(board,x,y);
return board;
}else{
return board;
}
}
void dfs(char[][] board,int x,int y){
int k = 0;
// 更具题目要求做事情:
for(int i=0;i<8;i++){
int a = x+dx[i];
int b = y+dy[i];
if(0<=a&&a<m&&0<=b&&b<n&&board[a][b]=='M') k++;
}
if(k>0){
board[x][y] = (char)('0'+k);
return ;
}
board[x][y] = 'B';
for(int i=0;i<8;i++){
int a = dx[i]+x;
int b = dy[i]+y;
if(0<=a&&a<m&&0<=b&&b<n&&board[a][b]=='E'){
dfs(board,a,b);
}
}
}
}
点击到炸弹就在updateBoard中解决,点击到空格在dfs中解决
35、衣柜整理
class Solution {
int m, n, cnt;
int ret;
boolean[][] cheak;
public int wardrobeFinishing(int _m, int _n, int _cnt) {
m = _m;
n = _n;
cheak = new boolean[m][n];
cnt = _cnt;
dfs(0, 0);
return ret;
}
int[] dx = { 0, 1 };
int[] dy = { 1, 0 };
void dfs(int x, int y) {
//
if (fun(x) + fun(y) <= cnt) {
ret++;
// 标记已经遍历的地方
cheak[x][y] = true;
for (int i = 0; i < 2; i++) {
int a = dx[i] + x;
int b = dy[i] + y;
// 继续搜索的条件:坐标合法,未被搜索过
if (0 <= a && a < m && 0 <= b && b < n && !cheak[a][b])
dfs(a, b);
}
}
}
int fun(int x) {
int count = 0;
while (x > 0) {
count += x % 10;
x /= 10;
}
return count;
}
}
/*
* 0123
* 1234
* 2345
* 345
* 45
* 5
* 6
* 7
*/
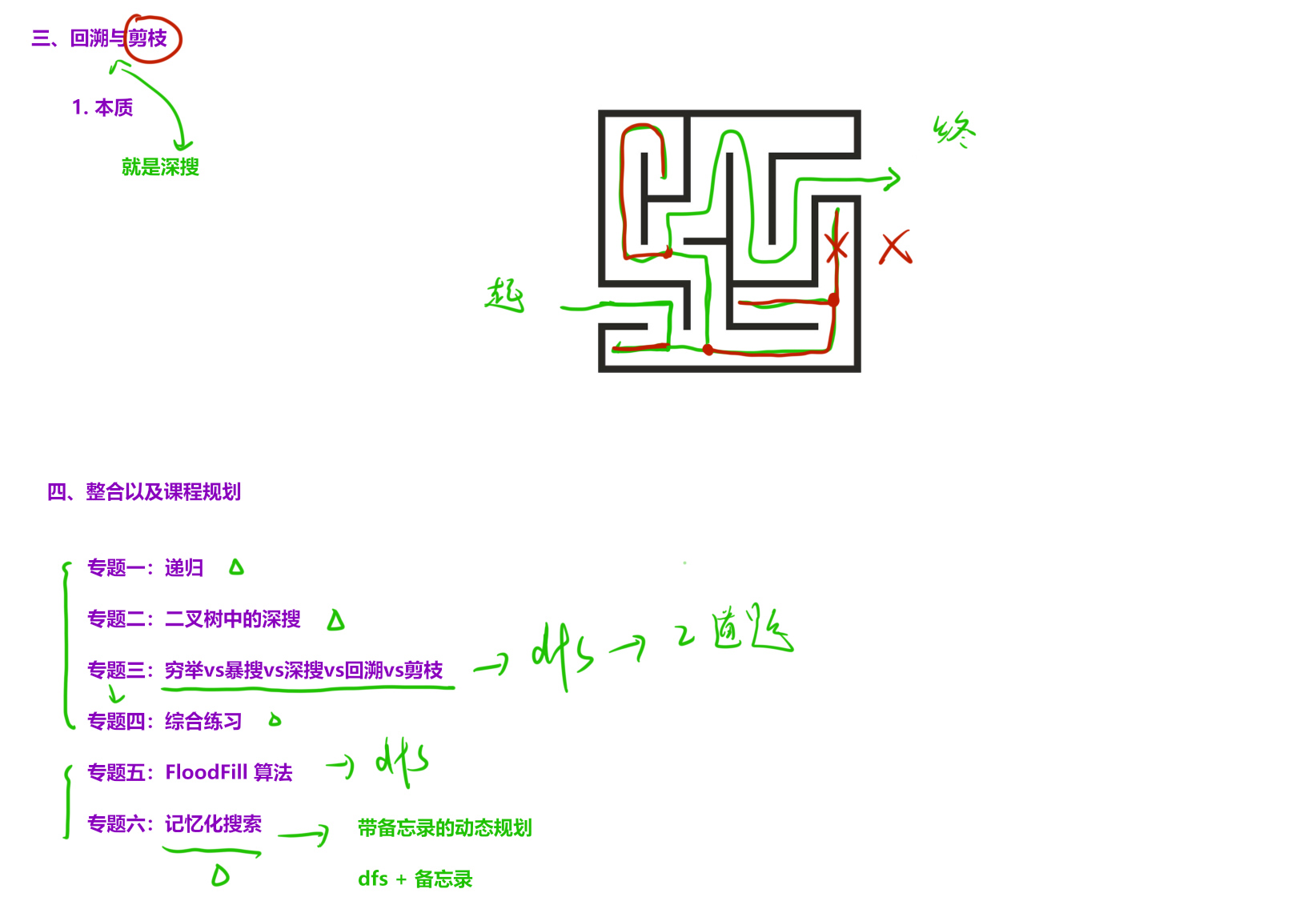
六、 记忆化搜索
36、斐波那契数
记忆化搜索与动态规划本质都是对暴搜的优化,只不过一个是递归形式,一个是循环形式
class Solution {
public int fib(int n) {
return dfs(n);
}
public int dfs(int n){
if(n==0) return 0;
if(n==1) return 1;
return dfs(n-1)+dfs(n-2);
}
}
class Solution {
int[] memo = new int[31];
public int fib(int n) {
// 初始化备忘录
for(int i=0;i<31;i++) memo[i]=-1;
return dfs(n);
}
int dfs(int n) {
if (memo[n] != -1){
return memo[n]; // 直接去备忘录⾥⾯拿值
}
if (n == 0 || n == 1) {
memo[n] = n; // 记录到备忘录⾥⾯
return n;
}
memo[n] = dfs(n - 1) + dfs(n - 2); // 记录到备忘录⾥⾯
return memo[n];
}
}
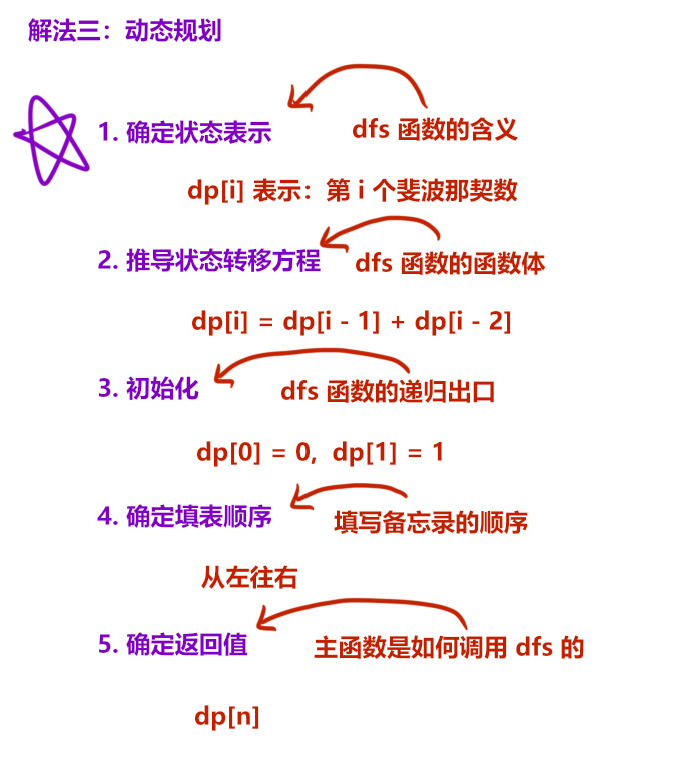
class Solution {
public int fib(int n) {
if(n<=1) return n;
int[] dp = new int[n+1];
dp[0]=0;
dp[1]=1;
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
}
记忆化搜索与动态规划本质都是对暴搜的优化,只不过一个是递归形式,一个是循环形式
37、不同路径
// 我的代码,自底向上
class Solution {
int[][] memo ;
int m,n;
public int uniquePaths(int _m, int _n) {
m = _m;
n = _n;
memo = new int[m+1][n+1];
return dfs(1,1);
}
int dfs(int x,int y){
if(x>m||y>n) return 0;
if(memo[x][y]!=0)
return memo[x][y];
//
if((x==m && y==n)||(x==m-1 && y==n)||(x==m && y==n-1)){
memo[x][y]=1;
return 1;
}
memo[x][y] = dfs(x+1,y)+dfs(x,y+1);// 这里忘记写了
return memo[x][y];
}
}
// 吴老师的代码,自顶向下
class Solution {
public int uniquePaths(int m, int n) {
// 记忆化搜索
int[][] memo = new int[m + 1][n + 1];
return dfs(m, n, memo);
}
public int dfs(int i, int j, int[][] memo) {
if (memo[i][j] != 0) {
return memo[i][j];
}
if (i == 0 || j == 0)
return 0;
if (i == 1 && j == 1) {
memo[i][j] = 1;
return 1;
}
memo[i][j] = dfs(i - 1, j, memo) + dfs(i, j - 1, memo);
return memo[i][j];
}
}
38、最长递增子序列
画决策树有助于写暴搜
class Solution {
public int lengthOfLIS(int[] nums) {
int max = 0;
// 循环求出以每一个位置为起点的最长递增子序列,然后取最大值
for(int i=0;i<nums.length;i++){
max = Math.max(max,dfs(nums,i));
}
return max;
}
// dfs:以index为起点的最长递增子序列
int dfs(int[] nums,int index){
int max = 0;
for(int i=index+1;i<nums.length;i++){
if(nums[i]>nums[index])
max = Math.max(max,dfs(nums,i));
}
return 1+max;
}
}
如何改成记忆化搜:
- 首先要确定重复子问题是什么
- 备忘录的初始化,如果备忘录中有结果直接从备忘录中返回即可
- 填写备忘录,将所有dfs的返回值都更新到备忘录中
- 有些是可以直接填写相当于递归出口或者是动态规划中dp表的初始化
- 有些是递归调用得出来的及结果
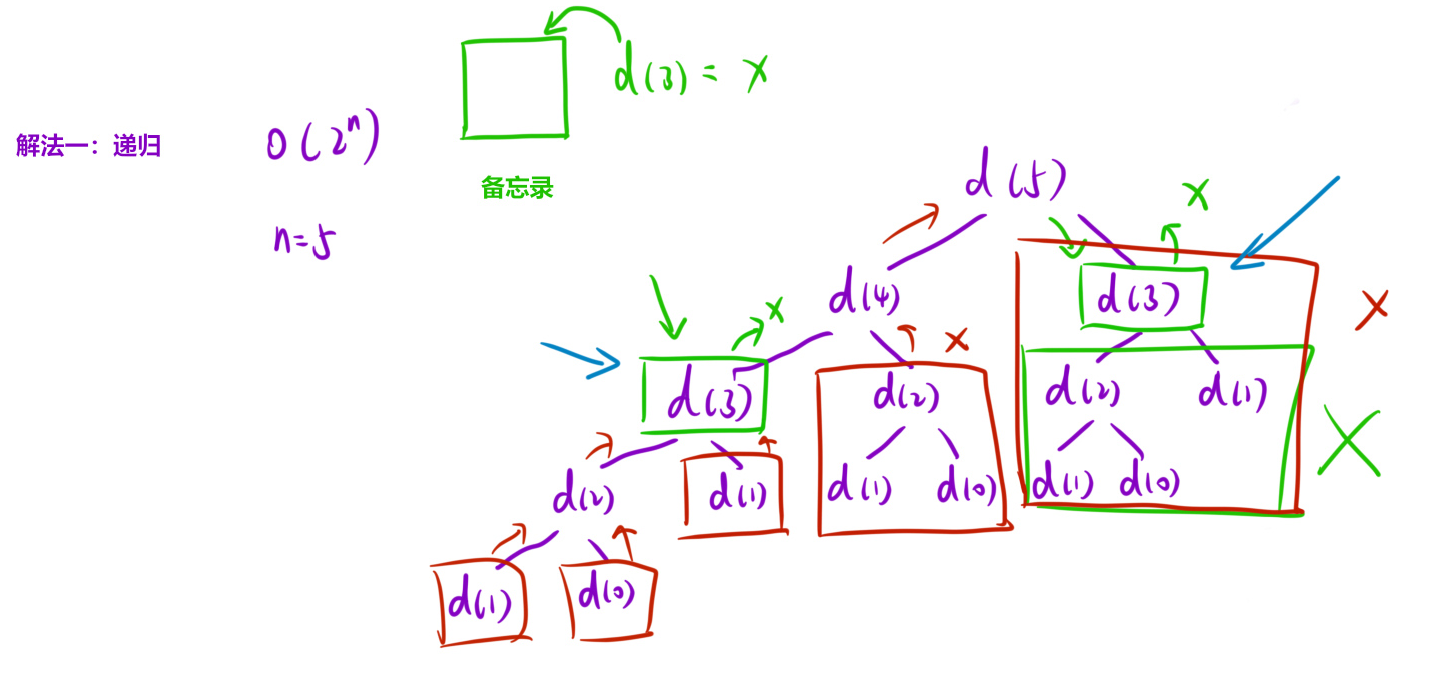
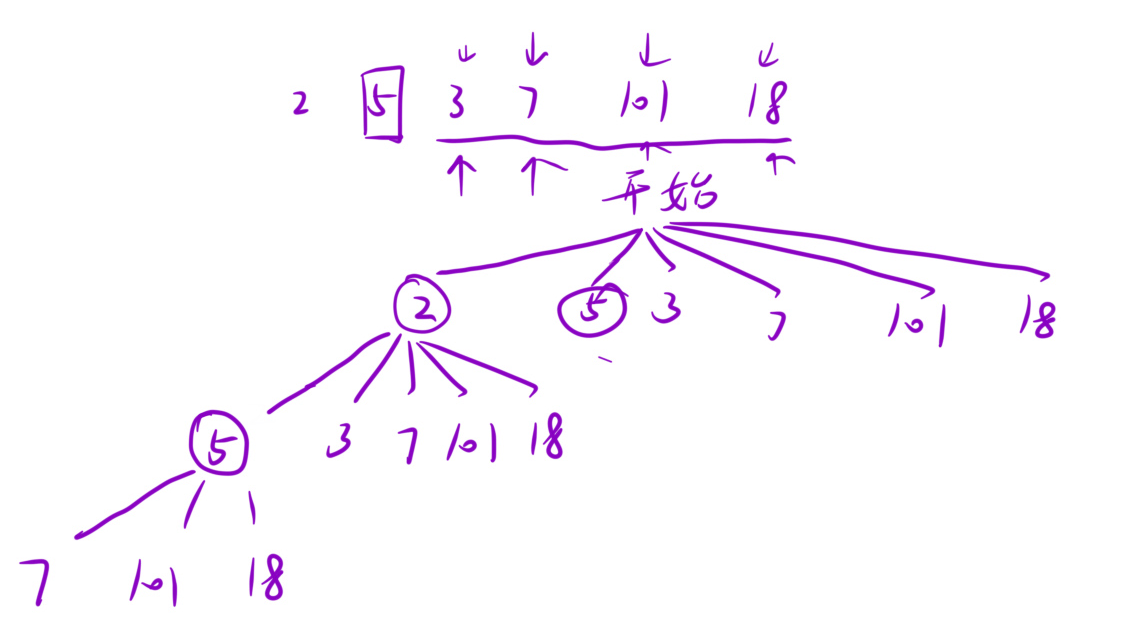
对于 nums={1,2,3,4,5},dfs(nums,1)和dfs(nums,2)都会调用dfs(nums,3),因此在计算dfs(nums,1)的时候会把dfs(nums,3)计算出来,将dfs(nums,3)的结果写入备忘录,当dfs(nums,2)掉用dfs(nums,3)时直接查找备忘录即可。
class Solution {
int[] memo;
public int lengthOfLIS(int[] nums) {
memo = new int[nums.length];
int max = 0;
for(int i=0;i<nums.length;i++){
max = Math.max(max,dfs(nums,i));
}
return max;
}
// dfs:以index为起点的最长递增子序列
int dfs(int[] nums,int index){
if(memo[index]!=0) return memo[index];
// 此处相当于递归出口,或者是动态规划中dp表的初始化
if(index==nums.length-1){
memo[index]=1;
return memo[index];
}
int max = 0;
for(int i=index+1;i<nums.length;i++){
if(nums[i]>nums[index]){
memo[i] = dfs(nums,i);
max = Math.max(max,memo[i]);
}
}
memo[index]=1+max;
return memo[index];
}
}
class Solution {
public int lengthOfLIS(int[] nums) {
int n = nums.length;
// dp[i]:以i位置为结尾的最长递增子序列的长度
int[] dp = new int[n];
dp[0] = 1;
int max =dp[0];
for(int i=1;i<n;i++){
dp[i] = 1;
for(int j=i-1;j>=0;j--){
if(nums[i]>nums[j]){
dp[i] = Math.max(dp[j]+1,dp[i]);
}
}
max = Math.max(max,dp[i]);
}
return max;
}
}
// 这一题的最优解是贪心策略
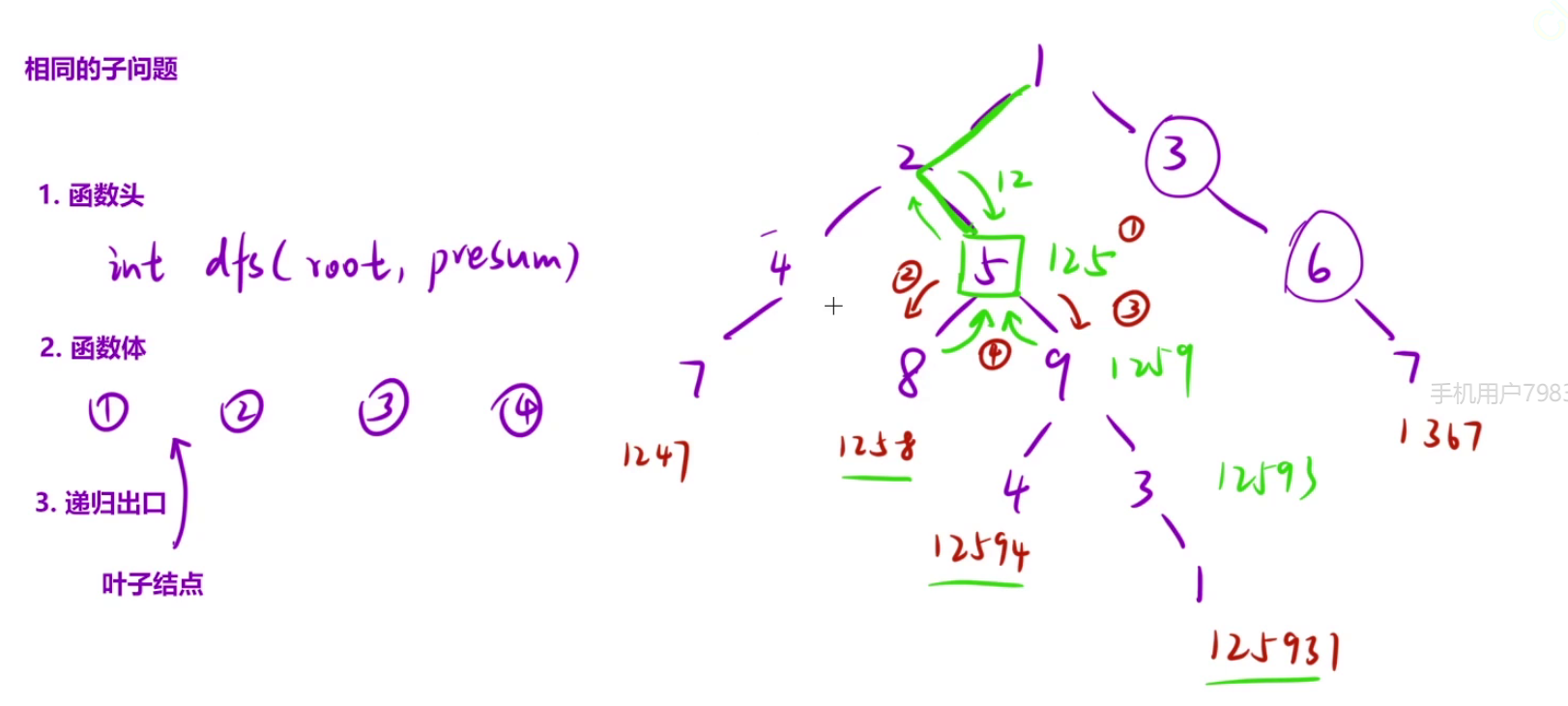
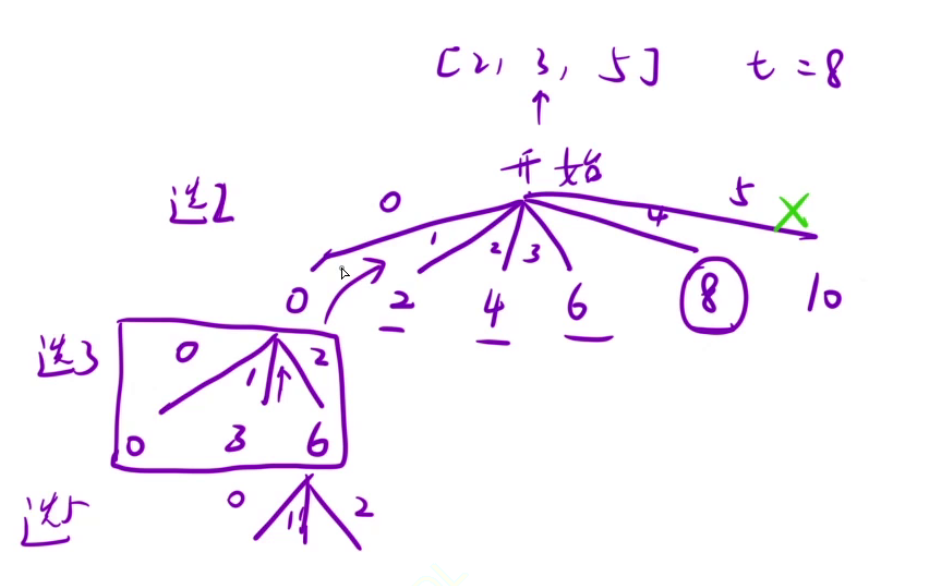
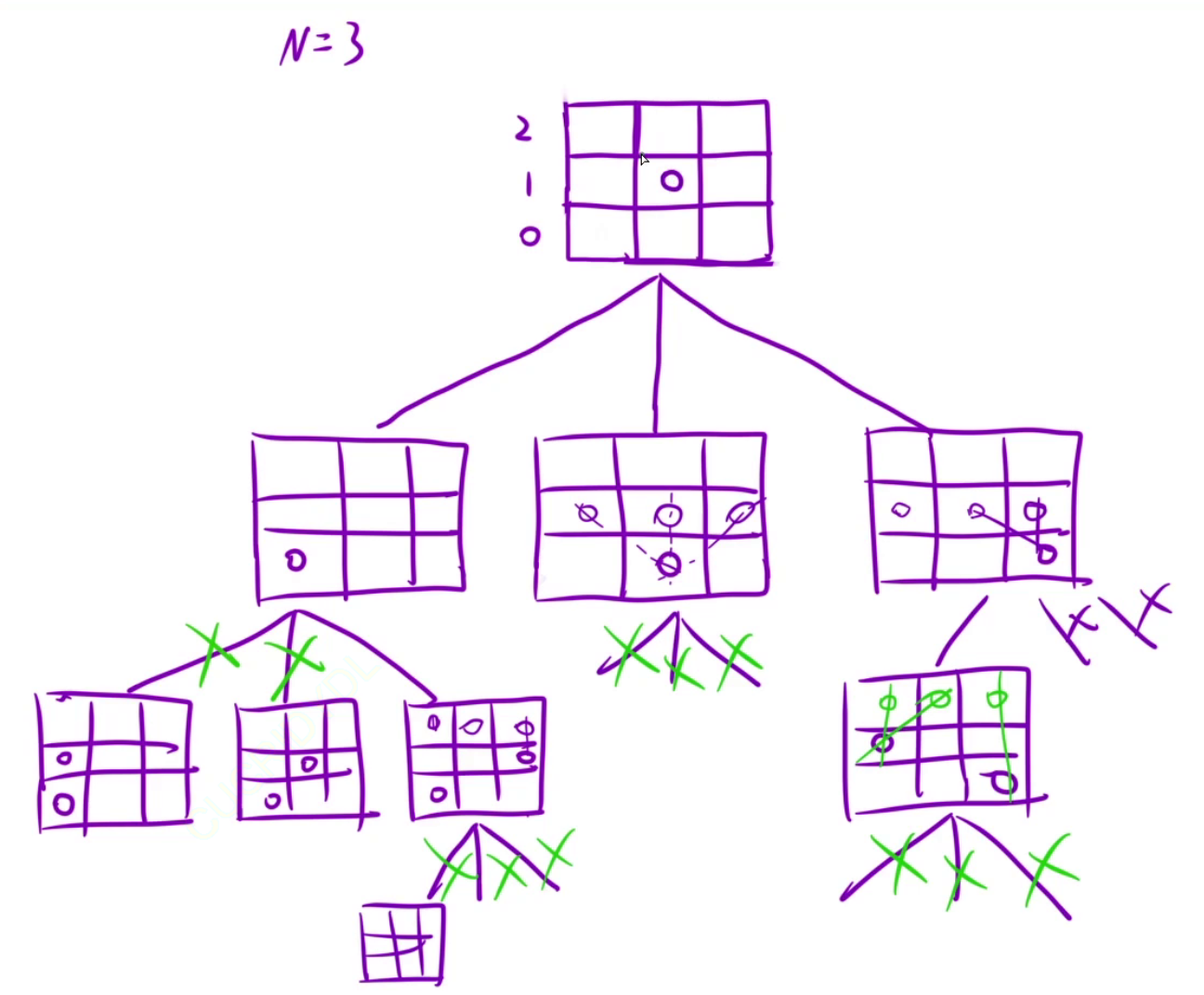
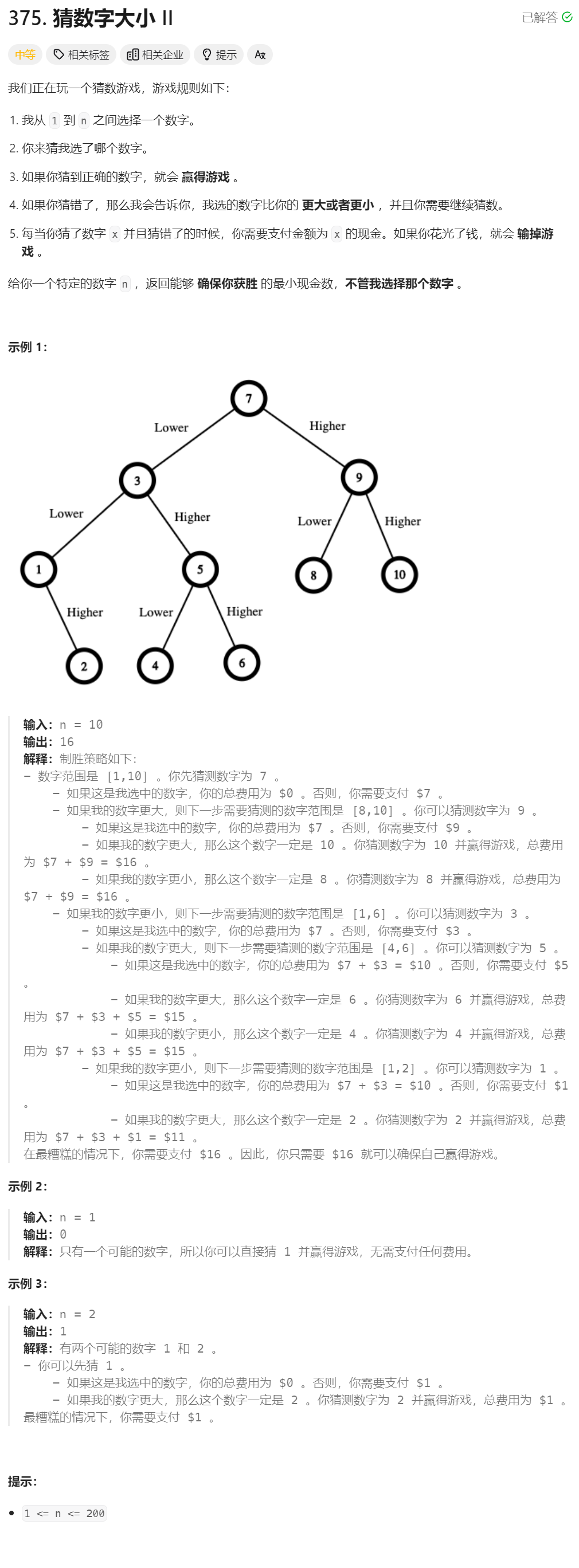
39、猜数字大小II ★★★★★(有趣,难)
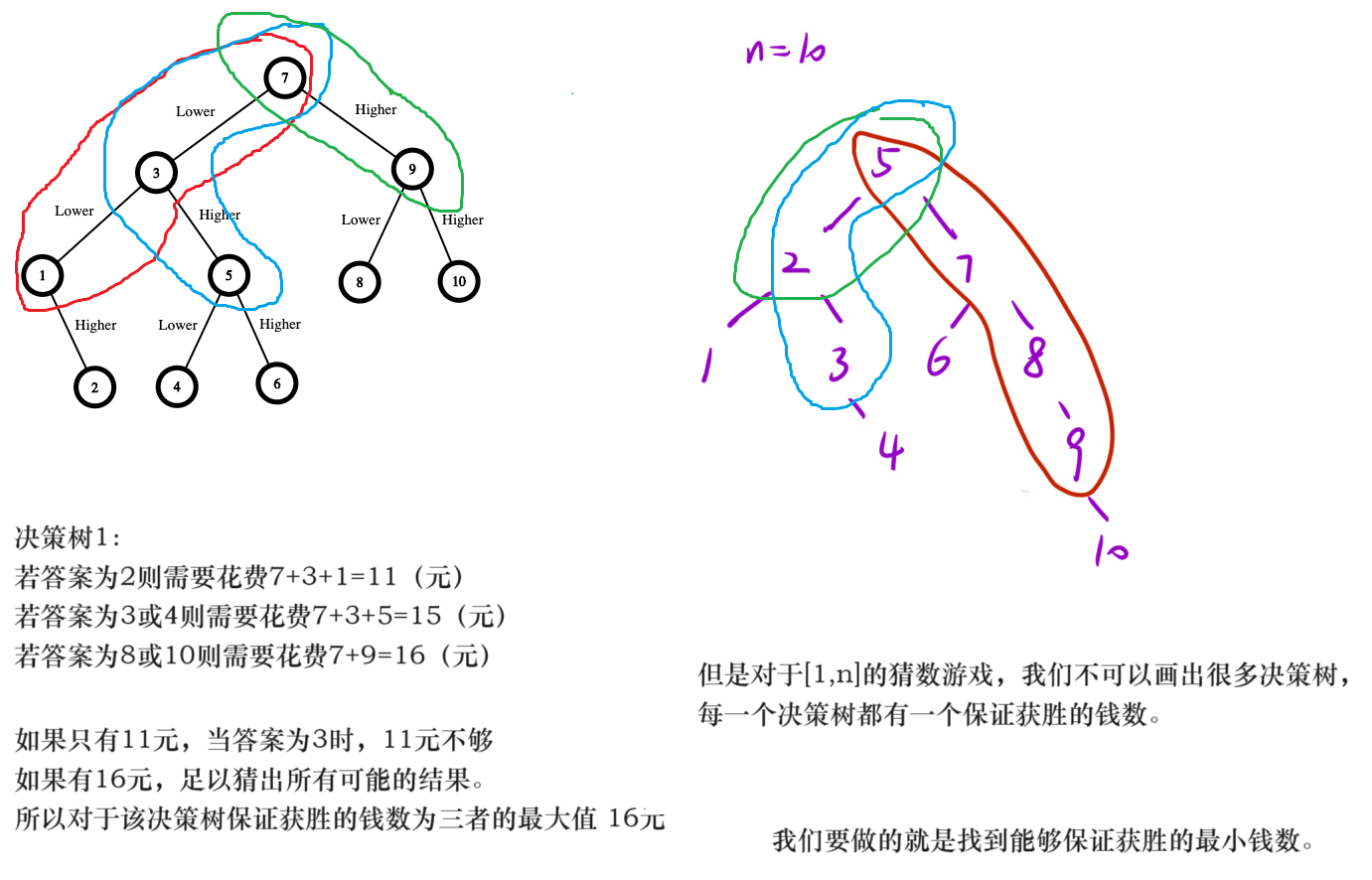
上图第二课决策树能保证获胜的钱数为5+7+8+9=29;
class Solution {
public int getMoneyAmount(int n) {
// 根据 dfs 的含义可知,dfs(1,n)就是题目的答案
return dfs(1,n);
}
// 保证游戏获胜的最小钱数游戏范围是[left,right];
int dfs(int left,int right){
// 两个特殊情况
if(left == right) return 0;
if(left+1==right) return left;
int ret = Integer.MAX_VALUE;
// 循环讨论,列举所有决策树
// 左子树:[left,i-1]
// 根节点: i
// 右子树:[i+1,right]
// 根据这个棵树保证能获胜的钱数为:根节点+左右子树的大者
for(int i = left+1;i<right;i++){
int temp = i + Math.max(dfs(left,i-1),dfs(i+1,right));
ret = Math.min(ret,temp);
}
return ret;
}
}
该问题存在重复子问题:dfs(a+b)和dfs(a,b-1)都会去调用dfs(a,i-1);
使用二维数组充当备忘录,memo[left,right]记录当猜数范围是[left,right]时的保证能获胜的最小金额
class Solution {
int[][] memo;
public int getMoneyAmount(int n) {
memo = new int[n+1][n+1];
return dfs(1,n);
}
int dfs(int left,int right){
if(memo[left][right]!=0) return memo[left][right];
if(left == right){
memo[left][right]=0;
return 0;
}
if(left+1==right) {
memo[left+1][right] = 0;
return left;
}
int ret = Integer.MAX_VALUE;
for(int i = left+1;i<right;i++){
// 注意这里要用max,(dfs(left,i-1),dfs(i+1,right))是左右子树所需的最小值,
// 根节点所需的最小值为i+Math.max(dfs(left,i-1),dfs(i+1,right))
memo[left][i-1] = dfs(left,i-1);
memo[i+1][right] = dfs(i+1,right);
int temp = i+Math.max(memo[left][i-1],memo[i+1][right]);
ret = Math.min(ret,temp);
}
memo[left][right]=ret;
return ret;
}
}
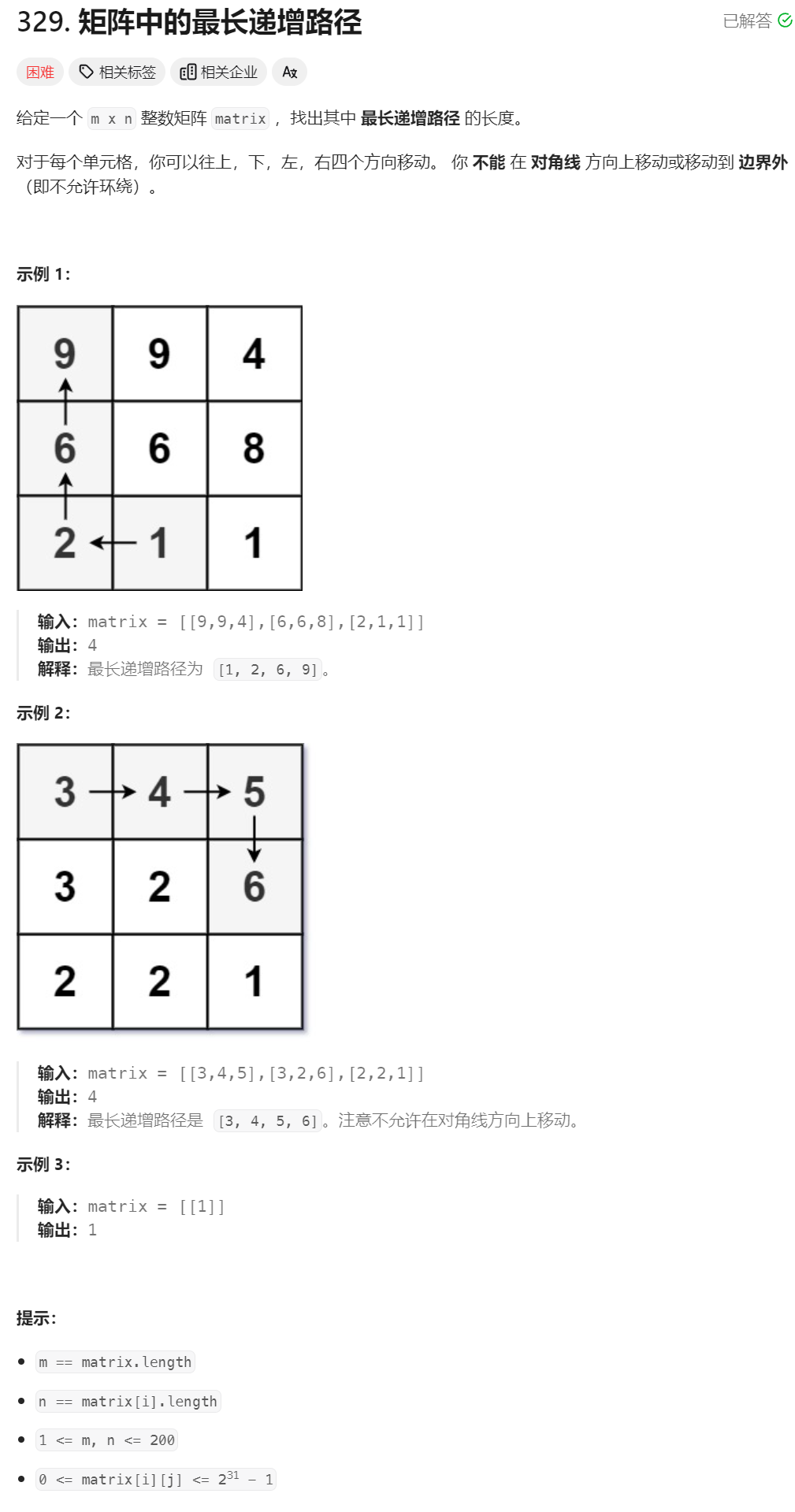
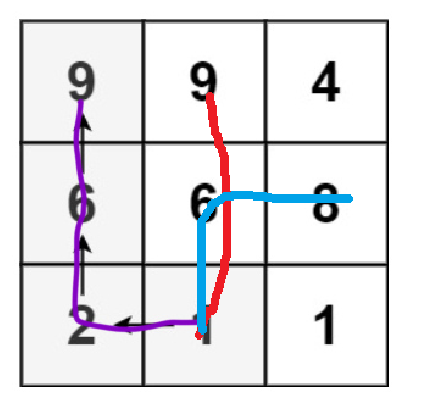
40、矩阵的最长递增路径
class Solution {
int m,n;
public int longestIncreasingPath(int[][] matrix) {
m = matrix.length;
n = matrix[0].length;
int max = 0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
// 循环计算以每一个位置为起点的最长递增路径,然后取最大值
max = Math.max(max,dfs(matrix,i,j));
}
}
return max;
}
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
// 求解的是以某一个位置为起点的最长递增路径
int dfs(int[][] matrix,int x,int y){
int max=0;
for(int i=0;i<4;i++){
int a = dx[i]+x;
int b = dy[i]+y;
if(0<=a&&a<m&&0<=b&&b<n&&matrix[a][b]>matrix[x][y]){
max = Math.max(max,dfs(matrix,a,b));
}
}
return 1+max;
}
}
从任意位置(x,y)开始沿着递增的方向深度优先搜索,记录路径的长度
class Solution {
int m,n;
int[][] memo;
public int longestIncreasingPath(int[][] matrix) {
m = matrix.length;
n = matrix[0].length;
memo = new int[m][n];
int max = 0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
max = Math.max(max,dfs(matrix,i,j));
}
}
return max;
}
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
// 题目存在重复子问题——>改成记忆化搜索的形式
// 使用二维数组充当备忘录,将dfs(a,b)存储在memo[a][b]中,
// 如果dfs[x][y]或者dfs[i][j]需要调用dfs(a,b)的时候直接查找memo即可
int dfs(int[][] matrix,int x,int y){
if(memo[x][y]!=0) return memo[x][y];
int max=0;
// 没有出口
for(int i=0;i<4;i++){
int a = dx[i]+x;
int b = dy[i]+y;
if(0<=a&&a<m&&0<=b&&b<n&&matrix[a][b]>matrix[x][y]){
memo[a][b] = dfs(matrix,a,b); // 将所有dfs()的结果补充到备忘录中
max = Math.max(max,memo[a][b]);
}
}
memo[x][y] = 1+max;// 将所有dfs()的结果补充到备忘录中
return 1+max;
}
}
dfs(matrix,x,y)从(x,y)位置开始像四个方向蔓延,然后取这四个方向递增路径的最大值,因为只是算出了以某位置为起点的最长递增路径长度,所以主函数要循环调用dfs来及计算以每一个位置为起点的最长递增路径,然后取最大值。