本文涉及知识点
LeetCode 3148. 矩阵中的最大得分
给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格(不必相邻)。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。
你可以从 任一 单元格开始,并且必须至少移动一次。
返回你能得到的 最大 总得分。
示例 1:
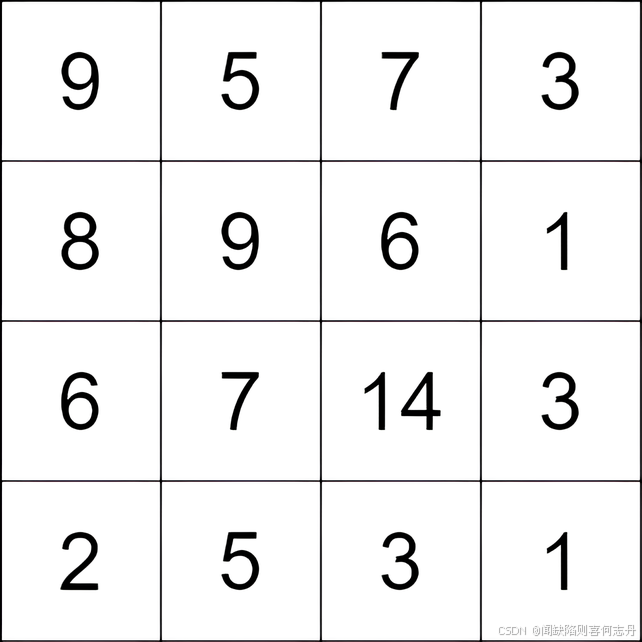
输入:grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]
输出:9
解释:从单元格 (0, 1) 开始,并执行以下移动:
- 从单元格 (0, 1) 移动到 (2, 1),得分为 7 - 5 = 2 。
- 从单元格 (2, 1) 移动到 (2, 2),得分为 14 - 7 = 7 。
总得分为 2 + 7 = 9 。
示例 2:
输入:grid = [[4,3,2],[3,2,1]]
输出:-1
解释:从单元格 (0, 0) 开始,执行一次移动:从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。
提示:
m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 105
1 <= grid[i][j] <= 105
动态规划
性质一:如果路径的节点超过或达到3个,只保留第一个节点和最后一个节点,得分不变。终点行列号都大于等于起点,但两者不能相等。
结论:无论是那种情况:都是枚举(r,c),求它的右边和下边的最大值iMax。所有 (iMax - grid[r][c])的最大值。
动态规划的状态表示
vMax[r][c]表示 grid[r…R-1][c…C-1]的最大值。 空间复杂度:O(mn)
为了方便处理边界,增加一行一列,值为INT_MAX/2。
动态规划的填表顺序
r = R-1 to 0 c = C-1 to 0
动态规划的转移方程
dp[r][c] = max(dp[r+1][c],dp[r][c+1])
ans = max(ans,dp[r][c]-grid[r][c])
dp[r][c] = max(dp[r][c],grid[r][c])
动态规划的初值
INT_MAX/2
动态规划的返回值
ans
代码
核心代码
class Solution {
public:
int maxScore(vector<vector<int>>& grid) {
const int R = grid.size(), C = grid[0].size();
vector<vector<int>> vMax(R + 1, vector<int>(C + 1, INT_MIN / 2));
int ans = INT_MIN / 2;
for (int r = R - 1; r >= 0; r--) {
for (int c = C - 1; c >= 0; c--) {
vMax[r][c] = max(vMax[r + 1][c], vMax[r][c + 1]);
ans = max(ans,vMax[r][c] - grid[r][c]);
vMax[r][c] = max(vMax[r][c], grid[r][c]);
}
}
return ans;
}
};
单元测试
vector<vector<int>> grid;
TEST_METHOD(TestMethod11)
{
grid = { {9,5,7,3},{8,9,6,1},{6,7,14,3},{2,5,3,1} };
auto res = Solution().maxScore(grid);
AssertEx(9, res);
}
TEST_METHOD(TestMethod12)
{
grid = { {4,3,2},{3,2,1} };
auto res = Solution().maxScore(grid);
AssertEx(-1, res);
}
扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。