摘要

https://arxiv.org/pdf/2407.04620
自注意力机制在长文本语境中表现良好，但其复杂度为二次方。现有的循环神经网络（RNN）层具有线性复杂度，但其在长文本语境中的性能受到隐藏状态表达能力的限制。我们提出了一种新的序列建模层类，该类具有线性复杂度和高表达能力的隐藏状态。核心思想是将隐藏状态本身视为一个机器学习模型，而其更新规则则是自监督学习的一个步骤。由于隐藏状态甚至在测试序列上通过训练进行更新，因此我们的层被称为测试时训练（Test-Time Training，TTT）层。我们考虑了两个实例化：TTT-Linear和TTT-MLP，其隐藏状态分别为线性模型和两层多层感知器（MLP）。我们在1.25亿至13亿参数的规模上评估了我们的实例化，并与强大的Transformer和现代RNN Mamba进行了比较。TTT-Linear和TTT-MLP均达到或超过了基线。与Transformer类似，它们可以通过对更多令牌的依赖来持续降低困惑度，而Mamba在16k语境之后则无法做到这一点。在进行了初步的系统优化后，TTT-Linear在8k语境下已经比Transformer更快，并且在实际运行时间方面与Mamba相当。TTT-MLP在内存I/O方面仍面临挑战，但在长文本语境中展现出更大的潜力，为未来的研究指明了一个有前途的方向。

1、引言

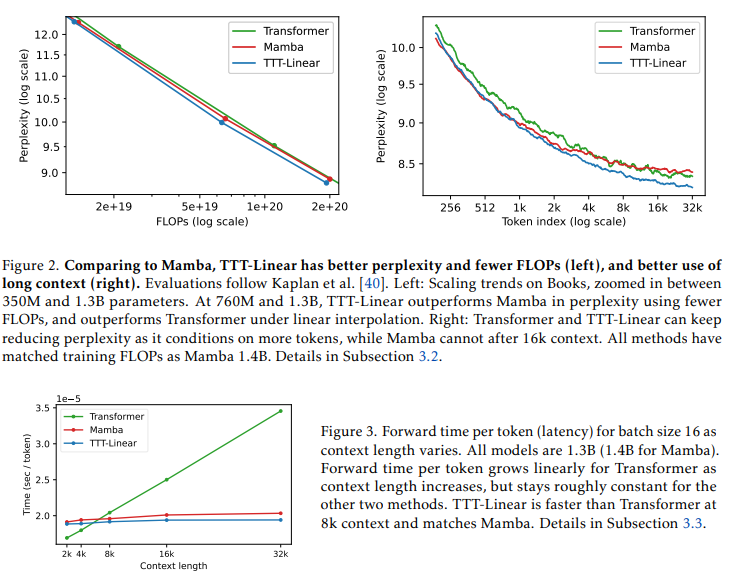
2020年，OpenAI的扩展定律论文（Kaplan等人[40]）表明，长短期记忆网络（LSTM，一种循环神经网络RNN）无法像Transformer那样进行扩展，也无法有效地利用长文本语境。现在，借助现代RNN和最佳实践，我们在图2中重新评估了这些发现。

在左侧，我们观察到，Mamba[26]——当今最流行的RNN之一——的扩展能力与强大的Transformer相似，自2020年的LSTM以来取得了巨大进步。然而，在右侧，我们观察到Mamba存在与Kaplan等人对LSTM描述相同的问题。序列中后面的令牌应该更容易预测，因为它们依赖于更多的信息。对于Transformer来说，确实如此，其每个令牌索引的平均困惑度在整个32k语境中都在下降。相比之下，Mamba在同一指标上在16k之后出现了停滞。

这一结果揭示了现有RNN的一个尴尬现实。一方面，RNN（与Transformer相比）的主要优势在于其线性（与二次方）复杂度。这种渐近优势只有在长文本语境中才能实现，根据图3，这通常发生在8k之后。另一方面，一旦语境足够长，现有的RNN（如Mamba）就难以实际利用所依赖的额外信息。

长文本语境的困难是RNN层的本质所固有的：与自注意力不同，RNN层必须将语境压缩成固定大小的隐藏状态。作为一种压缩启发式方法，更新规则需要发现成千上万个或可能数百万个令牌之间的潜在结构和关系。在本文中，我们首先观察到自监督学习可以将庞大的训练集压缩成模型（如大型语言模型LLM）的权重，这些模型通常对其训练数据之间的语义联系有深刻的理解——这正是我们需要的压缩启发式方法。

TTT层。基于这一观察，我们设计了一类新的序列建模层，其中隐藏状态是一个模型，而更新规则是自监督学习的一个步骤。由于在测试序列上更新隐藏状态的过程相当于在测试时训练一个模型，因此这一新类别的层被称为测试时训练（Test-Time Training，TTT）层。我们在这类层中引入了两个简单的实例化：TTT-Linear和TTT-MLP，其中隐藏状态分别是线性模型和两层多层感知器（MLP）。TTT层可以集成到任何网络架构中，并进行端到端的优化，类似于RNN层和自注意力机制。

实际运行时间。虽然TTT层在浮点运算次数（FLOPs）方面已经很高效，但我们提出了两项实用的创新来使其在实际运行时间上也变得高效。首先，类似于在常规训练期间在序列的小批量上执行梯度步骤的标准做法，以更好地实现并行性，我们在TTT期间也使用令牌的小批量。其次，我们为每个TTT小批量内的操作开发了一种对偶形式，以更好地利用现代GPU和TPU。对偶形式在输出上与原始实现等效，但训练速度提高了5倍以上。如图3所示，在8k语境下，TTT-Linear比Transformer更快，并且与Mamba相当。

评估与开放问题。虽然我们在论文开头已经强调了TTT-Linear的一些结果，但第3节对TTT-Linear和TTT-MLP进行了更全面的评估，并指出了评估中暴露出的开放问题。例如，我们按照Chinchilla的配方[34]进行的评估，即使对于Transformer基线，也不完全符合线性扩展趋势。受我们学术资源的限制，我们鼓励社区与我们一道探索这些问题的解决方案。

贡献总结：

1. 我们提出了TTT层，这是一种新的序列建模层类别，其中隐藏状态是一个模型，更新规则是自监督学习。我们认为层的正向传播本身就包含了一个训练循环，这为未来的研究开辟了一个新的方向。
2. TTT层的一个简单实例化——TTT-Linear，在我们从1.25亿到130亿参数的评估中，表现优于Transformer和Mamba。
3. 我们通过小批量TTT和对偶形式提高了TTT层的硬件效率，使得TTT-Linear已经成为大型语言模型（LLMs）的一个实用构建块。

2、方法

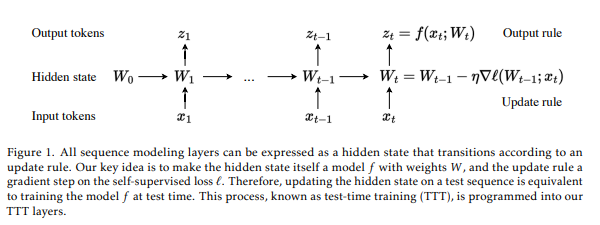
所有序列建模层都可以从将历史上下文存储到隐藏状态的角度来观察，如图4所示。{ }^{1} 例如，RNN层（如LSTM[33]、RWKV[56]和Mamba[26]层）将上下文压缩成跨时间的固定大小的状态。这种压缩有两个结果。一方面，将输入标记$x_t$映射到输出标记$z_t$是高效的，因为更新规则和输出规则对每个标记都采取恒定时间。另一方面，RNN层在长上下文中的性能受其隐藏状态$s_t$的表达能力的限制。

自注意力也可以从上述角度观察，只是其隐藏状态（通常称为键值（KV）缓存）是一个随$t$线性增长的列表。其更新规则只是将当前的KV元组追加到这个列表中，而输出规则则扫描所有直到$t$的元组以形成注意力矩阵。隐藏状态明确存储了所有历史上下文而不进行压缩，这使得自注意力在长上下文中比RNN层更具表达能力。然而，扫描这个线性增长的隐藏状态也导致每个标记的处理时间线性增长。

为了在长上下文中保持高效且富有表达力，我们需要一个更好的压缩启发式算法。具体来说，我们需要将成千上万甚至可能数百万个标记压缩成一个隐藏状态，该状态能够有效地捕获这些标记的底层结构和关系。这听起来可能是一项艰巨的任务，但实际上我们所有人都已经熟悉这样的启发式算法。

2.1、TTT作为隐藏状态的更新

参数学习的过程可以看作是将庞大的训练集压缩成模型的权重。具体来说，我们知道通过自监督训练得到的模型能够捕获其训练数据背后的底层结构和关系[48]——这正是我们从压缩启发式算法中所需要的。

大型语言模型（LLMs）本身就是很好的例子。通过自监督任务（如下一个标记预测）进行训练后，它们的权重可以被视为互联网上现有知识的一种压缩存储形式。通过查询LLMs，我们可以从其权重中提取知识。更重要的是，LLMs通常能够深入理解现有知识之间的语义联系，以表达新的推理片段[1]。

我们的核心思想是利用自监督学习将历史上下文$x_1,\dots ,x_t$压缩成一个隐藏状态$s_t$，具体做法是将上下文视为一个未标记的数据集，将状态视为一个模型。具体来说，隐藏状态$s_t$现在等同于模型$f$的权重$W_t$，其中$f$可以是一个线性模型、一个小型神经网络或任何其他类型的模型。输出规则很简单：

$z_t=f\left(x_t;W_t\right)$

直观上，输出标记$z_t$只是模型$f$使用更新后的权重$W_t$对$x_t$的预测。更新规则是在某个自监督损失$\ell$上进行梯度下降的一步：

$W_t=W_{t-1}-\eta \nabla \ell \left(W_{t-1};x_t\right)$

其中学习率为$\eta$。从压缩的角度来看，每个启发式算法都需要决定记住或忘记哪些输入。我们的$W$会记住那些产生大梯度的输入——直观上，这些输入会使$W$学到很多东西。

关于$\ell$的一个选择是重建$x_t$本身。为了使学习问题变得非平凡，我们首先将$x_t$处理成一个损坏的输入${\tilde{x}}_t$（详情见第2.3小节），然后进行优化：

$\ell \left(W;x_t\right)={\Vert f\left({\tilde{x}}_t;W\right)-x_t\Vert }^2$

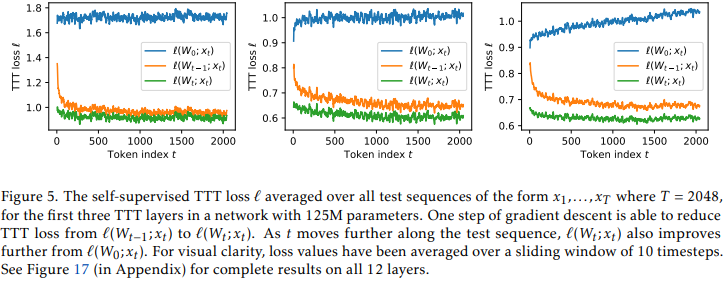
类似于去噪自编码器[75]，$f$需要发现$x_t$各维度之间的相关性，以便从部分信息${\tilde{x}}_t$中重建它。如图5所示，梯度下降能够减小$\ell$，但不能将其减小到零。我们在第2.3小节中讨论了自监督任务的更复杂表述。

与其他RNN层和自注意力机制一样，我们的算法将输入序列$x_1,\dots ,x_T$映射到输出序列$z_1,\dots ,z_T$，可以通过上述的隐藏状态、更新规则和输出规则，将其编写到序列建模层的前向传播中。即使在测试时，我们的新层仍然会为每个输入序列训练一个不同的权重序列$W_1,\dots ,W_T$。因此，我们称之为测试时训练（Test-Time Training，TTT）层。

2.2、使用TTT层的网络训练

TTT层的前向传播也有一个相应的反向传播。我们的前向传播只包含标准的可微运算符，除了梯度运算符$\nabla$。然而，$\nabla$只是将一个函数映射到另一个函数，在这个情况下是将$\ell$映射到$\nabla \ell$，而$\nabla \ell$也是由可微运算符组成的。从概念上讲，对$\nabla \ell$调用反向传播意味着对梯度求梯度——这是元学习中已经深入探索过的一种技术[51]。

TTT层与RNN层和自注意力机制具有相同的接口，因此可以在任何更大的网络架构中替换它们，这些网络架构通常包含许多这样的序列建模层。使用TTT层的网络训练方式与训练其他任何语言模型（如Transformer）的方式相同。可以使用相同的数据、配方和目标（如下一个标记预测）来优化网络其余部分的参数。

我们将训练整个较大的网络称为外层循环，将每个TTT层内的$W$训练称为内层循环。这两个嵌套的学习问题之间的一个重要区别在于，内层循环梯度$\nabla \ell$是相对于$f$的参数$W$的，而外层循环梯度是相对于网络其余部分的参数，我们用${\theta }_{\text{rest }}$来表示。在本文中，外层循环参数始终用带有不同下标的$\theta$来表示。

到目前为止，与其他RNN层和自注意力机制不同，TTT层没有外层循环参数。在第2.3小节中，我们为TTT层添加了外层循环参数，以改善其自监督任务。然后，在第2.4和2.5小节中，我们讨论了两种方法来改进TTT层的实际运行时间。

2.3、为TTT学习自监督任务

可以说，TTT中最重要的部分是自监督任务，因为它决定了$W$将从测试序列中学习哪种特征。那么我们应该如何设计这个任务呢？TTT的最终目标是使$z_t=f\left(x_t;W_t\right)$在语言建模上表现良好。我们不是根据人类先验知识来手工设计自监督任务，而是采用了一种更端到端的方法——直接针对最终目标（即下一个标记预测）来优化自监督任务。

具体来说，我们将自监督任务作为外层循环的一部分来学习。从方程3中的简单重建任务开始，我们添加了一些外层循环参数来使这个任务可学习。在第2.1小节中，我们没有指定从$x_t$生成${\tilde{x}}_t$的损坏方式。一种设计是使其成为低秩投影${\tilde{x}}_t={\theta }_K{x}_t$，其中${\theta }_K$是可学习矩阵。根据多视图重建的术语，${\theta }_K{x}_t$被称为训练视图[14]。

此外，可能不是$x_t$中的所有信息都值得记忆，因此重建标签可以是另一个低秩投影${\theta }_V{x}_t$，而不是$x_t$。这里，${\theta }_V{x}_t$被称为标签视图，其中${\theta }_V$也是可学习的。总之，我们新的自监督损失为：

$\ell \left(W;x_t\right)={\Vert f\left({\theta }_K{x}_t;W\right)-{\theta }_V{x}_t\Vert }^2$

由于$W$和各种$\theta$在方程4中同时出现，我们再次强调它们本质上的区别。在内层循环中，仅优化$W$，因此将其写为$\ell$的参数；而$\theta$是该损失函数的“超参数”。在外层循环中，${\theta }_K$、${\theta }_V$、${\theta }_Q$与${\theta }_{\text{rest }}$一起进行优化，而$W$仅是一个隐藏状态，不是参数。图6通过代码说明了这种区别，其中${\theta }_K$和${\theta }_V$被实现为TTT层的参数，类似于自注意力中的Key和Value参数。

最后，训练视图${\theta }_K{x}_t$的维度比$x_t$少，因此我们不能再使用方程1中的输出规则。最简单的解决方案是创建一个测试视图${\theta }_Q{x}_t$，并将我们的输出规则更改为：

$z_t=f\left({\theta }_Q{x}_t;W_t\right)$

这个解决方案还有一个额外的好处。训练和标签视图指定了$x_t$中压缩到$W_t$中并通过时间传播的信息。测试视图指定了可能不同的信息，这些信息被映射到当前输出标记$z_t$上并通过网络层传播，因此为自监督任务增加了更多的灵活性。

综上所述，${\theta }_K$、${\theta }_Q$、${\theta }_V$所有可能选择的集合引出了一个多视图重建任务的族，而外层循环可以被解释为从这个族中选择一个任务。为了简化，我们已将所有视图设计为线性投影。未来的工作可能会尝试更灵活的变换，或者更大、不同的自监督任务族。

2.4、使用小批量TTT的并行化

迄今为止开发的原始TTT层在浮点运算（FLOPs）数量上已经相当高效。然而，其更新规则$W_t=W_{t-1}-\eta \nabla l\left(W_{t-1};x_t\right)$无法并行化，因为$W_t$在两个地方依赖于$W_{t-1}$：在减号之前和在$\nabla l$内部。由于$\nabla l$包含了大部分计算，我们专注于使第二部分并行化。

我们通过TTT框架中的概念来解决这一系统挑战。梯度下降（GD）有许多变体。GD的一般更新规则可以表示为：

$W_t=W_{t-1}-\eta G_t=W_0-\eta {\sum }_{s=1}^t{G}_s$

其中$G_t$是下降方向。注意，一旦我们为$t=1,\dots ,T$计算了$G_t$，我们就可以通过方程6的第二部分进行累积求和来获得所有$W_t$。我们的朴素更新规则，即在线梯度下降，使用$G_t=\nabla l\left(W_{t-1};x_t\right)$。

为了并行化$G_t$（其中$t=1,\dots ,T$），我们可以将它们全部相对于$W_0$进行。这种使用$G_t=\nabla \ell \left(W_0;x_t\right)$的变体被称为批量梯度下降，因为${\sum }_{s=1}^t\nabla \ell \left(W_0;x_t\right)$与作为一批的$x_1,\dots ,x_t$相对于$W_0$的梯度相同。然而，在批量梯度下降中，$W_t$实际上仅距离$W_0$一个梯度步长，这与在线梯度下降形成对比，后者中$W_t$距离$W_0$有$t$个步长。因此，批量梯度下降的有效搜索空间较小，这最终会损害语言建模的性能。

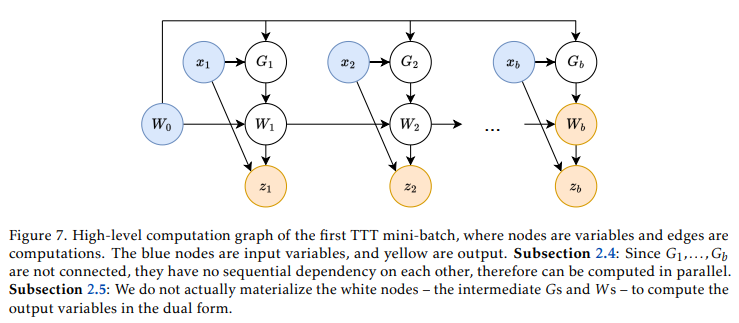
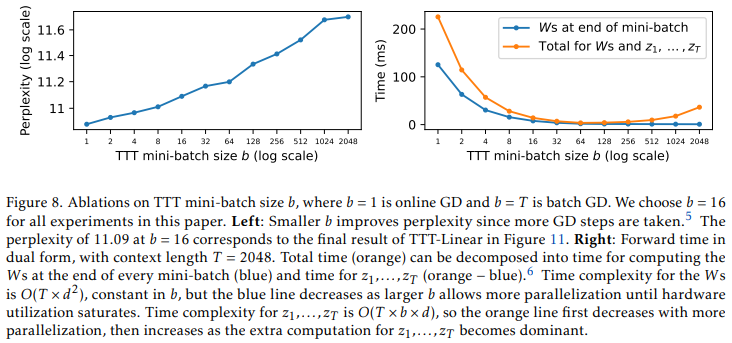
我们提出的解决方案——小批量梯度下降——如图7所示。设TTT的批量大小为$b$。我们使用$G_t=\nabla \ell \left(W_{t^{\prime }};x_t\right)$，其中$t^{\prime }=t-\mathrm{mod}(t,b)$是前一个小批量的最后一个时间步（对于第一个小批量，则为0），因此我们可以一次并行化$b$个梯度计算。根据经验，$b$控制着速度和质量之间的权衡，如图8所示。对于本文中的所有实验，我们选择$b=16$。

综上所述，存在两个潜在的通道来从$W_s$传播信息到$W_t$（其中$s<t$）：累积和和梯度算子。累积和始终处于活动状态，但梯度通道仅在$W_s$来自前一个小批量时处于活动状态。梯度下降的不同变体仅影响梯度通道，即下降方向$G_t$，特别是关于哪个$W$计算梯度。然而，由于更新规则的自回归性质，下降步$W_t=W_{t-1}-\eta G_t$始终从$W_{t-1}$开始，这与$G_t$的选择正交。

2.5 对偶形式

上面介绍的并行化对于减少实际运行时间来说是必要的，但还不够充分。现代加速器擅长矩阵-矩阵乘法（称为matmul）。例如，NVIDIA A100 GPU包含高度优化的单元，称为TensorCores，它们只能执行单一操作——即两个各为$16\times 16$大小的矩阵的乘法。如果没有足够的matmul操作，TensorCores将处于空闲状态，A100的大部分潜力将无法实现。

不幸的是，即使采用小批量方式，迄今为止开发的TTT层仍然包含非常少的matmul操作。考虑$\ell$的最简单情况，其中${\theta }_K={\theta }_V={\theta }_Q=I$，仅针对第一个大小为$b$的TTT小批量。此外，假设$f$是一个线性模型。复制方程3，我们在时间$t$的损失为：

$\ell \left(W_0;x_t\right)={\Vert f\left(x_t;W_0\right)-x_t\Vert }^2={\Vert W_0{x}_t-x_t\Vert }^2$

如小节2.4所述，我们可以并行化以下计算：

$G_t=\nabla \ell \left(W_0;x_t\right)=2\left(W_0{x}_t-x_t\right)x_t^T$

对于$t=1,\dots ,b$。但是，我们无法通过一个matmul来计算所有$b$个$G_t$。相反，我们需要$b$个外积来逐一计算它们。更糟糕的是，对于每个$x_t\in {\mathbb{R}}^d$，$G_t$是$d\times d$的，这导致对于较大的$d$，与$x_t$相比，其内存占用和I/O成本要大得多。

为了解决这两个问题，我们做了一个简单的观察：我们实际上不需要具体化$G_1,\dots ,G_b$，只要我们能在小批量结束时计算出$W_b$和输出标记$z_1,\dots ,z_b$（见图7）。现在，我们使用上面简化的TTT-Linear案例来演示这些计算。设$X=\left[x_1,\dots ,x_b\right]$，则：

$W_b=W_0-\eta {\sum }_{t=1}^b{G}_t=W_0-2\eta {\sum }_{t=1}^b\left(W_0{x}_t-x_t\right)x_t^T=W_0-2\eta \left(W_{0}X-X\right)X^T$

因此，$W_b$可以方便地通过matmul计算得到。为了计算$Z=\left[z_1,\dots ,z_b\right]$，我们知道：

$z_t=f\left(x_t;W_t\right)=W_t{x}_t=\left(W_0-\eta {\sum }_{s=1}^t{G}_s\right)x_t=W_0{x}_t-2\eta {\sum }_{s=1}^t\left(W_0{x}_s-x_s\right)x_s^T{x}_s$

设${\delta }_t={\sum }_{s=1}^t\left(W_0{x}_s-x_s\right)x_s^T{x}_s$和矩阵$\Delta =\left[{\delta }_1,\dots ,{\delta }_b\right]$。我们可以推导出：

$\Delta =\mathrm{mask}\left(X^{T}X\right)\left(W_{0}X-X\right)$

其中，mask是下三角掩码，元素全为0（类似于注意力掩码，但用0代替无穷大），并且$W_{0}X-X$可以从$W_b$的计算中重用。现在，$\Delta$也可以通过matmul方便地计算得到。将$\Delta$代回方程7，我们得到$Z=W_{0}X-2\eta \Delta$。

我们称这个过程为对偶形式，以区别于本小节之前的原始形式，其中$G$和$W$被显式地具体化。如前所述，这两种形式在输出上是等价的。原始和对偶的术语遵循了先前在TTT之外探索类似数学公式的工作[36,8,59]。在附录A中，我们展示了当$f$是具有非线性层的神经网络时，对偶形式仍然有效，只是符号更复杂。

在TTT小批量内，原始形式的时间复杂度为$O\left(b\times d^2\right)$。对偶形式单独计算$W_b$的时间复杂度也是$O\left(b\times d^2\right)$，但额外需要$O\left(b^2\times d\right)$的时间来计算$z_1,\dots ,z_b$。与原始形式相比，对偶形式牺牲了理论上的复杂度以换取硬件利用率。在实践中，$d$通常是几百，而$b$通常选择为16。因此，如图8右面板所示，计算$z_1,\dots ,z_b$的实际时间相对较短。在我们的JAX实现中，使用对偶形式的训练速度比使用原始形式快5倍以上。

2.6、理论等价性

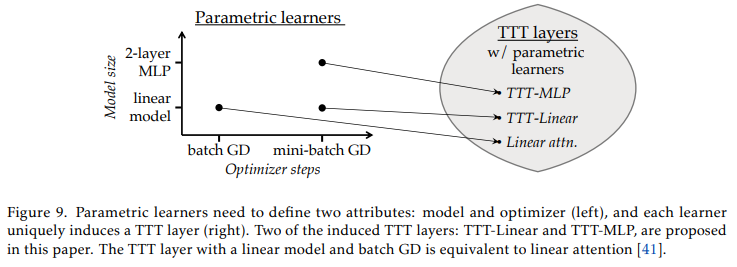
在2.1小节中，我们提到$f$可以是线性模型或神经网络。在2.4小节中，我们还讨论了更新规则的三种变体：在线梯度下降（GD）、批量梯度下降（GD）和小批量梯度下降（GD）。这些$2\times 3$组合中的每一种都会诱导出TTT层的一个不同实例化，如图9所示。我们现在表明，在这些诱导出的实例化中，使用线性模型和批量梯度下降的TTT层与线性注意力[41]（一种广为人知的RNN层）是等价的。{ }^7

定理1。考虑TTT层，其中$f(x)=Wx$作为内循环模型，批量梯度下降以$\eta =1/2$作为更新规则，且$W_0=0$。那么，对于相同的输入序列$x_1,\dots ,x_T$，方程5中定义的输出规则将产生与线性注意力相同的输出序列$z_1,\dots ,z_T$。

证明。根据方程4中$\ell$的定义，$\nabla \ell \left(W_0;x_t\right)=-2\left({\theta }_V{x}_t\right){\left({\theta }_K{x}_t\right)}^T$。根据方程6中批量梯度下降的定义：

$W_t=W_{t-1}-\eta \nabla \ell \left(W_0;x_t\right)=W_0-\eta {\sum }_{s=1}^t\nabla \ell \left(W_0;x_s\right)={\sum }_{s=1}^t\left({\theta }_V{x}_s\right){\left({\theta }_K{x}_s\right)}^T$

将$W_t$代入方程5中的输出规则，我们得到输出标记：

$z_t=f\left({\theta }_Q{x}_t;W_t\right)={\sum }_{s=1}^t\left({\theta }_V{x}_s\right){\left({\theta }_K{x}_s\right)}^T\left({\theta }_Q{x}_t\right)$

这正是线性注意力的定义。

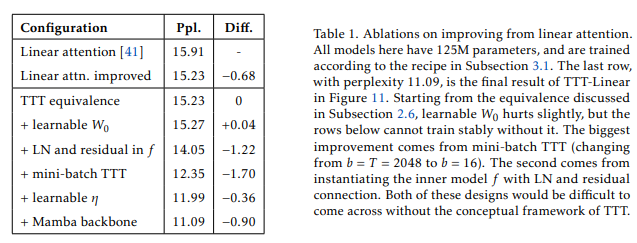
在表1中，我们首先通过改进线性注意力的实现来经验性地验证上述等价性。{ }^8 然后，为了说明我们每个组件（包括将在下一小节中介绍的一些组件）的贡献，我们将它们逐行添加到与线性注意力等价的TTT层中，并最终得到我们提出的实例化，称为TTT-Linear。从批量梯度下降（GD）到小批量梯度下降（GD）的变更带来了极大的改进。

尽管图9中模型$\times$优化器的空间已经很大，但机器学习远比优化模型$f$的参数$W_t$要丰富得多。还有非参数学习器，如最近邻、支持向量机（SVM）和核岭回归。根据定义，非参数学习器没有参数$W_t$，而是直接使用训练数据$x_1,\dots ,x_t$。因此，我们使用符号$f\left(x;x_1,\dots ,x_t\right)$。我们现在证明，对于特定的非参数学习器，诱导出的TTT层与自注意力是等价的。
定理2. 考虑使用Nadaraya-Watson估计器[7, 12]定义的TTT层，定义为：

$f\left(x;x_1,\dots ,x_t\right)=\frac{1}{{\sum }_{s=1}^t\kappa \left(x,x_s\right)}{\sum }_{s=1}^t\kappa \left(x,x_s\right)y_s,$

其中$y_s={\theta }_V{x}_s$是2.3小节中讨论的标签视图，并且

$\kappa \left(x,x^{\prime };{\theta }_K,{\theta }_Q\right)\propto e^{{\left({\theta }_{K}x\right)}^T{\theta }_Q{x}^{\prime }}$

是一个具有带宽超参数${\theta }_K$和${\theta }_Q$的核函数。那么，给定相同的输入序列$x_1,\dots ,x_T$，方程5中定义的输出规则将产生与自注意力相同的输出序列$z_1,\dots ,z_T$。

证明. 将上述的$y_s$和$\kappa$代入方程8，我们得到自注意力的定义。
附录B详细解释了上述的Nadaraya-Watson估计器和核函数$\kappa$。与定理1不同，定理2并没有产生与注意力不同的实现。
对于上述的TTT层，隐藏状态是$x_1,\dots ,x_t$或类似的已处理训练数据列表，更新规则将$x_t$添加到列表中，而输出规则则使用$\kappa$扫描该列表。在前面的子节中，我们的隐藏状态被定义为$W_t$，更新规则是一个梯度步骤，而输出规则是对$f$的调用。为了统一这两种构造，我们定义了一个新的抽象，称为学习器，它唯一地诱导出一个TTT层。
类似于标准机器学习包[54]中的定义，所有学习器都需要实现两个方法：训练和预测。现在，我们重新定义了诱导TTT层的隐藏状态作为学习器的内部存储，以及将更新和输出规则作为训练和预测方法。

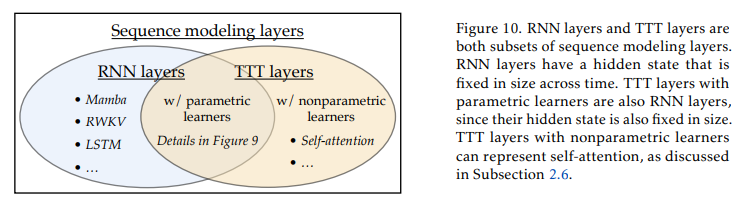
在新的TTT层定义下，无论是定理1中的参数学习器还是定理2中的非参数学习器都可以被包含在内。图10总结了在所有序列建模层更广泛范围内TTT层的一般定义。

这个一般定义对参数学习器还有一个额外的好处：在参数学习器的内部存储中，除了$W$之外还可以有其他更多的对象，比如优化器状态，这些也将被包含在诱导TTT层的隐藏状态中。这一扩展允许TTT层在未来的工作中使用更复杂的优化器，如Adam[42]。

2.7 实现细节

$f$的实例化。我们提出了TTT层的两种变体——TTT-Linear和TTT-MLP，它们仅在$f$的实例化上有所不同。对于TTT-Linear，$f_{\text{lin }}(x)=Wx$，其中$W$是方阵。对于TTT-MLP，$f_{\text{MLP }}$具有与Transformer中的MLP相似的两层结构。具体来说，隐藏维度是输入维度的$4\times$，之后是GELU激活函数[31]。为了在TTT过程中获得更好的稳定性，$f$总是包含一个层归一化（LN）和残差连接。即，$f(x)=x+\mathrm{LN}\left(f_{\text{res }}(x)\right)$，其中$f_{\text{res }}$可以是$f_{\text{lin }}$或$f_{\text{MLP }}$。

可学习权重$W_0$。尽管后续权重$W_1,\dots ,W_T$对于每个输入序列来说都是不同的，但TTT初始化权重$W_0$在所有序列之间是共享的。我们不将$W_0$设置为0，而是将其作为外部循环的一部分进行学习。由于外部循环参数通常用$\theta$s表示而不是$W$s，我们为$W_0$分配一个别名${\theta }_{\text{init }}$。在实际应用中，与重建视图${\theta }_K,{\theta }_Q,{\theta }_V$相比，${\theta }_{\text{init }}$增加的参数量可忽略不计，因为其输入和输出都是低维的。根据经验，我们观察到学习$W_0$可以显著提高训练的稳定性。

可学习学习率$\eta$。学习率通常是梯度下降中最重要的超参数，因此我们尝试将方程6中的内部循环学习率$\eta$作为外部循环的一部分进行学习。为了使$\eta$更加灵活，我们将其设计为输入标记的函数（因此随时间变化）。具体来说，我们设计$\eta (x)={\eta }_{\text{base }}\sigma \left({\theta }_{\mathrm{lr}}\cdot x\right)$，其中可学习向量${\theta }_{\mathrm{lr}}$是外部循环参数，$\sigma$是sigmoid函数，标量${\eta }_{\text{base }}$是基础学习率，对于TTT-Linear设置为1，对于TTT-MLP设置为0.1。另外，$\eta (x)$也可以被解释为$\nabla \ell$的门控。

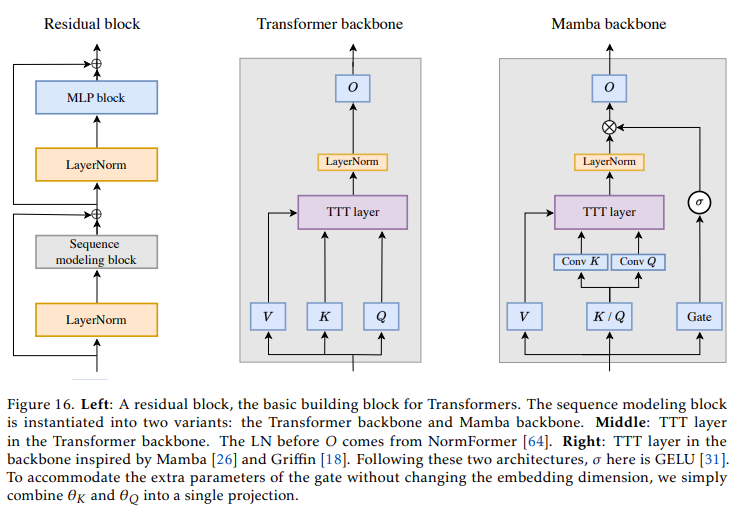
骨干架构。将任何RNN层集成到更大架构中最简洁的方式是直接替换Transformer中的自注意力机制，这在此上下文中被称为骨干。然而，现有的RNN，如Mamba[26]和Griffin[18]，都使用了与Transformer不同的骨干架构。最值得注意的是，它们的骨干在RNN层之前包含了时间卷积，这可能有助于跨时间收集局部信息。在尝试了Mamba骨干之后，我们发现它也能改善TTT层的困惑度，因此我们将其纳入了我们提出的方法中。有关详细信息，请参阅附录中的图16。

3、实验

我们通过将TTT-Linear和TTT-MLP与两个基线模型——Transformer和现代RNN Mamba进行比较来评估它们的性能。我们的主要代码库基于EasyLM[25]，这是一个用于在JAX中训练和部署大型语言模型（LLMs）的开源项目。所有实验都可以使用第一页底部提供的公开代码和数据集进行复现。

数据集。遵循Mamba论文[26]中的方法，我们在Pile[24]数据集上进行了标准实验，该数据集是训练开源LLMs的流行文档集[9]，我们测试了2k和8k的上下文长度。然而，Pile中包含的长度大于8k的序列很少[19]。为了评估在长上下文中的能力，我们还使用了一个名为Books3的Pile子集，该子集已被广泛用于在长上下文中训练LLMs[49,3]，并以2的倍数递增，测试了从1k到32k的上下文长度。

骨干架构。如第2.7小节所述，Transformer和Mamba使用不同的骨干架构，而TTT-Linear和TTT-MLP除非另有说明，否则总是使用Mamba骨干架构。作为消融研究的一部分，图11和图12中包含了位于Transformer骨干架构内的TTT层。当图中同时包含Transformer骨干架构和Mamba骨干架构时，我们分别用$(T)$和$(M)$来表示它们。

协议。为了确保对我们的基线模型的公平性，我们尽可能严格遵循Mamba论文中的评估协议：

• 对于每个评估设置（例如，数据集、上下文长度和方法），我们实验了四种模型大小：$125\mathrm{M}$、$350\mathrm{M}$、$760\mathrm{M}$和$1.3B$参数。对于Mamba，相应的模型大小是$130\mathrm{M}$、$370\mathrm{M}$、$790\mathrm{M}$和$1.4B$，因为Mamba不遵循Transformer的配置。
• 所有模型都使用Mamba论文中描述的Chinchilla训练方案（见附录C）进行训练。我们基于Llama架构[73]的Transformer基线也遵循Mamba论文中的基线。作为验证，我们的基线模型可以在其评估设置中复现Mamba论文中报告的数字。
• 我们没有尝试混合架构（如Griffin[18]），因为我们的基线模型不是混合的。虽然同时使用自注意力和TTT层的混合架构可能会提高性能，但它们会降低我们学术评估的清晰度。

3.1、短上下文：Pile 数据集

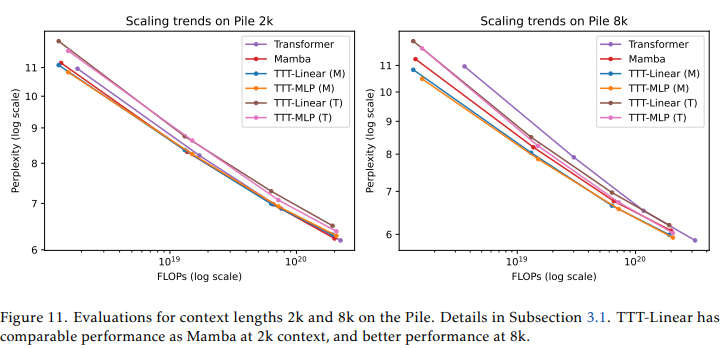
从图11中，我们可以观察到以下几点：

• 在2k上下文中，TTT-Linear (M)、Mamba和Transformer的性能相当，因为它们的线条大多重叠。在较大的浮点运算（FLOP）预算下，TTT-MLP (M)的性能稍差。尽管在每个模型大小下，TTT-MLP的困惑度都比TTT-Linear好，但额外的FLOP成本抵消了这一优势。

• 在8k上下文中，与2k时的观察结果相反，TTT-Linear (M)和TTT-MLP (M)的性能都显著优于Mamba。甚至使用Transformer骨干的TTT-MLP (T)在约1.3B参数时也略优于Mamba。我们在本文中观察到的一个稳健现象是，随着上下文长度的增加，TTT层相对于Mamba的优势会扩大。

• 在8k上下文中，Transformer在每个模型大小下仍然具有良好的（如果不是最好的）困惑度，但由于其FLOP成本较高，因此并不具有竞争力。

骨干架构的影响。将TTT层从Mamba骨干架构切换到Transformer骨干架构有两个影响。首先，到目前为止，在我们的评估中，使用Mamba骨干架构的TTT层表现更好。其次，使用Mamba骨干架构时，TTT-MLP在最佳情况下仅与TTT-Linear相当；但使用Transformer骨干架构时，TTT-MLP明显更优。我们假设，当序列建模层的隐藏状态表达能力较弱时，Mamba骨干架构中的时间卷积帮助更大。线性模型的表达能力比多层感知机（MLP）弱，因此从卷积中受益更多。我们将在下一小节中重新审视这一假设。

线性拟合不足。Chinchilla论文通过经验观察发现，遵循其训练方案的最优计算模型在FLOP与困惑度的对数-对数图中落在一条直线上，这通常也是缩放定律实验[34]中的情况。然而，我们在图11或图12（Books数据集中的类似实验）中并没有观察到清晰的线性拟合，即便是对于Transformer也是如此。考虑到数据集、上下文长度、分词器和架构之间的差异，这并不令人惊讶。遵循Mamba论文的做法，由于误差较大，我们采用连线的方式而不是线性回归来拟合这些点。{ }^{11}

3.2、长上下文：Books 数据集

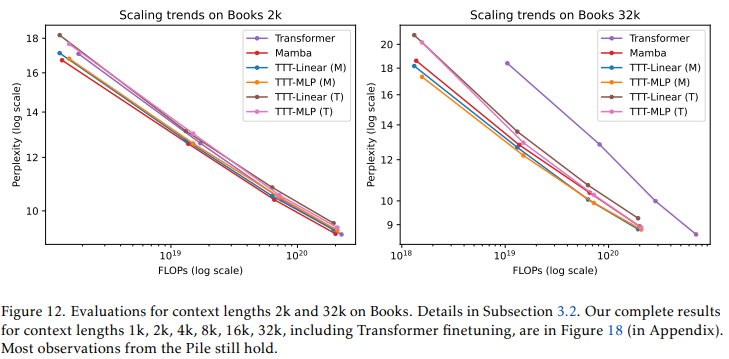
为了评估在长上下文中的能力，我们使用了一个流行的Pile子集Books3进行实验，上下文长度从1k到32k不等，每次增加2倍。这里的训练方案与Pile相同，TTT层的所有实验都在一次训练运行中完成。{ }^{12} 从图12中的部分结果中，我们可以观察到以下几点：

• 在Books数据集的2k上下文中，除了Mamba现在略优于TTT-Linear（而在Pile的2k上下文中它们的线条大致重叠）之外，Pile 2k的所有观察结果仍然成立。

• 在32k上下文中，TTT-Linear (M)和TTT-MLP (M)的表现都优于Mamba，这与Pile 8k的观察结果相似。即使在32k上下文中，使用Transformer骨干的TTT-MLP (T)也略优于Mamba。

• 在1.3B规模下，TTT-MLP (T)仅略逊于TTT-MLP (M)。如前所述，由于缺乏清晰的线性拟合，因此很难推导出经验性的缩放定律。然而，TTT-MLP (T)的强劲趋势表明，Transformer骨干可能更适合于超出我们评估范围的更大模型和更长上下文。

由于训练大型语言模型（LLMs）的成本，我们仅对2k和32k的骨干进行了消融实验。对于未来的工作，我们相信，鉴于TTT层具有更具表现力的隐藏状态，具有时间卷积的Mamba骨干将变得不再必要。

Transformer微调。虽然我们一直按照Mamba论文的方法从头开始训练Transformer，但在实践中，这种方法很少用于长上下文。标准的做法是在短上下文中训练Transformer，然后在长上下文中进行微调。为了反映这种做法，我们为4k及以上长度的上下文添加了另一个基线——TF微调。该基线从在Books 2k上根据Chinchilla方案训练的模型开始，然后按照Llama Long论文[78]的方法，使用额外$20\%$的标记在指定的上下文长度下进行微调。TF微调方案的详细信息见附录C。

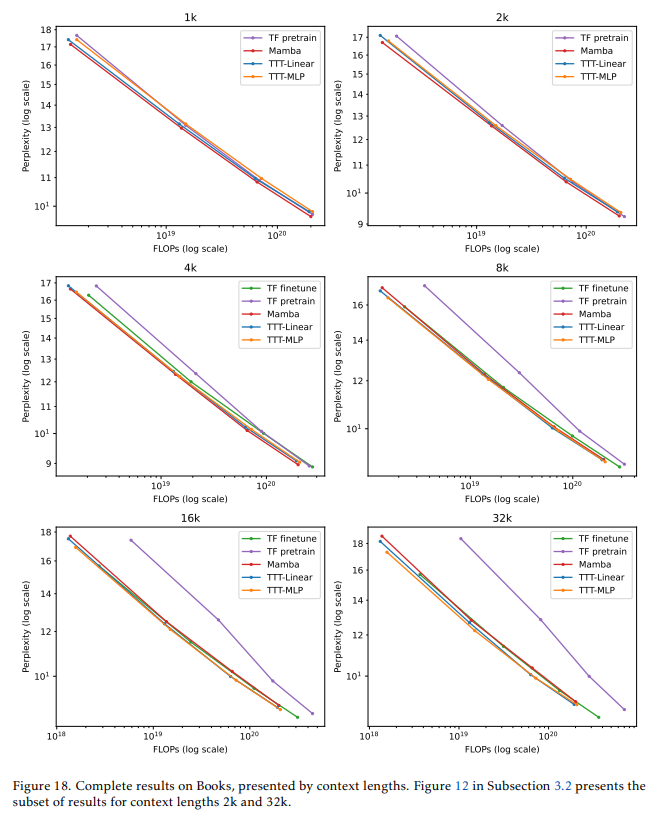
包括TF微调在内的完整上下文长度结果（1k、2k、4k、8k、16k、32k）如图18（附录中）所示。

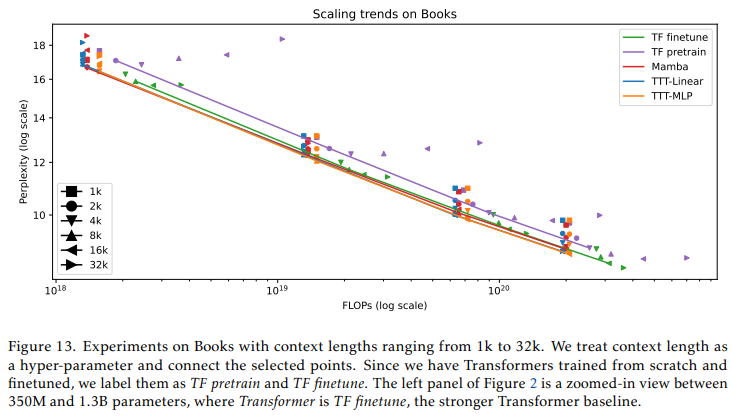
上下文长度作为超参数。虽然输入序列的长度由用户确定，但语言模型处理输入的上下文长度是由工程师作为设计选择来确定的。因此，上下文长度与其他超参数一样，是可以选择的。{ }^{13} 对于具有线性复杂性的LLMs，我们选择困惑度最小的上下文长度，因为每个上下文长度的浮点运算（FLOPs）都相同。对于Transformer来说，更长的上下文会消耗更多的FLOPs，因此我们在对数-对数图中形成所有点的凸包，并连接边界上的点。

从图13中，我们得出以下几个观察结果：

• 表现最好的TTT-Linear和TTT-MLP的线几乎完全重叠。在超过$10^{20}$ FLOPs后，Mamba和TF微调的线也大多重叠。
• TF微调的表现明显优于TF预训练，因为它受益于长上下文，而无需在训练FLOPs上产生极高的成本。请注意，TF微调和预训练的推理FLOPs同样较差，这在图中并未反映出来。
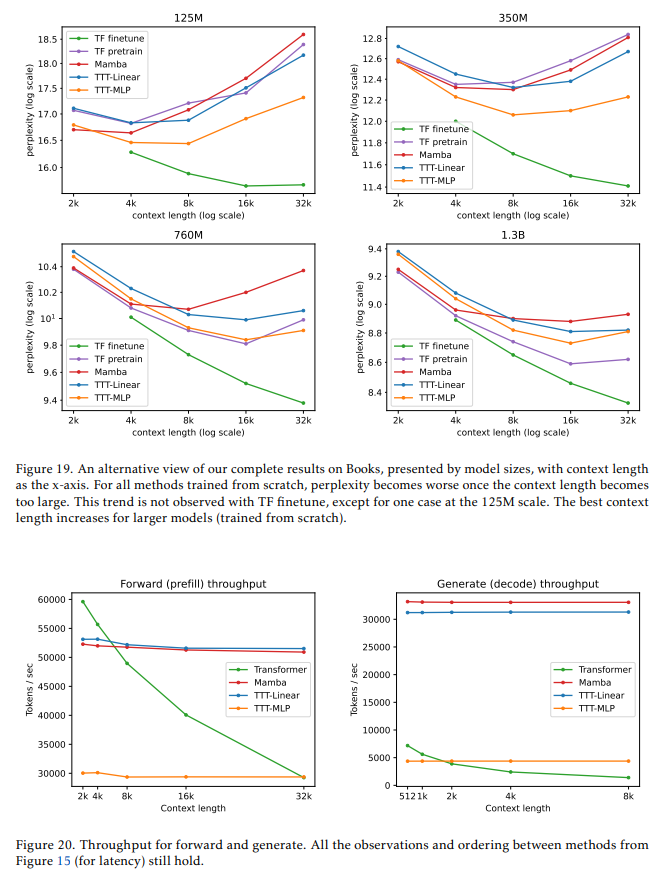
• 对于所有从头开始训练的方法（包括TF预训练），一旦上下文长度变得过大，困惑度就会变差。这一趋势在图19（附录中）中得到了突出显示。我们将对这一趋势的进一步研究留给未来的工作。
  

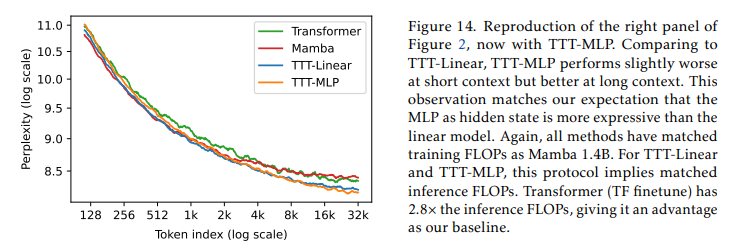
图2的左面板是图13的放大视图。为了清晰起见，我们在图2中省略了TF预训练，而只展示了TF微调（标记为Transformer），因为它是更强的基线。图14现在重现了图2的右面板，并加入了TTT-MLP和额外的讨论。

3.3、实际运行时间

大型语言模型（LLM）的训练和推理可以分解为前向传播、反向传播和生成。推理过程中的提示处理（也称为预填充）与训练过程中的前向传播是相同的操作，只是不需要为反向传播存储中间激活。由于前向传播（在训练和推理期间）和反向传播都可以并行化，我们使用对偶形式。生成新标记（也称为解码）本质上是顺序的，因此我们使用原始形式。

由于资源限制，我们的实验是用JAX编写的，并在TPU上运行。在v5e-256 TPU Pod上，Transformer基线在2k上下文的每次迭代中需要0.30秒，而TTT-Linear在每次迭代中需要0.27秒，已经比Transformer快$10\%$，且未进行任何系统优化。然而，Mamba（在PyTorch、Triton和CUDA中实现）只能在GPU上运行，因此为了公平比较，我们还对我们的方法进行了初步的系统优化，以便在GPU上运行。

具体来说，我们在ThunderKittens[66]中为前向传播编写了一个GPU内核。从历史上看，由于并行性和矩阵乘法的使用不佳，RNN在前向和反向传播过程中效率低下。我们设计前向传播内核的目标是证明小批量TTT和对偶形式在处理这些问题时的有效性。反向传播内核在效率上应具有与前向传播相同的属性，但由于需要更复杂的手动微分逻辑，因此留待未来工作。

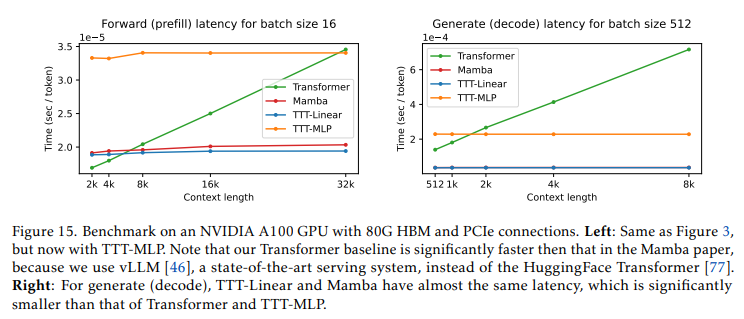
图15的左面板显示了我们的前向传播内核在批量大小为16时的延迟。所有模型的参数量均为13亿（Mamba为14亿）。随着上下文长度的增加，Transformer的每标记时间线性增长，而其他方法则大致保持不变。请注意，我们的Transformer基线明显快于Mamba论文中的基线，因为我们使用了最先进的服务系统vLLM[46]，而不是HuggingFace Transformer[77]。

此外，我们还在Triton[72]中为生成编写了另一个GPU内核，并在图15的右面板中针对批量大小为512的情况对其速度进行了基准测试。实际运行时间的另一个流行指标是吞吐量，它考虑了使用更大批量大小的潜在好处。为完整起见，我们在图20（附录中）报告了前向传播和生成的吞吐量。上述所有关于方法之间观察和排序的结论在吞吐量方面仍然成立。

4 相关工作

4.1、现代RNN

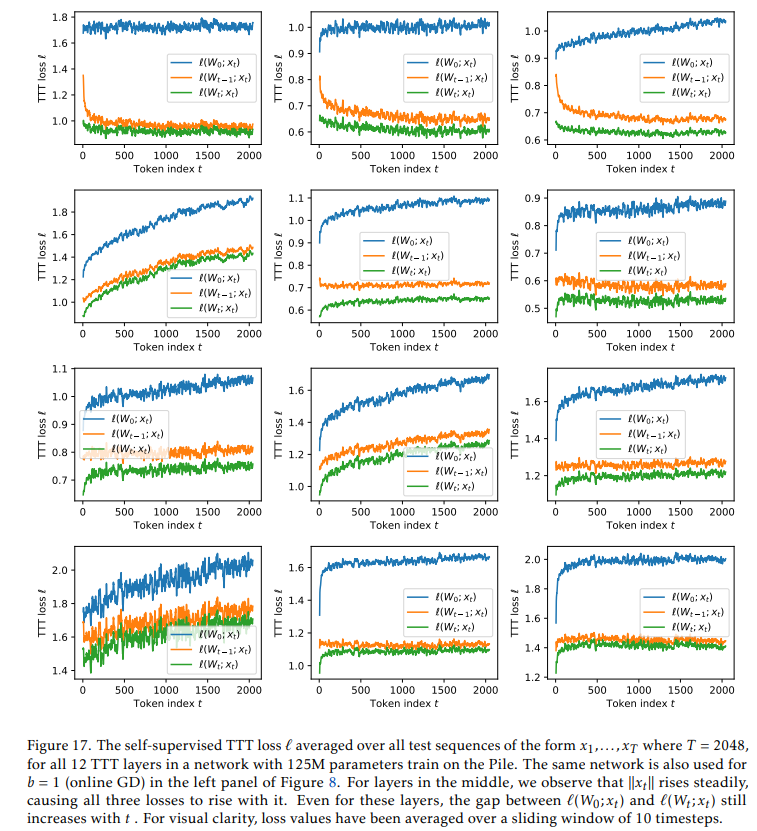
Mamba是众多结构化状态空间模型之一[27,21,57,18]。这些模型中的隐藏状态是一个向量，与LSTM类似。对于TTT-Linear或TTT-MLP，隐藏状态是一个矩阵或两个矩阵，因此更大。在图14中，我们发现TTT层可以利用其更大的隐藏状态来在长上下文中压缩更多信息，其中TTT-MLP的表现优于TTT-Linear，而TTT-Linear又优于Mamba。

与TTT-Linear类似，RWKV[55, 56]、xLSTM[5]和门控线性注意力（GLA）[79]也具有矩阵隐藏状态，这些隐藏状态继承自线性注意力[41]。现代RNN，如GLA，使用块级并行性来提高硬件效率，因此块内的标记可以通过矩阵乘法而不是累加和来处理。然而，块级并行性不会改变模型的表达能力，因为所有时间依赖性仍然等价于累加和。

相比之下，小批量TTT允许小批量之间存在更复杂的时序依赖关系。每个隐藏状态$W_t$仍然通过累加和依赖于其小批量内的先前$W$，但还通过梯度算子依赖于先前小批量中的$W$。如图8所示，小批量TTT在表达能力和硬件效率之间实现了权衡，因为较小的小批量大小$b$以较高的延迟为代价获得了更好的困惑度。这种权衡是TTT的一个独特且重要的特性。如表1所示，中间小批量大小$b=16$显著优于完全累加和的$b=T$。

4.2、测试时学习

测试时学习的思想在机器学习领域有着悠久的历史。这一思想的最早版本之一被称为局部学习（Bottou和Vapnik [10]）：对于每个测试输入，在做出预测之前先在其邻居上进行训练。这一程序已被有效地应用于从支持向量机（SVMs）[81]到现代大型语言模型（LLMs）[29]的各种模型。

测试时学习的另一个早期版本被称为转导学习[22]。正如弗拉基米尔·瓦普尼克（Vladimir Vapnik）[74]所述，转导的原则是“…获得你真正需要的答案，而不是更一般的答案。”转导学习的实际实现使用测试数据为SVMs的边界添加约束[39,17]。然而，与许多测试时训练的实例化不同，转导学习通常需要多个测试实例才能在经验上有效，而后者每次只需要一个测试实例（图像、视频或自然语言序列）。
在计算机视觉领域，测试时学习的思想已被应用于面部检测[38]、目标检测[53]、图像超分辨率[65]和3D重建[50]等应用数十年之久。最近，同样的思想也被应用于自然语言处理领域，在那里它被称为动态评估[44,45]。基本方法是直接在测试序列（通常以提示的形式出现）上对语言模型进行微调。

接下来，我们详细讨论两条相关工作线：测试时训练和快速权重。

4.2.1、测试时训练

测试时训练（TTT）的核心思想是，每个测试实例都定义了自己的学习问题，其中仅该测试实例是泛化的目标[69]。具体来说，对于每个测试实例$x$，传统做法是使用针对所有训练实例平均优化的预测器$f$来预测$f(x)$。TTT首先根据$x$制定一个学习问题，然后在$x$上训练模型$f_x$（通常使用$f$作为初始化），并预测$f_x(x)$。

由于测试实例没有标签，因此学习问题只能通过自监督任务来制定。先前的工作表明，使用重建的TTT显著提高了性能，特别是在处理异常值方面[23]。当在流式到达的视频帧上进行测试且TTT是自回归的[76]时，改进效果更加明显，因为$f_t$是在过去的帧$x_1,\dots ,x_t$上训练的。自回归连接使得[76]与我们的论文最为相关。

从概念上讲，我们的论文与先前工作的最大区别在于，我们的重建任务是在外部循环中学习的，而不是通过人为先验手工设计的。TTT的后续工作探索了诸如机器人操作[28]和行走[68]等应用，这些应用通常需要对自监督任务进行不同的设计。

4.2.2、快速权重

快速权重的一般思想是在仅与最相关数据上更新“快速”模型的参数，这与在所有数据上更新“慢速”模型的常规做法相反[71]。这一思想自20世纪80年代就已存在[32]。最相关的数据可以是测试实例本身，因此TTT可以看作是快速权重的一个特例。

在快速权重的先前工作中，通常避免形成优化数据上某些目标的显式学习问题。例如，赫布学习（Hebbian learning）和霍普菲尔德网络（Hopfield networks）的更新规则[35]只是简单地将$x{x}^T$（或其某种变体）[4]添加到每个输入$x$给定的快速权重上。相比之下，TTT采纳了制定显式学习问题的思想，其中测试实例是泛化的目标。我们的更新规则也是优化过程中的一个明确步骤。

快速权重程序员（FWP）的思想是用一个“慢速”模型来更新快速权重[62]。我们的内循环权重$W$可以看作是“快速”的，而外循环权重$\theta$可以看作是“慢速”的。因此，包含TTT层的网络可以看作是FWP的一个特例[43]，这与TTT可以看作是快速权重的一个特例类似。具有上述赫布更新规则的FWP等价于线性注意力[60]，因此也等价于使用批量梯度下降的朴素TTT-Linear。

快速权重程序员（FWP）的定义非常广泛。实际上，所有具有某些门控机制的网络，如带有SwiGLU块的Transformer[63]，也可以看作是FWP的一个特例${}^{16}$。最近的研究一直在尝试将FWP应用于语言建模：Irie等人[37]设计了以“慢速”网络输出为权重的“快速”网络。Clark等人[16]为Transformer添加了一层快速权重作为最终层，其初始化被训练为慢速权重。我们相对于现有FWP工作的贡献再次在于为更新制定了显式的学习问题，这使我们能够借鉴学习中的工具，如小批量和层归一化（LN）。

4.3、学会学习

几十年来，研究人员一直在争论，学会学习（也称为元学习或双层优化）应该是智能的一个关键组成部分[61, 6, 70, 47]。在先前的工作如[2]、[20]和[52]中，内循环一次从整个数据集中学习，而不是从序列中学习，因此外循环需要一组数据集或任务。简而言之，外循环位于常规训练的“上一级”。由于很难收集数百万个数据集，因此外循环很难扩展。

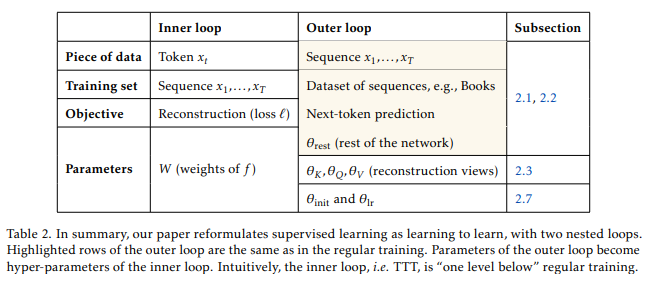
相比之下，对于TTT，每个序列本身就是一个数据集，并定义了自己的泛化问题。内循环位于常规训练的“下一级”，因此我们的外循环只是监督学习典型问题的另一种解决方案，而不是像跨数据集泛化这样的新问题设置。如表2所示，我们的外循环与常规训练处于“同一级别”。这使得我们的外循环更容易扩展。

5、讨论

我们已经将监督学习的典型问题重新表述为学习在测试时进行学习。我们的表述为构建传统上称为网络架构的内容提供了一个替代性的概念框架。我们在表2中总结了当前的实例化。

在这个框架内，有效实例化的搜索空间是巨大的，而我们的论文只是迈出了一小步。幸运的是，如果我们的观点成立，那么常规训练中的启发式方法可以转移到测试时训练，并且搜索可以高效进行。接下来，我们概述了未来工作中一些特别有前景的方向。

• 外循环参数化。有许多其他方法来参数化一系列多视图重建任务，或者可能是更一般的自监督任务族。如果我们尝试的第一个就证明是最好的，那将是一个巨大的巧合。

• 系统优化。我们在3.3小节中的系统优化充其量只是初步的，并且有很多方法可以改进它。此外，通过时间的流水线并行性可能允许我们在多个设备上一起处理数百万个标记的长序列。

• 更长的上下文和更大的模型。受我们学术资源的限制，我们还没有在数百万或数十亿长度的上下文中进行训练，而根据图19，这也需要更大的模型。在更长的上下文中，TTT层的优势应该变得更加明显。

• $f$的更高远的实例化。当上下文长度变得更长时，$f$也需要变得更大。对于视频任务和实体代理，其上下文长度可以很容易地扩展到数百万或数十亿，此时$f$可能是一个卷积神经网络。

• 多级学习以学习。如果$f$本身是一个自注意力层，那么根据定理2，它可以被解释为另一个嵌套在现有内循环中的内循环。以这种方式，我们有可能构建多级的嵌套学习问题。

为什么我们研究TTT？首先，一个更基本的问题：为什么研究人工智能？对于我们中的一些人来说，人工智能是一个探索人类智能本质的游乐场。先前的工作经常尝试用机器学习来模拟人类学习，其中训练是在一个包含独立同分布（i.i.d.）实例的打乱数据集上进行的，而推理则是在一个独立的测试集上进行的。然而，人类并不自然地通过i.i.d.实例学习，也没有训练集和测试集的划分。我们认为，人类学习与TTT，即我们的内循环，有着更有前途的联系，因为内循环的数据是一个可能非常长的、具有强时间依赖性的序列，任何数据片段都可以同时用于训练和测试。这就是我们研究TTT的原因。

A、对偶形式

本节的目的是推导出具有非线性激活函数的任意深度多层感知机（MLP）的对偶形式。

不失一般性，为了方便起见，我们设 $\eta =1$，并仅考虑第一个小批量，其中 $t=1,\dots ,b$。记

${\hat{x}}_t={\theta }_K{x}_t,y_t={\theta }_V{x}_t,{\bar{x}}_t={\theta }_Q{x}_t$

同时，记 $\hat{X}=\left[{\hat{x}}_1,\dots ,{\hat{x}}_b\right]$，以及类似地定义 $Y$ 和 $\bar{X}$。一般来说，大写字母表示矩阵，其列是由相应的小写字母表示的向量。

对于一个有 $K$ 层的网络，我们用 $W_0^k$ 表示第 $k$ 层的初始参数。我们的约定是使用上标表示层，下标表示时间。

A.1、前向传播

在TTT（Test-Time Training）的初始前向传播过程中，我们用 ${\hat{X}}^k=\left[{\hat{x}}_1^k,\dots ,{\hat{x}}_b^k\right]$ 表示第 $k$ 层的输入，其中 ${\hat{X}}^1=\hat{X}$。现在我们使用这些符号来编写TTT的前向传播过程。

对于 $k=1,\dots ,K$：

• $Z^k=W_0^k{\hat{X}}^k$
• ${\hat{X}}^{k+1}={\sigma }_k\left(Z^k\right)$
  其中，对于 $k=1,\dots ,K$，${\sigma }_k$ 可以是任何逐元素操作（$\mathbb{R}\mapsto \mathbb{R}$），其导数为 ${\sigma }^{\prime }$。

给定 ${\hat{X}}^{K+1}$，我们计算损失：

$l=\frac{1}{2}\ell \left(W_0^1,\dots ,W_0^K;\hat{X}\right)=\frac{1}{2}{\Vert {\hat{X}}^{K+1}-Y\Vert }_F^2={\sum }_{t=1}^b{l}_t$

其中，$l_t=\frac{1}{2}{\Vert {\hat{x}}_t^K-y_t\Vert }^2$ 与方程4中定义的相同，只是为了方便起见除以了 $1/2$。上述所有操作（除了 $\sigma$）都是矩阵乘法和求和，因此在硬件上非常高效。原始形式和对偶形式都共享这些初始操作。

A.2、原始形式

原始形式首先计算 $G_t^k={\nabla }_{W_0^k}{l}_t$ 对于 $t=1,\dots ,b$，然后更新 $W_t^k=W_0^k-{\sum }_{s=1}^t{G}_s^k$。最后，给定 ${\bar{X}}^1=\left[{\bar{x}}_1^1,\dots ,{\bar{x}}_b^1\right]=\bar{X}$，原始形式使用更新后的 $W$ 重复前向传播过程。

对于 $k=1,\dots ,K$：

• ${\bar{z}}_t^k=W_t^k{\bar{x}}_t^k$，对于 $t=1,\dots ,T$
• ${\bar{x}}_t^{k+1}={\sigma }_k\left({\bar{z}}_t^k\right)$，对于 $t=1,\dots ,T$
  其中，${\bar{X}}^{K+1}=\left[{\bar{x}}_1^{k+1},\dots ,{\bar{x}}_b^{k+1}\right]$ 包含输出标记。

请注意，标准的反向传播仅计算梯度的和：

${\nabla }_{W_0^k}l={\sum }_{t=1}^b{\nabla }_{W_0^k}{l}_t={\sum }_{t=1}^b{G}_t^k$

因此，对于 $t=1,\dots ,b$，求和中的各个项 $G_t^k$ 的计算不能合并成矩阵乘法。类似地，原始形式中的前向传播对每个 ${\bar{x}}_t$ 使用不同的 $W_t$，因此也不能像标准前向传播那样以相同的方式进行批量处理。这些非标准传播过程的硬件效率较低。

A.3、对偶形式

如第2.5小节所述，对偶形式的目标是仅通过矩阵乘法和轻量级操作（如求和、$\sigma$ 和 ${\sigma }^{\prime }$）来计算 ${\bar{X}}^{K+1}$ 和 $W_b^1,\dots ,W_b^K$。为了实现这一目标，我们避免显式计算中间变量：$G_t^k$ 和 $W_t^k$ 对于 $t=1,\dots ,b$。

对偶形式首先计算 ${\nabla }_{{\hat{X}}^{K+1}}l={\hat{X}}^{K+1}-Y$，然后进行标准的反向传播。

对于 $k=K,\dots ,1$：

• ${\nabla }_{Z^k}l={\sigma }_k^{\prime }\left({\nabla }_{{\hat{X}}^{k+1}}l\right)$
• ${\nabla }_{{\hat{X}}^k}l={\left(W_0^k\right)}^T{\nabla }_{Z^k}l$
• ${\nabla }_{W_0^k}l={\nabla }_{Z^k}l{\left({\hat{X}}^k\right)}^T$

现在我们可以计算 $W_b^k=W_0^k-{\nabla }_{W_0^k}l$。为了计算输出标记，我们再进行一次前向传播。

对于 $k=1,\dots ,K$：

• ${\bar{Z}}^k=W^k{\bar{X}}^k-{\nabla }_{Z^k}l\cdot \mathrm{mask}\left({\left({\hat{X}}^k\right)}^T{\bar{X}}^k\right)$
• ${\bar{X}}^{k+1}=\sigma \left({\bar{Z}}^k\right)$

在前向传播结束时，我们已经计算出了 ${\bar{X}}^{K+1}$。

虽然这种前向传播是非标准的，但它仅包含矩阵乘法、求和、$\sigma$ 和掩码操作，因此与标准前向传播一样高效。

A.4、推导

为了推导出对偶形式，我们证明：

${\bar{Z}}^k=W^k{\bar{X}}^k-{\nabla }_{Z^k}l\cdot \mathrm{mask}\left({\left({\hat{X}}^k\right)}^T{\bar{X}}^k\right)$

与在原始形式中计算的结果相同。具体来说，我们证明在对偶形式的前向传播中，${\bar{Z}}^k$ 的每一列 ${\bar{z}}_t^k$ 等于原始形式前向传播中的 $W_t^k{\bar{x}}_t^k$。我们引用一个简单的事实。

事实1. 定义矩阵 $A=\left[a_1,\dots ,a_b\right],Q=\left[q_1,\dots ,q_b\right]$，和 $V={\left[v_1,\dots ,v_b\right]}^{17}$。定义 ${\hat{v}}_t={\sum }_{s=1}^t{a}_s^T{q}_t{v}_s$，以及 $\hat{V}=\left[{\hat{v}}_1,\dots ,{\hat{v}}_b\right]$，则 $\hat{V}=V\cdot \mathrm{mask}\left(A^{T}Q\right)$。

现在，将 $A={\hat{X}}^k,Q={\bar{X}}^k,V={\nabla }_{Z^k}l$，和 $\hat{V}=W^k{\bar{X}}^k-{\bar{Z}}^k$ 代入上述事实中，我们已经证明了所需的等式。

请注意，上面使用的 ${\sigma }_k$ 和 ${\sigma }_k^{\prime }$ 可以扩展到不一定是逐元素操作的任意函数，包括归一化层。这种扩展可以通过标准自动微分库（如JAX和PyTorch）中的vjp（向量-雅可比积）来实现。然而，对偶形式不能加速 $\sigma$ 或其vjp内部的操作。

B、Nadaraya-Watson 估计量

Nadaraya-Watson 估计量的推导。在本节中，我们使用 $\mathbf{x}$ 来表示输入标记 $x$ 作为随机变量。我们期望的输出是相应的输出标记，即另一个随机变量 $\mathbf{z}$。这被表述为估计 $\mathbf{z}$ 的条件期望：

$\mathbb{E}[\mathbf{z}\mid \mathbf{x}=x]=\int p(z\mid x)zdz=\int \frac{p(x,z)}{p(x)}zdz$

由于真实的概率分布 $p(x)$ 和 $p(x,z)$ 是未知的，我们用它们的核密度估计来替代。具体来说，$p(x)$ 的核密度估计是：

$\hat{p}(x)=\frac{1}{n}{\sum }_{i=1}^n\kappa \left(x,x_i\right)$

其中，每个 $x_i$ 通常是训练数据中的一部分。（回顾我们的论文，$x_i$ 特别是内循环的训练数据，即一个标记，这符合我们在正文中使用的符号。）

为了估计 $p(x,z)$，我们使用乘积核：

$\hat{p}(x,z)=\frac{1}{n}{\sum }_{i=1}^n\kappa \left(x,x_i\right){\mathcal{K}}^{\prime }\left(z,z_i\right)$

乍一看，将联合概率分解为两个看似独立的核似乎很荒谬。但在这个情况下，${\kappa }^{\prime }$ 实际上可以是任何依赖于 $x_i$ 的 ${\kappa }_i^{\prime }$，因为它将被积分掉。因此，这两个核不需要是独立的。

将这些估计代入，我们得到 Nadaraya-Watson 估计量：
$$\begin{array}{rl}\hat{E}[\mathbf{z}\mid \mathbf{x}=x]& =\int \frac{\hat{p}(x,z)}{\hat{p}(x)}zdz\\ & =\frac{1}{\hat{p}(x)}\int \hat{p}(x,z)zdz\\ & =\frac{1}{{\sum }_{i=1}^n\kappa \left(x,x_i\right)}\int \sum _{i=1}^n\kappa \left(x,x_i\right){\kappa }^{\prime }\left(z,z_i\right)zdz\\ & =\frac{1}{{\sum }_{i=1}^n\kappa \left(x,x_i\right)}\sum _{i=1}^n\kappa \left(x,x_i\right)\int {\kappa }^{\prime }\left(z,z_i\right)zdz\\ & =\frac{1}{{\sum }_{i=1}^n\kappa \left(x,x_i\right)}\sum _{i=1}^n\kappa \left(x,x_i\right)z_i.\end{array}$$

非对称核。 在现代，人们认为核应该是正半定的，但这对于$\kappa$来说可能无法保证，除非${\theta }_K={\theta }_Q$。然而，几十年前在核函数领域工作的人们，大约在Nadaraya-Watson估计器流行的时候，对核函数的选择非常宽松，像我们方程9中的$\kappa$这样的非对称核有着悠久的传统：当核估计器使用${\theta }_K\ne {\theta }_Q$时，它被称为气球估计器[15]。诸如Breiman等人的论文[11]甚至将${\theta }_Q$作为$x^{\prime }$的函数，这被称为样本自适应平滑。

C、实验细节

架构。 我们的Transformer严格遵循Mamba论文中的构造，其中Transformer被称为Transformer++。具体来说，Transformer架构基于Llama[73]，使用旋转位置编码（RoPE）[67]、SwiGLU MLP块[63]和RMSNorm[80]替代LayerNorm。我们的Mamba基线使用作者提供的公开代码。我们已经验证过，我们的基线可以复现[26]中报告的数字。

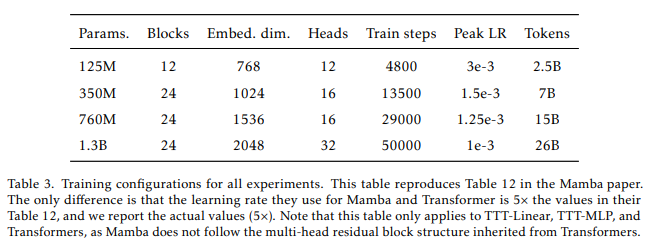
训练配置。 我们的训练配置在表3中，它简单地复现了Mamba论文中的表12。如脚注12所述，所有模型均以0.5M标记的批量大小进行训练，无论上下文长度如何。我们所有的优化超参数都遵循Mamba论文附录E.2中的“改进方案”，具体如下：

• AdamW优化器：$\beta =(0.9,0.95)$
• 余弦调度：衰减至最终学习率$1e-5$
• 训练步骤的$10\%$期间进行线性学习率预热
• 权重衰减：0.1
• 梯度裁剪：1.0
• 无Dropout
• 混合精度

如脚注10所述，所有模型都使用Llama分词器[73]进行训练。对于在Pile上的实验，这与Mamba论文中的方法唯一的区别是后者使用了另外两个分词器。对于在Books上的实验，我们发现RoPE编码[67]的原始角度$\theta =10,000$对于我们的Transformer基线在长上下文中不是最优的。从上下文长度4k开始，我们根据Llama Long论文[78]尝试$\theta =500,000$，并为Transformer（包括预训练和微调）使用更好的困惑度。

Transformer微调。微调使用与从头开始训练时相同的优化超参数开始新的余弦调度，但峰值学习率除外。我们尝试了三个峰值学习率进行微调：$1e-5$、$1e-4$和$1e-3$，并选择最佳困惑度。我们观察到，对于125M模型，$1e-4$效果最好，而对于350M及更大模型，$1e-5$效果最好。考虑到Chinchilla方法的最终学习率为$1e-5$，这一观察结果是合理的。

TTT的学习率。如第2.7小节所述，TTT-Linear的内环基础学习率${\eta }_{\text{base }}$设置为1，TTT-MLP的设置为0.1。我们设置${\eta }_{\text{base }}$的启发式方法与人们为常规训练设置外环学习率的方法类似：我们尝试了 η base  ∈ { 0.01 , 0.1 , 1 , 10 } \eta_{\text {base }} \in\{0.01,0.1,1,10\} ηbase ​∈{0.01,0.1,1,10}，并使用了不会导致不稳定性的最大值。对于TTT-MLP，我们在训练步骤的$10\%$期间对${\eta }_{\text{base }}$进行线性预热，这与常规训练类似。内环中的训练步数是$T/b$（假设可除）。对于TTT-Linear，我们尝试在内环中进行线性预热，但没有观察到差异。

图2（右）和图14中的实验。为了确保对Mamba的公平性，这些实验中的所有方法都匹配了训练浮点运算次数（FLOPs），并且使用与Mamba 1.4B相同的训练方案（表3的最后一行）进行训练。为了与Mamba的FLOPs相匹配，Transformer有19个块而不是24个。对于TTT-Linear和TTT-MLP，它们的FLOPs已经接近Mamba的FLOPs，因此我们将MLP块的隐藏维度从5504更改为5808（TTT-Linear）和5248（TTT-MLP）。

随时间进行梯度检查点。默认情况下，像JAX和PyTorch这样的库会保存前向传播过程中的中间激活，以便在后向传播过程中重用它们。然而，对于一个隐藏状态为$W$的TTT层，这种默认设置会保存$W_1,\dots ,W_T$，这会占用太多内存。使用TTT小批量和双重形式，我们仍然需要在小批量结束时保存（假设可除）$\kappa =T/b$个$W$。在这种情况下节省内存的一种标准技术是梯度检查点[13]，它通常应用于层之间，但我们将其应用于时间维度上。