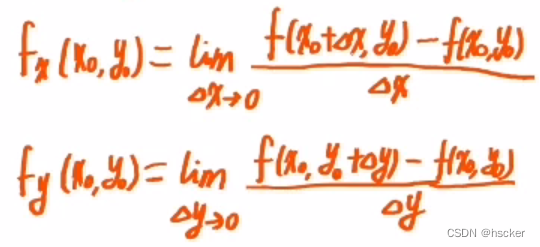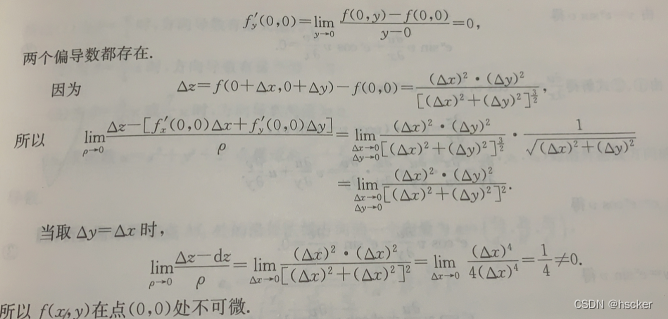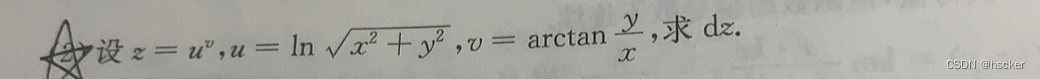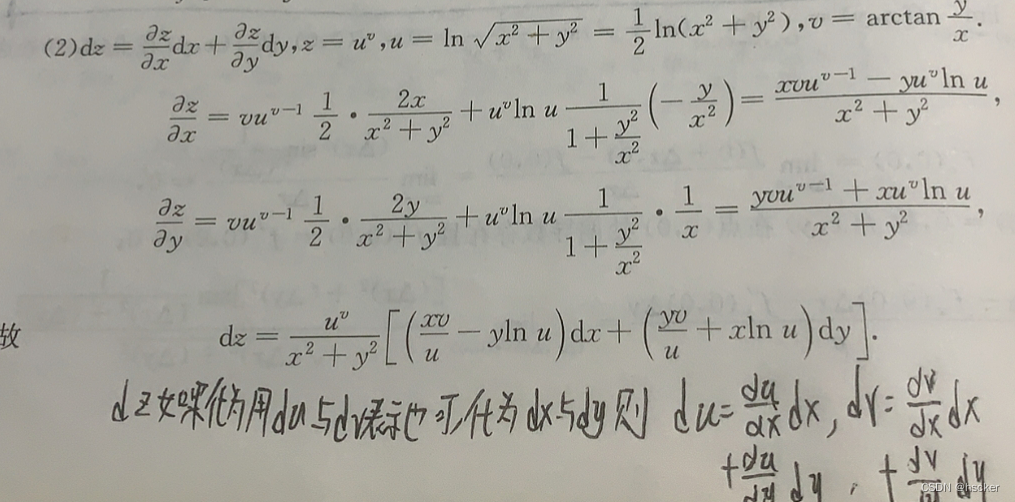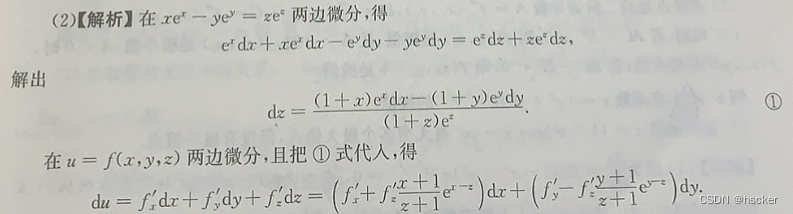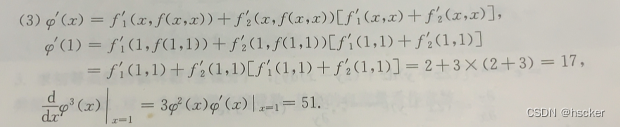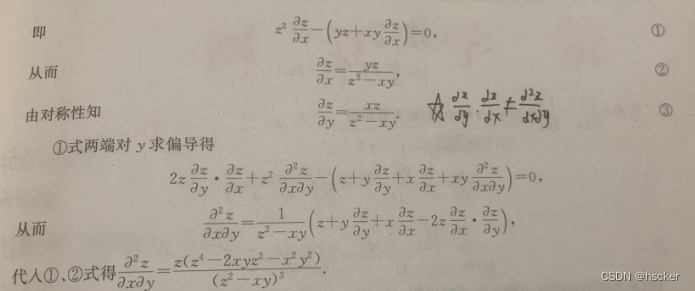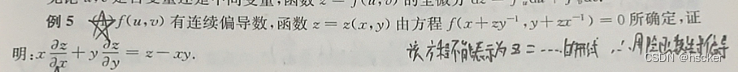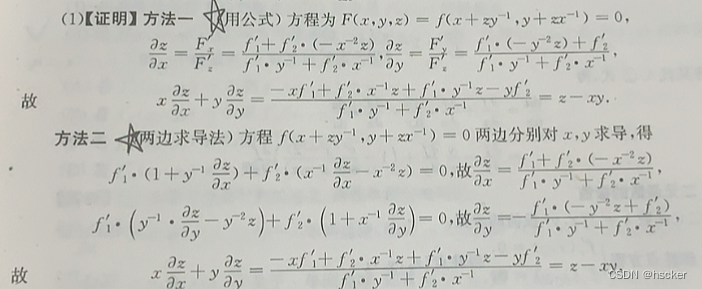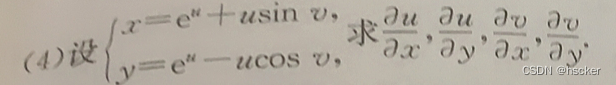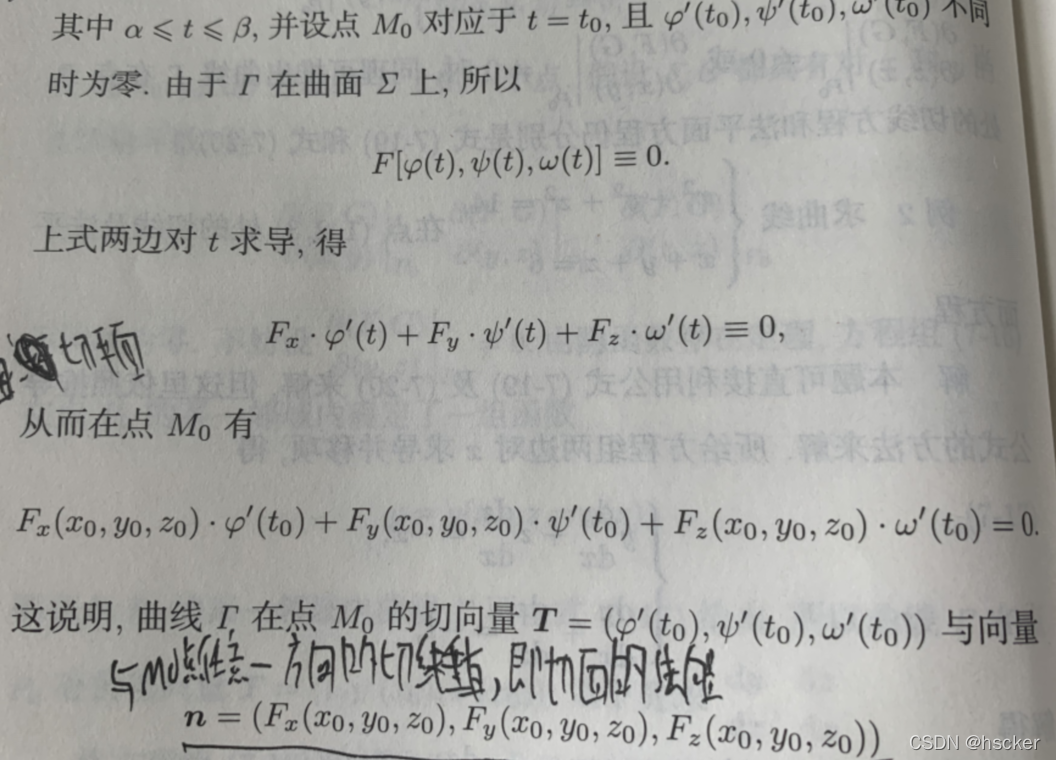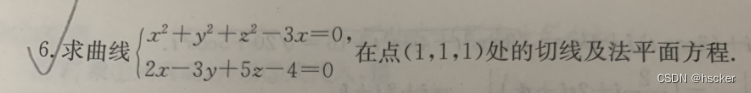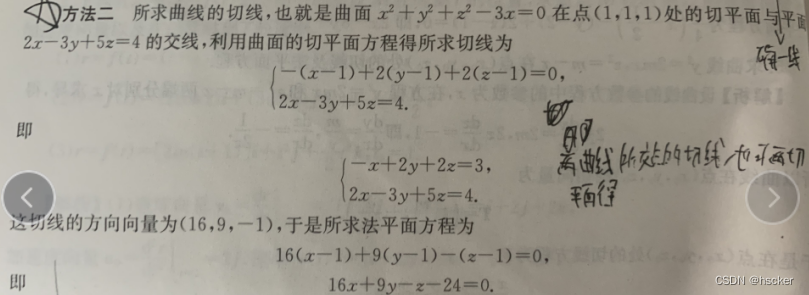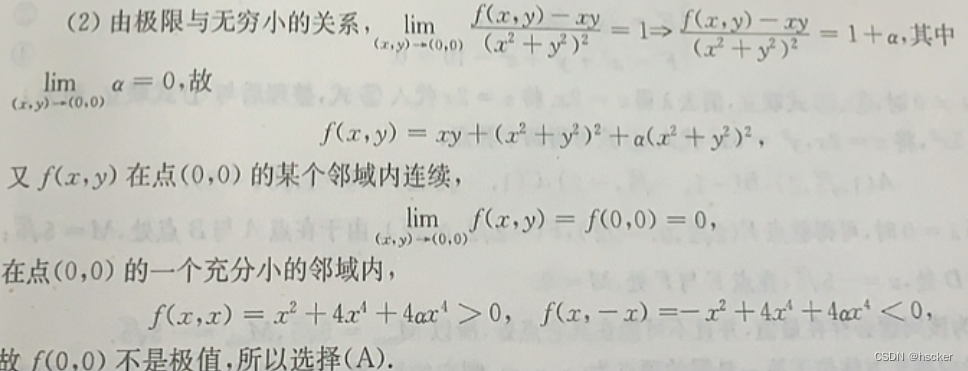目录
一、多元函数的极限与连续
(1)多元函数的二重极限
1、证明函数的极限是否存在:
(1) 定义证明:与一重极限相似,x之间的距离无限逼近变为点(x,y)与聚点的距离无限逼近,
即当满足式子 0<<任意正数的任意点都有
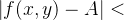
则A为,点趋近(x0,y0)时的极限(可以理解为一对点值的差距都无限小时,点逼近于点,值也逼近于值,并且各个方向都这样,那么极限存在)
(2)设y与x的函数证明极限不存在:由于在x,y平面内进行趋近,所以可以设y=kx,把y替代为x,算出结果来判断极限的结果如果与k有关,则极限不唯一,则不存在,反之与k无关也不能证明存在(因为可以沿着曲线接近,所以绝对不能用这个方法求极限)
2、求多元函数的极限:
(一重极限的求极限方法同样可以套用于二重极限,无非就是多了个自变量,把x和y看作一个整体变量z,合二为一即与一重极限求法一模一样)
(1)可以利用等价无穷小代换
例1、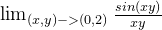
(2)如果只含有xy这一类型变量可以设xy为t,根据x,y的趋近值求出t的趋近值后,化为一重极限来做
(3)可以利用夹逼定理
(2)多元函数的连续性
1、趋于某个点的极限值等于那个点的函数值,则函数在这个点连续
2、有界闭区域D上的连续多元函数必能在d上最大值与最小值间的任何数
二、偏导数与全微分
1、几何意义上来看,求x的偏导数就是求对于x轴的倾角
2、可微的必要条件,函数的一阶偏导数连续(偏导数存在则原函数连续),则这个点可微(函数连续,才可以在这个点微分,导函数连续才可以利用公式求出微分的值,不然求不出就等于不可微)
3、可微充分条件,函数的偏导数在这个点连续(这样此点就不会是尖点,而是平滑的点,那就可以造出对应的切平面),则该点可微
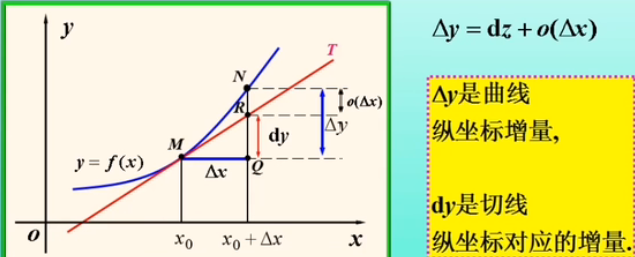
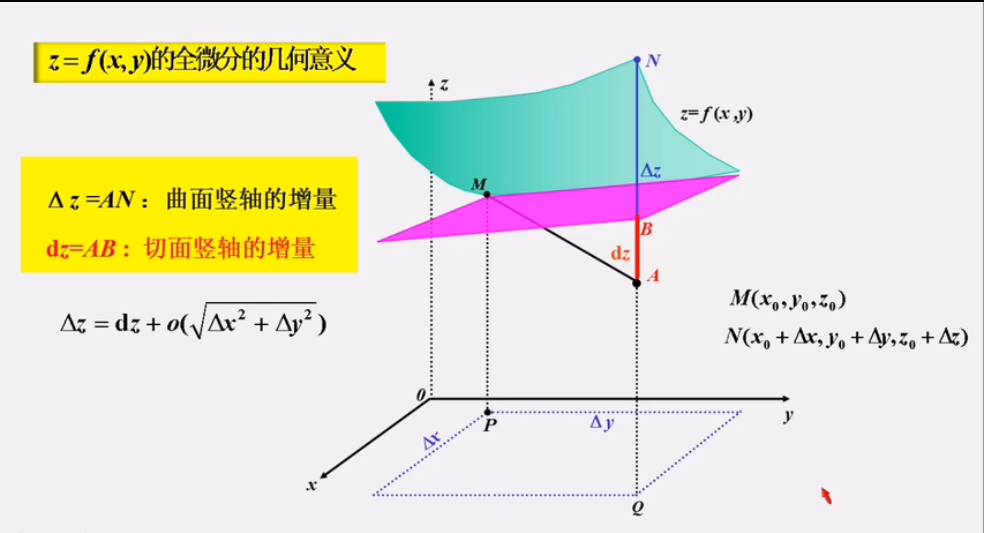
4、全微分和一元函数微分的几何意义
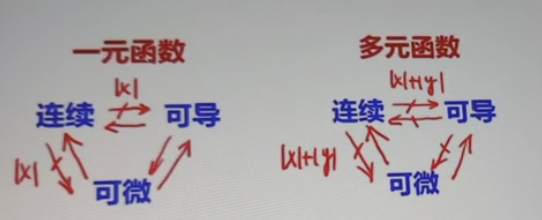
5、一元函数和多元函数可微,可导,连续之间的联系
(唯一不同的就是多元函数的可导推不出连续与可微,因为多元函数的可导是偏导,只有两个方向,而多元函数的连续与可微要求各个方向的导数存在,即一阶偏导数存在且原函数在这个点连续)
6、证明某点偏导数的存在
(1)如果是分段函数,不可以直接对方程求偏导,因为那个点不在函数定义域内,这时只能利用偏导数的定义来证明(即求极限来证明)
(2)如果不是分段函数,则直接对函数求偏导看偏导数是否有意义
7、可微的充分条件=二元函数的偏导数存在(偏导数仍然是关于点的函数)
例1 (3y)^y要化为e的指数形式来求导,3y不是整数
例2 利用全增量和全微分的差与x,y变化量之比的极限值是否为0来判断函数能否微分
例3 求函数的全微分
例1 (化至最简形式,显函数中的du与dv转为dx与dy)
例2 (化至最简形式,隐函数中的dz转为dx与dy)
三、多元复合函数的求导法则
1、抽象函数的二阶偏导数(函数的偏导数跟函数有一样的连接式)
例1
例2 套娃的抽象函数求导
四、隐函数的求导公式
1、求导公式: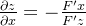
2、方程组情形:(分母由偏导数的系数组成,分子根据求的偏导数的分母在把那一列替换为方程右边的系数,偏导数的结果可以含有u与v不一定只有x与y)
3、不能利用公式求导的隐函数,直接对等式两边进行求导
例1 (求二阶导数,一阶可以用公式,二阶只能等式两边同时对x求导,在把一阶的结果代入得到最终的结果)
例2
例3 抽象隐函数的求偏导
4、雅克比行列式求解隐函数方程组
五、多元函数微分学的几何应用
(1)空间曲线的的切线与法平面
1、将曲线的x,y,z由t来表示或者由x来表示,求出这三个函数的导数,三个导数所形成的的向量即为曲线的方向向量(即x,y,z三方向的导数结合即为曲线主方向的导数,主方向的导数方向向量可以在三维坐标中被分解为3个方向,注意不可以是偏导数)
(方向向量也可以用,方程组求出的dx,dy,dz求)
(2)曲面的切平面与法线
可以看出过曲面上一点M的所有切向量总是与向量n垂直,所以n为该点切面(这时是曲面而不是曲线所以是切面不止一条切线)的法向量
例1
这题除了对x求导后利用雅克比行列式硬算出x,y,z的对x导数方程外,也可以利用两个切平面来表示两个曲面相交的点的切线(两面确一线)
六、方向导数与梯度
(1)方向导数:
1、可微则该点方向导数一定存在,方向导数公式为(方向导数即沿某一方向的距离变化率)
(由式可得,一点一方向确定一个方向导数)
例1 (方向导数=方向余弦+偏导数向量,二者相乘得到值,所以方向导数是值)
(梯度=x,y,z三个方向的变化率,即偏导数向量,所以梯度是向量)
(2) 梯度:
梯度本身是一个向量,方向导数可以由梯度和单位向量的数量积表示(此时方向导数不是一个向量,所以符合)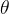
(当梯度代表的导数向量和单位向量方向一致时,即这个方向是这个点方向导数变化最快的方向,即距离变化率最大的地方)
七、多元函数的极值及其应用
1、极值的充分与必要条件
可以用充分条件判断是否有极值,极值对应的点必定是驻点
例1
例2 根据极限判断一点是否为极值点
2、条件极值 拉格朗日乘数法
1、拉格朗日乘数法:
1、当附加条件简单时,可以直接将原函数从二元函数换为1元函数求求导
2、应用题的拉格朗日函数设法
3、拉格朗日函数法的约束条件