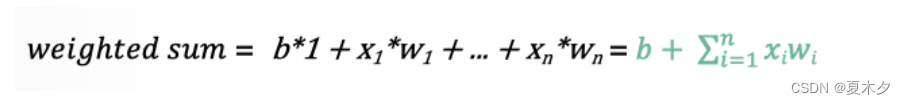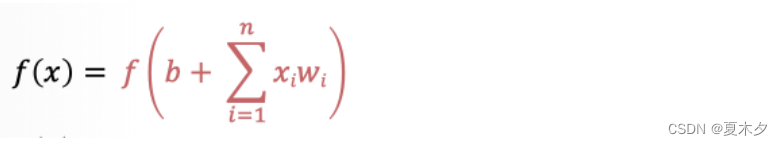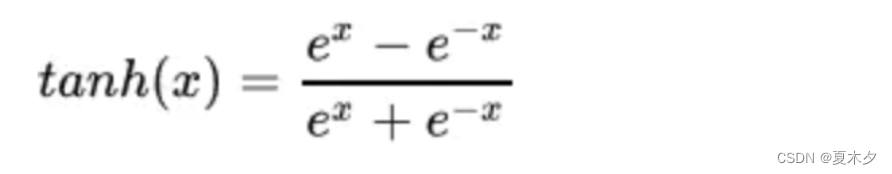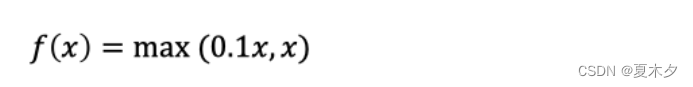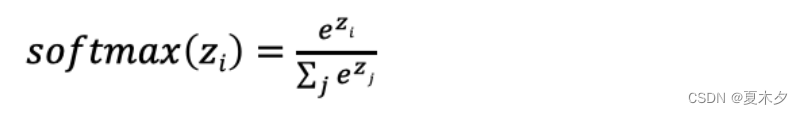神经元与神经网络
1 什么是神经网络和神经元
人工神经网络(英语:Artificial Neural Network,ANN),简称 神经网络(Neural Network,NN)或 类神经网络,是一种模仿生物神经网络(动物的中枢神经系统,特别是大脑)的结构和功能的数学模型,用于对函数进行估计或近似。
人脑可以看做是一个生物神经网络,由众多的神经元连接而成。当神经元“兴奋”时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了一个“阈值”,那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质。
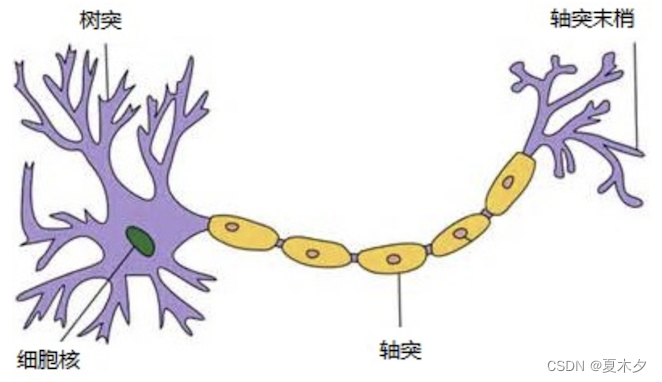
在生物神经网络中,每个神经元与其他神经元相连。各个神经元传递复杂的电信号,树突接收到输入信号,然后对信号进行处理,通过轴突输出信号。生物神经元如下图:
那怎么构建人工神经网络中的神经元呢?
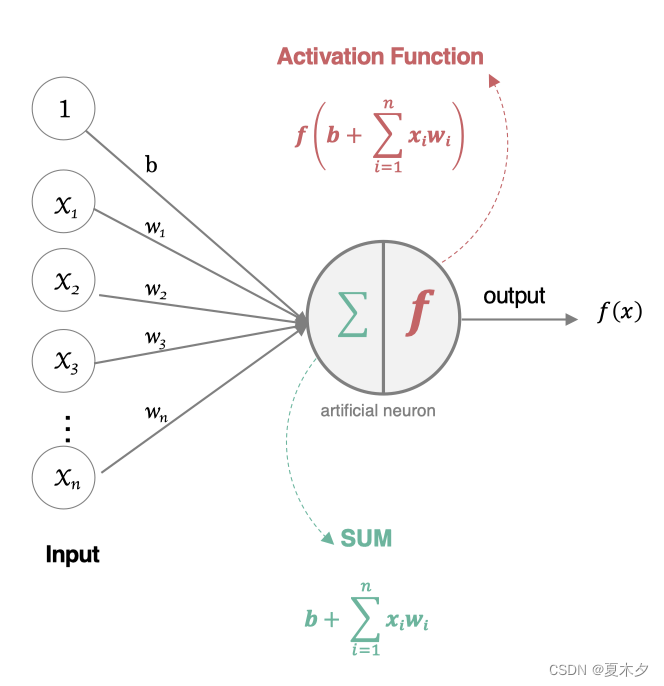
受生物神经元的启发,人工神经元接收来自其他神经元或外部源的输入,每个输入都有一个相关的权值(w),它是根据该输入对当前神经元的重要性来确定的,对该输入加权并与其他输入求和后,经过一个激活函数 f,计算得到该神经元的输出。
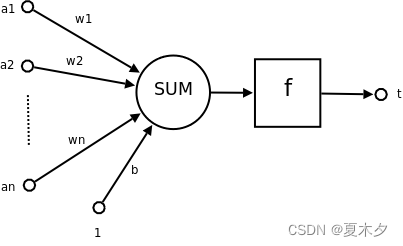
一个简单的神经元如下图所示:
其中:
- a 1 , a 2 ⋯ a n a_1,a_2\cdots a_n a1,a2⋯an 为各个输入的分量
- w 1 , w 2 ⋯ w n w_1,w_2 \cdots w_n w1,w2⋯wn 为各个输入分量对应的权重参数
- b b b 为偏置
- f f f 为激活函数,常见的激活函数有tanh,sigmoid,relu
- t t t 为神经元的输出
使用数学公式表示就是:
t
=
f
(
W
T
A
+
b
)
t = f(W^TA+b)
t=f(WTA+b)
可见,一个神经元的功能是求得输入向量与权向量的内积后,经一个非线性传递函数得到一个标量结果。
1943 年,McCulloch 和 Pitts 将上述情形抽象为上图所示的简单模型,这就是一直沿用至今的 M-P 神经元模型。把许多这样的神经元按照一定的层次结构连接起来,就得到了神经网络。
2 神经网络的种类
2.1 单层神经网络
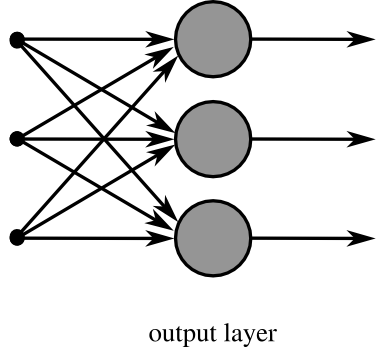
单层神经网络是最基本的神经元网络形式,由有限个神经元构成,所有神经元的输入向量都是同一个向量。由于每一个神经元都会产生一个标量结果,所以单层神经元的输出是一个向量,向量的维数等于神经元的数目。
示意图如下:
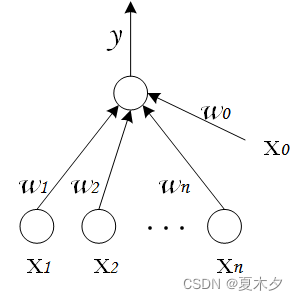
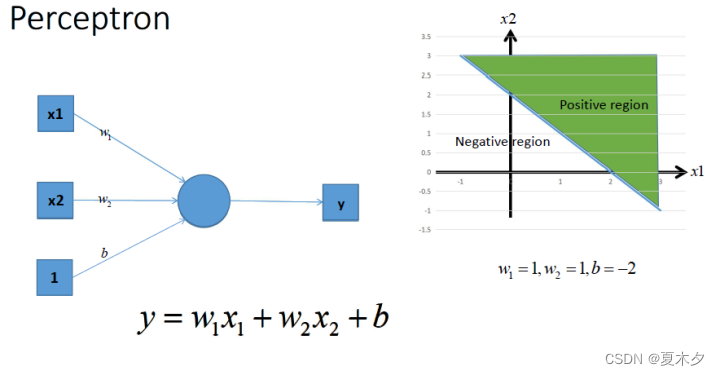
2.2 感知机
感知机由两层神经网络组成,输入层接收外界输入信号后传递给输出层(输出+1正例,-1反例),输出层是 M-P 神经元。
感知机的作用:
把一个n维向量空间用一个超平面分割成两部分,给定一个输入向量,超平面可以判断出这个向量位于超平面的哪一边,得到输入时正类或者是反类,对应到2维空间就是一条直线把一个平面分为两个部分。(简单的二分类模型,给定阈值,判断数据属于哪一部分)
超平面:是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中,一条直线是一维的,它把平面分成了两块;三维空间中,一个平面是二维的,它把空间分成了两块
2.3 多层神经网络
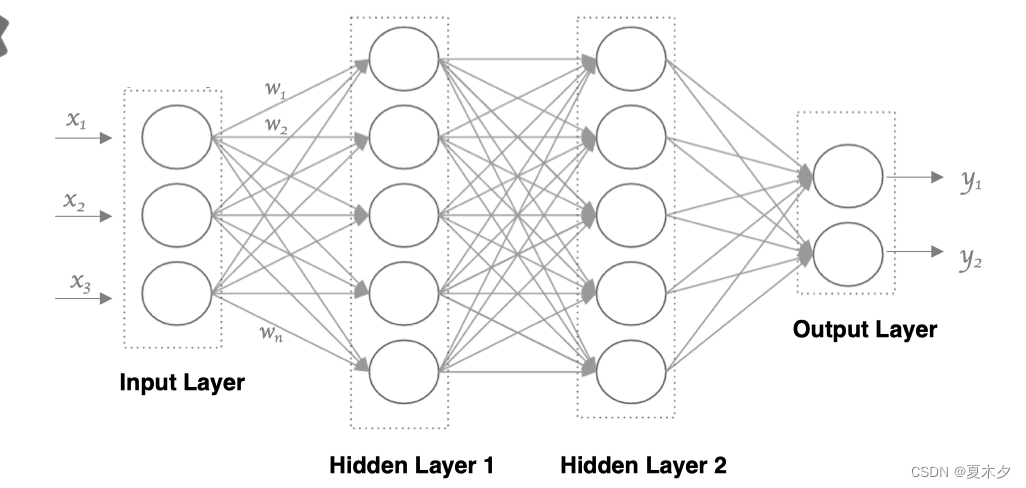
多层神经网络就是由单层神经网络进行叠加之后得到的,所以就形成了 层 的概念,常见的多层神经网络有如下结构:
- 输入层(Input layer),众多神经元(Neuron)接受大量输入消息。输入的消息称为输入向量。
- 输出层(Output layer),消息在神经元链接中传输、分析、权衡,形成输出结果。输出的消息称为输出向量。
- 隐藏层(Hidden layer),简称“隐层”,是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有一层或多层。隐层的节点(神经元)数目不定,但数目越多神经网络的非线性越显著,从而神经网络的强健性(robustness)更显著。
利用神经元来构建神经网络,相邻层之间的神经元相互连接,并给每一个连接分配一个强度,如下图所示:
特点是:
- 神经网络中信息只向一个方向移动,即从输入节点向前移动,通过隐藏节点,再向输出节点移动,网络中没有循环或者环。
- 同一层的神经元之间没有连接
- 每个连接都有一个权值
- 第 N 层的每个神经元和第 N-1 层的所有神经元相连(这就是full connected的含义),第 N-1 层神经元的输出就是第 N 层神经元的输入
- 所谓的全连接层就是在前一层的输出的基础上进行一次 Y = W x + b Y=Wx+b Y=Wx+b的变化(不考虑激活函数的情况下就是一次线性变化,所谓线性变化就是平移(+b)和缩放的组合(*w))
3 神经元的工作方式
人工神经元接收到一个或多个输入,对他们进行加权并相加,总和通过一个非线性函数(激活函数)产生输出。
- 所有的输入xi,与相应的权重 wi 相乘并求和
- 将求和结果送入到激活函数中,得到最终的输出结果:
3.1 激活函数
激活函数的作用
在前面的神经元的介绍过程中我们提到了激活函数,那么它到底是干什么的呢?
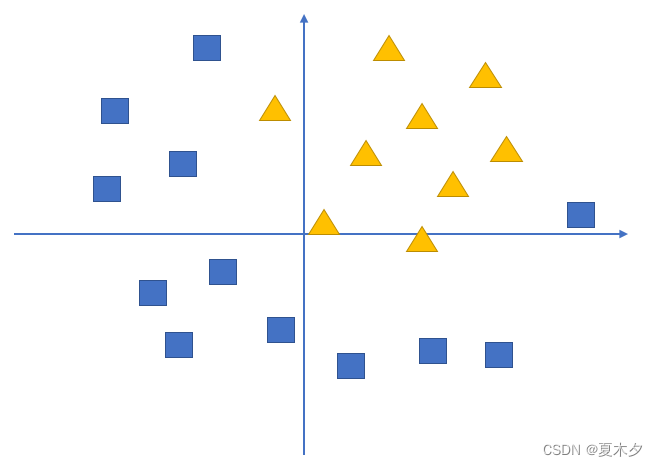
假设我们有这样一组数据,三角形和四边形,需要把他们分为两类
通过不带激活函数的感知机模型我们可以划出一条线, 把平面分割开
假设我们确定了参数 w 和 b 之后,那么带入需要预测的数据,如果 y>0,我们认为这个点在直线的右边,也就是正类(三角形),否则是在左边(四边形)
但是可以看出,三角形和四边形是没有办法通过直线分开的,那么这个时候该怎么办?
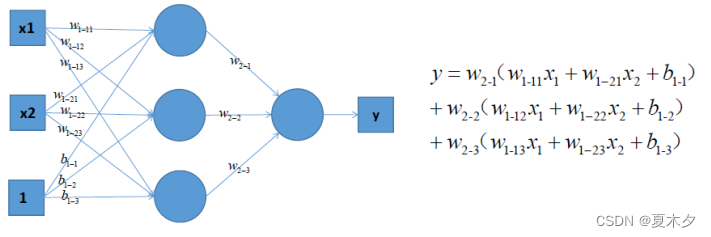
可以考虑使用多层神经网络来进行尝试,比如在前面的感知机模型中再增加一层,如下图:
对上图中的等式进行合并,我们可以得到:
y
=
(
w
1
−
11
w
2
−
1
+
⋯
)
x
1
+
(
w
1
−
21
w
2
−
1
+
⋯
)
x
2
+
(
w
2
−
1
+
⋯
)
b
1
−
1
y = (w_{1-11}w_{2-1}+\cdots)x_1+(w_{1-21}w_{2-1}+\cdots)x_2 + (w_{2-1}+\cdots)b_{1-1}
y=(w1−11w2−1+⋯)x1+(w1−21w2−1+⋯)x2+(w2−1+⋯)b1−1
上式括号中的都为w参数,和公式
y
=
w
1
x
1
+
w
2
x
2
+
b
y = w_1x_1 + w_2x_2 +b
y=w1x1+w2x2+b完全相同,依然只能够绘制出直线。但是可以发现,即使是多层神经网络,相比于前面的感知机,没有任何的改进。
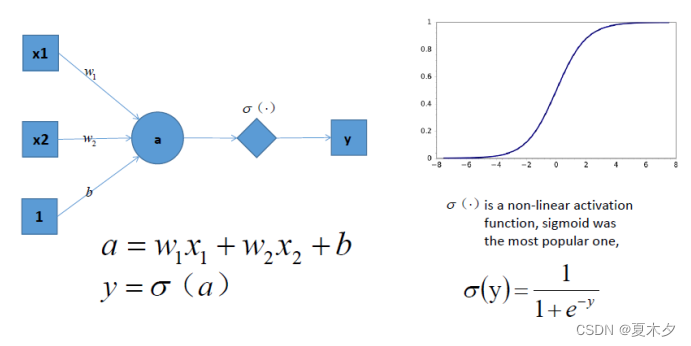
但是如果此时,我们在前面感知机的基础上加上非线性的激活函数之后,输出的结果就不在是一条直线
如上图,右边是 sigmoid 函数,对感知机的结果,通过 sigmoid 函数进行处理
如果给定合适的参数 w 和 b,就可以得到合适的曲线,能够完成对最开始问题的非线性分割
所以激活函数很重要的一个作用就是增加模型的非线性分割能力
在神经元中引入了 激活函数 ,它的本质是向神经网络中引入 非线性因素的,通过激活函数,神经网络就可以拟合各种曲线。如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,引入非线性函数作为激活函数,那输出不再是输入的线性组合,可以逼近任意函数。
激活函数的种类
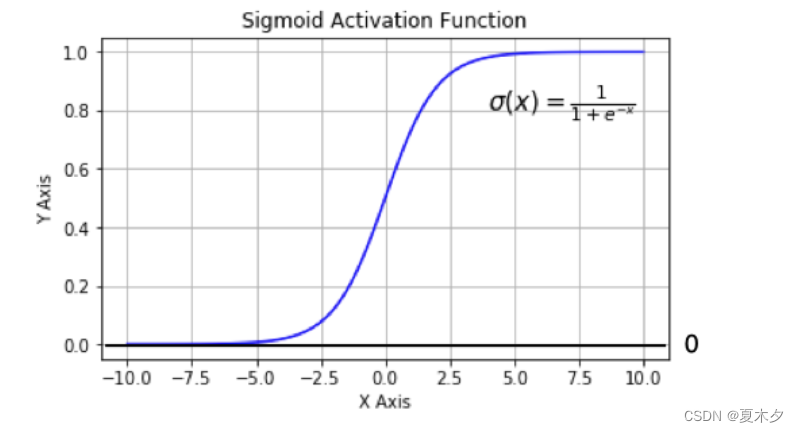
(1)Sigmoid / logistics 函数
数学表达式:
曲线图像:
sigmoid 在定义域内处处可导,且两侧导数逐渐趋近于0。如果X的值很大或者很小的时候,那么函数的梯度(函数的斜率)会非常小,在反向传播的过程中,导致了向低层传递的梯度也变得非常小。此时,网络参数很难得到有效训练。这种现象被称为 梯度消失 。
一般来说, sigmoid 网络在 5 层之内就会产生梯度消失现象。而且,该激活函数并不是以 0 为中心的(是以 0.5 为中心的),所以在实践中这种激活函数使用的很少。
sigmoid函数一般只用于 二分类 的输出层。
实现方法:
# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 定义x的取值范围
x = np.linspace(-10, 10, 100)
# 直接使用tensorflow实现
y = tf.nn.sigmoid(x)
# 绘图
plt.plot(x,y)
plt.grid()
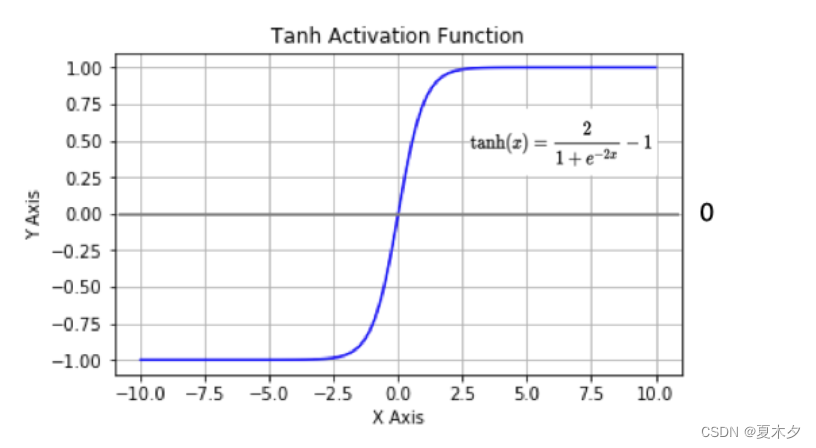
(2)tanh(双曲正切曲线)
数学表达式:
曲线图像:
tanh 也是一种非常常见的激活函数。与 sigmoid 相比,它是以 0 为中心的,使得其收敛速度要比 sigmoid 快(相比之下,tanh 曲线更为陡峭一些),减少迭代次数。然而,从图中可以看出,tanh 两侧的导数也为 0,同样会造成梯度消失。
若使用时可在隐藏层使用 tanh 函数,在输出层使用 sigmoid 函数。
实现方法:
# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 定义x的取值范围
x = np.linspace(-10, 10, 100)
# 直接使用tensorflow实现
y = tf.nn.tanh(x)
# 绘图
plt.plot(x,y)
plt.grid()
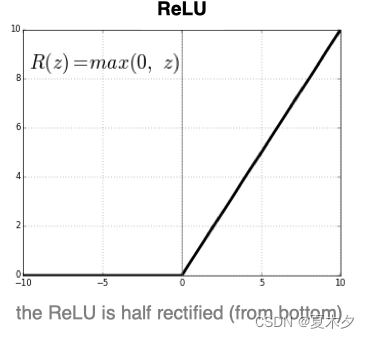
(3)RELU
数学表达式为:
曲线如下图所示:
ReLU是目前最常用的激活函数。 从图中可以看到,当x<0时,ReLU导数为0,而当x>0时,则不存在饱和问题。所以,ReLU 能够在x>0时保持梯度不衰减,从而缓解梯度消失问题。然而,随着训练的推进,部分输入会落入小于0区域,导致对应权重无法更新。这种现象被称为“神经元死亡”。
Relu是输入只能大于0,如果你输入含有负数,Relu就不适合,如果你的输入是图片格式,Relu就挺常用的,因为图片的像素值作为输入时取值为[0,255]。
与sigmoid相比,RELU的优势是:
- 采用sigmoid函数,计算量大(指数运算),反向传播求误差梯度时,求导涉及除法,计算量相对大,而采用Relu激活函数,整个过程的计算量节省很多。
- sigmoid函数反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
- Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
实现方法为:
# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 定义x的取值范围
x = np.linspace(-10, 10, 100)
# 直接使用tensorflow实现
y = tf.nn.relu(x)
# 绘图
plt.plot(x,y)
plt.grid()
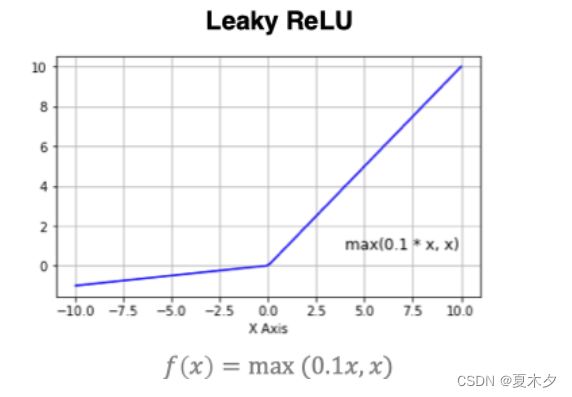
(4)LeakyReLu
该激活函数是对RELU的改进,数学表达式为:
曲线如下所示:
实现方法为:
# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 定义x的取值范围
x = np.linspace(-10, 10, 100)
# 直接使用tensorflow实现
y = tf.nn.leaky_relu(x)
# 绘图
plt.plot(x,y)
plt.grid()
(5)SoftMax
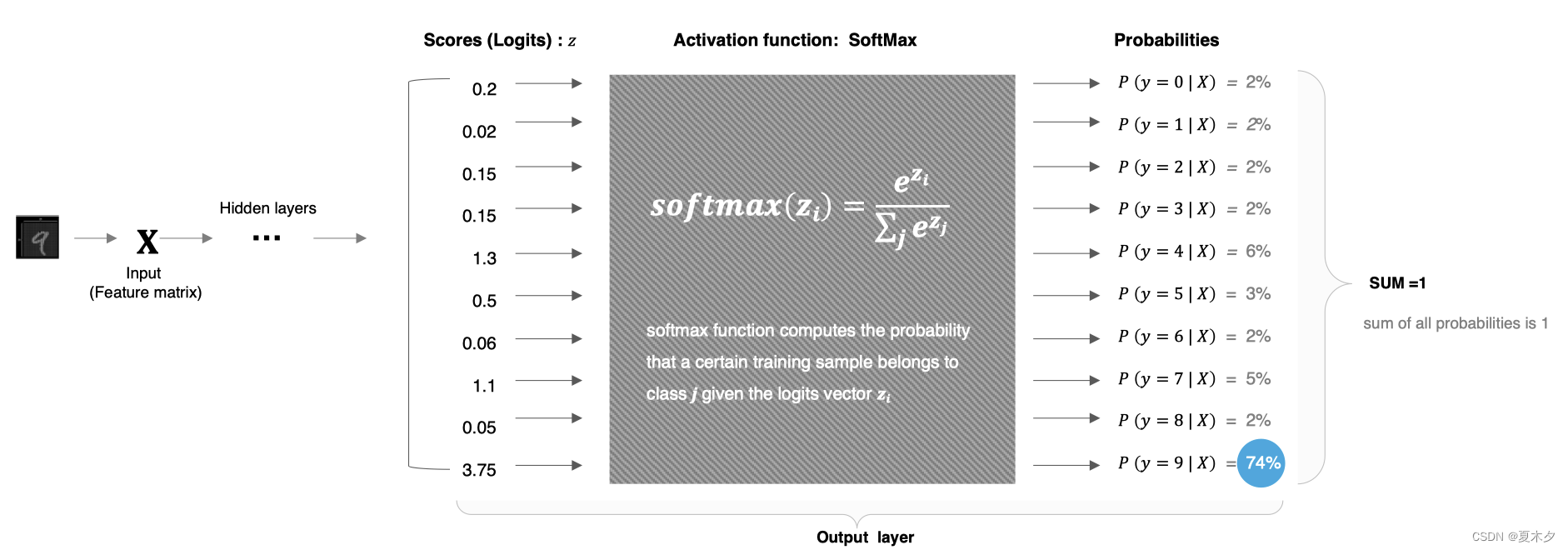
softmax用于多分类过程中,它是二分类函数 sigmoid 在多分类上的推广,目的是将多分类的结果以概率的形式展现出来。
数学表达式为:
使用方法:
softmax 直白来说就是将网络输出的 logits 通过softmax函数,就映射成为(0,1)的值,而这些值的累和为1(满足概率的性质),那么我们将它理解成概率,选取概率最大(也就是值对应最大的)接点,作为我们的预测目标类别。
实现方法:
# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 数字中的score
x = tf.constant([0.2,0.02,0.15,0.15,1.3,0.5,0.06,1.1,0.05,3.75])
# 将其送入到softmax中计算分类结果
y = tf.nn.softmax(x)
# 将结果进行打印
print(y)
分类结果为:
tf.Tensor(
[0.0212338 0.01773596 0.02019821 0.02019821 0.06378984 0.02866262
0.01845977 0.0522267 0.0182761 0.73921883], shape=(10,), dtype=float32)
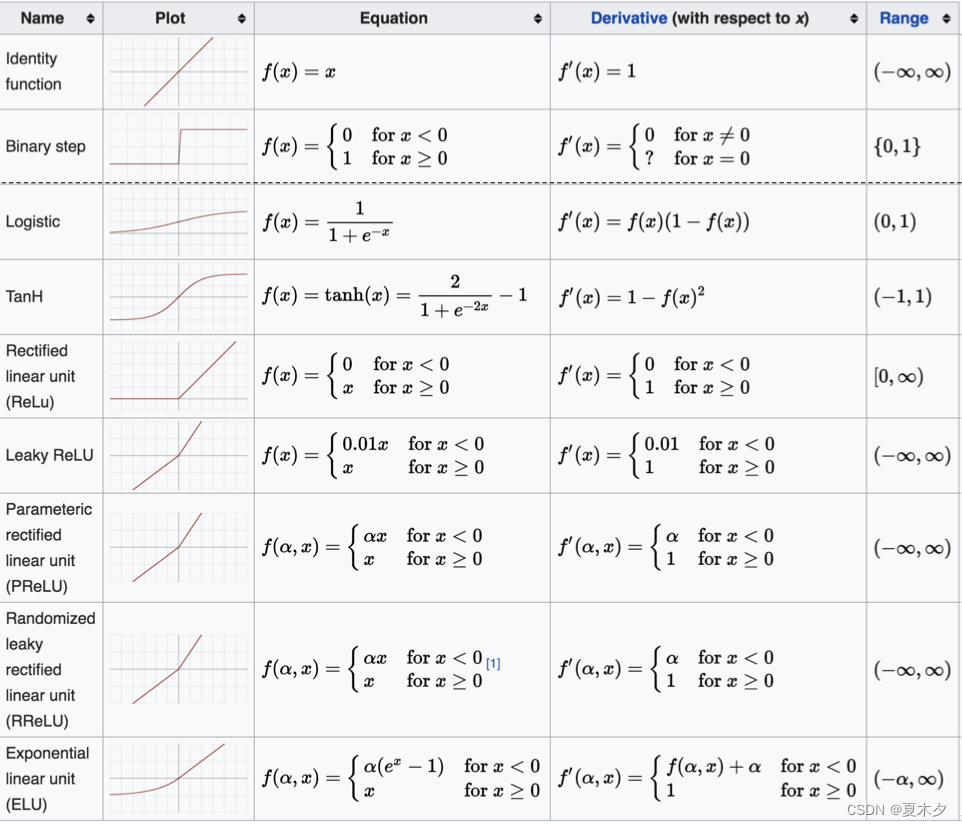
(6)其他激活函数
如何选择激活函数?
- 隐藏层
- 优先选择RELU激活函数
- 如果ReLu效果不好,那么尝试其他激活,如Leaky ReLu等。
- 如果你使用了Relu, 需要注意一下Dead Relu问题, 避免出现大的梯度从而导致过多的神经元死亡。
- 不要使用sigmoid激活函数,可以尝试使用tanh激活函数
- 输出层
- 二分类问题选择sigmoid激活函数
- 多分类问题选择softmax激活函数
- 回归问题选择identity激活函数
激活函数的作用除了前面说的增加模型的非线性分割能力外,还有
- 提高模型鲁棒性
- 缓解梯度消失问题
- 加速模型收敛等
3.2 参数初始化
对于某一个神经元来说,需要初始化的参数有两类:一类是权重W,还有一类是偏置b,偏置b初始化为0即可。而权重W的初始化比较重要,我们着重来介绍常见的初始化方式。
(1)随机初始化
随机初始化从均值为 0,标准差是 1 的高斯分布(也叫正态分布)中取样,使用一些很小的值对参数 W 进行初始化。
(2)标准初始化
权重参数初始化从区间均匀随机取值。即在(-1/√d,1/√d)均匀分布中生成当前神经元的权重,其中 d 为每个神经元的输入数量。
(3)Xavier 初始化(在 tf.keras 中 默认 使用)
该方法的基本思想是各层的激活值和梯度的方差在传播过程中保持一致,也叫做 Glorot 初始化。在tf.keras中实现的方法有两种:
① 正态化的 Xavier 初始化
Glorot 正态分布初始化器,也称为 Xavier 正态分布初始化器。它从以 0 为中心,标准差为 stddev = sqrt(2 / (fan_in + fan_out)) 的正态分布中抽取样本, 其中 fan_in 是输入神经元的个数, fan_out 是输出的神经元个数。
实现方法为:
# 导入工具包
import tensorflow as tf
# 进行实例化
initializer = tf.keras.initializers.glorot_normal()
# 采样得到权重值
values = initializer(shape=(9, 1))
# 打印结果
print(values)
输出的结果为:
tf.Tensor(
[[ 0.71967787]
[ 0.56188506]
[-0.7327265 ]
[-0.05581591]
[-0.05519835]
[ 0.11283273]
[ 0.8377778 ]
[ 0.5832906 ]
[ 0.10221979]], shape=(9, 1), dtype=float32)
② 标准化的 Xavier 初始化
Glorot 均匀分布初始化器,也称为 Xavier 均匀分布初始化器。它从 [-limit,limit] 中的均匀分布中抽取样本, 其中 limit 是 sqrt(6 / (fan_in + fan_out)), 其中 fan_in 是输入神经元的个数, fan_out 是输出的神经元个数。
# 导入工具包
import tensorflow as tf
# 进行实例化
initializer = tf.keras.initializers.glorot_uniform()
# 采样得到权重值
values = initializer(shape=(9, 1))
# 打印结果
print(values)
输出结果为:
tf.Tensor(
[[-0.59119344]
[ 0.06239486]
[ 0.65161395]
[-0.30347362]
[-0.5407096 ]
[ 0.35138106]
[ 0.41150713]
[ 0.32143414]
[-0.57354397]], shape=(9, 1), dtype=float32)
(4)He 初始化
he初始化,也称为Kaiming初始化,出自大神何恺明之手,它的基本思想是正向传播时,激活值的方差保持不变;反向传播时,关于状态值的梯度的方差保持不变。在tf.keras中也有两种:
① 正态化的 He 初始化
He 正态分布初始化是以 0 为中心,标准差为 stddev = sqrt(2 / fan_in) 的截断正态分布中抽取样本, 其中 fan_in 是输入神经元的个数,在tf.keras中的实现方法为:
# 导入工具包
import tensorflow as tf
# 进行实例化
initializer = tf.keras.initializers.he_normal()
# 采样得到权重值
values = initializer(shape=(9, 1))
# 打印结果
print(values)
输出结果为:
tf.Tensor(
[[-0.1488019 ]
[-0.12102155]
[-0.0163257 ]
[-0.36920077]
[-0.89464396]
[-0.28749225]
[-0.5467023 ]
[ 0.27031776]
[-0.1831588 ]], shape=(9, 1), dtype=float32)
② 标准化的 He 初始化
He 均匀方差缩放初始化器。它从 [-limit,limit] 中的均匀分布中抽取样本, 其中 limit 是 sqrt(6 / fan_in), 其中 fan_in 输入神经元的个数。实现为:
# 导入工具包
import tensorflow as tf
# 进行实例化
initializer = tf.keras.initializers.he_uniform()
# 采样得到权重值
values = initializer(shape=(9, 1))
# 打印结果
print(values)
输出结果为:
tf.Tensor(
[[ 0.80033934]
[-0.18773115]
[ 0.6726284 ]
[-0.23672342]
[-0.6323329 ]
[ 0.6048162 ]
[ 0.1637358 ]
[ 0.60797024]
[-0.46316862]], shape=(9, 1), dtype=float32)
4 神经网络的搭建
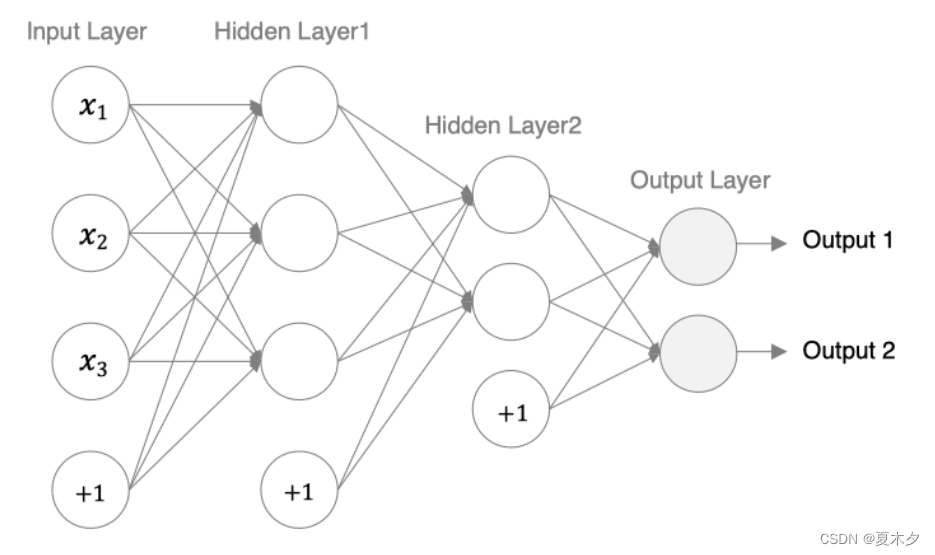
接下来我们来构建如下图所示的神经网络模型:
tf.Keras 中构建模有两种方式,一种是通过 Sequential 构建,一种是通过 Model 类构建。前者是按一定的顺序对层进行堆叠,而后者可以用来构建较复杂的网络模型。首先我们介绍下用来构建网络的全连接层:
tf.keras.layers.Dense(
units, activation=None, use_bias=True, kernel_initializer='glorot_uniform',
bias_initializer='zeros')
主要参数:
units: 当前层中包含的神经元个数Activation: 激活函数,relu,sigmoid等use_bias: 是否使用偏置,默认使用偏置Kernel_initializer: 权重的初始化方式,默认是Xavier初始化bias_initializer: 偏置的初始化方式,默认为0
4.1 通过Sequential构建
Sequential() 提供一个层的列表,就能快速地建立一个神经网络模型,实现方法如下所示:
# 导入相关的工具包
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
# 定义一个Sequential模型,包含3层
model = keras.Sequential(
[
# 第一层(隐藏层):激活函数为relu,权重初始化为he_normal
layers.Dense(3, activation="relu",
kernel_initializer="he_normal", name="layer1",input_shape=(3,)),
# 第二层(隐藏层):激活函数为relu,权重初始化为he_normal
layers.Dense(2, activation="relu",
kernel_initializer="he_normal", name="layer2"),
# 第三层(输出层):激活函数为sigmoid,权重初始化为he_normal
layers.Dense(2, activation="sigmoid",
kernel_initializer="he_normal", name="layer3"),
],
name="my_Sequential" # 定义该模型的名字
)
展示模型结果:
# 展示模型结果
model.summary()
如下所示:
Model: "my_Sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
layer1 (Dense) (None, 3) 12
_________________________________________________________________
layer2 (Dense) (None, 2) 8
_________________________________________________________________
layer3 (Dense) (None, 2) 6
=================================================================
Total params: 26
Trainable params: 26
Non-trainable params: 0
_________________________________________________________________
通过这种 sequential 的方式只能构建简单的序列模型,较复杂的模型没有办法实现。
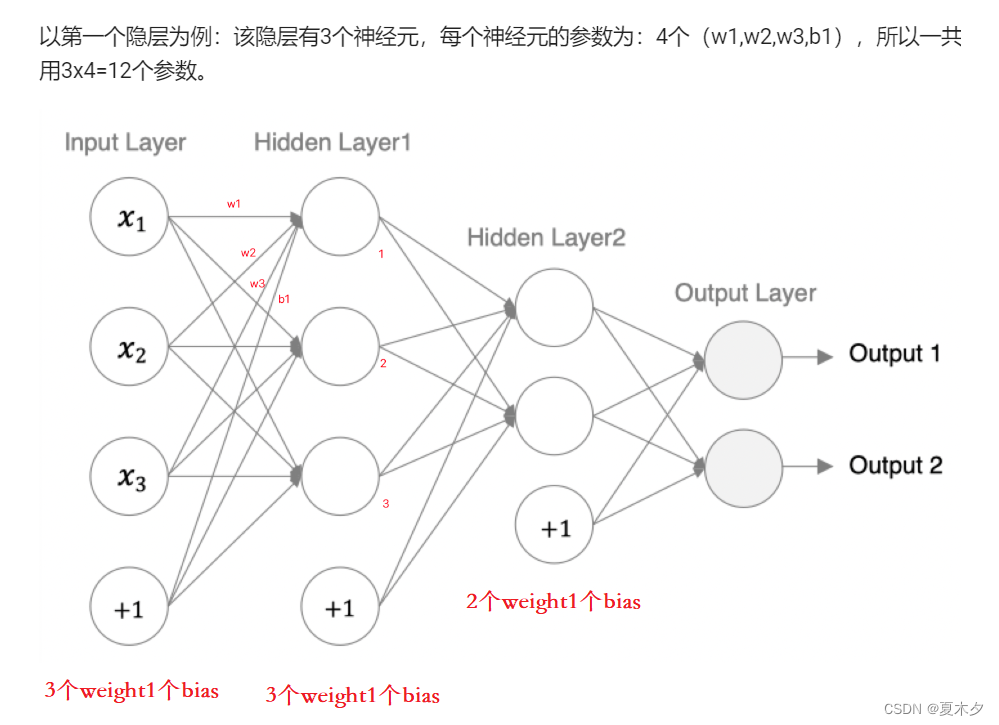
拓展:参数个数的计算
4.2 利用function API构建
tf.keras 提供了 Functional API,建立更为复杂的模型,使用方法是将层作为可调用的对象并返回张量,并将输入向量和输出向量提供给 tf.keras.Model 的 inputs 和 outputs 参数,实现方法如下:
# 导入工具包
import tensorflow as tf
# 定义模型的输入
inputs = tf.keras.Input(shape=(3,),name = "input")
# 第一层:激活函数为relu,其他默认
x = tf.keras.layers.Dense(3, activation="relu",name = "layer1")(inputs)
# 第二层:激活函数为relu,其他默认
x = tf.keras.layers.Dense(2, activation="relu",name = "layer2")(x)
# 第三层(输出层):激活函数为sigmoid
outputs = tf.keras.layers.Dense(2, activation="sigmoid",name = "layer3")(x)
# 使用Model来创建模型,指明输入和输出
model = tf.keras.Model(inputs=inputs, outputs=outputs,name="my_model")
展示模型结果:
model.summary()
或者
# 模型展示
keras.utils.plot_model(model,show_shapes=True)
4.3 通过model的子类构建
通过 model 的子类构建模型,此时需要在 __init__ 中定义神经网络的层,在 call 方法中定义网络的前向传播过程,实现方法如下:
# 导入工具包
import tensorflow as tf
# 定义model的子类
class MyModel(tf.keras.Model):
# 在init方法中定义网络的层结构
def __init__(self):
super(MyModel, self).__init__()
# 第一层:激活函数为relu,权重初始化为he_normal
self.layer1 = tf.keras.layers.Dense(3, activation="relu",
kernel_initializer="he_normal", name="layer1",input_shape=(3,))
# 第二层:激活函数为relu,权重初始化为he_normal
self.layer2 =tf.keras.layers.Dense(2, activation="relu",
kernel_initializer="he_normal", name="layer2")
# 第三层(输出层):激活函数为sigmoid,权重初始化为he_normal
self.layer3 =tf.keras.layers.Dense(2, activation="sigmoid",
kernel_initializer="he_normal", name="layer3")
# 在call方法中完成前向传播
def call(self, inputs):
x = self.layer1(inputs)
x = self.layer2(x)
return self.layer3(x)
# 实例化模型
model = MyModel()
# 设置一个输入,调用模型(否则无法使用summay())
x = tf.ones((1, 3))
y = model(x)
展示模型结果:
model.summary()
此时就不能使用
keras.utils.plot_model(model,show_shapes=True)展示模型架构了
5 小结
神经网络的优缺点:
- 优点
- 精度高,性能优于其他的机器学习方法,甚至在某些领域超过了人类
- 可以近似任意的非线性函数
- 随之计算机硬件的发展,近年来在学界和业界受到了热捧,有大量的框架和库可供调用
- 缺点
- 黑箱,很难解释模型是怎么工作的
- 训练时间长,需要大量的计算力
- 网络结构复杂,需要调整超参数
- 小数据集上表现不佳,容易发生过拟合