【题目描述】
在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并,多多可以把其中任意不超过k堆果子合并到一起,消耗的体力等于合并在一起的这些堆果子的重量之和。最终合并成为一堆果子。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。
例如有5堆果子,数目依次为3,2,1,4,5,每次合并最多3堆。可以先将1、2、3堆合并,新堆数目为6,耗费体力为6。接着,将新堆与剩下的两堆合并,又得到新的堆,数目为15,耗费体力为15。所以多多总共耗费体力=6+15=21。可以证明21为最小的体力耗费值。
【输入】
输入包括两行,第一行是两个整数n和k(1<=n,k<=10000),表示果子的种类数和每次最多可以合并的堆数。第二行包含n个整数,用空格分隔,第i个整数ai(1<=ai<=20000)是第i种果子的数目。
【输出】
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。输入数据保证这个值小于
2
31
2^{31}
231
【数据规模】
对于30%的数据,保证有n<=1000:
对于50%的数据,保证有n<=5000;
对于全部的数据,保证有n<=10000。
【题解】
看到这道题,我就想起了标准的合并果子问题(一次合并2堆的那个),我想,一次合并K堆不得了呗!不足K堆时就把全部都合并掉!
结果我就WA(wrong answer)了,很明显,这不是正解!
首先,我们会发现,这道题目中最佳的合并方案就是每次合并最小的那几堆果子。
so,我们就要用小根堆来储存了。
那么,什么是小根堆呢? 戳这里☞☞☞ 给我看明白了!不然就看不懂下面的文字了!!!
然后每次删除堆顶元素,把它们的和算出来,用变量SUM储存,再把元素SUM插入堆中。
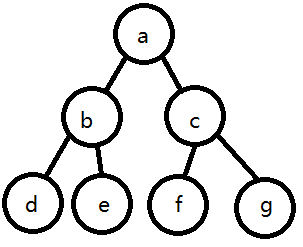
但问题是,每次合并K堆的做法是有问题的,如下图:
其中N=7,K=5.
设在这个小根堆中,a < b < c < d < e < f < g,用每次合并K堆,最后合并剩余的那几堆的方法,所用的体力值为:
2(a+b+c+d+e)+f+g
但很明显,这样做是错的。我们应该先合并3堆,再合并5堆,即所用的体力值为
2(a+b+c)+d+e+f+g
所以我们第一次合并的次数不一定是K,但后面每一次合并的次数一定是K!
通过找规律,我发现第一次合并的次数是
如果 ( k − 1 ) ∣ ( n − 1 ) (k-1)\mid(n-1) (k−1)∣(n−1),第一次合并k次
如果 ( k − 1 ) ∣ ̸ ( n − 1 ) {(k-1)\space|\not \space(n-1)} (k−1) ∣ (n−1),第一次合并 ( n − 1 ) m o d ( k − 1 ) {(n-1)mod(k-1)} (n−1)mod(k−1)次
然后就可以了。
下面附上标程——
#include<cstdio>
using namespace std;
int a[10010],num;
void up(int x)
{
int t;
while(x>1&&a[x]<a[x/2])
{
t=a[x];
a[x]=a[x/2];
a[x/2]=t;
x=x/2;
}
}
void down(int x)
{
int t;
while(x*2<=num&&(a[x]>a[x*2]||a[x]>a[x*2+1]))
{
if(a[x*2+1]>a[x*2]||x*2+1>num)
{
t=a[x];a[x]=a[x*2];a[x*2]=t;
x=x*2;
}
else
{
t=a[x];a[x]=a[x*2+1];a[x*2+1]=t;
x=x*2+1;
}
}
}
void inc(int x)
{
a[++num]=x;
up(num);
}
void del(int x)
{
a[x]=a[num];
num--;down(x);
}
int main()
{
freopen("fruit.in","r",stdin);
freopen("fruit.out","w",stdout);
int n,i,j,k,ans=0,t,l;
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++)
{
scanf("%d",&j);
inc(j);
}
if((n-1)%(k-1)==0) l=k;
else l=(n-1)%(k-1)+1;
while(num>1)
{
t=0;
for(i=1;i<=l;i++)
{
t=t+a[1];
ans=ans+a[1];
if(num==0) break;
del(1);
}
inc(t);
l=k;
}
printf("%d\n",ans);
return 0;
}