leetCode刷题记录3-面试经典150题

文章目录

不要摆，没事干就刷题，只有好处，没有坏处，实在不行，看看竞赛题
- 面试经典 150 题

不要摆，没事干就刷题，只有好处，没有坏处，实在不行，看看竞赛题

面试经典 150 题

80. 删除有序数组中的重复项 II

public int removeDuplicates(int[] nums) {
    int k = 0, count = 1;
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] != nums[k]) {
            nums[++k] = nums[i];
            count = 1;
        } else if (++count <= 2) {
            nums[++k] = nums[i];
        }
    }
    return k + 1;
}

189. 轮转数组

408原题，4刷了，现在感觉很水了

注意k可能很大，需要对长度取一下模

public void rotate(int[] nums, int k) {
    int n = nums.length-1;
    k = k%(n+1);
    reverse(nums,0,n-k);
    reverse(nums,n-k+1,n);
    reverse(nums,0,n);
}

public void reverse(int[] nums, int l,int r) {
    while (l<r){
        int t = nums[l];
        nums[l] = nums[r];
        nums[r] = t;
        l++;r--;
    }
}

122. 买卖股票的最佳时机 II

没啥头绪，先暴力拿分，也是能力

DFS暴力枚举，过了198个，也不错了
剩下两个超时

public int maxProfit(int[] prices) {
    dfs(prices,-1,0,0);
    return max;
}

int max = -1;
public int dfs(int[] prices,int curr,int index,int sum){
    //System.out.println(index+" "+sum);
    max = Math.max(max,sum);
    if(index>=prices.length) return 0;

    if(curr!=-1){//当前持有股票
        // 不卖
        dfs(prices,curr,index+1,sum);
        // 卖
        if(prices[index]>curr) dfs(prices,-1,index+1,sum+prices[index]);
    }else {//当前无股票
        // 买
        dfs(prices,prices[index],index+1,sum-prices[index]);
        // 不买
        dfs(prices,-1,index+1,sum);
    }
    return 0;
}

先自己优化时间
强制加缓存，竟然超出内存限制

public int maxProfit(int[] prices) {
    return dfs(prices,-1,0);
}
HashMap<String, Integer> cache = new HashMap<>();
public int dfs(int[] prices,int curr,int index){
    //System.out.println(index+" "+sum);
    if(index>=prices.length) return 0;
    String key = ""+curr+"-"+index;
    if(cache.get(key)!=null) return cache.get(key);
    int ans = 0;
    if(curr!=-1){//当前持有股票
        // 不卖
        int t1 = dfs(prices,curr,index+1);
        int t2=0;
        // 卖 sum+prices[index]
        if(prices[index]>curr) {
            t2 = dfs(prices,-1,index+1)+prices[index];
        }
        ans = Math.max(t1,t2);
    }else {//当前无股票
        // 买 sum-prices[index]
        int t1 = -prices[index]+dfs(prices,prices[index],index+1);
        // 不买 sum
        int t2 = dfs(prices,-1,index+1);
        ans = Math.max(t1,t2);
    }
    cache.put(key,ans);
    return ans;
}

在这里插入图片描述
没办法，看题解喽

看题解后我傻了，这一题竟然可以直接贪心

public int maxProfit(int[] prices) {
    int ans = 0;
    for (int i = 1; i < prices.length; i++) {
        int  p = prices[i]-prices[i-1];
        if(p>0) ans+=p;
    }
    return ans;
}

dp也很简单，但是自己的猪脑想不到，不会分析

// 也很简单 持有股票和没有股票两种状态而已 0不持有  1持有
public int maxProfit(int[] prices) {
    int n = prices.length;
    int[][] dp = new int[n][2];
    dp[0][1] = -prices[0];
    for (int i = 1; i < prices.length; i++) {
        dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);//[头一天不持有股票且今天不买][头一天持有股票今天卖了]
        dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);//[头一天就持有股票且今天不卖][头一天不持有股票且今天买了]
    }
    return dp[n-1][0];
}

55. 跳跃游戏

这一题直接暴力(也才O(n))肯定能想出最优解

// 就是简单爆力也才O(n)呀 所以遇到题目先想暴力解法 很有帮助
public boolean canJump(int[] nums) {
    int n = nums.length;
    int max = nums[0];
    for (int i = 1; i < nums.length; i++) {
        if(i>max) return false;
        max = Math.max(max,i+nums[i]);
        if(max>=n-1) return true;
    }
    return max>=n-1;
}

45. 跳跃游戏 II

有了上一题作为坑，这一题很快就过了

public int jump(int[] nums) {
    int n = nums.length;
    int[] dp = new int[n];
    Arrays.fill(dp,n);
    dp[0]=0;

    for (int i = 0; i < n; i++) {
        for (int j = 1; j <= nums[i]; j++) {
            int k = i+j;
            if(i+j<n) dp[k] = Math.min(dp[k], dp[i]+1);
        }
    }
    //print(dp);
    return dp[n-1];//到达不了时就大于n
}

但是时间比较慢
在这里插入图片描述
看题解优化：

果然还是有很简单的思路，但是自己就是整理不出来
在这里插入图片描述

public int jump(int[] nums) {
   int n = nums.length;
   if(n==1) return 0;

   int step=0;
   int start = 0;
   int end = 1;

   while (end<n){

       int max = 0;//只维护这个区间最大
       for (int i = start; i < end; i++) {
           max = Math.max(max,nums[i]+i);
       }
       start = end;
       end = max+1;
       step++;
   }
   return step;
}

380. O(1) 时间插入、删除和获取随机元素

先暴力拿分，就是HashSet

class RandomizedSet {

    HashSet<Integer> set = new HashSet<>();

    public RandomizedSet() {

    }

    public boolean insert(int val) {
        return set.add(val);
    }

    public boolean remove(int val) {
        return set.remove(val);
    }

    public int getRandom() {
        return new ArrayList<Integer>(set).get(new Random().nextInt(set.size()));
    }
}

看了题解才明白，本题就是让你用HashMap实现HashSet
具体： HashMap+List 实现本题的数据结构

核心： HashMap不仅记录是否存在还记录下标不存在为null

错误： list.remove(hash.get(val));//这是O(n) 因为会把后面元素前移得换策略

class RandomizedSet {

    HashMap<Integer, Integer> hash = new HashMap<>();//HashMap不仅记录是否存在 还记录下标 不存在为null
    ArrayList<Integer> list = new ArrayList<>();
    Random random = new Random();

    public RandomizedSet() {
    }

    public boolean insert(int val) {
        if(hash.containsKey(val)){
            return false;
        }else {
            list.add(val);
            hash.put(val,list.size()-1);
            return true;
        }
    }

    public boolean remove(int val) {
        if(!hash.containsKey(val)){
            return false;
        }else {
            list.remove(hash.get(val));//这是O(n) 得换策略
            hash.remove(val);
            return true;
        }
    }

    public int getRandom() {
        return list.get(random.nextInt(list.size()));
    }
}

真的O(1)

class RandomizedSet {

    public HashMap<Integer, Integer> hash = new HashMap<>();//HashMap不仅记录是否存在 还记录下标 不存在为null
    public ArrayList<Integer> list = new ArrayList<>();
    Random random = new Random();

    public RandomizedSet() {
    }

    public boolean insert(int val) {
        if (hash.containsKey(val)) {
            return false;
        } else {
            list.add(val);
            hash.put(val, list.size() - 1);
            return true;
        }
    }

    public boolean remove(int val) {
        if (!hash.containsKey(val)) {
            return false;
        } else {
            int i = hash.get(val);
            int n = list.size() - 1;
            list.set(i, list.get(n));
            hash.put(list.get(n),i);//一定要更新最后一个元素的下标呀  ！！！！！
            list.remove(n);
            hash.remove(val);
            return true;
        }
    }

    public int getRandom() {
        return list.get(random.nextInt(list.size()));
    }
}

注意删除策略：最后一个元素替换被删除元素，再删除最后一个元素，也只有这样才是O(1),也只有这样才能更新最后一个元素的下标，也即保证删除后，所有元素下标hash表还是正确的。（移动后面元素下标都要-1）

134. 加油站

先暴力，果然超时

public int canCompleteCircuit(int[] gas, int[] cost) {
    int[] gc = new int[gas.length];
    ArrayList<Integer> indices= new ArrayList<>();
    for (int i = 0; i < gas.length; i++) {
        //print(gas[i]-cost[i]," ");
        gc[i] = gas[i]-cost[i];
        if(gc[i]>=0) indices.add(i);
    }

    Collections.sort(indices,((o1, o2) -> o2-o1));
    for (Integer i : indices) {
        int sum = gc[i];
        int j = (i+1)%gas.length;
        while (j!=i){
            sum += gc[j];
            if (sum < 0) break;
            j = (j+1)%gas.length;
        }
        if(j==i) return i;
    }
    return -1;
}

仔细一看，其实每次不需要从i+1继续遍历尝试，因为i开始能走到j-1，走不到j那么(i~j-1)开始必然都走不到j的，因为从i开始能走到中间某个位置剩余油量只会>=0

public int canCompleteCircuit(int[] gas, int[] cost) {
    int n = gas.length;
    int[] gc = new int[n];
    for (int i = 0; i < n; i++) {
        //print(gas[i]-cost[i]," ");
        gc[i] = gas[i] - cost[i];
    }

    int minI = 0;
    while (minI < n) {
        int sum = 0, cnt = 0;//minI是起点  cnt是本轮走了几步
        while (cnt < n) {
            int j = (minI + cnt) % n;
            sum += gas[j] - cost[j];
            if (sum < 0) break;
            cnt++;
        }
        if (cnt == n) {//此时sum>=0一定成立  太巧了  顺便判断了是否能走通 cnt==n走了一圈了
            return minI;
        } else {
            minI += cnt + 1;//下一步开始走 这一步必须等救济 (中间minI~minI+cnt不用尝试了 肯定走不通最后一步)
        }
    }

    return -1;
}

最后看题解发现了一个非常牛的解法：

从头开始计算累积盈利或亏空。亏空最严重的一个点必须放在最后一步走，等着前面剩余的救助

public int canCompleteCircuit(int[] gas, int[] cost) {
    int minI=0;
    int min = Integer.MAX_VALUE;
    int n = gas.length;
    int sum = 0;

    for (int i = 0; i < gas.length; i++) {
        sum += gas[i]-cost[i];
        if(sum<min) {
            min = sum;
            minI = i;
        }
    }
    if(min>0) return 0;//都大于0 直接返回0  新样例
    return sum<0?-1:(minI+1)%gas.length;
}

135. 分发糖果

看起来困难，其实不难，正向遍历一次dp，反向遍历再一次dp即可

public int candy(int[] ratings) {
    int n = ratings.length;
    int[] dp = new int[n];
    dp[0] = 1;
    for (int i = 1; i < n; i++) {
        if (ratings[i] > ratings[i - 1]) dp[i] = dp[i - 1] + 1;
        else dp[i] = 1;
    }
    int ans = dp[n - 1];
    for (int i = n - 2; i >= 0; i--) {
        if (ratings[i] > ratings[i + 1]) dp[i] = Math.max(dp[i], dp[i + 1] + 1);
        ans += dp[i];
    }
    return ans;
}

13. 罗马数字转整数

我的做法：直接贪心匹配

public int romanToInt(String s) {
    int ans = 0;
    for (int i = 0; i < s.length(); i++) {
        char c1='*',c2='*';
        c1 = s.charAt(i);
        if(i+1<s.length()) c2 = s.charAt(i+1);
        if(convert(""+c1+c2)!=-1){
            ans += convert(""+c1+c2);
            i++;
        }else {
            ans += convert(""+c1);
        }
    }
    return ans;
}

int convert(String s){
    int ans = -1;

    if(s.equals("IV")) ans = 4;
    else if (s.equals("IX")) ans = 9;
    else if (s.equals("XL")) ans = 40;
    else if (s.equals("XC")) ans = 90;
    else if (s.equals("CD")) ans = 400;
    else if (s.equals("CM")) ans = 900;
    else if (s.equals("I")) ans = 1;
    else if (s.equals("V")) ans = 5;
    else if (s.equals("X")) ans = 10;
    else if (s.equals("L")) ans = 50;
    else if (s.equals("C")) ans = 100;
    else if (s.equals("D")) ans = 500;
    else if (s.equals("M")) ans = 1000;

    return ans;
}

题解做法：发现规律，左<右时减去左，否则加上左，最后一个一定是+

public int romanToInt(String s) {
    int ans = 0;
    int pre = convert(s.charAt(0)); //pre>=cur 正常   pre<cur 减
    for (int i = 1; i < s.length(); i++) {
        int cur = convert(s.charAt(i));
        if (pre >= cur) ans += pre;
        else ans -= pre;
        pre = cur;
    }
    ans += pre;//最后一个一定是正的
    return ans;
}

int convert(char c) {
    int ans = -1;
    if (c == 'I') ans = 1;
    else if (c == 'V') ans = 5;
    else if (c == 'X') ans = 10;
    else if (c == 'L') ans = 50;
    else if (c == 'C') ans = 100;
    else if (c == 'D') ans = 500;
    else if (c == 'M') ans = 1000;
    return ans;
}

12. 整数转罗马数字

上一题反过来，感觉还要简单一点，直接贪心减就OK了

1 <= num <= 3999 数的范围很小，不会吧不会吧，不会真的有人打表吧

public String intToRoman(int num) {
    int[] val = {1000,900,500,400,100,90,50,40,10,9,5,4,1};
    String[] sign = {"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
    String ans ="";
    for (int i = 0; i < val.length; i++) {
        while (num>=val[i]){
            ans += sign[i];
            num -= val[i];
        }
    }
    return ans;
}

题解做法快多了
在这里插入图片描述

14. 最长公共前缀

直接暴力解题：完全靠测试数据Debug，感觉不是很好

// 直接比较吧
public String longestCommonPrefix(String[] strs) {
    int k = 0;
    if (strs.length == 0)  return "";
    if(strs.length==1) return strs[0];
    out:while (true){
        if(strs[0].length()==0) return "";
        for (int i = 1; i < strs.length; i++) {
            if(k>=strs[i].length()||k>=strs[0].length()||strs[i].charAt(k)!=strs[0].charAt(k)) break out;
        }
        k++;
    }
    return strs[0].substring(0,k);
}

我的做法相当于纵向比较，题解有个横向比较法，觉得不错：
初始化ans=strs[0]
然后1~n分别和ans比较，中途更新ans

// 直接比较吧
public String longestCommonPrefix(String[] strs) {
    if (strs.length == 0) return "";
    String ans = strs[0];
    for (int i = 1; i < strs.length; i++) {
        int j = 0;
        for (; j < ans.length() && j < strs[i].length(); j++) {
            if(ans.charAt(j)!=strs[i].charAt(j)) break;
        }
        ans = ans.substring(0,j);
        if("".equals(ans)) return ans;
    }
    return ans;
}

6. N 字形变换

先暴力模拟，真的拿一个数组存一下

public String convert(String s, int m) {
    if(m==1) return s;

    int n = s.length();
    char[][] zArray = new char[m][n];//默认值 ''

    int i = 0, j = 0;
    int k = 0;
    int maxj = 0;
    boolean down = true;
    zArray[i][j] = s.charAt(k++);
    while (k < n) {
        if (down) {//直下
            if (i + 1 < m) {//可以往下
                i++;
            } else {//否则斜上走
                i--;
                j++;
                down = false;
            }
        } else {//斜上
            if (i - 1 >= 0) {//可以斜上
                i--;
                j++;
            } else {//否则直下
                i++;
                down = true;
            }
        }
        zArray[i][j] = s.charAt(k++);
        maxj = Math.max(maxj,j);
    }

    // 现在再开始搜集
    StringBuilder sb = new StringBuilder();
    for (int l = 0; l < m; l++) {
        for (int o = 0; o <= maxj; o++) {
            if(zArray[l][o]!='\0') sb.append(zArray[l][o]);
        }
    }

    //print2(zArray);

    return sb.toString();
}

最牛的做法肯定是找数组下标的规律了，就可以直接搜集了，
时间有限，就先不搞啦

TODO

15. 三数之和

hash+二重循环

public List<List<Integer>> threeSum(int[] nums) {
    //print(nums);

    Set<List<Integer>> ans = new HashSet<>();

    HashMap<Integer, Integer> map = new HashMap<>();

    for (int i = 0; i < nums.length; i++) {
        map.put(nums[i],i);
    }

    for (int i = 0; i < nums.length; i++) {
        for (int j = i+1; j < nums.length; j++) {
            int c = -(nums[i]+nums[j]);
            if(map.containsKey(c)&&map.get(c)>j){
                ArrayList<Integer> list = new ArrayList<>();
                list.add(nums[i]);
                list.add(nums[j]);
                list.add(c);
                Collections.sort(list);
                ans.add(list);
            }
        }
    }
    ArrayList<List<Integer>> lists = new ArrayList<>(ans);
    return lists;
}

优化，排序+双指针： n(n-1)/2 级别的O(n^2)

public List<List<Integer>> threeSum(int[] nums) {
    ArrayList<List<Integer>> lists = new ArrayList<>();
    int n = nums.length;
    Arrays.sort(nums);
    for (int i = 0; i < n; i++) {
        if(i>0&&nums[i]==nums[i-1]) continue;

        int l=i+1,r=n-1;
        while (l<r){
            int ts = nums[l]+nums[r];
            if(ts==-nums[i]) {
                ArrayList<Integer> list = new ArrayList<>();
                list.add(nums[i]);list.add(nums[l]);list.add(nums[r]);
                lists.add(list);
                //重复的这里也要跳过
                l++;r--;
                while (l<n&&nums[l-1]==nums[l]) l++;
                while (r>=0&&nums[r+1]==nums[r]) r--;
            }else if(ts<-nums[i]) l++;
            else r--;
        }
    }
    return lists;
}

167. 两数之和 II - 输入有序数组

“只使用常量级的额外空间” 不就是双指针了么？两端向中间靠拢搜索

public int[] twoSum(int[] numbers, int target) {
    int[] ans =  {-1,-1};
    int  i =0,j=numbers.length-1;
    while (i<j){
        if(numbers[i]+numbers[j]==target){
            ans[0] = i+1;ans[1]=j+1;
            break;
        }else if(numbers[i]+numbers[j]<target) i++;
        else j--;
    }
    return ans;
}

搞不懂哪里来的难度

209. 长度最小的子数组

开始打算前缀和+双指针，写一半发现不行
后来觉得，双指针+滑动窗口吧

果然是的

// 双指针滑动窗口比较好
public int minSubArrayLen(int target, int[] nums) {
    int n = nums.length;
    int ans = n + 1;
    int l = 0, r = 0;
    int sum = nums[0];
    while (r < n) {
        if (sum < target) {
            // 更新 右边窗口扩大一个
            r++;
            if(r<n) sum += nums[r];
        }
        else if (sum >= target){
            ans = Math.min(ans, r-l+1);
            // 更新 左边窗口缩小一个
            sum -= nums[l];
            l++;
        }
    }
    return ans == n + 1 ? 0 : ans;
}

36. 有效的数独

遍历3次和遍历1次的时间复杂度一样的，不如就暴力了

public boolean isValidSudoku(char[][] board) {
   HashSet<Character> set = new HashSet<>();
   for (int i = 0; i < 9; i++) {
       set.clear();
       for (int j = 0; j < 9; j++) {
           if (board[i][j] != '.' && !set.add(board[i][j]))  return false;
       }
   }
   for (int i = 0; i < 9; i++) {
       set.clear();
       for (int j = 0; j < 9; j++) {
           if (board[j][i] != '.' && !set.add(board[j][i]))  return false;
       }
   }

   for (int r = 0; r < 9; r += 3) {
       set.clear();
       for (int c = 0; c < 9; c += 3) {
           set.clear();
           for (int i = r; i < r + 3; i++) {
               for (int j = c; j < c + 3; j++) {
                   if (board[j][i] != '.' && !set.add(board[j][i])) return false;
               }
           }
       }
   }
   return true;
}

在这里插入图片描述

还有一种牺牲空间节省时间的做法
定义3种hash表即可
横竖的hash二维数组方便

9宫格的hash也2维数组，也是可以的，将下标转为九宫格左上即可，也就是j/3+(i/3)*3 正好也是0~9

public boolean isValidSudoku(char[][] board) {
    boolean[][] hashRow = new boolean[9][10];//第二维度10是因为数字范围是1~9
    boolean[][] hashCol = new boolean[9][10];
    boolean[][] hashBox = new boolean[9][10];

    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            if (board[i][j] != '.') {
                int k = board[i][j]-'0';
                if(hashRow[i][k]) return false;
                else hashRow[i][k]=true;

                if(hashCol[j][k]) return false;
                else hashCol[j][k]=true;

                int index = j/3+i/3*3;
                if(hashBox[index][k]) return false;
                else hashBox[index][k] = true;
            }
        }
    }

    return true;
}

代码简单一点,时间上竟然差不多，空间也差不多
在这里插入图片描述

54. 螺旋矩阵

最简单的思路就是DFS的思路，一直走就行了

boolean judge(int i, int j, int m, int n, boolean[][] visited) {
    if (i < 0 || i >= m || j < 0 || j >= n || visited[i][j]) return false;
    return true;
}
public List<Integer> spiralOrder(int[][] matrix) {
    ArrayList<Integer> ans = new ArrayList<>();
    int dir = 0;//0右 1下 2左 3上
    int m = matrix.length, n = matrix[0].length;
    int i = 0, j = 0;
    boolean[][] visited = new boolean[m][n];
    while (ans.size() < m * n) {
        if (!visited[i][j]) {
            ans.add(matrix[i][j]);
            visited[i][j] = true;
        }

        if (dir == 0) {//右
            if (judge(i, j + 1, m, n, visited)) j++;
            else dir = (dir + 1) % 4;
        } else if (dir == 1) {//下
            if (judge(i + 1, j, m, n, visited)) i++;
            else dir = (dir + 1) % 4;
        } else if (dir == 2) {//左
            if (judge(i, j - 1, m, n, visited)) j--;
            else dir = (dir + 1) % 4;
        } else {//只能是 上 了
            if (judge(i - 1, j, m, n, visited)) i--;
            else dir = (dir + 1) % 4;
        }
    }
    return ans;
}

非常简单的思路，时间上也过得去，就是空间上多了一个visited数组
在这里插入图片描述

289. 生命游戏

先暴力拿分（不考虑空间）

// 查找x,y周围8个区域v的数量
int findOnes(int[][] board,int x,int y){
    int ans = 0;
    int m = board.length;
    int n = board[0].length;
    for (int i = x-1; i <= x+1; i++) {
        if(i<0||i>=m) continue;
        for (int j = y-1; j <= y+1; j++) {
            if(j<0||j>=n) continue;
            if(i==x&&j==y) continue;
            if(1==board[i][j])
                ans++;
        }
    }
    return ans;
}

public void gameOfLife(int[][] board) {
    ArrayList<int[]> change = new ArrayList<>();
    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board[i].length; j++) {
            if(board[i][j]==1){
                int one = findOnes(board,i,j);
                if(one!=2&&one!=3) change.add(new int[] {i,j,0});
            }else {
                if(findOnes(board,i,j)==3) change.add(new int[] {i,j,1});
            }
        }
    }
    for (int[] ints : change) {
        board[ints[0]][ints[1]] = ints[2];
    }
}

在这里插入图片描述

再来优化空间：看了题解发现好简单：增加两个状态，表示复合状态-1表示先活后死(先1后0)，2表示先死后活(先0后1)

// 查找x,y周围8个区域v的数量
    int findOnes(int[][] board, int x, int y) {
        int ans = 0;

        int m = board.length;
        int n = board[0].length;
        for (int i = x - 1; i <= x + 1; i++) {
            if (i < 0 || i >= m) continue;
            for (int j = y - 1; j <= y + 1; j++) {
                if (j < 0 || j >= n) continue;
                if (i == x && j == y) continue;
                if (1 == board[i][j] || -1 == board[i][j])
                    ans++;
            }
        }
        return ans;
    }

    public void gameOfLife(int[][] board) {
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[i].length; j++) {
                if (board[i][j] == 1) {
                    int one = findOnes(board, i, j);
                    if (one != 2 && one != 3) board[i][j] = -1;//活->死
                } else {
                    if (findOnes(board, i, j) == 3) board[i][j] = 2;//死->活
                }
            }
        }

        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[i].length; j++) {
                if(board[i][j]==-1) board[i][j]=0;
                else if(board[i][j] == 2) board[i][j]=1;
            }
        }

    }

在这里插入图片描述
空间不降反增

算了，越优化，越差

57. 插入区间

核心中的核心：

不想妄想只用数组解决，一定要用List，不定长数组，否则太麻烦啦，还得提前判断长度，太难了，只能动态判断
一定要动态收集区间，先找位置，也不行，太麻烦了

public int[][] insert(int[][] intervals, int[] newInterval) {
    ArrayList<int[]> list = new ArrayList<>();

    if (intervals == null || intervals.length == 0) {
        list.add(newInterval);
    } else {
        int a = newInterval[0];
        int b = newInterval[1];
        int m = intervals.length;

        /*然后这里写自己的逻辑  否则会非常麻烦的 别没事找事  怎么简单怎么来*/

        
    }

    int[][] ans = new int[list.size()][2];
    for (int i = 0; i < list.size(); i++) {
        ans[i] = list.get(i);
    }
    return ans;
}

public int[][] insert(int[][] intervals, int[] newInterval) {
   ArrayList<int[]> list = new ArrayList<>();

   if (intervals == null || intervals.length == 0) {
       list.add(newInterval);
   } else {
       int a = newInterval[0];
       int b = newInterval[1];
       int m = intervals.length;

       /*然后这里写自己的逻辑  否则会非常麻烦的 别没事找事  怎么简单怎么来*/
       boolean inserted = false;
       for (int i = 0; i < m; i++) {
           int x = intervals[i][0];
           int y = intervals[i][1];

           int e1, e2;
           if(b<x&&!inserted){
               list.add(newInterval);
               list.add(intervals[i]);
               inserted = true;
           }else if (a <= y&&!inserted) {
               e1 = Math.min(a, x);
               e2 = Math.max(b, y);
               list.add(new int[]{e1, e2});
               inserted = true;
           } else {
               // 正常比较
               if (list.size() == 0 || list.get(list.size() - 1)[1] < x) {
                   list.add(intervals[i]);
               } else {
                   list.get(list.size() - 1)[1] = Math.max(y,b);
               }
           }

       }
       if(!inserted) list.add(newInterval);
   }

   int[][] ans = new int[list.size()][2];
   for (int i = 0; i < list.size(); i++) {
       ans[i] = list.get(i);
   }
   return ans;
}

在这里插入图片描述

看了题解，有一种思路更好的算法：

public int[][] insert(int[][] intervals, int[] newInterval) {
    ArrayList<int[]> list = new ArrayList<>();

    int left = newInterval[0];
    int right = newInterval[1];
    int n = intervals.length;
    int i = 0;

    // 左边区间外的全部搜集好
    while (i<n&&intervals[i][1]<left){
        list.add(intervals[i++]);
    }

    // 中间重叠区间先合并好
    while (i<n&&intervals[i][0]<=right){
        left = Math.min(left,intervals[i][0]);
        right = Math.max(right,intervals[i][1]);//合并区间的关键两步操作  太强了
        i++;
    }
    // 加入合并好的区间
    list.add(new int[]{left,right});

    // 右边区间外的
    while (i<n&&intervals[i][0]>right){
        list.add(intervals[i++]);
    }

    return list.toArray(new int[0][]);
}

整理一下;

public int[][] insert(int[][] intervals, int[] newInterval) {
    ArrayList<int[]> list = new ArrayList<>();

    int left = newInterval[0];
    int right = newInterval[1];
    int n = intervals.length;
    int i = 0;

    // 左边区间外的全部搜集好
    while (i<n&&intervals[i][1]<left) list.add(intervals[i++]);

    // 中间重叠区间先合并好
    while (i<n&&intervals[i][0]<=right){
        left = Math.min(left,intervals[i][0]);
        right = Math.max(right,intervals[i][1]);//合并区间的关键两步操作  太强了
        i++;
    }
    // 加入合并好的区间
    list.add(new int[]{left,right});

    // 右边区间外的
    while (i<n)  list.add(intervals[i++]);

    return list.toArray(new int[0][]);
}

整理最短：

public int[][] insert(int[][] intervals, int[] newInterval) {
    ArrayList<int[]> list = new ArrayList<>();
    int i = 0;

    // 左边区间外的全部搜集好
    while (i<intervals.length&&intervals[i][1]<newInterval[0]) list.add(intervals[i++]);

    // 中间重叠区间先合并好
    while (i<intervals.length&&intervals[i][0]<=newInterval[1]){
        newInterval[0] = Math.min(newInterval[0],intervals[i][0]);
        newInterval[1] = Math.max(newInterval[1],intervals[i][1]);//合并区间的关键两步操作  太强了
        i++;
    }
    // 加入合并好的区间
    list.add(newInterval);

    // 右边区间外的
    while (i<intervals.length)  list.add(intervals[i++]);

    return list.toArray(new int[0][]);
}

71. 简化路径

还挺简单的

public String simplifyPath(String path) {
   String[] split = path.split("/");

   List<String> list = new LinkedList<>();
   for (int i = 0; i < split.length; i++) {
       if(".".equals(split[i])||"".equals(split[i])) continue;
       if("..".equals(split[i])){
           if(list.size()>0) list.remove(list.size()-1);
       }else list.add(split[i]);
   }

   //print(list);
   StringBuilder ans = new StringBuilder();
   for (String s : list) {
       ans.append("/").append(s);
   }
   return ans.length()>0?ans.toString():"/";
}

150. 逆波兰表达式求值

后缀表达式==逆波兰表达式专门用于计算的表达式
求值特别方便，遇到运算符就取出两个数进行计算即可

int count(char opt,int a,int b){
    if(opt=='+') return a+b;
    else if(opt=='-') return a-b;
    else if(opt=='*') return a*b;
    else return a/b;
}

public int evalRPN(String[] tokens) {
    int ans = 0;
    Deque<Integer> nums = new LinkedList<>();
    Deque<Character> opt = new LinkedList<>();
    for (String token : tokens) {
        if(token.length()>1||Character.isDigit(token.charAt(0))){
            nums.push(Integer.valueOf(token));
        }else {
            int b = nums.pop();//先出来的是第二个操作数
            int a = nums.pop();
            nums.push(count(token.charAt(0),a,b));
        }
    }
    return nums.pop();
}

224. 基本计算器

先写好模板，再编码

模板（字符串处理无误）

// 就是中缀表达式求职 不能拿
public int calculate(String s) {
    int ans = 0;
    Deque<Character> opt = new LinkedList<>();
    Deque<Integer> nums = new LinkedList<>();

    int sign = 1;
    for (int i = 0; i < s.length(); i++) {
        char c = s.charAt(i);

        if (i == 0 && (c == '-' || c == '+')) {
            if (c == '-') sign = -1;
            continue;
        }

        if(' '==c) continue;

        // 运算符
        if (c=='+'||c=='-'||c=='('||c==')') {
            
            // 先不管计算 先直接入栈
            opt.push(c);
        } else {
            // 数字  但是长度可能很长
            int k = 0;
            while (Character.isDigit(s.charAt(i))){
                k = k*10 + (s.charAt(i) - '0');
                i++;//上面还要用到i  不能尽早i++
            }
            nums.push(k);
            i--;//for循环里还会i++ (刚i-1表示处理完i-1)
        }
    }

    return ans;
}

求值（中缀的规律）

第一版

// 就是中缀表达式求职 不能拿
public int calculate(String s) {
    Deque<Character> opt = new LinkedList<>();
    Deque<Integer> nums = new LinkedList<>();

    // 特殊情况 字符串层面 纠正一下吧
    if (s.charAt(0) == '-') s = "0" + s;//换成nums.push(0);也行
    s = s.replace(" ", "");
    s = s.replace("(-", "(0-");

    for (int i = 0; i < s.length(); i++) {
        char c = s.charAt(i);
        if (' ' == c) continue;
        // 运算符
        if (c == '+' || c == '-' || c == '(' || c == ')') {
            if (c == '(' || opt.size() == 0 || (opt.peek() == '(' && c != ')')) {
                opt.push(c);
            } else {
                //不是加就是减喽 而且 栈顶不是+ 就是 -  (因为+-同级 所以这里的+-也都要计算到最近一个'('或者栈空)
                while (!opt.isEmpty() && opt.peek() != '(') {
                    char op = opt.pop();
                    int b = nums.pop();
                    int a = nums.pop();
                    if (op == '+') nums.push(a + b);
                    else nums.push(a - b);
                }
                if (c == ')') opt.pop();
                else opt.push(c);//加入符号
            }
        } else {
            // 数字  但是长度可能很长
            int k = 0;
            while (i < s.length() && Character.isDigit(s.charAt(i))) {
                k = k * 10 + (s.charAt(i) - '0');
                i++;//上面还要用到i  不能尽早i++
            }
            nums.push(k);
            i--;//for循环里还会i++ (刚i-1表示处理完i-1)
        }
    }

    while (!opt.isEmpty()) {
        char op = opt.pop();
        int b = nums.pop();
        int a = nums.pop();
        if (op == '+') nums.push(a + b);
        else nums.push(a - b);
    }

    return nums.pop();
}

138. 复制带随机指针的链表

自己做法，hash表，但是没真正用对Hash表

public Node copyRandomList(Node head) {
    HashMap<Node, Node> map = new HashMap<>();

    Node ans = new Node(-1);
    Node tail_ans = ans;

    int k = 0;
    Node tail = head;
    while (tail!=null){
        Node node = new Node(tail.val);
        map.put(tail,node);//旧到新的映射  方便确定random

        tail_ans.next = node;

        tail = tail.next;
        tail_ans = tail_ans.next;
    }
    tail_ans = ans.next;//注意第一个节点是 ans.next
    tail = head;
    while (tail!=null) {
        tail_ans.random = map.get(tail.random);//key是null   value应该默认就是null了
        tail = tail.next;
        tail_ans = tail_ans.next;
    }
    return ans.next;
}

看题解的做法，思路差不多，但是感觉对Hash表的认识更加深刻

public Node copyRandomList(Node head) {
    HashMap<Node, Node> map = new HashMap<>();
    Node ans = new Node(-1);

    Node tail0 = head;
    while (tail0!=null){
        map.put(tail0,new Node(tail0.val));
        tail0=tail0.next;
    }

    Node tail1 = ans;
    tail0 = head;
    while (tail0!=null){
        tail1.next = map.get(tail0);
        tail1.next.random = map.get(tail0.random);//注意是next.random 链表通过前驱来操作

        tail0 = tail0.next;
        tail1 = tail1.next;
    }

    return ans.next;
}

官解有一种递归写法

核心思想还是做映射，key(head)->value(newHead)一一影视，然后每次都要处理下head.next，链表就是前驱处理嘛（或者说父节点创建完后理解处理孩子节点），孩子的赋值可以递归操作

思路差不多，空间可能差点，但是代码看起来清爽多了

HashMap<Node, Node> cache = new HashMap<>();
public Node copyRandomList(Node head) {
    if (head == null) return null;
    if (!cache.containsKey(head)) {
        Node newHead = new Node(head.val);
        cache.put(head,newHead);
        newHead.next = copyRandomList(head.next);
        newHead.random = copyRandomList(head.random);
    }
    return cache.get(head);
}

92. 反转链表 II

一趟遍历可以解决，就一趟遍历呗，怎么简单怎么来呗

public ListNode reverseBetween(ListNode head, int left, int right) {
    if (left == right) return head;
    ListNode ans = new ListNode(-1);
    ListNode tail = ans;
    int k = 0;
    boolean isTail = true;
    ListNode tailRv = null;
    ListNode p = head;
    while (p != null) {
        k++;
        if (k < left) {//前面的顺序接上
            tail.next = p;
            tail = tail.next;
            p = p.next;
        } else if (k <= right) {
            if (isTail) {//记录下翻转后的尾结点
                isTail = false;
                tailRv = p;
            }
            ListNode next = p.next;//中间部分头插法实现逆置
            p.next = tail.next;
            tail.next = p;
            p = next;
        } else {
            tailRv.next = p;//尾结点后面顺序接上
            tailRv = tailRv.next;
            p=p.next;
        }
    }

    tailRv.next=null;

    //tailRv.next = null;
    return ans.next;
}

82. 删除排序链表中的重复元素 II

美团一面真题，当时写得很麻烦，采用的是摘节点的思路
二刷简单多了，直接给原来链表加上一个头节点，然后直接在原来链表上删除

public ListNode deleteDuplicates(ListNode head) {
    // 加上头节点方便操作
    ListNode ans = new ListNode(-1);
    ans.next = head;
    ListNode p = ans;

    while (p.next != null) {
        if (p.next.next == null) break;
        if (p.next.val == p.next.next.val) {
            int val = p.next.val;
            while (p.next!=null&&p.next.val == val)
                p.next = p.next.next;
        }else {//删除后p是合适的前驱了  未删除时才需要移动
            p = p.next;
        }
    }

    return ans.next;
}

链表的题目，想想递归吧

TODO

61. 旋转链表

直接后k个节点摘下来，再放到前面链接起来

public ListNode rotateRight(ListNode head, int k) {
    if(head==null||k==0||head.next==null) return head;
    ListNode t = head;
    int len = 0;
    while (t!=null) {
        len++;
        t=t.next;
    }
    k %= len;
    if(k==0) return head;

    // 没办法 k>len  还是得先知道长度  两趟遍历少不了
    ListNode p=head,q=head;
    for (int i = 1; i < len; i++){
        q = q.next;
        if(i<len-k) p = p.next;
    }

    ListNode ans = p.next;
    p.next = null;
    q.next = head;

    return ans;
}

闭合为环，指定位置再断开

public ListNode rotateRight(ListNode head, int k) {
    if(head==null) return head;

    // 闭合为环
    int len = 0;
    ListNode tail = head;
    while (tail.next!=null) {
        tail = tail.next;
        len++;
    }
    tail.next = head;
    k %= len+1;

    //合适处断开
    int T = len-k;
    tail = head;
    while (T-->0) tail=tail.next;
    ListNode ans = tail.next;
    tail.next = null;

    return ans;
}

86. 分隔链表

paper tiger ：链表的题其实都不难，别着急，慢慢厘清思路就行了

public ListNode partition(ListNode head, int x) {

    ListNode head1 = new ListNode();
    ListNode tail1 = head1;
    ListNode head2 = new ListNode();
    ListNode tail2 = head2;

    ListNode node = head;

    while (node!=null){
        if(node.val<x){
            tail1.next = node;
            tail1 = node;
        }else{
            tail2.next = node;
            tail2 = node;
        }
        node = node.next;
    }

    tail1.next = head2.next;
    tail2.next = null;

    return head1.next;
}

124. 二叉树中的最大路径和

方法1: 确定中间点，先序遍历每个节点作为中间一次

public int maxPathSum(TreeNode root) {
     if (root == null) {
         return 0;
     }

     // 遍历作为中间点的节点
     int sum = root.val;
     int left = maxPath(root.left, 0, 0);
     if (left > 0) {
         sum += left;
     }
     int right = maxPath(root.right, 0, 0);
     if (right > 0) {
         sum += right;
     }

     ans = Math.max(ans, sum);

     maxPathSum(root.left);
     maxPathSum(root.right);

     return ans;
 }

 private int ans = Integer.MIN_VALUE;

 // 以我为起点的所有连续路径的最大值 (可以做缓存)
 public int maxPath(TreeNode root, int sum, int max) {
     if (root == null) {
         return max;
     }

     sum += root.val;
     max = Math.max(max, sum);

     if (root.left != null) {
         max = Math.max(maxPath(root.left, sum, max), max);
     }

     if (root.right != null) {
         max = Math.max(maxPath(root.right, sum, max), max);
     }
     return max;

 }

方法2:优化 - 直接看的题解，求某节点为起点的最大连续路径长度竟然这么简单：后续遍历，简单DP的思想，好简单

调用一次根的递归，所有的最大贡献就都有了
思路还是有所区别的

个人感觉比较难想，得画图分析才行，然后别急

public int maxPathSum(TreeNode root) {
    maxPath(root);
    return ans;
}
private int ans = Integer.MIN_VALUE;
// 以我为起点的所有连续路径的最大值, 后续遍历DP思想即可
public int maxPath(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int left = Math.max(0, maxPath(root.left));
    int right = Math.max(0, maxPath(root.right));
    ans = Math.max(ans, root.val + left + right);

    // 千万注意这里返回的是以root 为起点的单路径最大长度 ！！！！
    return root.val + Math.max(left, right);
}

106. 从中序与后序遍历序列构造二叉树

先给一个懒人做法，时间很低，代码很简单

public TreeNode buildTree(int[] inorder, int[] postorder) {
        if (inorder.length == 0) return null;

        int val = postorder[postorder.length - 1];
        TreeNode root = new TreeNode(val);

        int k = 0;
        while (inorder[k] != val) k++;
        root.left = buildTree(
                Arrays.copyOfRange(inorder, 0, k),
                Arrays.copyOfRange(postorder, 0, k)
        );
        root.right = buildTree(
                Arrays.copyOfRange(inorder, k + 1, inorder.length),
                Arrays.copyOfRange(postorder, k, postorder.length - 1)
        );
        return root;
    }

再优化一下时间吧

public TreeNode buildTree(int[] inorder, int[] postorder) {
    return createTree(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
}

public TreeNode createTree(int[] inorder, int x1, int x2, int[] postorder, int y1, int y2) {
    //if (x1 == x2) return new TreeNode(inorder[x1]); // 单节点直接返回，这是出口 代码逻辑正确就不需要这个出口
    if (x1 > x2) return null;
    int val = postorder[y2];
    TreeNode root = new TreeNode(val);
    int k = x1;
    while (inorder[k] != val) k++;
    root.left = createTree(inorder, x1, k - 1, postorder, y1, y1 + (k - x1) - 1);
    root.right = createTree(inorder, k + 1, x2, postorder, y1 + (k - x1), y2 - 1);
    return root;
}

68. 文本左右对齐

此题复杂了一点，但其实模块化后并不难。
唯一的坑点就是：

每2个单词之间至少一个空格
行尾没有单词时得填充满空格
空格均匀分布指的是：5个空格，3个间隙，应该是2 2 1，而非3，1，1

第3点也是看leetcode官方题解才看懂，主要难点还是题意的理解
在这里插入图片描述

String getBlankStr(int n) {
    StringBuilder sb = new StringBuilder();
    while (n-- > 0) sb.append(' ');
    return sb.toString();
}

String getRow(List<String> temp, int maxWidth) {
    if (temp.size() == 1) return temp.get(0) + getBlankStr(maxWidth - temp.get(0).length());

    int strTotalLen = 0;
    for (String s : temp) strTotalLen += s.length();
    int blankTotalLen = maxWidth - strTotalLen;
    int blankNum = temp.size() - 1;
    // 总长度maxWidth   实际长度len  实际个数n+1  中间空隙n  需要添加的空格数blank
    // 空格的均匀分配很有讲究的
    int simpleBlankLenAvg = blankTotalLen / blankNum; // 但间隔 空格数  偏少
    int addBlankNum = blankTotalLen % blankNum; // 前addBlankNum个空隙得多一个空格
    ArrayList<String> ret = new ArrayList<>();
    StringBuilder ans = new StringBuilder(temp.get(0));
    for (int i = 1; i < temp.size(); i++) {
        if (i<=addBlankNum) ans.append(getBlankStr(simpleBlankLenAvg+1));
        else ans.append(getBlankStr(simpleBlankLenAvg));
        ans.append(temp.get(i));
    }
    return ans.toString();
}

public List<String> fullJustify(String[] words, int maxWidth) {
    ArrayList<String> ans = new ArrayList<>();
    int len = 0;
    ArrayList<String> temp = new ArrayList<>();

    for (String word : words) {
        if (len + word.length() + 1 <= maxWidth + 1) {//最后一个末尾的空格是可以不需要的
            len += word.length() + 1;
            temp.add(word);
        } else {
            ans.add(getRow(temp, maxWidth));
            // 首行第一个直接进来即可
            temp.clear();
            temp.add(word);
            len = word.length() + 1;
        }
    }

    // 最后一行的需要单独处理
    StringBuilder sb = null;
    if (temp.size() > 0) {
        sb = new StringBuilder(temp.get(0));
        for (int i = 1; i < temp.size(); i++) {
            sb.append(" ").append(temp.get(i));
        }
        String str = sb.toString();
        ans.add(str + getBlankStr(maxWidth - str.length())); // 测试代码写错了 所以末尾要加空格
    }
    return ans;
}

117. 填充每个节点的下一个右侧节点指针 II

按行的层序遍历，不难

public Node connect(Node root) {
    if (root == null) return null;
    // 层序遍历
    Deque<Node> q = new LinkedList<>();
    q.push(root);
    // 一层一层地处理
    while (!q.isEmpty()) {
        int T = q.size();
        Node pre = null;
        while (T-- > 0) {
            Node curt = q.poll();
            if (curt.left != null) q.offer(curt.left);
            if (curt.right != null) q.offer(curt.right);
            if (pre != null) pre.next = curt;
            pre = curt;
        }
        pre.next = null;
    }
    return root;
}

30. 串联所有单词的子串▲

30. 串联所有单词的子串

先暴力通关一下，竟然过了

void add(String word, HashMap<String, Integer> wordHash) {
    Integer old = wordHash.getOrDefault(word, 0);
    wordHash.put(word, old + 1);
}

boolean pop(String word, HashMap<String, Integer> wordHash) {
    Integer old = wordHash.getOrDefault(word, 0);
    if (old <= 0) return false;
    wordHash.put(word, old - 1);
    return true;
}

HashMap<String, Integer> copy(HashMap<String, Integer> wordHash) {
    HashMap<String, Integer> copied = new HashMap<>();
    copied.putAll(wordHash);
    return copied;
}

public List<Integer> findSubstring(String s, String[] words) {
    ArrayList<Integer> ans = new ArrayList<>();
    if (s.length() == 0 || words.length == 0) return ans;
    HashMap<String, Integer> wordHash = new HashMap<>();
    for (String word : words) add(word, wordHash);
    int n = words[0].length();
    int len = n * words.length;

    for (int i = 0; i < s.length(); i++) {
        HashMap<String, Integer> hash = copy(wordHash);
        for (int j = i; j + n <= s.length(); j += n) {//<= 因为第j+n不会被截取到 是右开区间
            String sub = s.substring(j, j + n);
            if (!pop(sub, hash)) break;
            if (j + n - i == len) { // 本次是j~j+n 终点是j+n
                ans.add(i);
                break;
            }
        }
    }
    return ans;
}

优化做法，确定搜索起点，不用每次都回退

看了题解，太妙了，果然，做hard才会有提升，否则只是简单的维持功力不退

单个长度 oneLen
这样，从0~oneLen-1 分别做一次起点，每次截取oneLen个单词，这样每次不必回退到起点（也是为啥 “可以以【任意顺序】返回答案”），可以维持滑动窗口，

重复了, 窗口起点后移oneLen,可以继续搜索
不匹配，窗口起点直接移动到当前终点即可
维护两个Hash表，想办法比较两个Hash表是否一致，不用每次复制一个Hash表

无以言表了，滑动窗口用得太妙了

public List<Integer> findSubstring(String s, String[] words) {
    ArrayList<Integer> ans = new ArrayList<>();
    if (s.length() == 0 || words.length == 0) return ans;

    int oneLen = words[0].length();
    int num = words.length;
    int totalLen = oneLen * num;

    HashMap<String, Integer> map1 = new HashMap<>();
    for (String word : words) {
        map1.put(word, map1.getOrDefault(word, 0) + 1);
    }

    for (int i = 0; i < oneLen; i++) {
        HashMap<String, Integer> map2 = new HashMap<>(); // 也就新建 oneLen次，这就是好处
        int l = i, r = i; // 滑动窗口左右边界

        while (r + oneLen <= s.length()) { // <= 最后一个是 右开区间
            String w = s.substring(r, r + oneLen);
            r += oneLen;
            if (!map1.containsKey(w)) {
                l = r;
                map2.clear(); // 清空重新开始
            } else {
                map2.put(w, map2.getOrDefault(w, 0)+1);

                // 如果超了 由于连续性需要剔除上一个w(这一个要进窗口)
                // 从前面一个个单词地剔除出窗口，直到剔除了w
                while (map2.get(w) > map1.get(w)) { // 不确定本次窗口头的是不是w，所以需要while循环不断尝试
                    String sOut = s.substring(l, l + oneLen);
                    map2.put(sOut, map2.getOrDefault(sOut, 0) - 1); // 窗口内的，map2中一定有的
                    l += oneLen;
                }

                if (r-l == totalLen){
                    // 找到了
                    ans.add(l);

                    // 仍然是窗口内去掉一个就行了 ★★  剩下的可以接着匹配
                    String sOut = s.substring(l, l + oneLen);
                    map2.put(sOut, map2.getOrDefault(sOut, 0) - 1); // 窗口内的，map2中一定有的
                    l += oneLen;
                }
            }
        }
    }
    return ans;
}

76. 最小覆盖子串▲

76. 最小覆盖子串

自己写得滑动窗口，足足针对6个用例进行了修改，水平有待提高哇

private void add(HashMap<Character, Integer> map, Character c) {
    Integer old = map.getOrDefault(c, 0);
    map.put(c, old + 1);
}

private boolean pop(HashMap<Character, Integer> map, Character c) {
    Integer old = map.getOrDefault(c, 0);
    map.put(c, old - 1);
}

// 窗口起点缩小
private int rightMoveWindow(char[] ss, int l, HashMap<Character, Integer> map1, HashMap<Character, Integer> map2) {
    if (l < ss.length) pop(map2, ss[l++]); // 维护了第一个一定是t中字符
    while (l < ss.length) {
        if (map2.getOrDefault(ss[l], 0) == 0) l++;
        else if (map2.get(ss[l]) > map1.get(ss[l])) pop(map2, ss[l++]);
        else break;
    }
    return l;
}

public String minWindow(String s, String t) {
    String ans = "";
    HashMap<Character, Integer> map1 = new HashMap<>();
    for (int i = 0; i < t.length(); i++) add(map1, t.charAt(i));

    char[] ss = s.toCharArray();
    int l = 0, r = 0;
    int count = 0;
    HashMap<Character, Integer> map2 = new HashMap<>();

    // 维护l一定是有效字符
    while (l < s.length() && !map1.containsKey(ss[l])) l++;
    r = l;
    
    while (r < s.length()) {
        char c = ss[r++];
        if (map1.containsKey(c)) {
            add(map2, c);
            if (map2.get(c) <= map1.get(c)) count++; //刚刚add的，可以等于
            else {
                //pop(map2,c); //不出去也行 有些用例则不能出去
                if (ss[l] == c) {//起点重复了，可以缩窗口了
                    l = rightMoveWindow(ss, l, map1, map2);
                }
            }

            if (count == t.length()) {
                if ("".equals(ans)) ans = s.substring(l, r);
                else if (ans.length() > r - l) ans = s.substring(l, r);
                l = rightMoveWindow(ss, l, map1, map2);
                count--;
            }
        }

    }
    return ans;
}

简化一下

// 窗口起点缩小
private int rightMoveWindow(char[] ss, int l, HashMap<Character, Integer> map1, HashMap<Character, Integer> map2) {
    if (l < ss.length) map2.put(ss[l],map2.getOrDefault(ss[l++],0)-1);//pop(map2, ss[l++]); // 维护了第一个一定是t中字符
    while (l < ss.length) {
        if (map2.getOrDefault(ss[l], 0) == 0) l++;
        else if (map2.get(ss[l]) > map1.get(ss[l])) map2.put(ss[l],map2.getOrDefault(ss[l++],0)-1);
        else break;
    }
    return l;
}

public String minWindow(String s, String t) {
    String ans = "";
    HashMap<Character, Integer> map1 = new HashMap<>();
    for (int i = 0; i < t.length(); i++) map1.put(t.charAt(i), map1.getOrDefault(t.charAt(i), 0) + 1);
    char[] ss = s.toCharArray();
    int l = 0, r = 0;
    int count = 0;
    HashMap<Character, Integer> map2 = new HashMap<>();
    // 维护l一定是有效字符
    while (l < s.length() && !map1.containsKey(ss[l])) l++;
    r = l;
    while (r < s.length()) {
        char c = ss[r++];
        if (map1.containsKey(c)) {
            map2.put(c, map2.getOrDefault(c, 0) + 1);
            if (map2.get(c) <= map1.get(c)) count++; //刚刚add的，可以等于
            else if (ss[l] == c) l = rightMoveWindow(ss, l, map1, map2); //起点重复了，可以缩窗口了
            //pop(map2,c); //不出去也行 有些用例则不能出去

            if (count == t.length()) {
                if ("".equals(ans)) ans = s.substring(l, r);
                else if (ans.length() > r - l) ans = s.substring(l, r);
                l = rightMoveWindow(ss, l, map1, map2);
                count--;
            }
        }
    }
    return ans;
}

再看下别人怎么写的
果然高手无处不在
总有些奇才

因为对象是字符，可以自己写hash表节省时间，
简单hash的记录方式也变得非常简单

public String minWindow(String S, String T) {
    char[] s = S.toCharArray();
    char[] t = T.toCharArray();
    int[] hash = new int[128];
    for (char c : t) hash[c - 'A']++;
    int count = t.length;

    int l = 0, start = -1, end = 0;
    for (int r = 0; r < s.length; r++) {
        if (--hash[s[r] - 'A'] >= 0) count--; // 根据是否>=0来判断，太妙了

        while (count == 0) {// 全包含了，找下起点l   while不断找起点太妙
            if (++hash[s[l++] - 'A'] > 0) {
                count++; // 同时也是while结束的条件
                if (r - l + 1 < end - start || start == -1) {// 这里做的比较
                    start = l - 1; // 最后一次正好l++ 将第一个合法的出去了
                    end = r;
                }
            }
        }
    }
    return start == -1 ? "" : S.substring(start, end + 1);
}

222. 完全二叉树的节点个数

明确时间复杂度问题

$O(log^2n)$ < $O (n)$
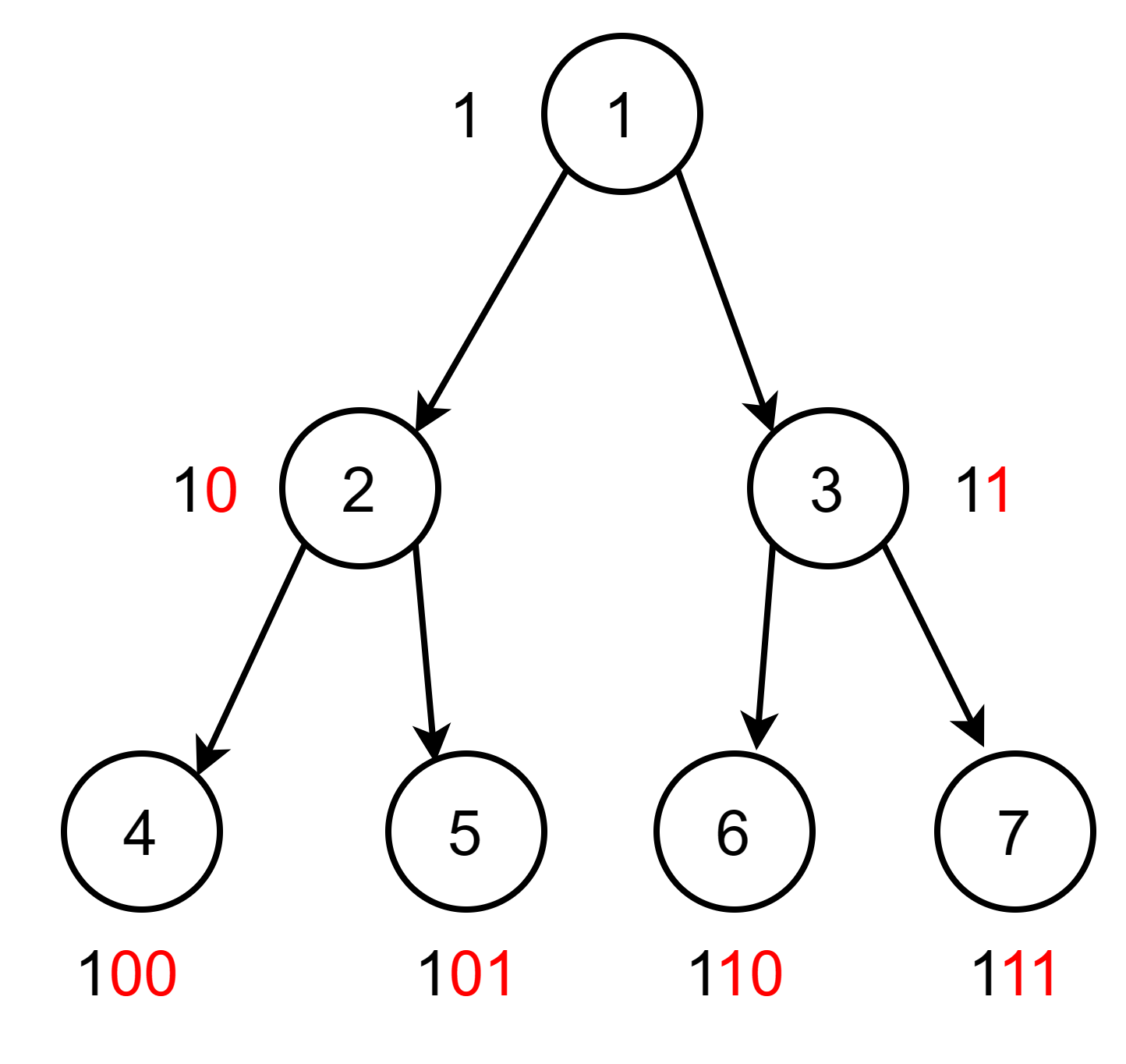
在这里插入图片描述

明确完全二叉树从1开始编号是的优美规律

高位都是1不看，从次高位开始看，若为0就往左走，若是1就往右走，正好是根到该节点的路径。
在这里插入图片描述

$1^n$ == $2 << n$

// 判断从1开始编号，第k个节点是否存在
public boolean exist(TreeNode root,int k){
    char[] s = Integer.toBinaryString(k).toCharArray();
    //prints(k,s);
    TreeNode node = root; // 竟然会影响到原来的root
    for (int i = 1; i < s.length; i++) {
        node = s[i]=='0'?node.left:node.right; // 注意是字符'0'不是数字0
        if(node==null) return false;
    }
    return true;
}

public int countNodes(TreeNode root) {
    if(root==null) return 0;

    // 先确定几层，快速确定范围
    int h = 1;
    TreeNode node = root;
    while (node != null) {
        node = node.right;
        h++;
    }

    // 2^(h-1)-1
    // 2^n == 2<<n
    int low = (1 << (h - 1)) - 1;// 2^(h-1)-1
    int high = (1 << h) - 1; // 2^h -1
    //prints(h, low, high);
    while (low<=high){
        int mid = (low+high)/2;
        if(exist(root,mid)) low = mid+1;
        else high = mid-1;
    }
    return low-1;
}

25. K 个一组翻转链表▲

25. K 个一组翻转链表

先自己暴力做一次，因为辅助函数内申请了头结点，所以空间复杂度应该是O(len/k)不是O(1), 时间上0ms没问题。

ListNode reverse(ListNode head) {
    ListNode ans = new ListNode();
    ListNode node = head;
    while (node != null) {
        ListNode temp = node.next;
        node.next = ans.next;
        ans.next = node;
        node = temp;
    }
    return ans.next;
}

public ListNode reverseKGroup(ListNode head, int k) {
    if(head==null) return null;
    ListNode nHead = head, nTail = head;

    ListNode preTail=null;
    int n = 0;
    while (nTail != null) {
        n++;
        if (n % k == 0) {
            ListNode temp = nTail.next;
            nTail.next = null;
            ListNode ans = reverse(nHead);

            if(n==k) head = ans;
            else preTail.next = ans;
            preTail = nHead;

            nTail = temp;
            nHead = temp;
        }else {
            nTail = nTail.next;
        }
    }
    if(n%k!=0) preTail.next = nHead;
    return head;
}

优化做法
看了题解，做法和我差不多，但是他的逆转函数没有申请头结点，所以是O(1),然后画图之后思路也简单了许多
自己再试着写一遍吧

主要就是逆置方法不需要头结点

ListNode reverse(ListNode head) {
    ListNode ans = null;
    ListNode curt = head;
    while (curt != null) {
        ListNode temp = curt.next;
        curt.next = ans;
        ans = curt;
        curt = temp;
    }
    return ans;
}

173. 二叉搜索树迭代器

直接遍历的简单做法

public class BSTIterator extends Solution {

    TreeNode root;
    int len = 0;
    int curt = -1;
    List<Integer> inList = new ArrayList();

    void inOrder(TreeNode root) {
        if (root == null) return;
        inOrder(root.left);
        inList.add(root.val);
        inOrder(root.right);
    }

    public BSTIterator(TreeNode root) {
        this.root = root;
        inOrder(root);
    }

    public int next() {
        return inList.get(++curt);
    }

    public boolean hasNext() {
        return curt + 1 < inList.size();
    }
}

题解的自己写栈实现中序遍历的方法（虽然不好，但是得掌握）

todo

130. 被围绕的区域

初步思想：O组成的连通分量不含边界
每次一个完整的连通分量要遍历完毕

自己连通分量的做法，很慢

public void solve(char[][] board) {
    // 寻找'O'的连通分量
    this.M = board.length;
    this.N = board[0].length;
    this.board = board;
    this.visited = new boolean[M][N];

    for (int i = 1; i < M - 1; i++) {
        for (int j = 1; j < N - 1; j++) {
            if (!visited[i][j] && board[i][j] == 'O') {
                fill.clear();
                flag = true;
                dfs(i,j);
                if (flag) {
                    // 被包围，填充
                    for (int[] pos : fill) {
                        board[pos[0]][pos[1]] = 'X';
                    }
                }
            }
        }
    }


}

int M, N;
char[][] board;
boolean[][] visited;
ArrayList<int[]> fill = new ArrayList<>();
boolean flag = true;

boolean judge(int x, int y) {
    return x >= 0 && x < M && y >= 0 && y < N && !visited[x][y] && board[x][y] == 'O';
}

void dfs(int x, int y) {
    if (x == 0 || x == M - 1 || y == 0 || y == N - 1) flag = false;
    visited[x][y] = true;
    fill.add(new int[]{x, y});

    boolean f1 = false, f2 = false, f3 = false, f4 = false;
    if (judge(x - 1, y)) dfs(x - 1, y);
    if (judge(x + 1, y)) dfs(x + 1, y);
    if (judge(x, y - 1)) dfs(x, y - 1);
    if (judge(x, y + 1)) dfs(x, y + 1);
    // 保证一次连通分量全部遍历到 全部标记到
}

看了题解才发现自己蠢，反过来不就行了，只遍历边界的O连通分量，剩下的O就是被包围的，这样应该会节省点时间

public void solve(char[][] board) {
    // 寻找'O'的连通分量
    this.M = board.length;
    this.N = board[0].length;
    this.board = board;

    // 左边界和右边界
    for (int i = 0; i < M; i++) {
        if (board[i][0] == 'O') dfs(i, 0);
        if (board[i][N - 1] == 'O') dfs(i, N - 1);
    }

    // 上边界和下边界
    for (int j = 0; j < N; j++) {
        if (board[0][j] == 'O') dfs(0, j);
        if (board[M - 1][j] == 'O') dfs(M - 1, j);
    }

    // Z修改为O，O修改为X
    for (int i = 0; i < M; i++) {
        for (int j = 0; j < N; j++) {
            if (board[i][j] == 'Z') board[i][j] = 'O';
            else if (board[i][j] == 'O') board[i][j] = 'X';
        }
    }

}

int M, N;
char[][] board;

boolean judge(int x, int y) {
    return x >= 0 && x < M && y >= 0 && y < N && board[x][y] == 'O';
}


void dfs(int x, int y) {
    board[x][y] = 'Z'; // 临时修改为Z，不需要visited了
    if (judge(x - 1, y)) dfs(x - 1, y);
    if (judge(x + 1, y)) dfs(x + 1, y);
    if (judge(x, y - 1)) dfs(x, y - 1);
    if (judge(x, y + 1)) dfs(x, y + 1);
    // 保证一次连通分量全部遍历到 全部标记到
}

133. 克隆图

简单DFS实现一下，个人第一想法，代码简单，效率却并不高

public Node cloneGraph(Node root) {
    if(root==null) return null;
    HashMap<Integer, Node> map = new HashMap<>();
    dfs(root,map);
    return map.get(1);
}

private void dfs(Node root, Map<Integer, Node> map) {
    map.put(root.val, new Node(root.val));
    for (Node neighbor : root.neighbors) {
        if (!map.containsKey(neighbor.val)) dfs(neighbor, map);
        map.get(root.val).neighbors.add(map.get(neighbor.val)); // 放在判断外面，才能保证所有无向边都在 ！！！千万不要放到if判断里面
    }
}

在这里插入图片描述
看了一下题解，只写了一个函数：24ms, 其实差别不算大，算法思路完全一样的，所以还行吧

请添加图片描述