matlab 线性卷积与圆周卷积
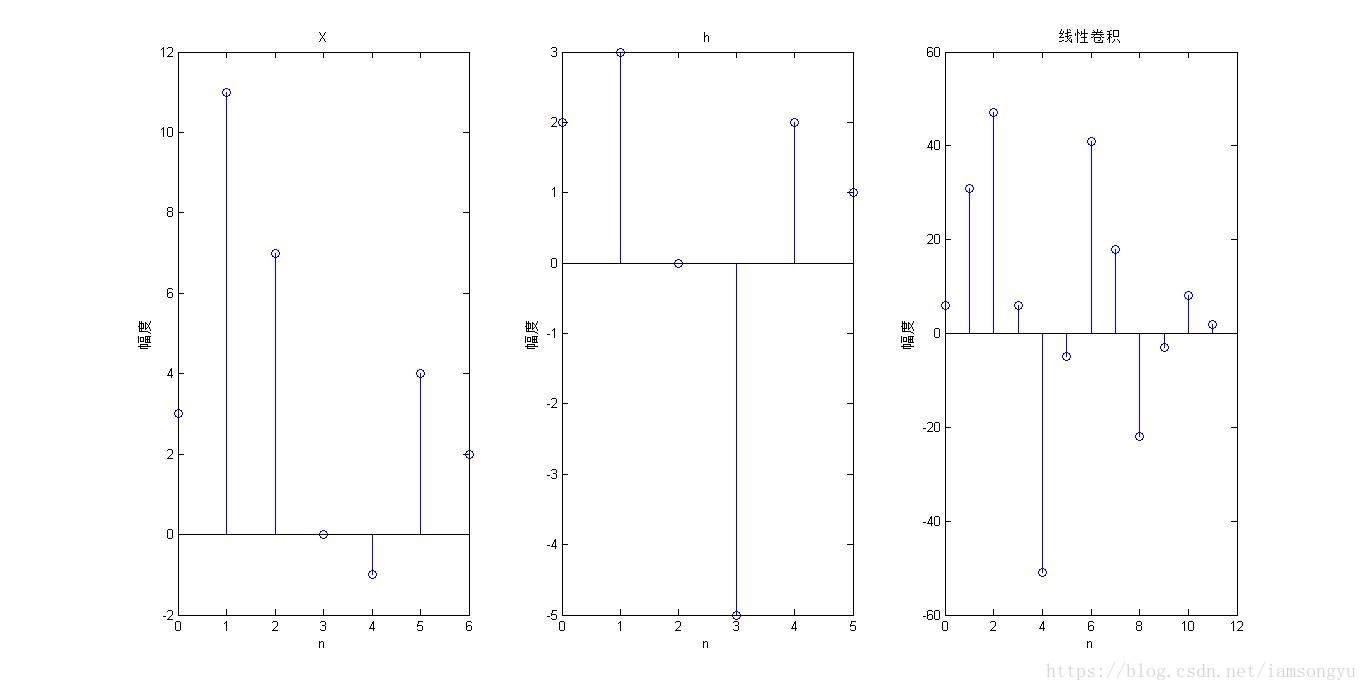
- 给出序列x=[3,11,7,0,-1,4,2],h=[2,3,0,-5,2,1];用两种方法求两者的线性卷积y,对比结果。
a) 直接调用matlab内部函数conv来计算。
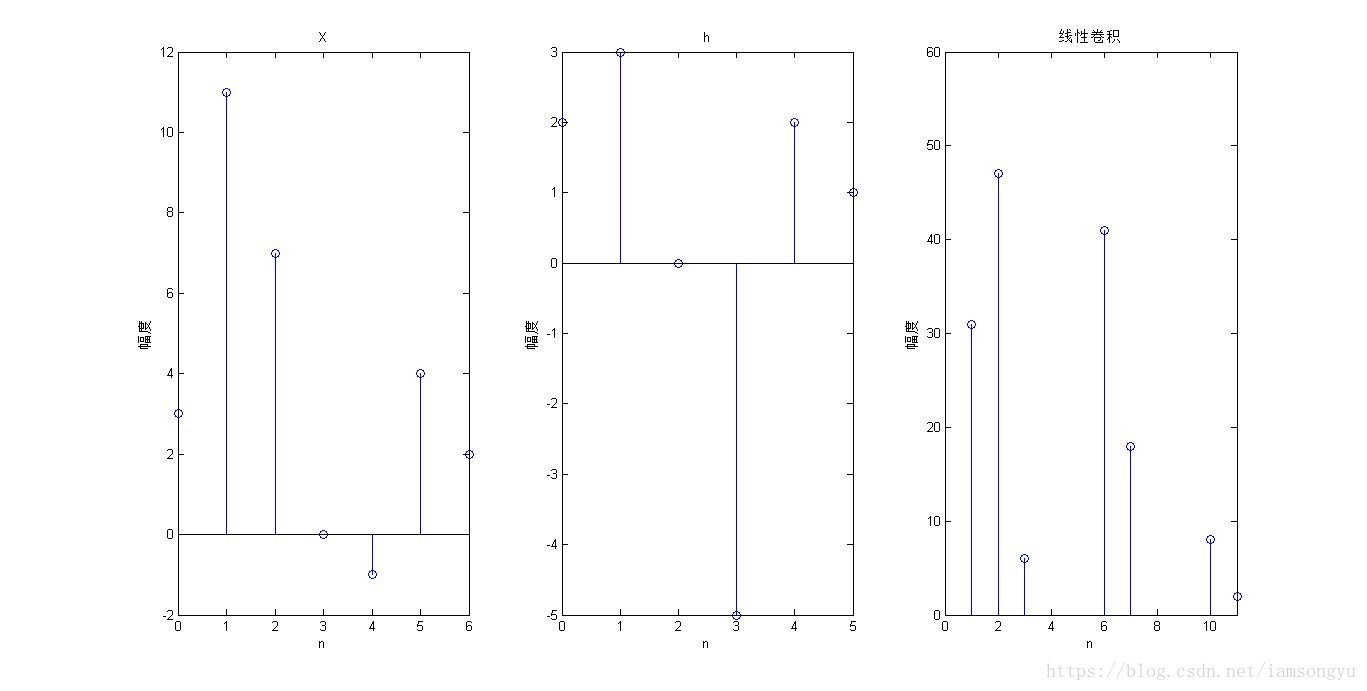
b) 根据线性卷积的步骤计算。
实验源程序:
(a)
clc
clear all
x=[3,11,7,0,-1,4,2];
nx=[0:length(x)-1];
h=[2,3,0,-5,2,1];
nh=[0:length(h)-1];
y=conv(x,h);
ny=[0:1:length(y)-1];
subplot(1,3,1)
stem(nx,x);
xlabel('n')
ylabel('幅度')
title('X')
subplot(1,3,2)
stem(nh,h)
xlabel('n')
ylabel('幅度')
title('h')
subplot(1,3,3)
stem(ny,y);
xlabel('n')
ylabel('幅度')
title('线性卷积')
clc
clear all
x=[3,11,7,0,-1,4,2];
h=[2,3,0,-5,2,1];
x1=zeros(1,length(h)-1);
x2=zeros(1,length(h)-1);
x3=[x1 x x2]; %补零
nx=[0:length(x)-1];
h1=zeros(1,length(x)+(length(h)-2));
h2=[h h1];
nh=[0:length(h)-1]; %补零
y=[];i=1;
for j=0:1:16
M=j+2; a=0;
for t=1:1:M-1
a=a+x3(t)*h2(M-t);
end
y(i)=a;
i=i+1;
end
ny=[-(length(h)-1):1:length(y)-6];
subplot(1,3,1)
stem(nx,x);
xlabel('n')
ylabel('幅度')
title('X')
subplot(1,3,2)
stem(nh,h)
xlabel('n')
ylabel('幅度')
title('h')
subplot(1,3,3)
stem(ny,y);
xlabel('n')
ylabel('幅度')
title('线性卷积')
axis([0 length(h)+length(x)-2 0 60]) %去掉补位0
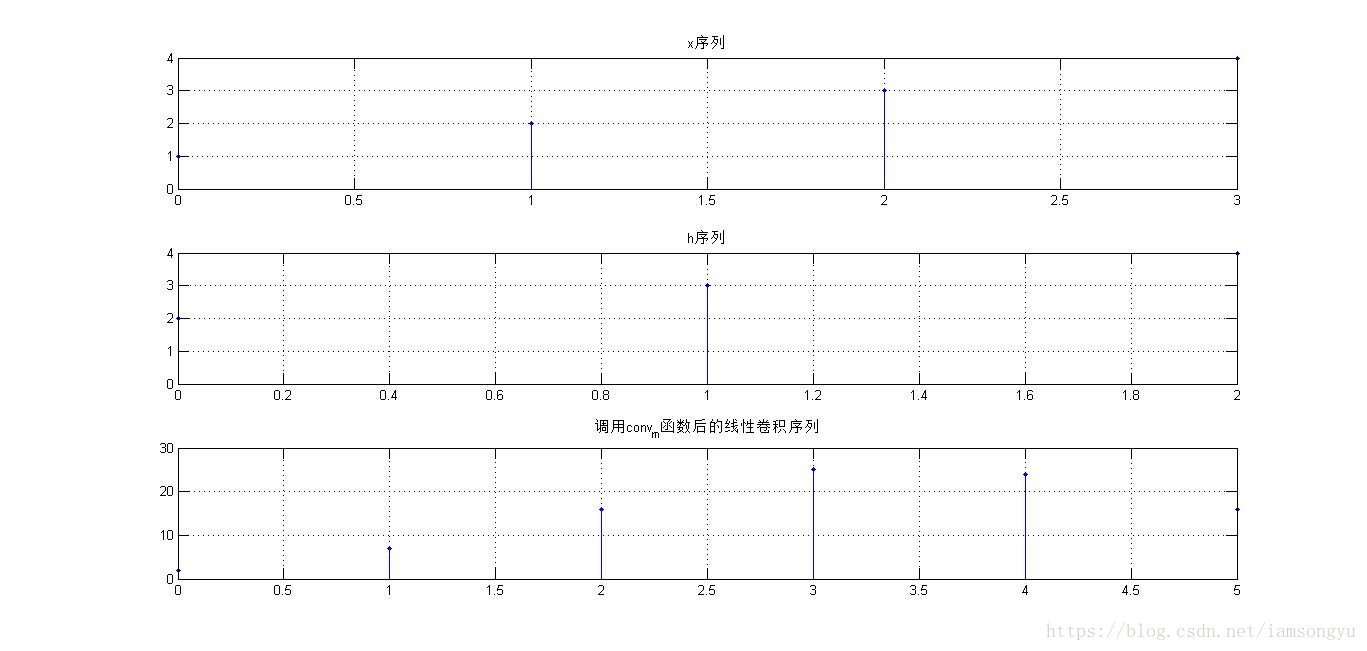
- 将函数conv稍加扩展为函数conv_m,它可以对任意基底的序列求卷积。格式如下:
function [y,ny]=conv_m(x,nx,h,nh)
% 信号处理的改进卷积程序
% [y,ny]=conv_m(x,nx,h,nh)
% [y,ny]=卷积结果
% [x,nx]=第一个信号
% [h,nh]=第二个信号
function [y,ny]=conv_m(x,nx,h,nh)
x=input('x=');
h=input('h=');
nx=length(x);
nh=length(h);
ny=nx+nh-1;
for(n=1:ny)
y(n)=0;
for(m=1:nh)
k=n-m+1;
if(k>=1&k<=nx)
y(n)=y(n)+h(m)*x(k);
end;
end;
end;
n=0:1:ny-1;
xx=0:nx-1;
hh=0:nh-1;
subplot(311);
stem(xx,x,'.');
title('x序列');
grid;
subplot(312);
stem(hh,h,'.');
title('h序列');
grid;
subplot(313);
stem(n,y,'.');
title('调用conv_m函数后的线性卷积序列');
grid;
end
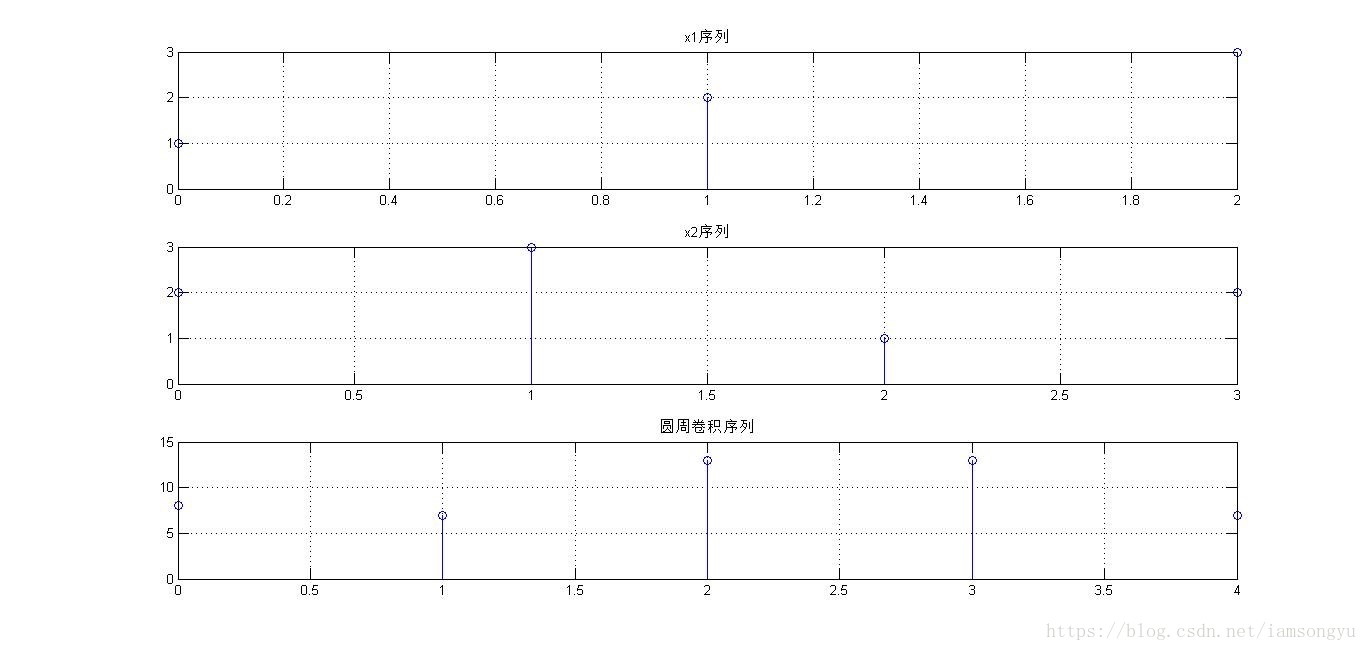
3. 创建函数circonv,来实现序列的圆周卷积,格式如下:
function y=circonv(x1,x2,N)
function y=circonv(x1,x2,N)
x1=input('x1=');
x2=input('x2=');
N=input('N=');
nx1=0:length(x1)-1;
nx2=0:length(x2)-1;
x_1=[x1 zeros(1,N-length(x1))];
h_1=[x2 zeros(1,N-length(x2))];
y1=conv(x_1,h_1);
z_1=[zeros(1,N) y1(1:(N-1))];
z_2=[y1((N+1):(2*N-1)) zeros(1,N)];
z=z_1(1:(2*N-1))+z_2(1:(2*N-1))+y1(1:(2*N-1));
y=z(1:N);
ny=0:N-1;
subplot(311);
stem(nx1,x1);
title('x1序列');
grid;
subplot(312);
stem(nx2,x2);
title('x2序列');
grid;
subplot(313);
stem(ny,y);
title('圆周卷积序列');
grid;
end
function y=circonv(x1,x2,N)
x_1=[x1 zeros(1,N-length(x1))];
h_1=[x2 zeros(1,N-length(x2))];
y1=conv(x_1,h_1);
z_1=[zeros(1,N) y1(1:(N-1))];
z_2=[y1((N+1):(2*N-1)) zeros(1,N)];
z=z_1(1:(2*N-1))+z_2(1:(2*N-1))+y1(1:(2*N-1));
y=z(10:N+10);
end
函数调用求多点圆周卷积:
n=-5:50;
N0=56;
k=input('k=');
c=input('c=');
N=k*N0+c;
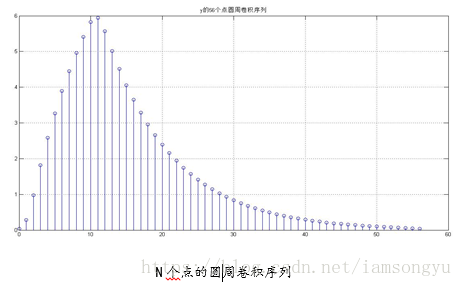
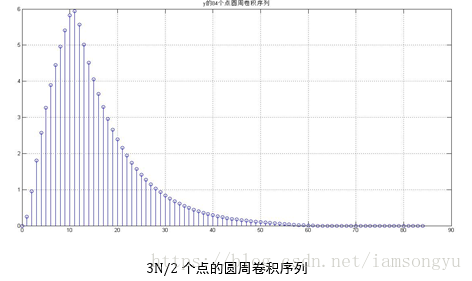
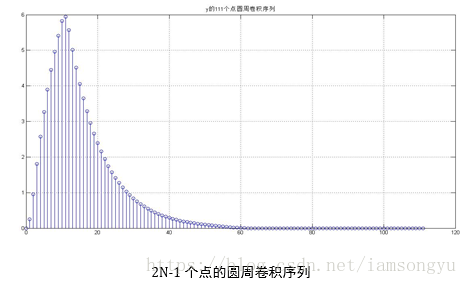
str =['y的',int2str(N),'个点圆周卷积序列']
xn=heaviside(n)-heaviside(n-10);
hn=0.9.^n.*heaviside(n);
y=circonv(xn,hn,N);
ny=[0:length(y)-1]
stem(ny,y);
title(str);
grid;
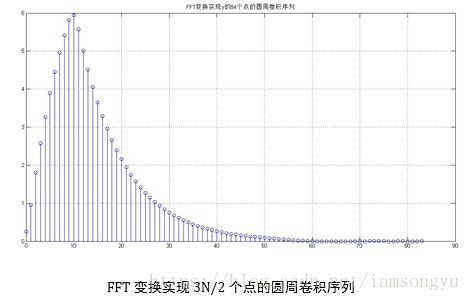
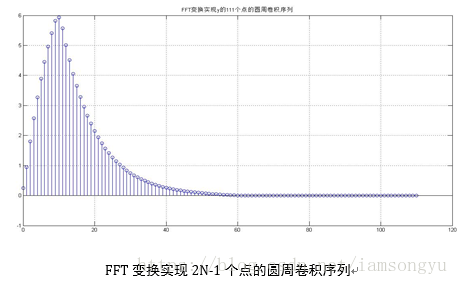
(2)FFT变换求圆周卷积
clc;
clear all;
n=-5:50;
N0=56;
k=input('k=');
c=input('c=');
N=k*N0+c;
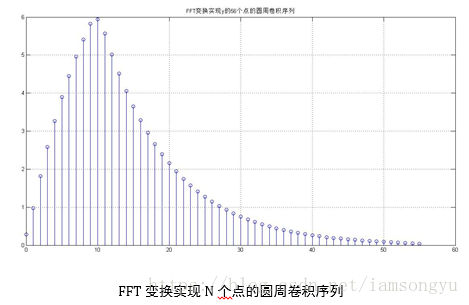
str =['FFT变换实现y的',int2str(N),'个点的圆周卷积序列']
x=heaviside(n)-heaviside(n-10);
h=0.9.^n.*heaviside(n);
X1=fft(x,N);
H1=fft(h,N);
Y1=X1.*H1;
y1=ifft(Y1,N);
stem((0:N-1),y1);
title(str);
grid;