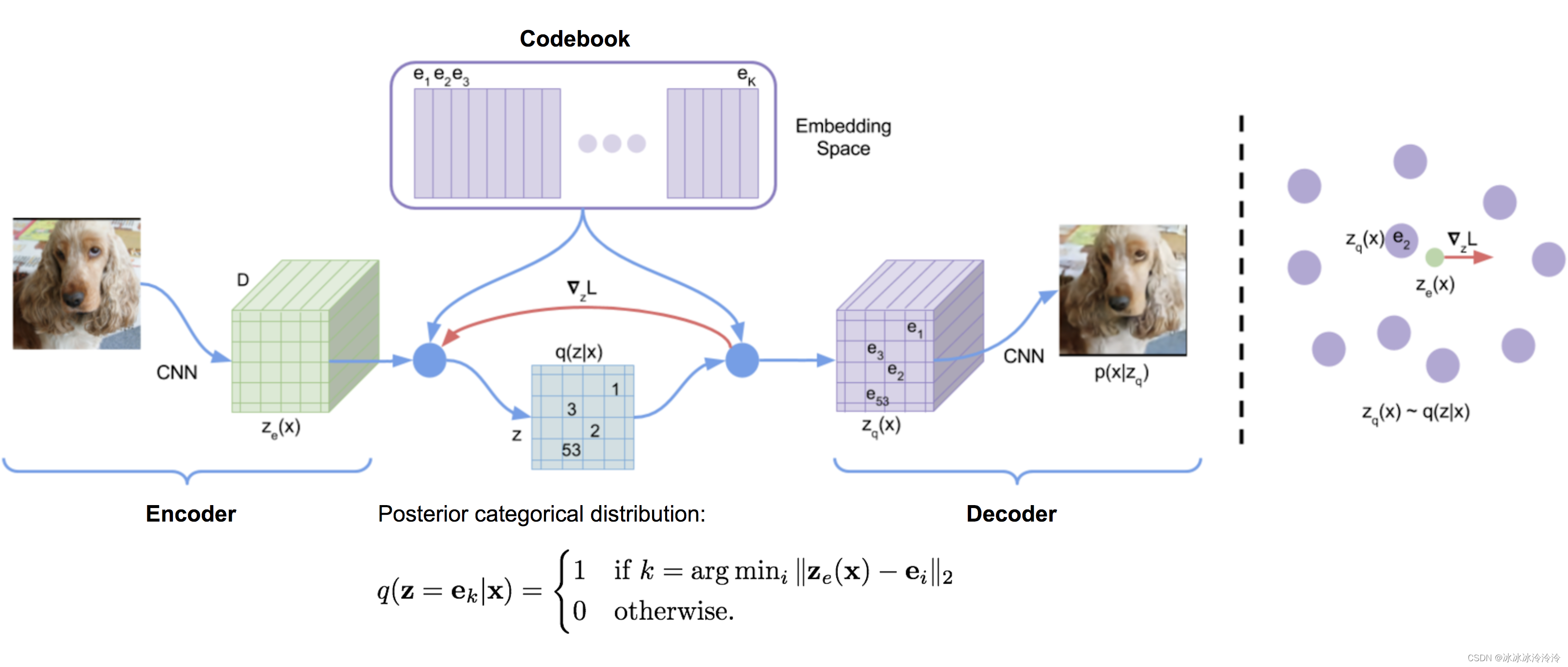
VQ-VAE
VAE(Variational AutoEncoder )是一种生成模型,VQ-VAE(Vector Quantised Variational AutoEncoder )是VAE的变种。
VAE的隐含变量是连续的,符合高斯分布,而VQ-VAE的隐含变量是离散的。离散的隐含变量对于自然语言,推理都比较有帮助。著名的DALL-E就使用了类似VQ-VAE的离散隐含变量来从文本生成图像。
VQ-VAE通过vector quantisation (VQ) 将隐含变量离散化。
假设
e
∈
R
K
×
D
\mathbf{e} \in \mathbb{R}^{K \times D}
e∈RK×D是codebook。其中
K
K
K是codebook中embeddings的个数,
D
D
D是embedding的维度。
e
i
\mathbf{e}_i
ei是其中一个embedding。
encoder的输出
E
(
x
)
=
z
e
E(\mathbf{x}) = \mathbf{z}_e
E(x)=ze将通过最近邻查找的方式找到自己属于的embedding向量
e
k
\mathbf{e}_k
ek:
z
q
(
x
)
=
Quantize
(
E
(
x
)
)
=
e
k
where
k
=
arg
min
i
∥
E
(
x
)
−
e
i
∥
2
\mathbf{z}_q(\mathbf{x}) = \text{Quantize}(E(\mathbf{x})) = \mathbf{e}_k \text{ where } k = \arg\min_i \|E(\mathbf{x}) - \mathbf{e}_i \|_2
zq(x)=Quantize(E(x))=ek where k=argimin∥E(x)−ei∥2并且要求embedding向量
e
k
\mathbf{e}_k
ek通过decoder
D
(
.
)
D(.)
D(.)的输出将尽可能与
x
\mathbf{x}
x相似。
于是有VQ-VAE的优化目标:
L
V
Q
V
A
E
=
∥
x
−
D
(
e
k
)
∥
2
2
⏟
reconstruction loss
+
∥
sg
[
E
(
x
)
]
−
e
k
∥
2
2
⏟
VQ loss
+
β
∥
E
(
x
)
−
sg
[
e
k
]
∥
2
2
⏟
commitment loss
L_{VQVAE} = \underbrace{\|\mathbf{x} - D(\mathbf{e}_k)\|_2^2}_{\textrm{reconstruction loss}} + \underbrace{\|\text{sg}[E(\mathbf{x})] - \mathbf{e}_k\|_2^2}_{\textrm{VQ loss}} + \underbrace{\beta \|E(\mathbf{x}) - \text{sg}[\mathbf{e}_k]\|_2^2}_{\textrm{commitment loss}}
LVQVAE=reconstruction loss
∥x−D(ek)∥22+VQ loss
∥sg[E(x)]−ek∥22+commitment loss
β∥E(x)−sg[ek]∥22其中sq表示stop_gradient。
普通VAE优化的目标是最小化负ELBO(即最大化ELBO):
L
V
A
E
=
−
E
z
∼
q
ϕ
(
z
∣
x
)
log
p
θ
(
x
∣
z
)
+
D
KL
(
q
ϕ
(
z
∣
x
)
∥
p
θ
(
z
)
)
L_{VAE}= -\mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z})+ D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}))
LVAE=−Ez∼qϕ(z∣x)logpθ(x∣z)+DKL(qϕ(z∣x)∥pθ(z))由于VQ-VAE假设先验
z
\mathbf z
z是均匀分布,
p
θ
(
z
)
=
1
K
{p_\theta(\mathbf z)}=\frac{1}{K}
pθ(z)=K1,
q
ϕ
(
z
∣
x
)
q_\phi(\mathbf{z}\vert\mathbf{x})
qϕ(z∣x)是中只有一维为1,其余为0。
D
KL
(
q
ϕ
(
z
∣
x
)
∥
p
θ
(
z
)
)
=
∑
z
q
ϕ
(
z
∣
x
)
ln
q
ϕ
(
z
∣
x
)
p
θ
(
z
)
=
E
q
ϕ
(
z
∣
x
)
ln
q
ϕ
(
z
∣
x
)
p
θ
(
z
)
=
E
q
ϕ
(
z
∣
x
)
ln
K
q
ϕ
(
z
∣
x
)
D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}))= \sum_\mathbf{z} q_\phi(\mathbf{z}\vert\mathbf{x}) \ln \frac{q_\phi(\mathbf{z}\vert\mathbf{x})}{p_\theta(\mathbf{z})}= \mathbb E_{q_\phi(\mathbf{z}\vert\mathbf{x})} \ln \frac{q_\phi(\mathbf{z}\vert\mathbf{x})}{p_\theta(\mathbf{z})}= \mathbb E_{q_\phi(\mathbf{z}\vert\mathbf{x})} \ln K q_\phi(\mathbf{z}\vert\mathbf{x})
DKL(qϕ(z∣x)∥pθ(z))=z∑qϕ(z∣x)lnpθ(z)qϕ(z∣x)=Eqϕ(z∣x)lnpθ(z)qϕ(z∣x)=Eqϕ(z∣x)lnKqϕ(z∣x)ELBO中的KL散度项是常数,因此KL散度项在训练时可以忽略。
为了使用batch的方式更新codebook,codebook中的embedding向量使用EMA (exponential moving average)学习:
N
i
(
t
)
=
γ
N
i
(
t
−
1
)
+
(
1
−
γ
)
n
i
(
t
)
m
i
(
t
)
=
γ
m
i
(
t
−
1
)
+
(
1
−
γ
)
∑
j
=
1
n
i
(
t
)
z
i
,
j
(
t
)
e
i
(
t
)
=
m
i
(
t
)
/
N
i
(
t
)
N_i^{(t)} = \gamma N_i^{(t-1)} + (1-\gamma)n_i^{(t)}\;\;\; \mathbf{m}_i^{(t)} = \gamma \mathbf{m}_i^{(t-1)} + (1-\gamma)\sum_{j=1}^{n_i^{(t)}}\mathbf{z}_{i,j}^{(t)}\;\;\; \mathbf{e}_i^{(t)} = \mathbf{m}_i^{(t)} / N_i^{(t)}
Ni(t)=γNi(t−1)+(1−γ)ni(t)mi(t)=γmi(t−1)+(1−γ)j=1∑ni(t)zi,j(t)ei(t)=mi(t)/Ni(t)其中
γ
∈
(
0
,
1
)
\gamma\in(0,1)
γ∈(0,1),
n
i
(
t
)
n_i^{(t)}
ni(t)是第t个batch中属于
e
i
\mathbf e_i
ei的数量(最近邻选择的是
e
i
\mathbf e_i
ei),
N
i
(
t
)
N_i^{(t)}
Ni(t)是第t次更新时属于
e
i
\mathbf e_i
ei的累计计数,
m
i
(
t
)
\mathbf{m}_i^{(t)}
mi(t)是第t次更新时属于
e
i
\mathbf e_i
ei的累计向量。
图像生成
一幅图像并不是经过编码器变为一个
D
D
D维的embedding,而是用卷积编码为
m
×
m
m\times m
m×m个
D
D
D维的embedding。这样可以保留图像的空间结构,并且用小的码本表示大量多变的图像。每个embedding对应于codebook中的一个位置,所以图像可以表示为
m
×
m
m\times m
m×m的整数矩阵,这就实现了图像的离散编码。
训练过程中,隐含表示
z
\mathbf z
z的服从均匀分布。在训练后,作者使用了自回归的方式拟合
m
×
m
m\times m
m×m个
z
\mathbf z
z。这样这些embedding之间是存在关系的,而不是独立的。具体地,作者对图像生成任务使用PixelCNN来生成隐含表示。
有点LDMs(Latent Diffusion Models)的感觉,隐含表示用PixelCNN生成,编码器和解码器用VQ-VAE。而LDMs则是隐含表示用diffusion model生成,编码器解码器用VAE。
参考
lilianweng.github.io VQ-VAE
https://www.spaces.ac.cn/archives/6760