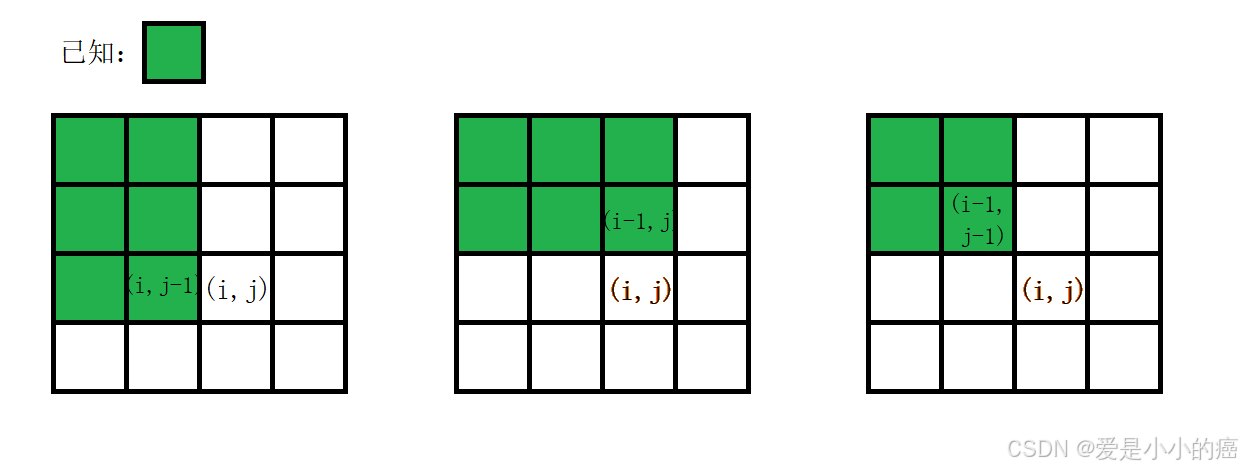(以下知识需要大家学习过一维前缀和与一维差分后再进行学习~)
(上篇文章:Java算法-一维前缀和与差分-CSDN博客)
一、二维前缀和
① 什么是二维前缀和?
我们已经学习过一维前缀和,所以通过"前缀和"三个字就能知道,其主要的作用肯定也还是:
"存储当前元素及其之前元素的和"
📚 二维前缀和的定义:
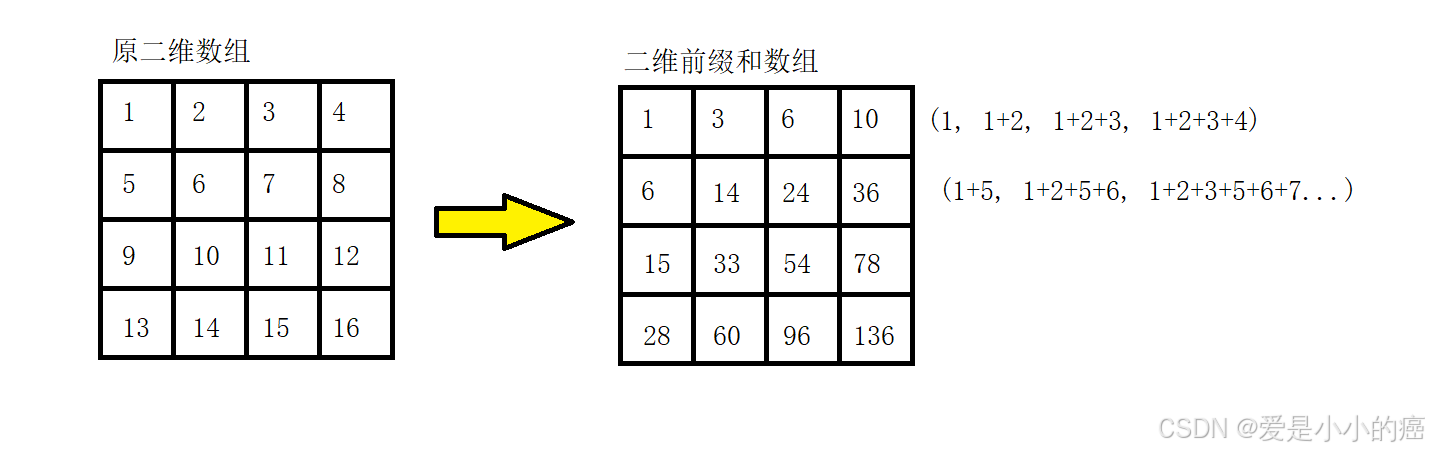
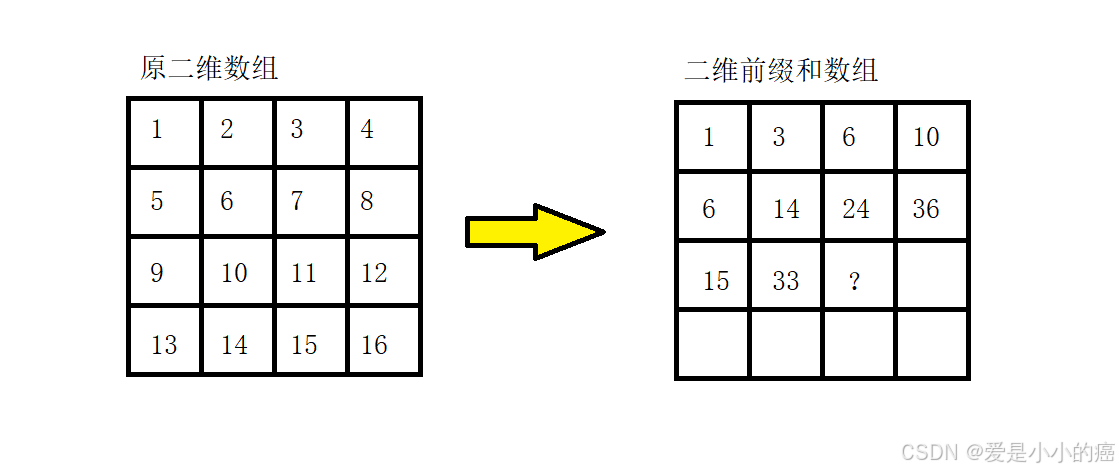
二维前缀和是指,在二维矩阵或二维数组中,以每个元素作为右下角的子矩阵或子数组,而该元素则代表这个子矩阵或子数组的和。
还是像之前一样,我们通过画图的展示方法来便于大家理解:
而这种二维前缀和一般又应用在何种地方呢?让我们看一道例题:
📖 给定一个 n * m 大小的矩阵 A,给定 q 组查询:
"每次查询给定4个正整数,x1,y1,x2,y2,你需要输出的值"
同样的,让我们考虑一下,在学习"二维前缀和"前的暴力解法:
(如果使用暴力解法,也就是通过"暴力枚举"全部遍历的方式进行求和的操作)
假设最坏的情况,每次查询都对矩阵的 n * m 个元素全部遍历:
那么我们的时间复杂度就应该是O(nmq),10^3 * 10^3 * 10^5,达到了1e11!
这也远远大于2e8,所以肯定是会超时的:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int q = scan.nextInt();
int[][] a = new int[n+1][m + 1];
int[][] s = new int[n+1][m + 1];
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
a[i][j] = scan.nextInt();
}
}
while(q-- > 0){
int x1 = scan.nextInt();
int y1 = scan.nextInt();
int x2 = scan.nextInt();
int y2 = scan.nextInt();
long num = 0;
for(int i = x1;i <= x2;i++){
for(int j = y1;j <= y2;j++){
num += a[i][j];
}
}
System.out.println(num);
}
}
}
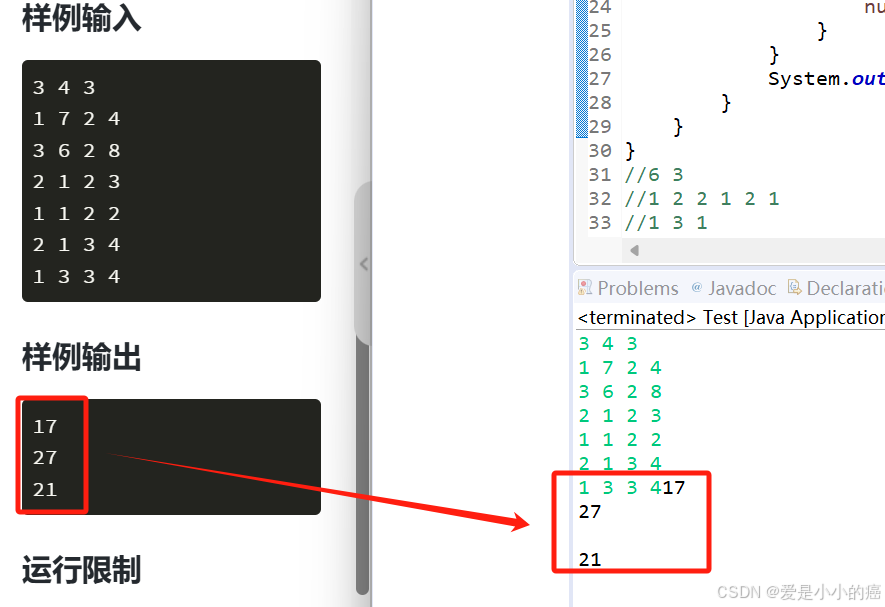
我们可以看到,通过这个样例是没有问题的,但是当我们提交检测时:
对的,果不其然的超时了。
② 二维前缀和的使用
那么此时,我们就可以使用二维前缀和来对这种代码进行一个优化。
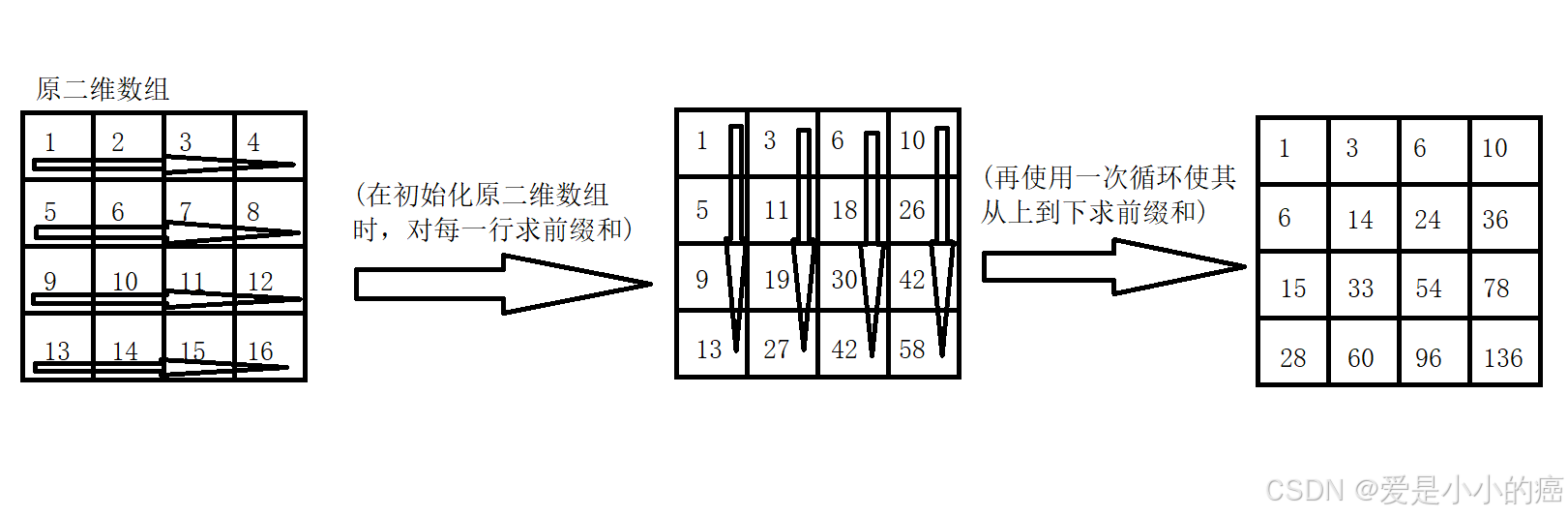
那么二维前缀和数组应该怎么求呢?当我们学习过一维前缀和后,或许有些聪明的小伙伴就会想到这样的方法:
其实这样的方法也能够有效的做到提高效率,但是我们要讲的最优解并非这种方法(但能想到这一步的小伙伴们已经很聪明啦~)
那么现在,假设我们已经找到了一个(可以在初始化原二维数组时,同时计算出二维前缀和数组的一个公式),并且算出了一部分的二维前缀和的元素:
那么由这个图片,我们来分析以下这个(神奇的公式)究竟是什么原理:
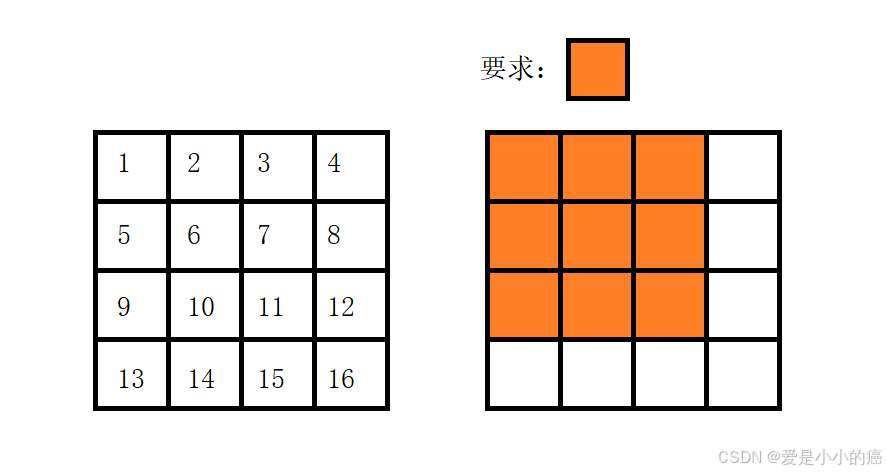
我们要求的 ' ? ' 位置代表 " 以该元素为右下角的子矩阵或子数组的和 ",故可以将其表示成这个图片,然后我们再来分析一下我们已有的数据:
如果我们将二维前缀和数组命名为" s " , 原数组命名为" a ",那么:
由图片我们可以看出,我们可以通过s[i,j-1] + s[i-1,j] - s[i-1,j-1] + a[i,j];就能够正好表示出s[i,j]~
📚 我们使用代码来试一下:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int[][] a = new int[n + 1][m + 1];
int[][] s = new int[n + 1][m + 1];
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
a[i][j] = scan.nextInt();
s[i][j] = a[i][j] + s[i-1][j] + s[i][j-1] - s[i-1][j-1];
}
}
System.out.println(Arrays.deepToString(a));
System.out.println(Arrays.deepToString(s));
}
}
成功的(在初始化原二维数组时,同时计算出二维前缀和数组)~
而求出了"二维前缀和数组"后,我们回到刚刚的问题:
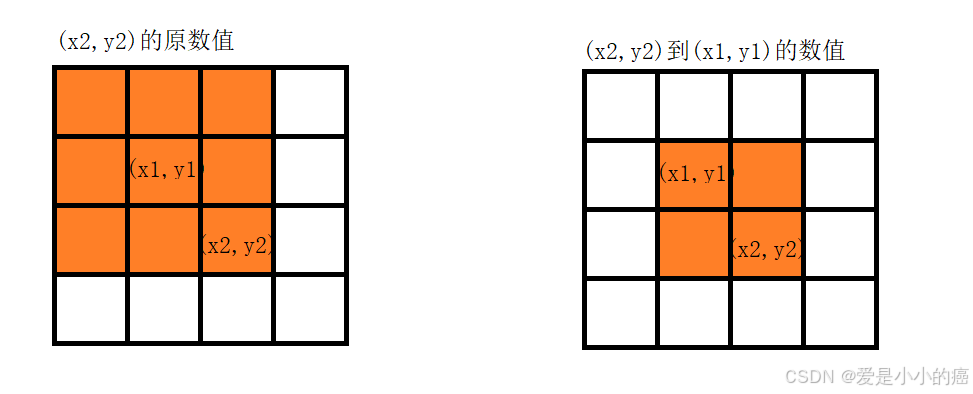
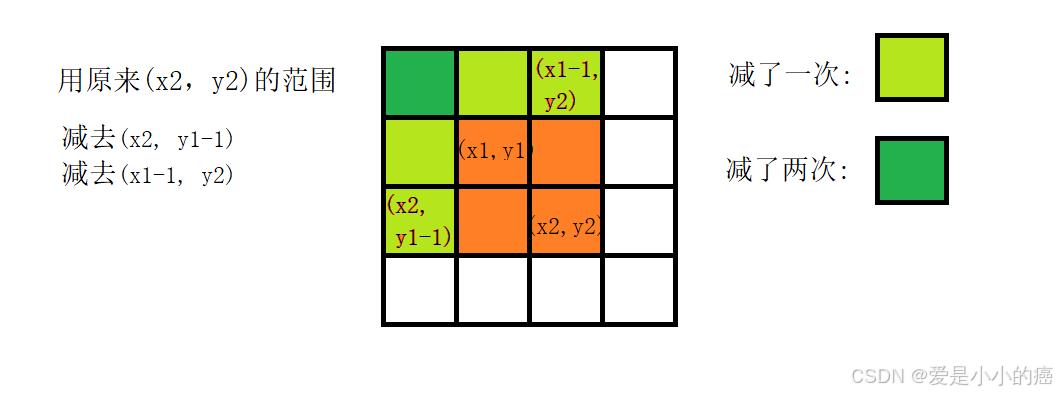
大概是求这样的范围:
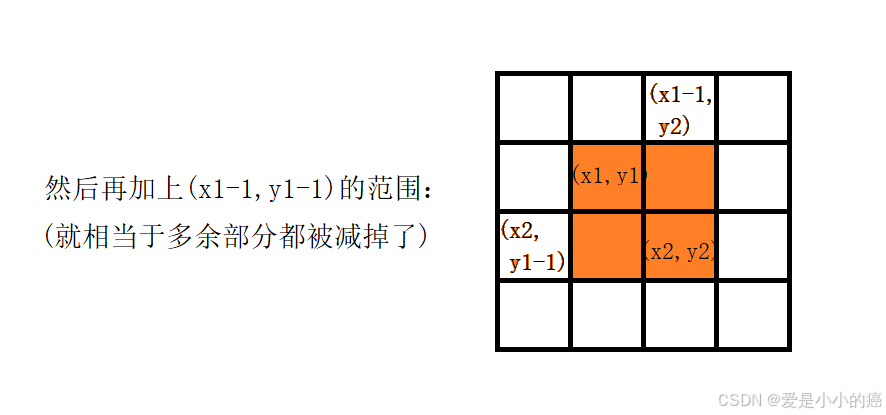
所以最后我们得到的 (x2,y2) 到 (x1,y1) 之间的范围和公式为:
s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1];
📚 接下来我们再去尝试是用公式去解刚刚的题:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int q = scan.nextInt();
int[][] a = new int[n + 5][m + 5];
int[][] s = new int[n + 5][m + 5];
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
a[i][j] = scan.nextInt();
s[i][j] = a[i][j] + s[i-1][j] + s[i][j-1] - s[i-1][j-1];
}
}
while(q-- > 0){
int x1 = scan.nextInt();
int y1 = scan.nextInt();
int x2 = scan.nextInt();
int y2 = scan.nextInt();
System.out.println(s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1]);
}
}
}使用二维前缀和能将q次操作中的O(nm)减少到O(1),怎么样?是不是效率非~~~常的高呀。
优化后,也是成功的通过了。
小练习:闪耀的灯光(⭐⭐)
📖 问题描述:
将一个公园视作 n * m 个矩形区域所构成 , 每个区域都有一盏灯,初始亮度为a[i][j];
现可以选择一个大的矩形区域,并按下开关一次,这将使得该区域内每盏灯的亮度减少 1,但每个区域内的灯的亮度最多只能减少至 a[i][j] - c,如果此时亮度为 a[i][j] - c,那么再次按下开关使得小灯亮度恢复至初始亮度。
现在将进行 t 次操作,每次操作会选择一个矩形区域,该区域左上角端点为(x1,y1),右下角端点为(x2,y2),然后将该区域内所有灯按下 k 次开关。在每次操作结束后,该区域内所有灯的总亮度是多少?
(在下一次操作前,他会将公园内 所有灯光恢复初始值。)
📚 思路提示:
📕 灯的亮度最多只能减少至 a[i][j] - c 再按就会恢复初始亮度
(当按c次时,亮度减少到最低,按(c+1)次时,亮度恢复,于是我们可以对操作数t对(c+1)取余)
📕 二维前缀和数组可能比较大,我们采用long来接收~
📕 想要求每次操作区域内亮度的变化,我们只需要求出(操作修改的亮度 * 此区域内的灯数)就ok
(区域内的灯数为:(x2 - x1 + 1) * (y2 - y1 + 1) 而非 (x2 - x) * (y2 - y1))
📚 代码实现:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int c = scan.nextInt();
//初始数组
int[][] a = new int[n + 5][m + 5];
//二维前缀和数组
long[][] s = new long[n + 5][m + 5];
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
a[i][j] = scan.nextInt();
s[i][j] = a[i][j] + s[i-1][j] + s[i][j-1] - s[i-1][j-1];
}
}
//t次操作
int t = scan.nextInt();
while(t-- > 0){
//操作后的整体亮度
long num = 0;
//该区域内减少的亮度
long sub = 0;
int x1 = scan.nextInt();
int y1 = scan.nextInt();
int x2 = scan.nextInt();
int y2 = scan.nextInt();
int k = scan.nextInt();
//当按c次时,亮度减少到最低,按(c+1)次时,亮度恢复
k %= (c + 1);
sub = ((long)(x2 - x1 + 1) *(y2 - y1 + 1) * k);
num = s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1] - sub;
System.out.println(num);
}
}
}
其实这题就是用了一个二维前缀和的框架,只要仔细读明白题中的注意点,还是不算难的~
二、二维差分
① 什么是二维差分?
📚 熟悉过一维差分后,对于二维差分,我们应该能大致猜出它的意思:
二维差分是指对于一个二维矩阵或二维数组,通过计算相邻元素之间的差值得到一个新的二维矩阵或数组。
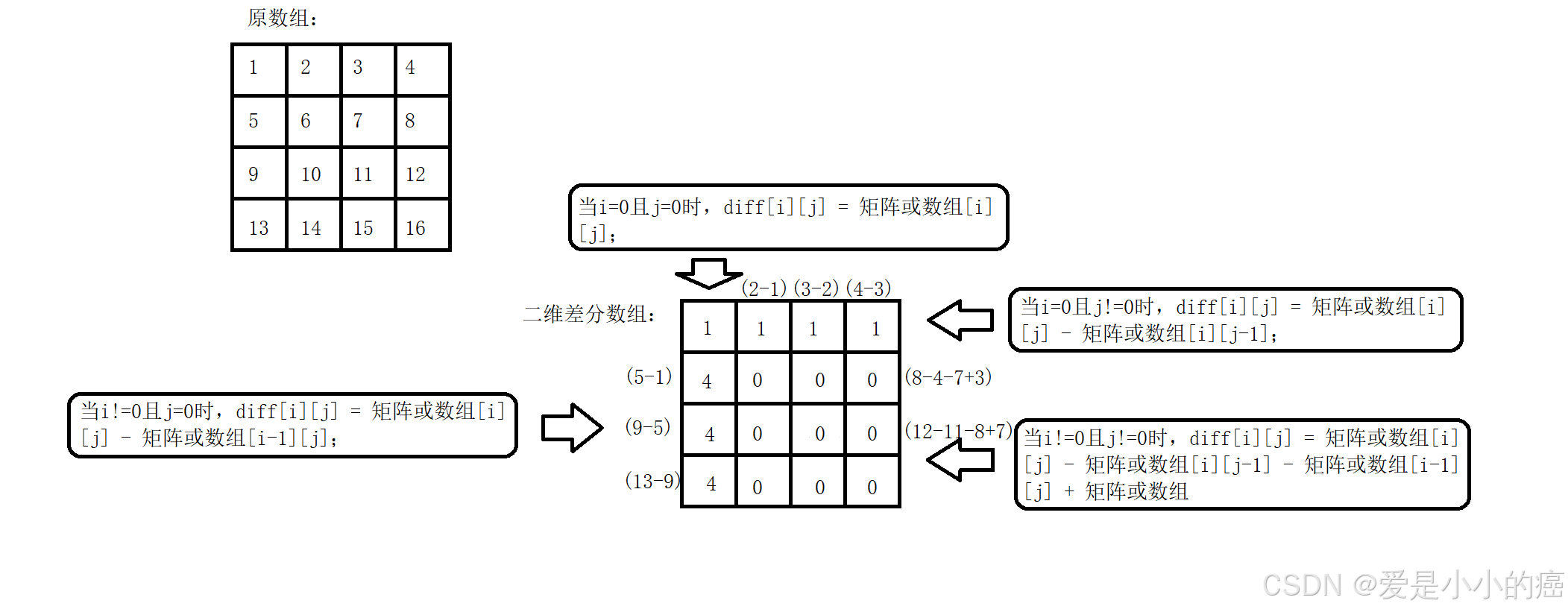
📖 二位差分数组的运算规则:
当i=0且j=0时,diff[i][j] = 矩阵或数组[i][j];
当i=0且j!=0时,diff[i][j] = 矩阵或数组[i][j] - 矩阵或数组[i][j-1];
当i!=0且j=0时,diff[i][j] = 矩阵或数组[i][j] - 矩阵或数组[i-1][j];
当i!=0且j!=0时,diff[i][j] = 矩阵或数组[i][j] - 矩阵或数组[i][j-1] - 矩阵或数组[i-1][j] + 矩阵或数组[i-1][j-1]。
还是一样的,我们来用图表述一下:
📚 接下来让我们看一道例题:
给定一个 n * m 大小的矩阵A,给定 q 组操作:
"每次操作为给定 5 个正整数:x1,y1,x2,y2,d。"
A(x1,y1)是子矩阵左上角端点,A(x2,y2)是子矩阵右下角端点,你需要给其中每个元素都 + d。
输出操作结束后的矩阵 A。
让我们看看使用暴力做法:枚举每个(x2,y2)到(x1,y1)的矩阵:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int q = scan.nextInt();
int[][] a = new int[n+1][m+1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] = scan.nextInt();
}
}
while(q-- > 0){
int x1 = scan.nextInt();
int y1 = scan.nextInt();
int x2 = scan.nextInt();
int y2 = scan.nextInt();
int d = scan.nextInt();
for (int i = x1; i <= x2; i++) {
for (int j = y1; j <= y2; j++) {
a[i][j] += d;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
System.out.print(a[i][j] + " ");
}
System.out.println();
}
}
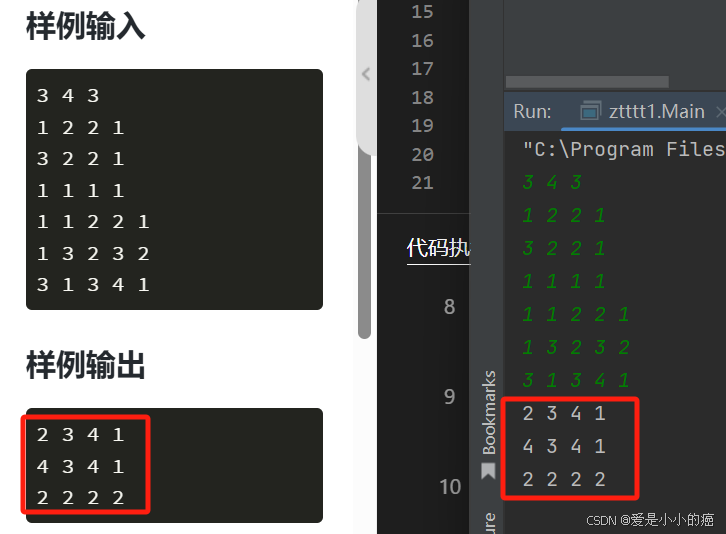
}虽然运算是没错的,但是还是会超时:
同样的,因为每次操作遍历枚举,可能会造成将整个数组都遍历,那么最坏的时间复杂度就是
O(qmn);(1e11 远大于 2e8)
② 二维差分的使用
那么接下来,让我们看看如何使用二维差分的方法去优化解题方法:
求二维差分数组:
请大家调动我们的逆向思维:在我们使用二维差分数组求前缀和时,得到的是原数组。
那我们反过来看,将式子反转,就能得到二维差分数组了:
a[i][j] = s[i][j] - s[i-1][j] - s[i][j-1] + s[i-1][j-1];
然后我们再看一下,如何修改二维差分数组:
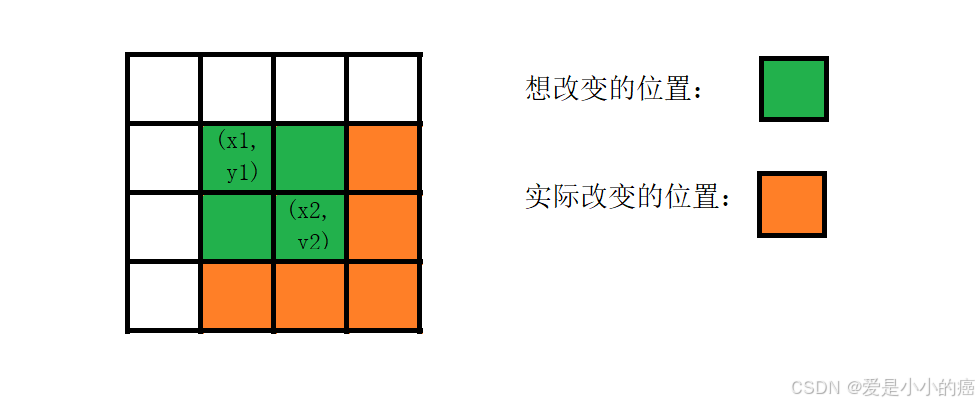
当我们直接对二维差分数组的端点(x1,y1)进行操作时:
而应该如何避免这种情况呢:
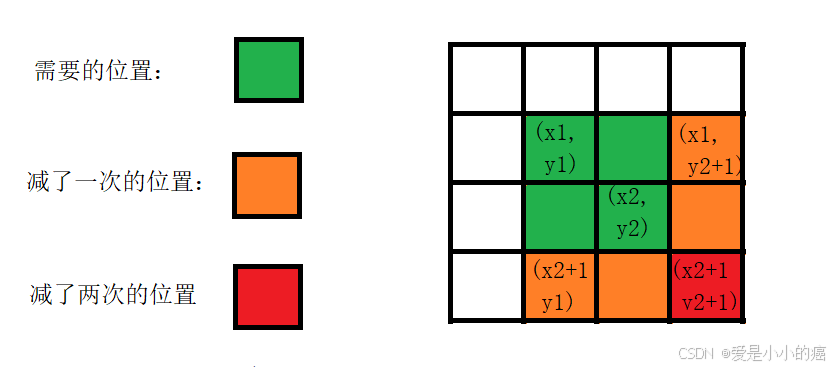
通过该图片,我们可以看出,想要让规定范围内的元素都加一个值,能得到如下的公式:
a[x1][y1] += c;
a[x2+1][y1] -= c;
a[x1][y2+1] -= c;
a[x2+1][y2+1] -= c;
📚 那么接下来让我们使用二维差分的知识来进行题解吧~:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int q = scan.nextInt();
int[][] a = new int[n+5][m+5];
int[][] s = new int[n+5][m+5];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] = scan.nextInt();
s[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1];
}
}
while(q-- > 0){
int x1 = scan.nextInt();
int y1 = scan.nextInt();
int x2 = scan.nextInt();
int y2 = scan.nextInt();
int d = scan.nextInt();
Donum(x1,y1,x2,y2,d,s);
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1];
System.out.print(s[i][j] + " ");
}
System.out.println();
}
}
public static void Donum(int x1,int y1,int x2,int y2,int d,int[][] arr){
arr[x1][y1] += d;
arr[x2+1][y1] -= d;
arr[x1][y2+1] -= d;
arr[x2+1][y2+1] += d;
}
}小练习:棋盘(⭐⭐)
📚 问题描述:
有一个 n * n 大小的棋盘,一开始棋盘上都是白子,当小蓝进行了 m 次操作后,每次操作会将棋盘上某个范围内的所有棋子的颜色取反(也就是白色棋子变为黑色,黑色棋子变为白色)。请输出所有操作做完后棋盘上每个棋子的颜色。
(输出格式:输出n行,每行n个0或1,表示该位置棋子颜色,0代表白,1代表黑)
📖 思路提示:
📕 首先我们需要注意,是n*n棋盘,m次操作。而不是n*m棋盘,q次操作;
📕 默认都是白子,则不用初始化,全为0即可,对进行操作的棋子++,最后%2即可;
📚 代码实现:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int[][] s = new int[n+5][n+5];
while(m-- > 0){
int x1 = scan.nextInt();
int y1 = scan.nextInt();
int x2 = scan.nextInt();
int y2 = scan.nextInt();
Donum(x1,y1,x2,y2,s);
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1];
System.out.print(s[i][j]%2);
}
System.out.println();
}
}
public static void Donum(int x1,int y1,int x2,int y2,int[][] arr){
arr[x1][y1] += 1;
arr[x2+1][y1] -= 1;
arr[x1][y2+1] -= 1;
arr[x2+1][y2+1] += 1;
}
}那么这次关于"二维前缀和"和"二维差分"的相关知识,就为大家分享到这里啦,如果有什么不懂的或者还可以改进的地方,请大家多多在评论区指出,我也会虚心改正的!那么我们下期再见啦~