Understanding the difficulty of training deep feedforward neural networks by Xavier Glorot, Yoshua Bengio in AISTATS 2010.
本文介绍一下深度学习参数初始化问题中耳熟能详的参数初始化方法——Xavier(发音[‘zeɪvɪr])初始化。
大家应该感觉到一般的深度学习文章上来就是实验,告诉读者这个实验结果好,然后由实验结果再反向给出一些无从验证的可能对可能不对的原因。而这篇文章虽然整体来看比较简单,但结构非常严谨:首先通过实验分析标准初始化方法的问题;然后根据两个目标——状态方差和梯度方差保持不变推导出参数的特点,给出Xavier初始化方法的具体形式;最后通过实验验证Xavier初始化的效果确实不错。
在开始阅读下面的内容之前,我们需要牢记参数初始化的目的是为了让神经网络在训练过程中学习到有用的信息,这意味着参数梯度不应该为0。而我们知道在全连接的神经网络中,参数梯度和反向传播得到的状态梯度以及入激活值有关——激活值饱和会导致该层状态梯度信息为0,然后导致下面所有层的参数梯度为0;入激活值为0会导致对应参数梯度为0。所以如果要保证参数梯度不等于0,那么参数初始化应该使得各层激活值不会出现饱和现象且激活值不为0。我们把这两个条件总结为参数初始化条件:
- 初始化必要条件一:各层激活值不会出现饱和现象。
- 初始化必要条件二:各层激活值不为0。
需要说明的是这篇论文只研究了解决分类问题的5层的全连接神经网络,每个隐层的神经元个数为1000,并且仅探讨了三种激活函数:sigmoid、tanh、softsign。
标准初始化方法
形式
把权重矩阵初始化为如下形式: W i j ∼ U [ − 1 n , 1 n ] W_{i j} \sim U\left[-\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}\right] Wij∼U[−n1,n1]其中 U [ − a , a ] U[−a,a] U[−a,a]是区间 ( − a , a ) (−a,a) (−a,a)上的均匀分布, n n n是入神经网络的大小。易知 Var ( W i j ) = 1 3 n \operatorname{Var}\left(W_{i j}\right)=\frac{1}{3 n} Var(Wij)=3n1在深入介绍标准初始化之前,首先给出随机变量方差的两个性质:
- 假设随机变量X和随机变量Y相互独立,则有 Var ( X + Y ) = Var ( X ) + Var ( Y ) \operatorname{Var}(X+Y)=\operatorname{Var}(X)+\operatorname{Var}(Y) Var(X+Y)=Var(X)+Var(Y)
- 假设随机变量X和随机变量Y相互独立,且E(X)=E(Y)=0,则有 Var ( X Y ) = Var ( X ) Var ( Y ) \operatorname{Var}(X Y)=\operatorname{Var}(X) \operatorname{Var}(Y) Var(XY)=Var(X)Var(Y)
神经网络的隐层状态计算表达式:
z
i
=
W
i
h
i
−
1
,
i
=
0
,
1
,
…
\mathbf{z}^{\mathbf{i}}=W^{i} \mathbf{h}^{\mathbf{i}-\mathbf{1}}, i=0,1, \ldots
zi=Wihi−1,i=0,1,…其中
h
0
=
x
\mathbf{h}^{0}=\mathbf{x}
h0=x激活值计算表达式:
h
i
=
f
(
z
i
)
,
i
=
1
,
2
,
…
\mathbf{h}^{\mathbf{i}}=f\left(\mathbf{z}^{i}\right), i=1,2, \ldots
hi=f(zi),i=1,2,…论文中的符号和我的有些区别:论文中用
z
z
z表示激活值,
s
s
s表示状态值。我这里按自己的习惯来写。
现在把输入
x
x
x的每一维度
x
x
x看做一个随机变量,并且假设
E
(
x
)
=
0
E(x)=0
E(x)=0,
V
a
r
(
x
)
=
1
Var(x)=1
Var(x)=1。假设
W
W
W和
x
x
x相互独立,则隐层状态的方差为
Var
(
z
k
)
=
Var
(
∑
i
=
0
n
W
k
i
x
i
)
=
∑
i
=
0
n
Var
(
W
k
i
)
Var
(
x
i
)
=
∑
i
=
0
n
Var
(
W
k
i
)
=
∑
i
=
0
n
1
3
n
=
1
3
\begin{aligned} \operatorname{Var}\left(z_{k}\right) &=\operatorname{Var}\left(\sum_{i=0}^{n} W_{k i} x_{i}\right) \\ &=\sum_{i=0}^{n} \operatorname{Var}\left(W_{k i}\right) \operatorname{Var}\left(x_{i}\right) \\ &=\sum_{i=0}^{n} \operatorname{Var}\left(W_{k i}\right) \\ &=\sum_{i=0}^{n} \frac{1}{3 n} \\ &=\frac{1}{3} \end{aligned}
Var(zk)=Var(i=0∑nWkixi)=i=0∑nVar(Wki)Var(xi)=i=0∑nVar(Wki)=i=0∑n3n1=31可以看出标准初始化方法得到一个非常好的特性:隐层的状态的均值为0,方差为常量
1
3
\frac{1}{3}
31,和网络的层数无关,这意味着对于sigmoid函数来说,自变量落在有梯度的范围内。
但是因为sigmoid激活值都是大于0的,会导致下一层的输入不满足
E
(
⋅
)
=
0
E(\cdot)=0
E(⋅)=0。其实标准初始化也只适用于满足下面将要提到的Glorot假设的激活函数,比如tanh。
激活值和梯度特性实验
初始化后的激活值和梯度特性
首先下面以tanh神经网络为例,查看激活值和梯度的分布情况。
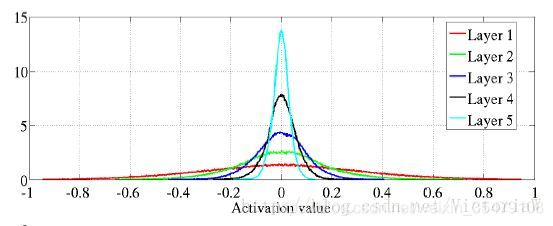
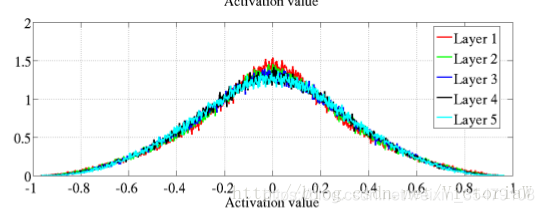
- 各层激活值直方图如下:
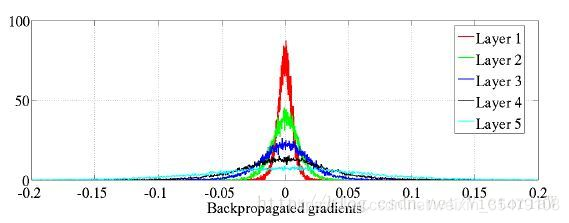
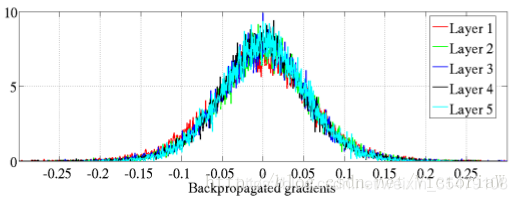
可以看出,激活值的方差逐层递减,这可以通过把公式(2)带入公式(15)进行解释。 - 各层反向传播的梯度(关于状态的梯度)的分布情况:
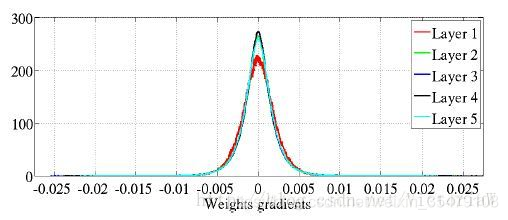
状态的梯度在反向传播过程中越往下梯度越小(因为方差越来越小)。这可以用公式(2)代入(16)进行解释。 - 各层参数梯度的分布情况
参数梯度的方差和层数基本无关,这可以通过公式公式(2)代入(17)进行解释。另外这幅图应该和后面会出现的Xavier初始化对应的图作比较,会发现各层的标准初始化参数梯度小了一个数量级,可以通过公式(2)(20)和公式(17)进行解释。
训练过程中的激活值特性
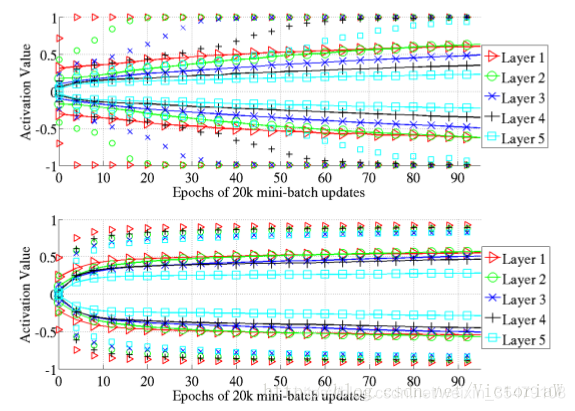
作者探究了三种激活函数对应的神经网络在训练过程中各层激活值的分布情况,得到下面的结果图。
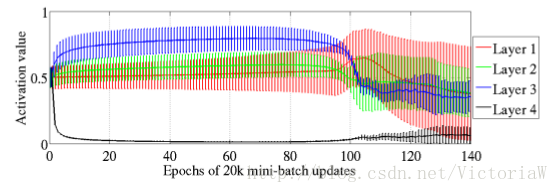
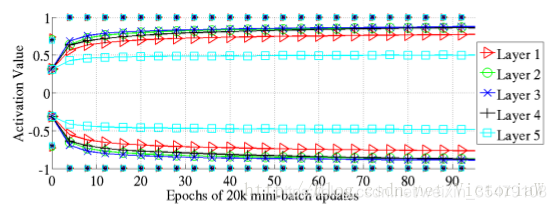
- sigmoid神经网络在每层的激活值均值和标准偏差在训练过程中的演变情况
这幅图比较有意思的是Layer 4的激活值在训练开始没多久就变成0(均值为0并且方差为0说明大多数激活值都为0),即进入饱和状态;而在最后又慢慢跳出饱和状态。
为什么会出现这种现象呢?读者可以自己想一想。在原论文中有作者给的解释。 - tanh神经网络和sofsign神经网络在训练过程中每层激活值的分布情况
可以看到在tanh神经网络中第一层最先饱和,然后是后面各层按顺序出现饱和。softsign神经网络中饱和现象并不严重,而且各层差不多同时出现饱和情况。
作者提到出现这种现象的原因有待于探究。
训练完成后的激活值特性
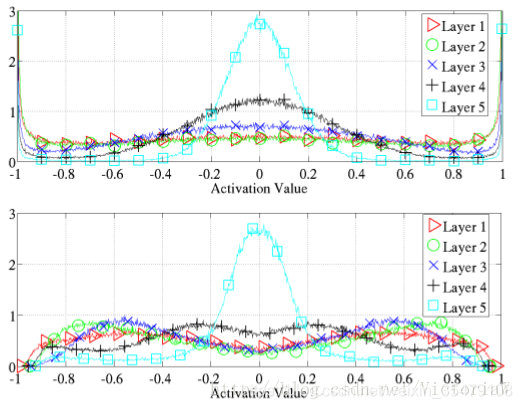
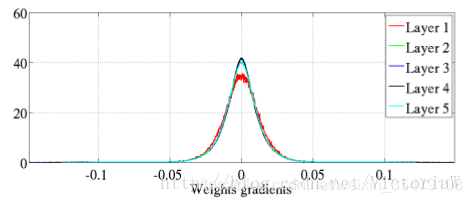
- 训练完成后tanh神经网络和softsign神经网络各层的激活值的直方图
tanh神经网络的低层出现了饱和现象:-1和1对应的神经元非常多。
Xavier初始化
在文章开始部分我们给出了参数初始化的必要条件。但是这两个条件只保证了训练过程中可以学到有用的信息——参数梯度不为0。而Glorot认为:优秀的初始化应该使得各层的激活值和状态梯度的方差在传播过程中的方差保持一致:
∀
(
i
,
j
)
,
Var
(
h
i
)
=
Var
(
h
j
)
∀
(
i
,
j
)
,
Var
(
∂
cos
t
∂
z
i
)
=
Var
(
∂
cos
t
∂
z
j
)
\begin{aligned} \forall(i, j), \operatorname{Var}\left(h^{i}\right) &=\operatorname{Var}\left(h^{j}\right) \\ \forall(i, j), \operatorname{Var}\left(\frac{\partial \cos t}{\partial z^{i}}\right) &=\operatorname{Var}\left(\frac{\partial \cos t}{\partial z^{j}}\right) \end{aligned}
∀(i,j),Var(hi)∀(i,j),Var(∂zi∂cost)=Var(hj)=Var(∂zj∂cost)
我们把这两个条件称为Glorot条件。
形式
在某些假设下反向传播梯度和参数梯度表达式
首先给出关于状态的梯度和关于参数的梯度的表达式:
∂
cos
t
∂
z
k
i
=
f
′
(
z
k
i
)
(
W
,
,
k
i
+
1
)
T
∂
cos
t
∂
z
i
+
1
\frac{\partial \cos t}{\partial z_{k}^{i}}=f \prime\left(z_{k}^{i}\right)\left(W_{,, k}^{i+1}\right)^{T} \frac{\partial \cos t}{\partial \mathbf{z}^{i+1}}
∂zki∂cost=f′(zki)(W,,ki+1)T∂zi+1∂cost
∂
C
o
s
t
∂
w
l
,
k
i
=
h
l
i
−
1
∂
cos
t
∂
z
k
i
\frac{\partial C o s t}{\partial w_{l, k}^{i}}=h_{l}^{i-1} \frac{\partial \cos t}{\partial z_{k}^{i}}
∂wl,ki∂Cost=hli−1∂zki∂cost我们做如下假设:
- 输入的每个特征方差一样: V a r ( x ) Var(x) Var(x);
- 激活函数对称:这样就可以假设每层的输入均值都是0;
- f ′ ( 0 ) = 1 f′(0)=1 f′(0)=1;
- 初始时,状态值落在激活函数的线性区域: f ′ ( s k i ) ≈ 1 f \prime\left(s_{k}^{i}\right) \approx 1 f′(ski)≈1。
后三个都是关于激活函数的假设,我们称为Glorot激活函数假设。
于是:
Var
(
h
l
i
)
=
Var
(
f
(
z
l
i
)
)
=
Var
(
z
l
i
)
=
Var
(
∑
k
=
1
n
i
−
1
W
l
k
i
h
k
i
−
1
)
=
∑
k
=
1
n
i
−
1
Var
(
W
l
k
i
h
k
i
−
1
)
=
n
i
−
1
Var
(
W
l
k
i
)
Var
(
h
i
−
1
)
=
n
i
−
1
Var
(
W
i
)
Var
(
h
i
−
1
)
=
Var
(
x
)
∏
i
′
=
1
i
n
i
′
−
1
Var
(
W
i
′
)
\begin{aligned} \operatorname{Var}\left(h_{l}^{i}\right) &=\operatorname{Var}\left(f\left(z_{l}^{i}\right)\right) \\ &=\operatorname{Var}\left(z_{l}^{i}\right) \\ &=\operatorname{Var}\left(\sum_{k=1}^{n_{i-1}} W_{l k}^{i} h_{k}^{i-1}\right) \\ &=\sum_{k=1}^{n_{i-1}} \operatorname{Var}\left(W_{l k}^{i} h_{k}^{i-1}\right) \\ &=n_{i-1} \operatorname{Var}\left(W_{l k}^{i}\right) \operatorname{Var}\left(h^{i-1}\right) \\ &=n_{i-1} \operatorname{Var}\left(W^{i}\right) \operatorname{Var}\left(h^{i-1}\right) \\ &=\operatorname{Var}(x) \prod_{i'=1}^{i} n_{i'-1} \operatorname{Var}\left(W^{i'}\right) \end{aligned}
Var(hli)=Var(f(zli))=Var(zli)=Var(k=1∑ni−1Wlkihki−1)=k=1∑ni−1Var(Wlkihki−1)=ni−1Var(Wlki)Var(hi−1)=ni−1Var(Wi)Var(hi−1)=Var(x)i′=1∏ini′−1Var(Wi′)对于一个d层的网络,由公式(10)可以推出:
Var
(
∂
C
o
s
t
∂
z
i
)
=
Var
(
(
W
⋅
,
k
i
+
1
)
T
∂
cos
t
∂
z
i
+
1
)
=
Var
(
∑
j
=
1
n
i
+
1
W
i
+
1
∂
cos
t
∂
z
i
+
1
)
=
n
i
+
1
Var
(
W
i
+
1
∂
cos
t
∂
z
i
+
1
)
=
n
i
+
1
Var
(
W
i
+
1
)
Var
(
∂
C
o
s
t
∂
z
i
+
1
)
=
n
i
+
1
n
i
+
2
Var
(
W
i
+
1
)
Var
(
W
i
+
2
)
Var
(
∂
cos
t
∂
z
i
+
2
)
=
n
i
+
1
n
i
+
2
⋯
n
d
Var
(
W
i
+
1
)
Var
(
W
i
+
2
)
⋯
Var
(
W
d
)
Var
(
∂
cos
t
∂
z
d
)
=
Var
(
∂
cos
t
∂
z
d
)
∏
i
′
=
i
+
1
d
n
i
′
Var
(
W
i
′
)
\begin{aligned} \operatorname{Var}\left(\frac{\partial C o s t}{\partial z^{i}}\right) &=\operatorname{Var}\left(\left(W_{\cdot, k}^{i+1}\right)^{T} \frac{\partial \cos t}{\partial \mathbf{z}^{i+1}}\right) \\ &=\operatorname{Var}\left(\sum_{j=1}^{n_{i+1}} W^{i+1} \frac{\partial \cos t}{\partial z^{i+1}}\right) \\ &=n_{i+1} \operatorname{Var}\left(W^{i+1} \frac{\partial \cos t}{\partial z^{i+1}}\right) \\ &=n_{i+1} \operatorname{Var}\left(W^{i+1}\right) \operatorname{Var}\left(\frac{\partial C o s t}{\partial z^{i+1}}\right) \\& =n_{i+1} n_{i+2} \operatorname{Var}\left(W^{i+1}\right) \operatorname{Var}\left(W^{i+2}\right) \operatorname{Var}\left(\frac{\partial \cos t}{\partial z^{i+2}}\right) \\ &=n_{i+1} n_{i+2} \cdots n_{d} \operatorname{Var}\left(W^{i+1}\right) \operatorname{Var}\left(W^{i+2}\right) \cdots \operatorname{Var}\left(W^{d}\right) \operatorname{Var}\left(\frac{\partial \cos t}{\partial z^{d}}\right) \\ &=\operatorname{Var}\left(\frac{\partial \cos t}{\partial z^{d}}\right) \prod_{i'=i+1}^{d} n_{i'} \operatorname{Var}\left(W^{i'}\right) \end{aligned}
Var(∂zi∂Cost)=Var((W⋅,ki+1)T∂zi+1∂cost)=Var(j=1∑ni+1Wi+1∂zi+1∂cost)=ni+1Var(Wi+1∂zi+1∂cost)=ni+1Var(Wi+1)Var(∂zi+1∂Cost)=ni+1ni+2Var(Wi+1)Var(Wi+2)Var(∂zi+2∂cost)=ni+1ni+2⋯ndVar(Wi+1)Var(Wi+2)⋯Var(Wd)Var(∂zd∂cost)=Var(∂zd∂cost)i′=i+1∏dni′Var(Wi′)由公式(11)(12)(13)可以推出:
Var
(
∂
C
ost
∂
w
i
)
=
Var
(
h
i
−
1
)
⋅
Var
(
∂
cos
t
∂
z
i
)
=
Var
(
x
)
∏
i
′
=
1
i
−
1
n
i
′
−
1
Var
(
W
i
′
)
⋅
Var
(
∂
Cos
t
∂
z
d
)
∏
i
′
=
i
+
1
d
n
i
′
Var
(
W
i
′
)
=
Var
(
x
)
Var
(
∂
cost
∂
z
d
)
∏
i
′
=
1
i
−
1
n
i
′
−
1
Var
(
W
i
′
)
⋅
∏
i
′
=
i
+
1
d
n
i
′
,
Var
(
W
i
′
)
\begin{aligned} \operatorname{Var}\left(\frac{\partial C \text {ost}}{\partial w^{i}}\right)& =\operatorname{Var}\left(h^{i-1}\right) \cdot \operatorname{Var}\left(\frac{\partial \cos t}{\partial z^{i}}\right) \\ & =\operatorname{Var}(x) \prod_{i'=1}^{i-1} n_{i'-1} \operatorname{Var}\left(W^{i'}\right) \cdot \operatorname{Var}\left(\frac{\partial \operatorname{Cos} t}{\partial z^{d}}\right) \prod_{i'=i+1}^{d} n_{i'} \operatorname{Var}\left(W^{i'}\right) \\ & =\operatorname{Var}(x) \operatorname{Var}\left(\frac{\partial \operatorname{cost}}{\partial z^{d}}\right) \prod_{i'=1}^{i-1} n_{i'-1} \operatorname{Var}\left(W^{i'}\right) \cdot \prod_{i'=i+1}^{d} n_{i'}, \operatorname{Var}\left(W^{i'}\right) \end{aligned}
Var(∂wi∂Cost)=Var(hi−1)⋅Var(∂zi∂cost)=Var(x)i′=1∏i−1ni′−1Var(Wi′)⋅Var(∂zd∂Cost)i′=i+1∏dni′Var(Wi′)=Var(x)Var(∂zd∂cost)i′=1∏i−1ni′−1Var(Wi′)⋅i′=i+1∏dni′,Var(Wi′)我们考虑一种简单的网络:如果现在令所有层的大小一样并且对所有层采用相同的初始化方式,那么有:
Var
(
h
i
)
=
Var
(
x
)
[
n
Var
(
W
)
]
i
\operatorname{Var}\left(h^{i}\right)=\operatorname{Var}(x)[n \operatorname{Var}(W)]^{i}
Var(hi)=Var(x)[nVar(W)]i
∀
i
,
Var
(
∂
cos
t
∂
z
i
)
=
Var
(
∂
cos
t
∂
z
d
)
[
n
V
a
r
(
W
)
]
d
−
i
\forall i, \operatorname{Var}\left(\frac{\partial \cos t}{\partial z^{i}}\right)=\operatorname{Var}\left(\frac{\partial \cos t}{\partial z^{d}}\right)[n V a r(W)]^{d-i}
∀i,Var(∂zi∂cost)=Var(∂zd∂cost)[nVar(W)]d−i
∀
i
,
Var
(
∂
C
o
s
t
∂
w
i
)
=
Var
(
x
)
Var
(
∂
Cost
∂
z
d
)
[
n
Var
(
W
)
]
d
−
1
\forall i, \operatorname{Var}\left(\frac{\partial C o s t}{\partial w^{i}}\right)=\operatorname{Var}(x) \operatorname{Var}\left(\frac{\partial \operatorname{Cost}}{\partial z^{d}}\right)[n \operatorname{Var}(W)]^{d-1}
∀i,Var(∂wi∂Cost)=Var(x)Var(∂zd∂Cost)[nVar(W)]d−1由(15)(16)(17)可以看出激活值方差和层数相关,反向传播的梯度方差和层数是有关系的,而参数梯度的方差和层数无关。前面也提到了这可以解释图2和图3中出现的现象。
公式(16)对应原文的公式(13),原文中的公式(13)应该是有误的。
满足Glorot条件的初始化
为了满足公式(8)(9),结合公式(12)(13),我们将Glorot条件转换成:
∀
i
,
n
i
V
a
r
(
W
i
+
1
)
=
1
∀
i
,
n
i
+
1
Var
(
W
i
+
1
)
=
1
\begin{aligned} \forall i, n_{i} V a r\left(W^{i+1}\right) &=1 \\ \forall i, n_{i+1} \operatorname{Var}\left(W^{i+1}\right) &=1 \end{aligned}
∀i,niVar(Wi+1)∀i,ni+1Var(Wi+1)=1=1作者取均值来同时满足(17)(18):
∀
i
,
Var
(
W
i
+
1
)
=
2
n
i
+
n
i
+
1
\forall i, \operatorname{Var}\left(W^{i+1}\right)=\frac{2}{n_{i}+n_{i+1}}
∀i,Var(Wi+1)=ni+ni+12这个方差对应如下均匀分布:
W
∼
U
[
−
6
n
i
+
n
i
+
1
,
6
n
i
+
n
i
+
1
]
W \sim U\left[-\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}, \frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}\right]
W∼U[−ni+ni+16,ni+ni+16]简单网络:
现在假设各层的大小一样,则由公式(19)可知各层的参数方差一样
Var
(
W
)
=
1
n
\operatorname{Var}(W)=\frac{1}{n}
Var(W)=n1把(20)代入公式(15)(16)可以很容易看出,激活值的方差和层数无关,反向传播梯度的方差和层数无关。在这个简单的网络中,Xavier初始化确实保证了Glorot条件。
激活值和梯度特性实验
下面的实验都是在tanh神经网络上进行的。
初始化后的激活值和梯度特性
在标准化初始化中,我们绘制了tanh激活函数的初始激活值、初始反向传播梯度和初始参数梯度。这里同样以tanh激活函数为例,讨论Xavier初始化的这些属性图。
- 初始激活值
各层激活值的方差不变,确实满足了Glorot条件一。
- 初始反向梯度
反向梯度的方差不变,确实满足了Glorot条件二。
- 初始参数梯度
参数梯度的方差也符合我们的预期:方差不变。
但是Xavier初始化得到的参数梯度比标准初始化得到的参数梯度大了一个数量级。
训练过程中的激活值特性
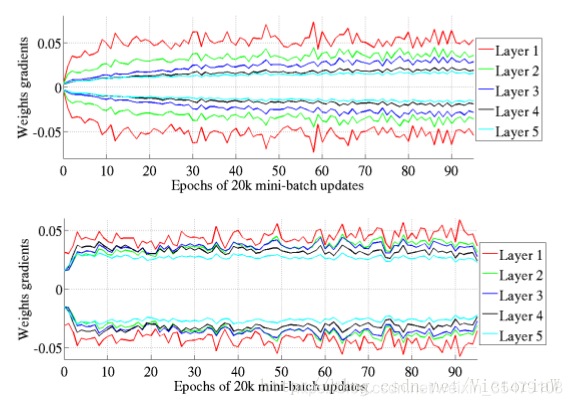
训练过程中标准初始化和Xavier初始化的参数梯度的标准偏差比较
训练过程中中标准初始化和Xavier初始化的测试误差比较
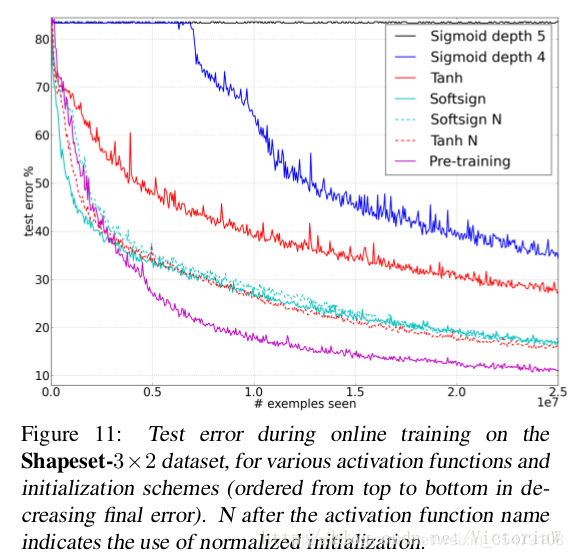
Xavier初始化的缺点
- 因为Xavier的推导过程是基于几个假设的,其中一个是激活函数是线性的。这并不适用于ReLU激活函数。另一个是激活值关于0对称,这个不适用于sigmoid函数和ReLU函数。所以可以看到图11中并没有对sogmoid网络应用Xavier初始化。
可以实验验证sigmoid激活函数用Xavier初始化后的初始化激活值、反向梯度、参数梯度特性:
我以MNIST做训练数据,发现标准初始化和Xavier初始化得到的初始激活、参数梯度特性是一样的。激活值的方差逐层递减,参数梯度的方差也逐层递减。