一、什么是时间和空间复杂度?
📚 那么在了解时间复杂度和空间复杂度之前,我们先要知道为何有这两者的概念:
首先我们要先了解"算法",在之前我们学习过关于"一维前缀和与差分","二维前缀和与差分"这部分知识,而这部分知识就属于基础算法中的"前缀和"与"差分"的两部分,也就是说它们也是算法。
而除了它们以外,其实我们在之前的学习中,大部分的知识也都和算法脱不开干系,例如:"枚举","位运算","冒泡排序","二分查找"等,只不过在当时学习时,我们主要在意的是"如何解题",并没有深究题解的时间效率和空间效率。
📕 我们先引入一个小题:
有一高度10阶的楼梯,每步只能上一阶或二阶,请问从下往上走,一共能得到多少种走法?
这题大家应该是很熟悉的,通过我们之前学习过的函数递归思想,脑海中的解题思路就会是:
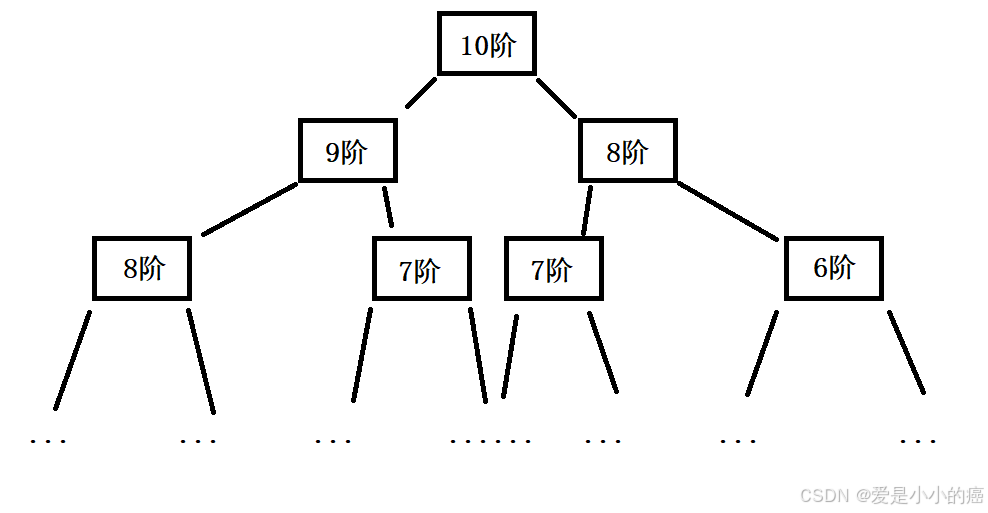
反向思考一下,如果我们距离最后一步到达10阶,就是有两种情况"8->10 或 9->10",而"8->10"就需要我们先走到8阶,相应的"9->10"就需要我们先走到9阶,所以从0阶走到10阶的走法应该等于"0阶到9阶的走法+0阶到8阶的走法"。
相应的,之前的7,8,9阶也皆是如此,于是我们便能写出递归函数:
public static void main(String[] args) {
System.out.println(climbStairs(10));
}
public static int climbStairs(int num){
if(num == 0){
return 0;
}
if(num == 1){
return 1;
}
if(num == 2){
return 2;
}
return climbStairs(num - 1) + climbStairs(num - 2);
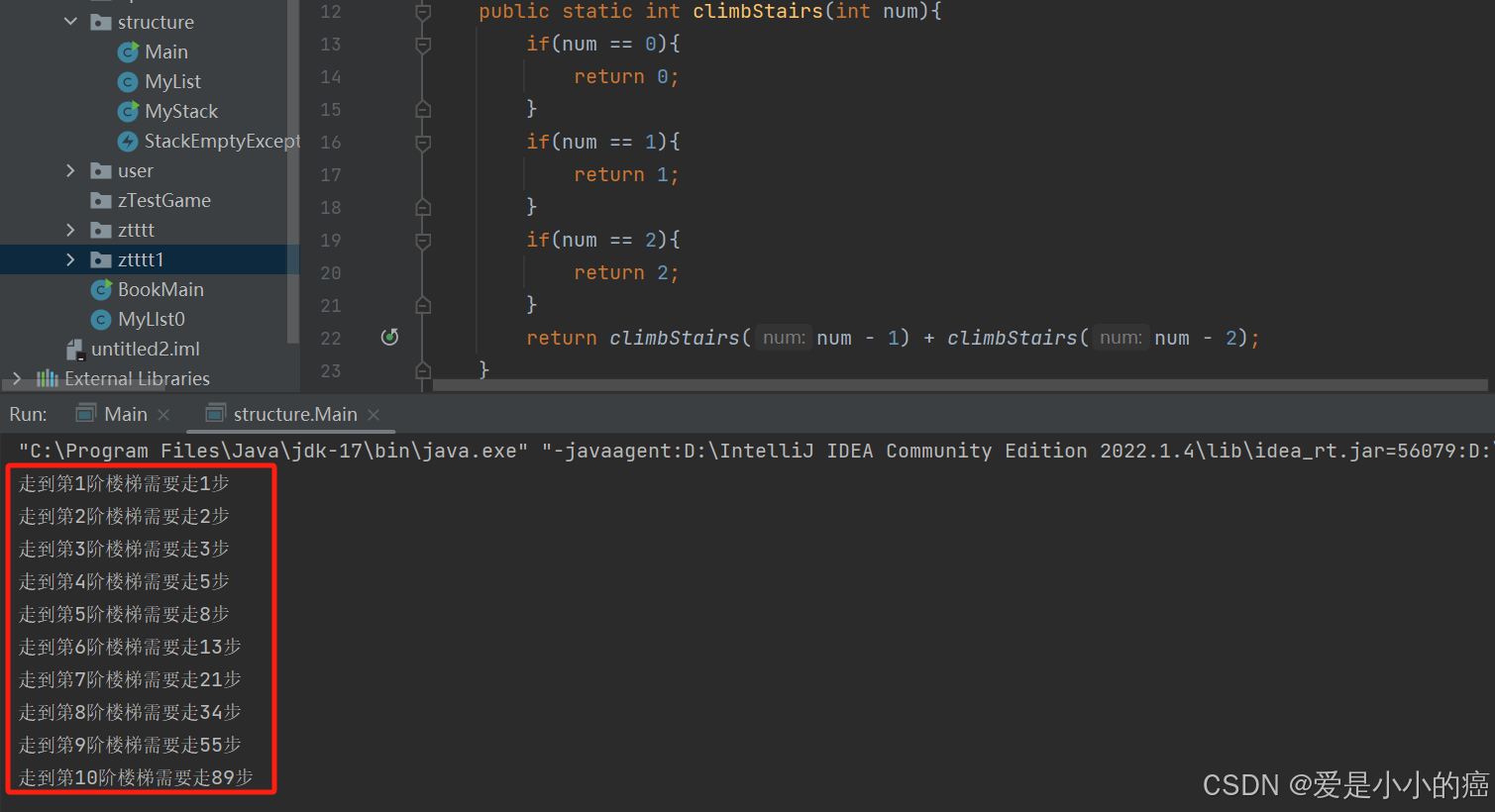
}这就是我们之前学习过的"函数递归"了,这样的方法确实能得到答案,但是让我们现在思考一下,这个方法的效率是否够高呢?按照我们这段代码的思路来看,运算过程中实际上是这样的:
随着每多1阶楼梯。我们要计算的步骤就都相应乘以2,并且大部分的数据都是重复的。如果我们输入一个较大的数,那么这种算法的时间损耗是相当大的。
所以由此看来,这个方法就不算是一个高效率的算法,而判断算法效率如何,就需要我们所提到的"时间和空间复杂度"了。
时间复杂度和空间复杂度是用来表示一个算法的优劣程度的
二、时间复杂度
① 时间复杂度的概念
📚 时间复杂度的定义:
算法的时间复杂度是一个数学函数,它能够大致的表示出一个算法的运行时间,因为一个算法运行所消耗的时间,是不能算出精确值的,只有将代码运行一遍,才能够得出对应精确的时间,但是总不能将所有的算法都测试一遍,这样太麻烦了,于是就有了时间复杂度的分析方法:算法中的基本操作执行次数,就称为算法的时间复杂度。
② 大O渐进表示法
📚 我们先举一个例子,试着求一下这段代码的时间复杂度:
public static int fun(int n){
int a = 0;
for(int i = 0;i < n;i++){
a++;
}
return a;
}这段代码我们可以看出,传入n,其中基本操作执行次数就也是n,故此代码的时间复杂度为O(n)。
📚 那么如果我们在其中掺杂了多端基本操作,使得执行次数的函数变得较为复杂呢:
public static int fun(int n){
int a = 0;
for(int i = 0;i < n;i++){
a++;
}
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
a++;
}
}
a++;
a++;
a++;
return a;
}这段代码中的基本操作执行次数就就稍微比较多了,我们分别来看:第一段的for循环的基本操作次数为n,而第二段的for循环嵌套的基本操作次数为n^2,第三段的基本操作次数3,所以得到的基本操作次数为:n + n^2 + 3;而所谓的大O渐进法就是为了简化此等函数式的。
③ 推导大O阶方法
📕 用常数1取代运行时间中的所有加法常数。
📕 在修改后的运行次数函数中,只保留最高阶项。
📕 如果最高阶项存在且不是1,则去除以这个项目相乘的常数。
由于我们并不需要计算精确的执行次数,我们就可以将式子中基本操作次数占比较少的部分省略掉,所以我们该式子的时间复杂度可以简化为O(N^2)。
(注:常数阶的时间复杂度是O(1),代表是常数次,不是1次,只要是常数,都用O(1)进行表示)
这里我们就可以引用一下刚刚我们所提出的经典问题"爬楼梯问题",来算一下刚刚我们那个不完美的方法的时间复杂度为多少~
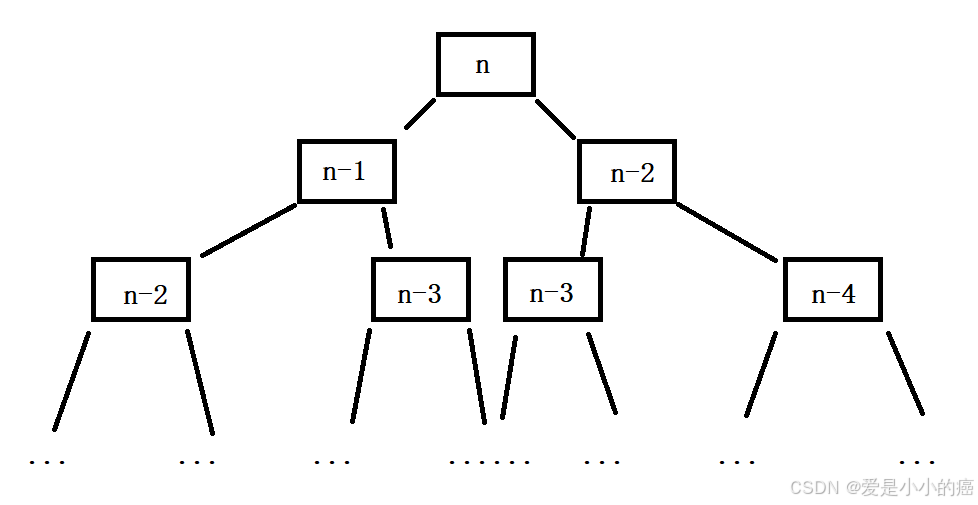
我们仍然看之前的思路图,如果要上n阶楼梯,那么就要算(n-1)阶,(n-2)阶,而得到(n-1),就要知道(n-2)阶,(n-3)阶分别的可能次数,所以可以得到此图:
这像是一棵二叉树,高度为N-1,节点个数就接近2的N-1次方,所以时间复杂度近似看成O(2^N)。
📚 另外有些算法的时间复杂度存在最好、平均和最坏情况:
📕 最坏情况:任意输入规模的最大运行次数(上界)
📕 最好情况:任意输入规模的最小运行次数(下界)
📕 常见的时间复杂度量级:
| 常数阶 | O(1) |
| 对数阶 | O(logN) |
| 线性阶 | O(n) |
| 线性对数阶 | O(nlogN) |
| 平方阶 | O(n^2) |
| 立方阶 | O(n^3) |
| K次方阶 | O(n^k) |
| 指数阶 | O(2^n) |
顺便一提,一般情况下我们的电脑的单秒运算量大概为 2e8次 我们在平时刷题时也可以按照这个与时间复杂度结合,就能大致估算运行时间了~
三、空间复杂度
空间复杂度是一个函数,它能够描述一个算法执行所需的额外存储空间,同样用大O渐进法表示,如O(1)、O(n)、O(n^2)等。空间复杂度能够直接影响算法对内存资源的使用。
在我们平时刷题,或者算法竞赛中,题目会给出空间限制,通常以MB为单位。计算空间复杂度时,我们估算程序使用的内存,基本单位换算如下:
📕 8 b = 1 B
📕 1 KB = 1024 B
📕 1 MB = 1024 KB
📕 1 GB = 1024 MB
我们要知道,int占用4字节,long占用8字节,double占用8字节等,运算空间复杂度需要我们将代码运行过程中所有字节相加并且转换为MB。
📚 接下来让我们看几段代码练习一下:
public static void main(String[] args) {
//1
int[] n = new int[10000000];
//2
long[][] n1 = new long[2000][3000];
}📕 一个大小为 n = 10^7 的int数组,内存消耗为:4e7字节,换算成MB为 4e7/(1024*1024) 约等于38.1MB。
📕 一个大小为 2000 * 3000 的 long 二维数组,内存消耗为:8 * 2000 * 3000字节,换算成MB为(8 * 2000 * 3000) / (1024*1024) 约等于45.78MB。
public static void main(String[] args) {
int[] arr = {7,9,4,8,5,6,1,2,3};
bubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
int tmp = array[i];
array[i] = array[i - 1];
array[i - 1] = tmp;
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}📕 由于bubbleSort使用的都是常数额外空间,于是空间复杂度为O(1)
public static void main(String[] args) {
System.out.println(fun(10));
}
public static int fun(int n) {
int num = 0;
int[] m = new int[n];
for(int i = 1;i <= n;i++){
num++;
}
return num;
}📕 第一行创建了int型变量,此为O(1),而后第二行创建一个数组,这个数据占用大小为n,后续的代码中并没有创建新的变量,故不用看。则使用的额外空间式子为1 + n,空间复杂度为O(n)
四、优化爬楼梯问题
📚 那么经过几道题的练习,我们再回过头来看我们最开始举例的"爬楼梯问题":
刚刚使用递归的方式求解"爬楼梯问题",我们得到的对应信息为:
时间复杂度为:O(2^n)
空间复杂度为:O(n)
我们刚刚已经意识到了,O(2^n)的时间复杂度有多么可怕,并且O(n)的空间复杂度也并不是特别优秀,那么我们应该如何对其进行优化呢?
时间复杂度太高的原因是因为我们从上而下的进行分支,而这些分支中又出现了很多的重复项,导致我们的代码会在无用的地方浪费很长时间。而想要对从上而下的分支进行操作并且判断是否重复,是并不容易的,那么我们不妨转换一下思路,我们可以从底向上的,一步一步通过迭代的方式来尝试一下:
首先我们先算出从1阶到10阶需要走的步数:
我们将其写入表格中:
然后让我们一步一步的观察其中的规律:
1阶2阶与3阶的关系:
2阶3阶与4阶的关系:
3阶4阶与5阶的关系:
我们可以观察到一个现象,在每一次的迭代中,F(N)只与F(N - 1)和F(N - 2)有关,也就是说当我们想求一个状态时,只需要保留之前的两个状态就足够了,之前的数据就可以扔掉不要了。
这就是最最简单的一个动态规划问题~
public static int climbStairs(int num){
if(num == 0){
return 0;
}
if(num == 1){
return 1;
}
if(num == 2){
return 2;
}
int a = 1;
int b = 2;
int temp = 0;
for(int i = 3;i <= num;i++){
temp = a + b;
a = b;
b = temp;
}
return temp;
}一共只用了一次for循环,这段代码的时间复杂度显而易见是O(n),而我们只使用了两或三个变量,则空间复杂度为O(1)~
趁热打铁,既然已经讲了这题了,有兴趣的小伙伴也可以写一下这题~就是一样的道理,只是多了一个(一步迈三阶)的可能~实际上我们只需要多写出一个(n == 3)的情况,以及使temp变成(a + b + c)就可以了~
面试题 08.01. 三步问题 - 力扣(LeetCode)
class Solution {
public int waysToStep(int n) {
if(n < 1){
return 0;
}
//一阶台阶1种走法
if(n == 1){
return 1;
}
//两阶台阶2种走法
if(n == 2){
return 2;
}
//三阶台阶4种走法
if(n == 3){
return 4;
}
long a = 1;
long b = 2;
long c = 4;
long temp = 0;
//F(n) = F(n - 1) + F(n - 2) + F(n - 3);
//同理,后续的迭代中F(n)也只与F(n - 1) , F(n - 2) , F(n - 3)相关:
for(int i = 4;i <= n;i++){
temp = a + b + c;
a = b;
b = c;
c = temp;
a = a % 1000000007;
b = b % 1000000007;
c = c % 1000000007;
temp = temp % 1000000007;
}
return (int)temp;
}
}那么这次关于时间和空间复杂度的知识就为大家分享到这里啦,作者能力有限,如果有什么讲的不够清楚或者有错的地方还请多多在评论区指出,我们下次再见咯~