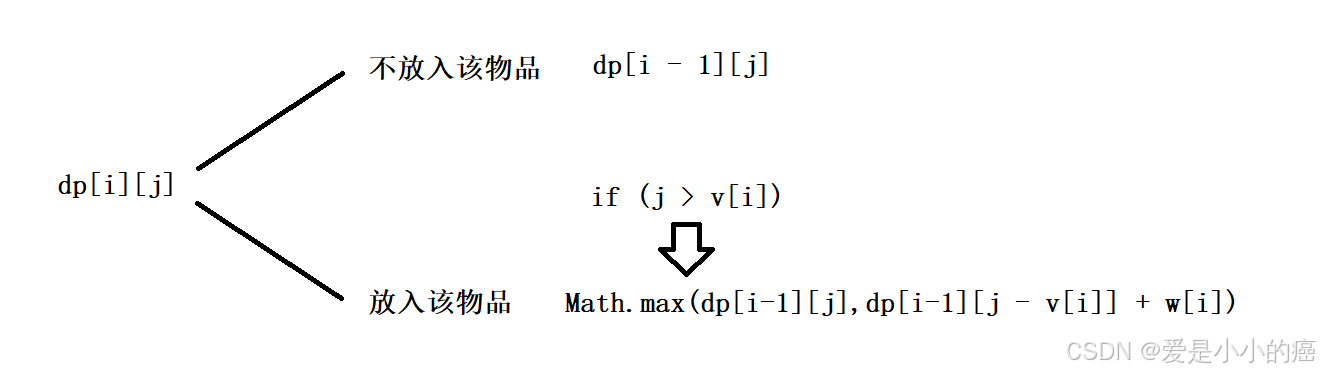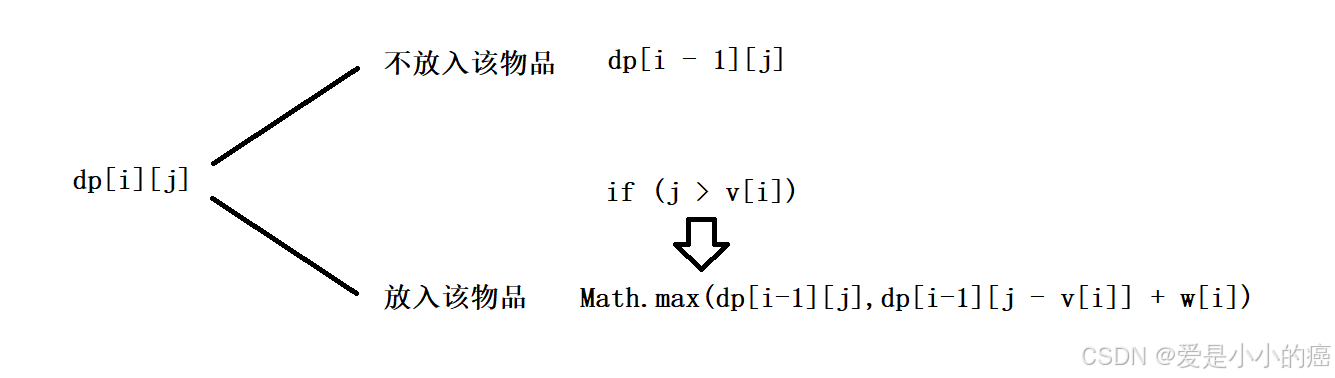一、什么是背包问题?
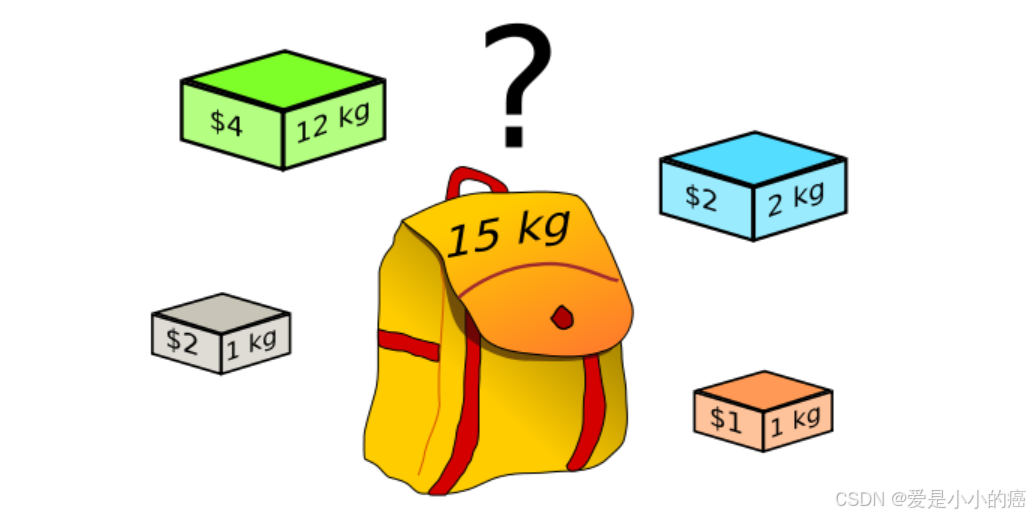
背包问题,就像是你准备去旅行,但只有一个容量有限的背包。
你面前摆满了各种物品,每件都有自己的重量和价值。你的目标是挑选一些物品放进背包,使得总重量不超过背包的容量,同时总价值尽可能大。
想象一下,你站在一堆宝物前,有闪闪发光的宝石、厚重的书籍、小巧的工具等。你需要决定带哪些宝物上路,既要确保背包不会太重,又要让这些宝物的总价值最高。
而背包问题又具有非常多的种类,也正因为如此,背包问题在动态规划中也是个比较难的问题。
📕 01 背包问题:每个物品只有一个
📕 完全背包问题:每个物品有无限多个
📕 多重背包问题:每件物品最多有 ? 个
📕 混合背包问题:每个物品会有结合上面三种情况...
📕 分组背包问题:物品有 n 组,每组物品里有若干个,每组里最多选一个物品。
而以上的背包问题中,又会根据"背包是否装满"的情况再细分为两类:
📖 一定装满背包的情况下,求最大价值为多少
📖 不一定装满背包的情况下,求最大价值为多少
所以说,如果就所有情况而言,背包问题确实是一种非常繁琐且复杂的问题~所以不管在比赛还是面试中,背包问题的重要程度都非常高~
不过话又说回来了,如果不去打特别高级的比赛,只是应对面试的话,学习 "01背包" 和 "完全背包" 就已经足够应对了 (leetcode上连多重背包的题都没有)。
所以本篇文章,我们将由浅入深的详细讲解 "01背包" ~
二、01背包
① 暴力思路
在讲解动态规划解题思路之前,我们先引入一个暴力解题的思路:
我们可以先不考虑背包的容量状态,先对物品进行分组:
假如此时我们拥有 3 件物品,'0' 代表对应物品没有放入背包,'1' 代表对应物品放入背包。
那么我们就能够通过 dfs 来求出所有物品分别为 '0','1' 状态的分组:
最后再将所有的情况一一检查,并求出不超过背包体积的情况下,价值最大的情况即可。
那么这种思路虽然容易理解,但他的时间复杂度为O(2^n),这是一个指数级别的复杂度,是非常可怕的。所以我们这里就摒弃掉这里的想法了。
② 二维dp解题
第一问(不一定装满)
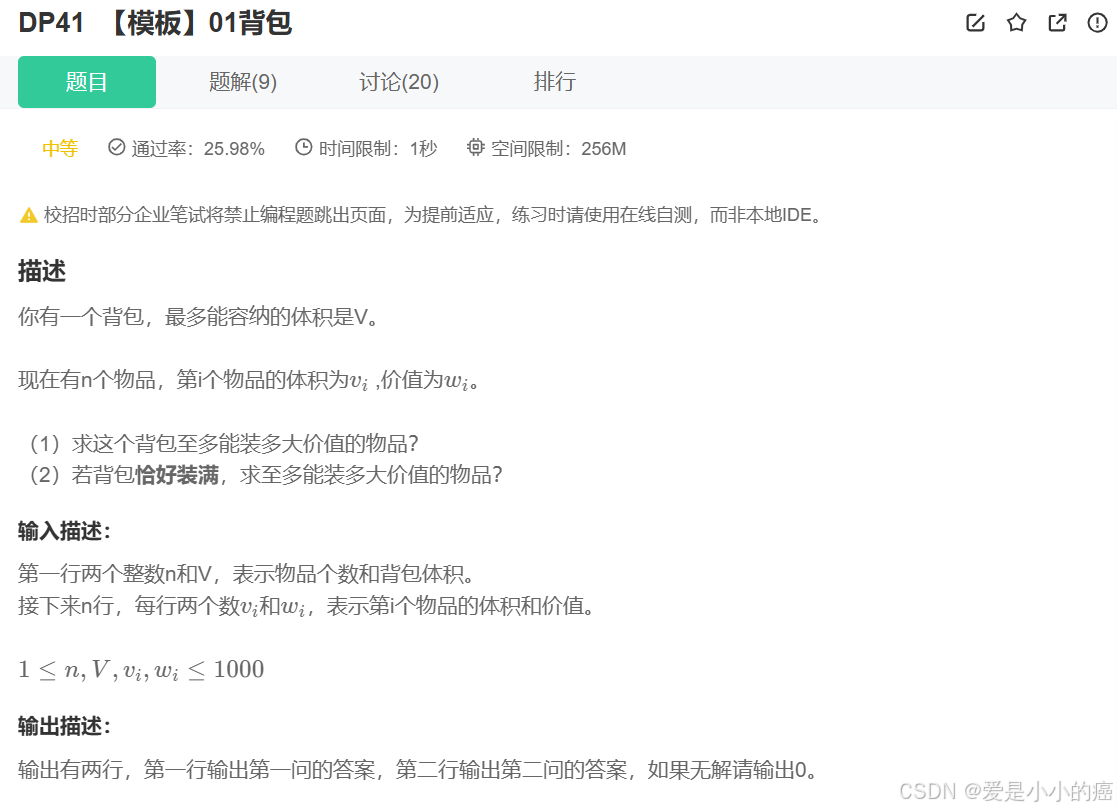
我们来看一眼测试用例:
其中 3 代表物品的数量,5 代表背包的容量,剩余每行都是物品的属性,分别为(体积)和(价值)
那么我们可以用一个表格来将这些物品具体的归纳一下:
| 编号 | 体积 | 价值 |
| 1 | 2 | 10 |
| 2 | 4 | 5 |
| 3 | 1 | 4 |
那么当不要求一定装满背包时,我们可以选取 1号 和 3号 装入背包,总价值为 14。
而要求背包一定装满时,我们只能选择 2号 和 3号 装入背包,此时的总价值为 9。
1. 状态转移方程
📚 接下来我们分析它的状态表示:
和分析其他动态规划问题是一样的,通过问题得知这是一个将物品放入背包并求价值的问题。
我们先尝试用最常规的思路来思考,此时我们的 dp 表应该是一个一维数组 dp[ i ]
此时 dp 表的含义是:在访问到第 i 个物品时,背包中能存放的最大价值。
我们用 v[ i ] 表示体积,w[ i ] 表示价值。
那么我们就要注意,每当我们访问到一个物品时,分别会发生几种情况?而发生这种情况的前提下,我们又要注意哪些其他因素?同时在这种状态转移的过程中,又该如何对应的解决?
📚 分析会发生几种情况:
最直观的来看,我们能知道,遍历到一个物品时,存在 "放入背包" 和 "不放入背包" 这两种情况。
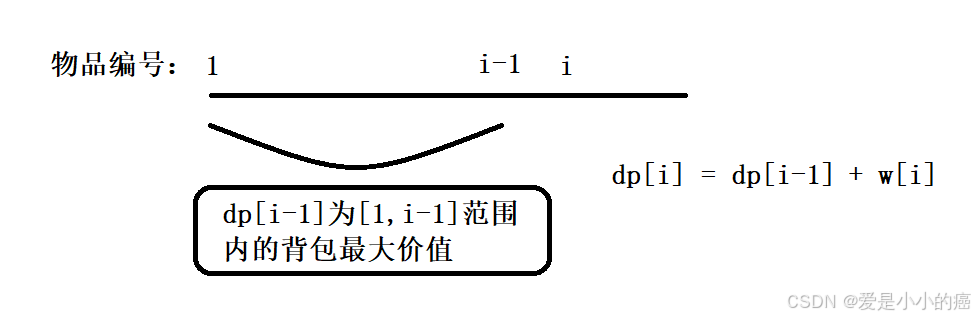
📕 当 "不放入背包" 的情况下,很容易理解,我们只需要保持dp表中上一个位置的最大值即可,毕竟我们没有放入背包就代表此时什么都不进行改变。
📕 当 "放入背包" 的情况下,需要考虑的就比较多了,我们需要放入新的物品,那么 dp[ i ] 所存储的价值应该是 dp[ i - 1 ] 的价值再加上此时物品的价值。
📚 分析应该注意哪些因素:
📕 当 "不放入背包" 的情况下,我们暂且还看不出什么问题。
📕 当 "放入背包" 的情况下,我们就要注意,想要放入新的物品,得先知道当前背包的容量是否足以放下当前物品,那么就出现问题了:
我们此时假设的 dp 表为一维dp表,而用这个状态表示的 dp 表是无法得知背包的容量,以及无法确定背包此时是否能够放入新物品的。
所以我们就需要改换思路,创建一个 二维dp表 dp[ i ][ j ]
新 dp 表代表的含义是:遍历到第 i 个物品时,背包容量为 j 的情况下,能够获得的最大价值
那么通过这个新的 dp 表,我们就能够顺利的进行接下来的工作了。
📚 分析如何解决对应情况:
📕 当 "不放入背包" 的情况下,不需要改变,仍然是取上个状态的值即可。
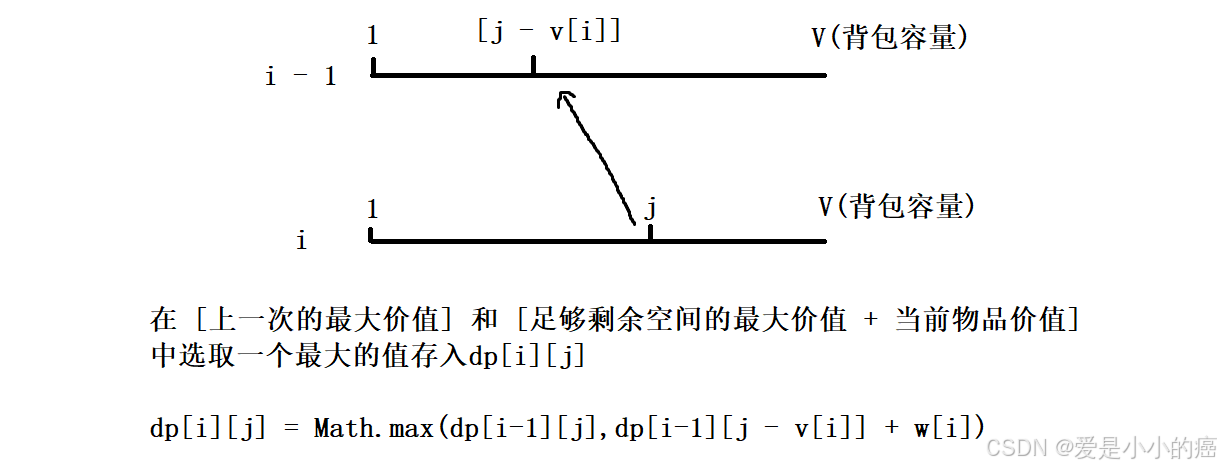
📕 当 "放入背包" 的情况下,我们就需要考虑,当前的背包容量 j 是否足够我们进行 "放入" 的操作( j > v[ i ] ),如果足够,我们还需要像上述情况一样,在之前的状态中找一个最大价值的情况。
这个 "找最大价值" 也是有前提的,我们找到的这个最大值情况下,背包可能已经装了物品,那么我们还需要确保 "选取的最大值,背包中的剩余空间足够放下当前物品"
这种情况也就是 ( j - v[i] >= 0 ),而在合法范围内,dp[i - 1][j - v[i]]代表的就是最大值,所以直接选取 dp[i - 1][j - v[i]] 即可。
那么解决完所有问题后,我们的状态转移方程也就出来了:
2. 初始化
初始化的目的是防止在填表过程中出现越界访问的情况~
所以如何初始化,是要根据我们推理出的状态转移方程来决定的。我们上面得到的状态转移方程中用到了 [ i - 1 ] 和 [ j - v[ i ] ],这就代表在填表过程中,我们会访问到 [当前的上一列] 和 [当前的左侧] 区域。
所以为了防止越界,正常来说我们是需要将 [最左侧的一列] 和 [最上的一行] 都先初始化的,但这样的初始化难度很高,其中的运算也会大大提升时间的消耗。
所以我们可以开辟一个比实际需要更大的一个数组,这种方法在平常的动态规划题中也会经常应用到,也是屡试不爽的~
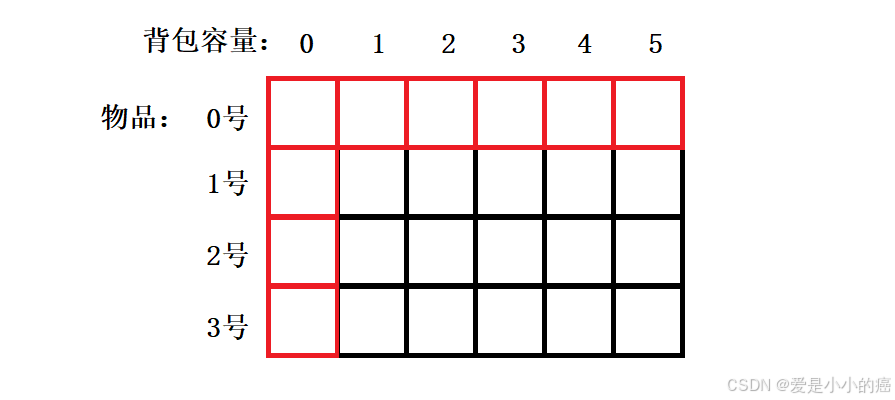
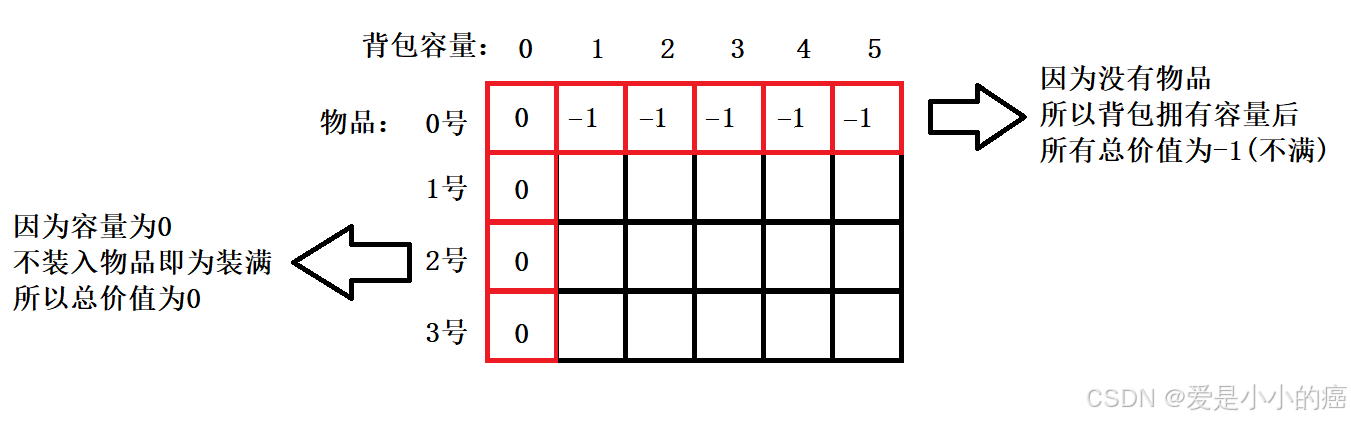
开辟好后大概就像这样:
📕 第一行中,代表 [没有遍历到物品] 所以价值无论如何都是 0 ~
📕 第一列中,代表 [背包永远没有容量] 所以价值也全都是 0 ~
这样就超级简单的解决了初始化问题...(根本没有初始化啊喂...)
3. 填表顺序
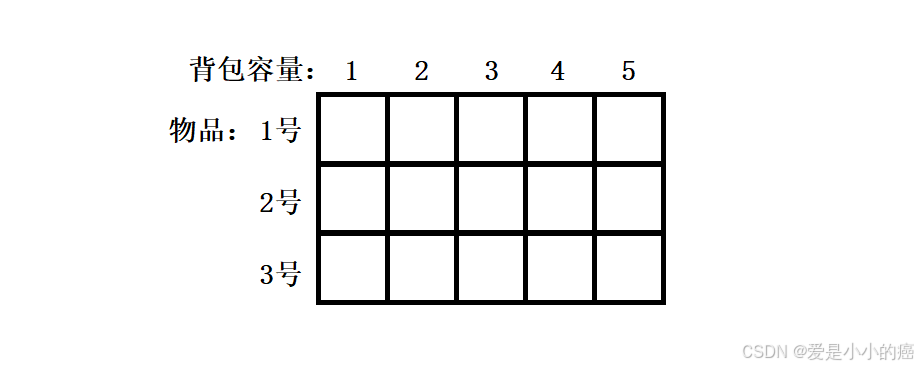
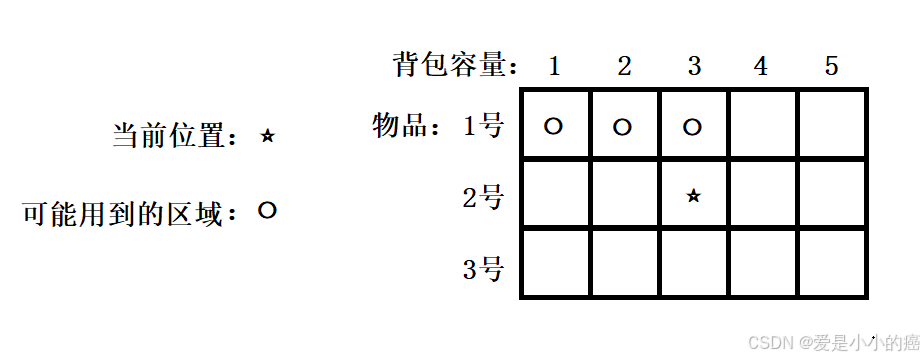
由于红色的区域是我们额外开辟出来,便于初始化的那部分空间~所以后续我们实际进行操作的时候,可以直接把图看作这样:
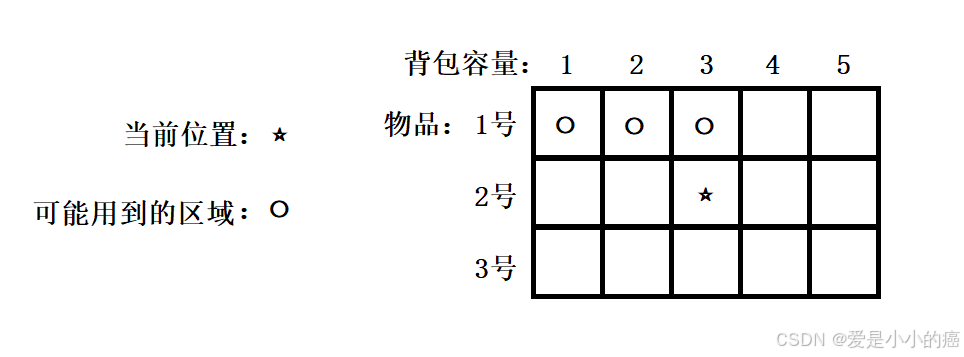
而我们填表需要用到的值,大概可以确认为这两个方向:
所以我们的填表顺序只需要保证 [从上往下] 即可
代码示例
public class Main {
public static int N = 1005;
//----------二维解法----------
public static void main(String[] args)
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int V = in.nextInt();
// v->体积 w->价值
int[] v = new int[N];
int[] w = new int[N];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
// 1. 创建dp表
// 代表选择第 i 个物品时,背包最大有 j 个空间情况下,能存放的最大价值
int[][] dp = new int[N][N];
// 2. 初始化(第一问)
// 3. 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
// 不装入该物品(仍保持上次的最高值)
dp[i][j] = dp[i - 1][j];
// 装入该物品
if (j >= v[i]) {
// 比如背包的空间有10,如果此时的物品体积为3
// 那么说明剩余体积小于3时,无法存放该物品 -> (j >= v[i])
// 当我们想把体积为3的物品放入5的位置时,
// 按理来说我们要在[1,4]的范围内找到一个最大值,再加上w[i]
// 但这个最大值不是随便找的,这个最大值的前提是[要给当前物品留有充足空间]
// 而这个充足空间就代表 [j - v[i]]
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
// 4. 返回值
System.out.println(dp[n][V]);
}第二问(一定装满)
对于第二问来说,我们只需要修改一些小细节即可
1. 状态转移方程
让我们再来回顾一下第一问的 dp 表的含义:
dp 表代表的含义是:遍历到第 i 个物品时,背包容量为 j 的情况下,能够获得的最大价值
从这里可以看出,并没有对背包的容量进行限定,那么此时背包是否装满,我们是不知道的
所以在这里我们需要对 dp 表的含义进行一下修改:
新 dp表的含义:遍历到第 i 个物品时,背包容量为 j 并装满情况下,能够获得的最大价值
再来看一下我们第一问的状态转移方程:
这个状态转移方程中,dp[ i ][ j ]得到的数据,是存在 [背包不满] 的情况的,而想要使这个动态转移方程符合我们 新dp表 的含义,就需要另外创建一种状态定义:
dp[ i ][ j ] = -1 时,代表此时背包不满,也就是此种状态不存在。
📕 当 "不放入背包" 的情况下,可以不用修改,因为 dp[i - 1][j] 代表的含义就是 [遍历到第 i - 1 个物品时,背包内总体积为 j 的最大值],同时当 dp[i - 1][j] 为-1时,也符合dp[i][j]的值。
📕 当 "放入背包" 的情况下,我们需要用到 dp[i - 1][j - v[i]] ,而对于这个值我们就不能直接进行操作了。
因为就算 dp[i - 1][j - v[i]] 为 -1,加上 w[i] 后也仍有可能超过 dp[i - 1][j],而当它超过 dp[i - 1][j] 时,就会将 dp[i][j] 的值改变成这个错误的 不存在的值
所以综上所述,我们只需要对原来的状态转移方程做一个约束即可:
2. 初始化
这里的初始化也是一个需要修改的点:
📕 第一行中,代表 [没有遍历到物品] 所以背包永远不满,都为 -1 ~
📕 第一列中,代表 [背包永远没有容量] 所以永远算满,价值也全都是 0 ~
3. 填表顺序
和上面一样,这里没有区别~
代码示例(完整)
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static int N = 1005;
//----------二维解法----------
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int V = in.nextInt();
// v->体积 w->价值
int[] v = new int[N];
int[] w = new int[N];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
// 1. 创建dp表
// 代表选择第 i 个物品时,背包最大有 j 个空间情况下,能存放的最大价值
int[][] dp = new int[N][N];
// 2. 初始化(第一问)
// 3. 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
// 不装入该物品(仍保持上次的最高值)
dp[i][j] = dp[i - 1][j];
// 装入该物品
if (j >= v[i]) {
// 比如背包的空间有10,如果此时的物品体积为3
// 那么说明剩余体积小于3时,无法存放该物品 -> (j >= v[i])
// 当我们想把体积为3的物品放入5的位置时,
// 按理来说我们要在[1,4]的范围内找到一个最大值,再加上w[i]
// 但这个最大值不是随便找的,这个最大值的前提是[要给当前物品留有充足空间]
// 而这个充足空间就代表 [j - v[i]]
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
// 4. 返回值
System.out.println(dp[n][V]);
// 2. 初始化(第二问)
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= V; j++) {
dp[i][j] = 0;
}
}
// 以-1代表 选择到第 i 个物品时,不存在正好装满 j 个空间的情况.
for (int i = 1; i <= V; i++) {
dp[0][i] = -1;
}
// 3. 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
// 不装入该物品(仍保持上次最高值)
dp[i][j] = dp[i - 1][j];
// 当包内剩余空间足够时,我们必须判断放入当前物品后
// 是否能够使背包达到装满的情况,比如:
// 如果背包空间为10,当前物品体积为3,按照(第一问)的逻辑
// 我们能对[0,7]的位置进行检查判断,但是直接装入,有可能发生
// (对4位置装入,代表[4~6]存在物品,而[0~3]可能仍然为空
// 所以我们必须确保,在4位置装入之前,3位置装满的情况存在)
// 也就是 dp[i - 1][j - v[i]] >= 0;
if (j >= v[i] && dp[i - 1][j - v[i]] >= 0) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
System.out.println(dp[n][V] > 0 ? dp[n][V] : 0);
}
}③ 一维dp解题(优化)
看到这里,大家可能会想,上面不是已经说过了一维dp是没办法解题的嘛?实则不然,我们上面只是说当时的 "一维dp状态表示" 没办法进行解题,而在这里我们就会讲解一下 "正确的状态表示"~
但也不是说上面的步骤就多余,我们这个 "一维dp状态表示" 的分析还是需要通过上述二维的解题方法的基础上来进行优化的,所以以上的分析也都是必然的 一定要看明白
第一问(不一定装满)
1. 状态转移方程
想要对二维dp成一维dp,实际上就是优化了空间的消耗,而想要做到此步,我们必须先知道上面的方法里,能够从哪里开始节省空间:
从上图我们可以知道以下信息:
📕 当填表时,我们需要用到上一行的数据,那么就需要保证上一行的数据不能被节省
📕 当填完一个格子后,后续遍历其他格子时,这个格子内的数据也不会再改变,代表了 01 背包问题具有(无后效性)
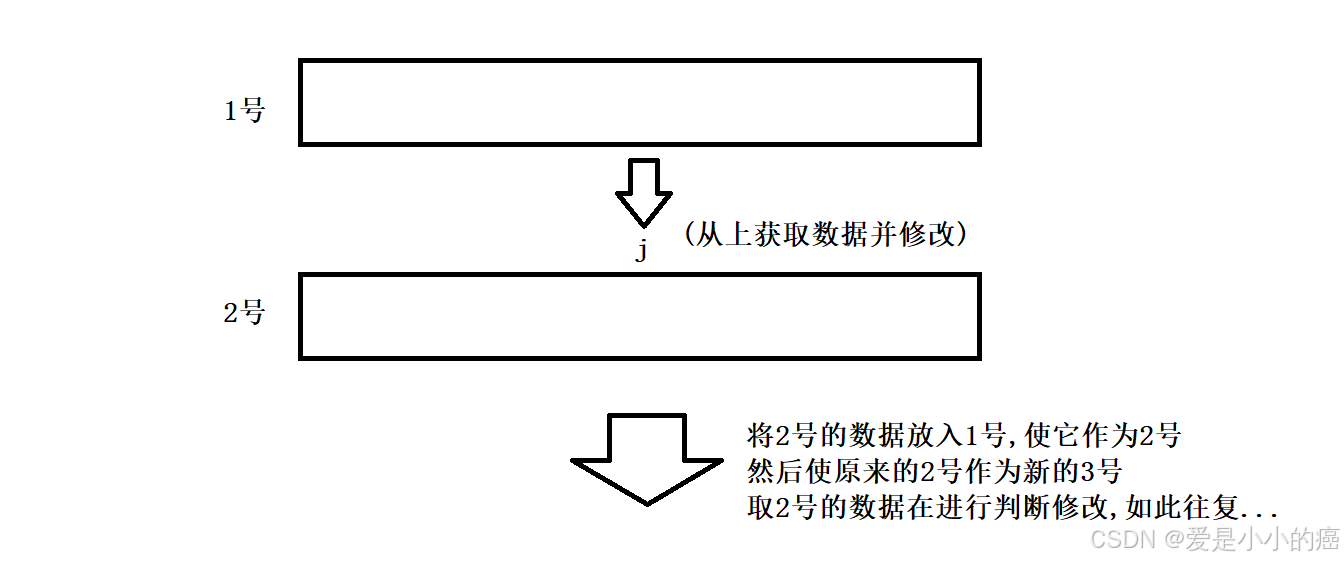
那么我们也就代表,当我们遍历到再后面的物品,如6号,7号时,那么上面的 1~5号 数据就不会再使用了,那么此时我们就可以省去这些时间,只用两个一维数组进行滚动的存储~
这样的思路已经很好了,但并不是最终优化,我们还能够再进行优化:只用一个 一维dp数组
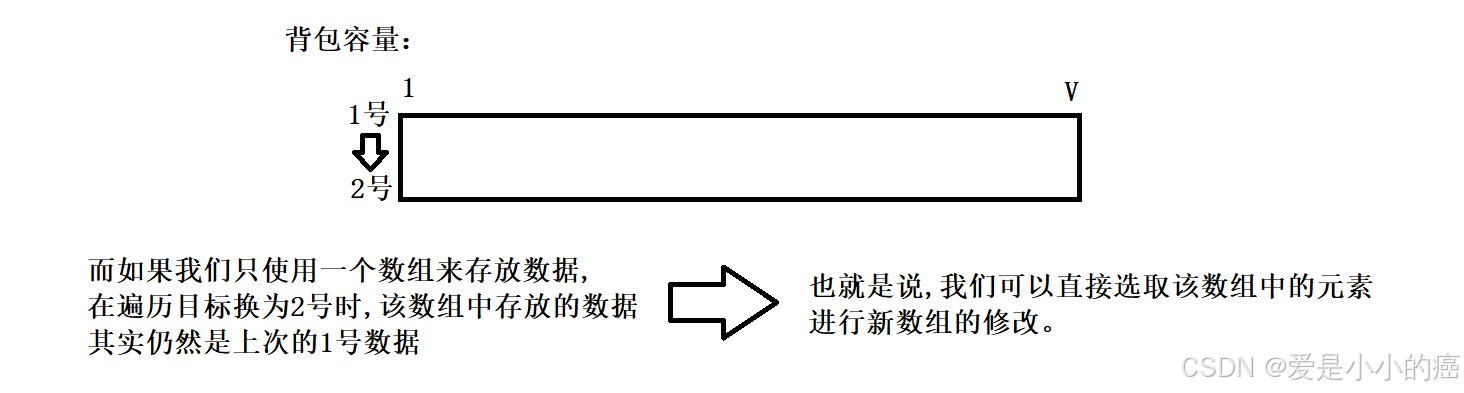
那么只选取一个数组的情况下,我们就必须保证,在修改一个背包格的时候,需要用到的数据必须没有被覆盖,必须还是原来上一行背包格的数据:
所以,这里我们就能够确认出来状态转移方程了。
和上面的还是一样的,只是需要我们把遍历顺序换一下就好了
2. 初始化
和二维dp解题的第一问思路相同~不需要改动
3. 填表顺序
在上面提到过了,必须是"从右向左"的!必须!!
代码示例
//----------一维解法----------
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int V = in.nextInt();
int[] v = new int[N];
int[] w = new int[N];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
// 1. 创建dp表
// 代表背包空间为 j 时,能够存储的最大价值
int[] dp = new int[N];
// 2. 初始化(第一问)
// 3. 填表
// 在二维数组解题时,我们需要用到[上一列同一位置]和[上一列左侧位置]
// 而使用一维数组解题时,当前数组存储的就是[上一列的数据]
// 从左往右的顺序会导致,[检查时使用左侧数据,可能已经被顶替],故改变遍历顺序
for (int i = 1; i <= n; i++) {
for (int j = V; j >= 1; j--) {
//不装入该物品(仍保持上次最高值)
//从右往左重新遍历时,[j]左侧元素都代表上次的值
//所以未修改时,dp[j]就代表上次的最高值 -> dp[j] = dp[j]
//装入该物品,与二维解法思路相同
if (j >= v[i]) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
}
// 4. 返回值
System.out.println(dp[V]);第二问(一定装满)
这里就没什么需要多说的了,步骤和思路都是一样的,注意从右往左填表即可。
代码示例
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static int N = 1005;
//----------二维解法----------
public static void main0() {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int V = in.nextInt();
// v->体积 w->价值
int[] v = new int[N];
int[] w = new int[N];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
// 1. 创建dp表
// 代表选择第 i 个物品时,背包最大有 j 个空间情况下,能存放的最大价值
int[][] dp = new int[N][N];
// 2. 初始化(第一问)
// 3. 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
// 不装入该物品(仍保持上次的最高值)
dp[i][j] = dp[i - 1][j];
// 装入该物品
if (j >= v[i]) {
// 比如背包的空间有10,如果此时的物品体积为3
// 那么说明剩余体积小于3时,无法存放该物品 -> (j >= v[i])
// 当我们想把体积为3的物品放入5的位置时,
// 按理来说我们要在[1,4]的范围内找到一个最大值,再加上w[i]
// 但这个最大值不是随便找的,这个最大值的前提是[要给当前物品留有充足空间]
// 而这个充足空间就代表 [j - v[i]]
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
// 4. 返回值
System.out.println(dp[n][V]);
// 2. 初始化(第二问)
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= V; j++) {
dp[i][j] = 0;
}
}
// 以-1代表 选择到第 i 个物品时,不存在正好装满 j 个空间的情况.
for (int i = 1; i <= V; i++) {
dp[0][i] = -1;
}
// 3. 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
// 不装入该物品(仍保持上次最高值)
dp[i][j] = dp[i - 1][j];
// 当包内剩余空间足够时,我们必须判断放入当前物品后
// 是否能够使背包达到装满的情况,比如:
// 如果背包空间为10,当前物品体积为3,按照(第一问)的逻辑
// 我们能对[0,7]的位置进行检查判断,但是直接装入,有可能发生
// (对4位置装入,代表[4~6]存在物品,而[0~3]可能仍然为空
// 所以我们必须确保,在4位置装入之前,3位置装满的情况存在)
// 也就是 dp[i - 1][j - v[i]] >= 0;
if (j >= v[i] && dp[i - 1][j - v[i]] >= 0) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
System.out.println(dp[n][V] > 0 ? dp[n][V] : 0);
}
//----------一维解法----------
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int V = in.nextInt();
int[] v = new int[N];
int[] w = new int[N];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
// 1. 创建dp表
// 代表背包空间为 j 时,能够存储的最大价值
int[] dp = new int[N];
// 2. 初始化(第一问)
// 3. 填表
// 在二维数组解题时,我们需要用到[上一列同一位置]和[上一列左侧位置]
// 而使用一维数组解题时,当前数组存储的就是[上一列的数据]
// 从左往右的顺序会导致,[检查时使用左侧数据,可能已经被顶替],故改变遍历顺序
for (int i = 1; i <= n; i++) {
for (int j = V; j >= 1; j--) {
//不装入该物品(仍保持上次最高值)
//从右往左重新遍历时,[j]左侧元素都代表上次的值
//所以未修改时,dp[j]就代表上次的最高值 -> dp[j] = dp[j]
//装入该物品,与二维解法思路相同
if (j >= v[i]) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
}
// 4. 返回值
System.out.println(dp[V]);
// 2. 初始化(第二问)
for (int j = 0; j <= V; j++) {
dp[j] = -1;
}
dp[0] = 0;
// 3. 填表
for (int i = 1; i <= n; i++) {
for (int j = V; j >= 1; j--) {
//不装入该物品(仍保持上次最高值) -> 同上
//装入该物品,与二维解法思路相同
if (j >= v[i] && dp[j - v[i]] >= 0) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
}
// 4. 返回值
System.out.println(dp[V] >= 0 ? dp[V] : 0);
}
}那么这篇关于"01背包问题"的文章到这里就结束啦,作者能力有限,如果有哪里说的不够清楚或者不够准确,还请各位在评论区多多指出,我也会虚心学习的,我们下次再见啦