Bootstrap

C语言实现 二叉排序树 的插入、删除、查找（详细图解）

1 二叉排序树定义：

如果它的左子树不为空，那么左子树上所有节点的值均小于它的根节点的值

如果它的右子树不为空，那么右子树上所有节点的值均大于它的根节点的值

根节点的左子树和右子树均是二叉排序树

（二叉排序树可能退化为链表，所以有平衡二叉树的概念；二叉排序树的中序遍历是从小到大有序的）

2 二叉排序树结构体及节点创建函数

typedef struct Tree //二叉树
{
    int data;           //数据域
    struct Tree *left;  //左子节点指针
    struct Tree *right; //右子节点指针
} Tree;
Tree *createBinarySortTreeNode(int data)
{
    Tree *node = (Tree *)malloc(sizeof(Tree));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

3 二叉排序树的节点插入

思路：将要插入节点的data与根节点data比较，如果小于根节点data，则插入根节点的左子树；如果大于根节点的data，则插入根节点的右子树；

插入子树相当于插入一个更小的树，因此可以用递归方法实现，直到找到没有子树的节点，将新节点插到其下面，成为叶子节点。

void insertBinarySortTreeNode(Tree *dataNode, Tree **root) //二叉排序树插入节点，因为根节点可能改变，所以传二级指针
{
    if (*root == NULL || dataNode == NULL)
    {
        *root = dataNode;
        return;
    }
    if (dataNode->data > (*root)->data)//如果插入节点大于原节点的data，插入节点需要放在root的右子树
    {
        if ((*root)->right == NULL)//找到插入位置
        {
            (*root)->right = dataNode;
            return;
        }
        if ((*root)->right)
            insertBinarySortTreeNode(dataNode, &(*root)->right);//递归找dataNode的插入位置
    }
    if (dataNode->data <= (*root)->data)//如果去掉等于号，表示不插入相同data的节点
    {
        if ((*root)->left == NULL)//找到插入位置
        {
            (*root)->left = dataNode;
            return;
        }
        if ((*root)->left)
            insertBinarySortTreeNode(dataNode, &(*root)->left); //递归找dataNode的插入位置
    }
}

4 二叉排序树最大键值节点获取

  • 思路：二叉排序树由于右子树节点键值均大于根节点键值，因此需要从右子树的根节点再开始查找.......直至找到最后一个右子树的右子节点，即为最大键值对应的节点。可用递归实现该过程。
Tree *maxValueOfBinaryTree(Tree *root)
{
    if (root == NULL)//空指针判断
        return NULL;
    Tree *pointer = root;
    while (pointer->right)//跳出循环后，pointer指向最后一个右子节点
        pointer = pointer->right;
    return pointer;
}

5 二叉排序树最小键值节点获取(思路同上，不再赘述)

Tree *minValueOfBinaryTree(Tree *root)
{
    if (root == NULL)
        return NULL;
    Tree *pointer = root;
    while (pointer->left)
        pointer = pointer->left;
    return pointer;
}

6 二叉排序树查找指定节点的父节点

Tree *parentNodeOfBinaryTreeNode(Tree *dataNode, Tree *root) //获取dataNode节点的父节点
{
    if (dataNode == NULL || root == NULL || root == dataNode) //空指针判断，以及root自身无父节点
        return NULL;
    Tree *pointer = root;
    Tree *parentNode = pointer;
    while (pointer != NULL && pointer->data != dataNode->data)
    {
        parentNode = pointer;
        if (dataNode->data > pointer->data)
            pointer = pointer->right;
        else
            pointer = pointer->left;
    } //每一次循环后parentNode总是pointer的父节点
    //循环跳出后，要么找到了dataNode，要么pointer为NULL了
    if (pointer == NULL)
    {
        printf("节点dataNode不存在\n");
        return NULL;
    }
    return parentNode;
}

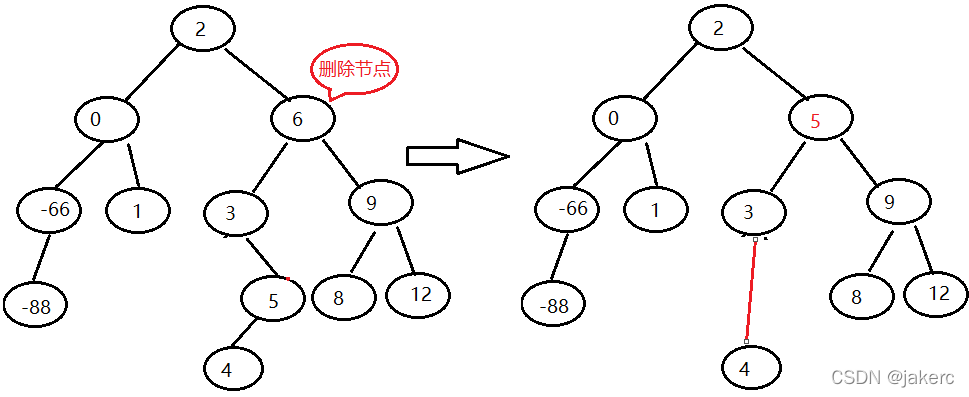
7 二叉排序树删除节点

  • 7.1 如果删除的节点是叶子节点（没有子结点），把删除节点置为NULL即可(删除节点的父节点指向NULL)；特例：如果删除节点是root节点，则root置为NULL即可
  • 7.2 如果删除的节点有一个子结点，把删除节点的父节点指向删除节点的子结点即可。特例：如果删除节点是root节点，即可认为删除链表的头节点，把第二个节点当作表头即可。
  • 7.3 如果删除的节点有两个子结点，为保证二叉排序树的有序性，需要找到与删除节点键值最接近的两个节点，由二叉树的特性知，这两个节点位于删除节点左子树的最右节点，右子树的最左节点。然后将删除节点的父节点指向其中任意一个（例如左子树最右节点，简称替代节点），替代节点的右指针指向删除节点的右子树；替代节点的父节点如果不是删除节点时，替代节点的左指针指向删除节点的左子树，替代节点的父节点指向替代节点的左子树（替代节点处于最右时没有左子树）； 特例1：删除的节点为root时 特例2：替代节点的父节点是删除节点时，可见代码分析
  • 最后释放删除节点的空间即可

 代码如下

void deleteBinarySortTreeNode(Tree *deleteNode, Tree **root) //删除二叉树中的某一个节点
{
    Tree *parentOfDeleteNode = parentNodeOfBinaryTreeNode(deleteNode, *root); //删除节点的父节点
    if (deleteNode == NULL || root == NULL)                                   //空指针判断
        return;
    if (deleteNode != *root && parentOfDeleteNode == NULL) //删除节点不是root，parentOfDeleteNode==NULL说明没有找到deleteNode或者树的root节点为NULL,直接结束;
        return;
    if (deleteNode->left == NULL && deleteNode->right == NULL) // case：1 删除节点为叶子节点的情况
    {
        if (*root == deleteNode) //删除的节点是root节点
        {
            *root = NULL;
            return;
        }
        if (parentOfDeleteNode->left == deleteNode)
            parentOfDeleteNode->left = NULL;
        if (parentOfDeleteNode->right == deleteNode)
            parentOfDeleteNode->right = NULL;
    }
    else if (deleteNode->left == NULL || deleteNode->right == NULL) // case：2 删除节点只有左子树或右子树，其中之一
    {
        if (*root == deleteNode)
        {
            if ((*root)->left != NULL) //删除节点为root节点，且root节点只有左子树
                (*root) = (*root)->left;
            else if ((*root)->right != NULL)
                (*root) = (*root)->right; //删除节点为root节点，且root节点只有右子树
        }
        else if (deleteNode->left != NULL) //删除节点只有左子树
        {
            if (parentOfDeleteNode->left == deleteNode)      //删除节点是父节点的左子节点，且删除节点只有左子树
                parentOfDeleteNode->left = deleteNode->left; //把父节点的left指向deleteNode的左子节点
            if (parentOfDeleteNode->right == deleteNode)
                parentOfDeleteNode->right = deleteNode->left;
        }
        else if (deleteNode->right != NULL)
        {
            if (parentOfDeleteNode->left == deleteNode) //
                parentOfDeleteNode->left = deleteNode->right;
            if (parentOfDeleteNode->right == deleteNode)
                parentOfDeleteNode->right = deleteNode->right;
        }
    }
    else if (deleteNode->left != NULL || deleteNode->right != NULL) // case：3 删除节点有左子树和右子树
    {
        Tree *replaceNode = maxValueOfBinaryTree(deleteNode->left);
        //找到删除节点的左子树的最右节点（对应左子树的最大键值）作为替代节点，替代节点的键值与删除节点的键值是相邻的，
        Tree *parentOfReplaceNode = parentNodeOfBinaryTreeNode(replaceNode, *root); //获取替代节点的父节点
        if (*root == deleteNode)
        {
            parentOfReplaceNode->right = replaceNode->left;
            replaceNode->left = (*root)->left;
            replaceNode->right = (*root)->right;
            (*root) = replaceNode;
        }
        else if (parentOfDeleteNode->left == deleteNode) //删除节点是其父节点的左子节点
        {
            parentOfDeleteNode->left = replaceNode; //删除节点的父节点left指向替代节点
            replaceNode->left = deleteNode->left;
            if (parentOfReplaceNode != deleteNode)
            {
                replaceNode->right = deleteNode->right;
                //替代节点右子树指向删除节点右子树（如果替代节点父节点就是删除节点，deleteNode->right就是该替代节点，造成后面子树丢失；parentOfReplaceNode->right也没有意义）
                parentOfReplaceNode->right = replaceNode->left;
            }
            else if (parentOfReplaceNode == deleteNode)
                replaceNode->right = deleteNode->right->left; //替换节点的右子树指向了替换节点的左子树，看树图很容易理解
        }
        else if (parentOfDeleteNode->right == deleteNode) //删除节点是父节点的右子节点
        {
            parentOfDeleteNode->right = replaceNode; //删除节点的父节点right指向左子树最大键值对应节点
            replaceNode->right = deleteNode->right;
            if (parentOfReplaceNode != deleteNode)
            {
                replaceNode->left = replaceNode->left;
                parentOfReplaceNode->right = replaceNode->left;
            }
            else if (parentOfReplaceNode == deleteNode)
                replaceNode->left = replaceNode->left->left;
        }
    }
    free(deleteNode);
}

 8 中序遍历代码以及查找指定节点代码

Tree *searchTreeNode(Tree *root, int value) //搜索二叉排序树含指定数据的节点
{
    if (root == NULL)
        return NULL;
    if (root->data > value)
        return searchTreeNode(root->left, value);
    if (root->data < value)
        return searchTreeNode(root->right, value);
    else
        return root;
}
void inOrderList(Tree *root)//中序遍历
{
    if (root == NULL)
        return;
    inOrderList(root->left);
    printf("%d->", root->data);
    inOrderList(root->right);
}

9 函数测试与运行结果

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main()
{
    int array[] = {2, 6, 9, 8, 12, 3, 5, 4, 0, -66, 1, -88};
    Tree root = {2, NULL, NULL};
    Tree *pointer = &root;
    for (int i = 1; i < sizeof(array) / sizeof(array[0]); i++)
    {
        Tree *node = createBinarySortTreeNode(array[i]);
        insertBinarySortTreeNode(node, &pointer);//插入节点
    }
    inOrderList(&root); //二叉排序树中序遍历
    puts("");
    Tree *maxNode = maxValueOfBinaryTree(&root);//最大键值节点查找
    printf("the maxValueNode:{data:%d left:%p right:%p}\n", maxNode->data, maxNode->left, maxNode->right);
    Tree *minNode = minValueOfBinaryTree(&root);//最小键值节点查找
    printf("the minValueNode:{data:%d left:%p right:%p}\n", minNode->data, minNode->left, minNode->right);
    Tree *searchNode = searchTreeNode(&root, 6);//查找指定节点
    printf("searchNode->{data:%d left:%p right:%p}\n", searchNode->data, searchNode->left, searchNode->right);
    Tree *parentNode = parentNodeOfBinaryTreeNode(searchNode, &root);//指定节点的父节点查找
    printf("parentNode->{data:%d left:%p right:%p} searchNode:%p\n", parentNode->data, parentNode->left, parentNode->right, searchNode);
    //如果测试删除root节点，需要把上行printf里面的parentNode的data去掉，因为是NULL，无法解引用
    Tree *pointer2 = &root;
    deleteBinarySortTreeNode(searchNode, &pointer2);//删除指定节点
    printf("删除节点searchNode节点后:  ");
    inOrderList(pointer2);//中序遍历
    return 0;
}

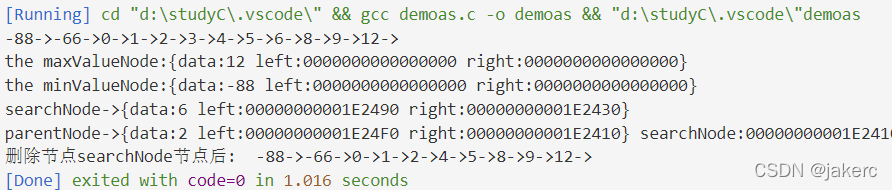
 运行结果如下：

 

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
quartz.JobPersistenceException: Couldn‘t retrieve trigger
Android framework interface_cast 模板方法分析
win10linux子系统2018,Windows 10 使用 Kali Linux子系统
Springboot项目实战1
java实现文件加密解密
将数据库中取出的blob显示为图片
关于alpine如何制作JDK镜像
带你深入了解Docker镜像，看完之后你也能像庖丁解牛一样熟练
网络安全入门学习第九课——计算机网络基础_公网地址和私网地址范围
Unity 使用贝塞尔曲线实现抛物线运动
;