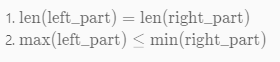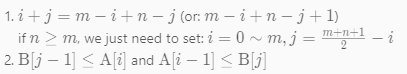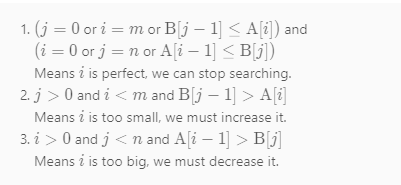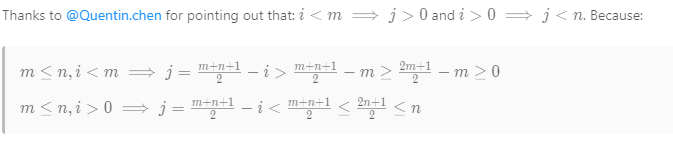1. Array
(1) 27. Remove Element(Easy)
给定数组nums和值val,在适当位置删除该值的所有实例并返回新长度。
思路:
不需要使用排序,如果等于该值,则将n-1的值赋给i,然后n = n - 1
def removeElement(self, nums, val):
"""
:type nums: List[int]
:type val: int
:rtype: int
"""
i = 0
n = len(nums)
while(i<n):
if (nums[i] ==val):
nums[i]= nums[n-1]
n -=1
else:
i+=1
return n
(2) 26. Remove Duplicates from Sorted Array(Easy)
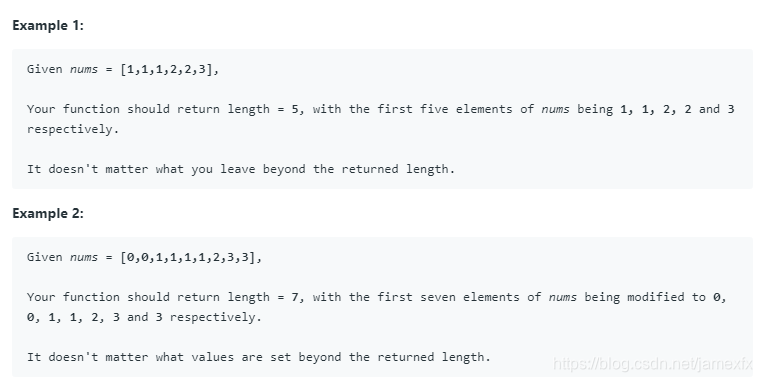
给定排序的数组nums,就地删除重复项,使每个元素只出现一次并返回新的长度。
不要为另一个数组分配额外的空间,必须通过使用O(1)额外内存修改输入数组来实现此目的。
思路:
使用del
def removeDuplicates(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
i = 0
while i < len(nums)-1:
if nums[i+1] == nums[i]:
del nums[i+1]
else:
i += 1
return len(nums)
(3) 80. Remove Duplicates from Sorted Array II(Medium)
给定排序的数组nums,就地删除重复项,使重复项最多出现两次并返回新的长度。
思路:
使用单层循环,使用nums[j]>nums[i-2]来判断
def removeDuplicates(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
i = 0
for n in range(len(nums)):
if i<2 or nums[n]>nums[i-2]:
nums[i] = nums[n]
i +=1
return i
(4) 277. Find the Celebrity
如果一个人A是名人,那么其他的n-1个人都认识A,而且A不认识其他的n-1个人。这题的目标是要从n个人中找出其中的名人,如果没有,则告知其中没有名人。我们可以调用knows(a,b)函数来询问a是否认识b,而我们要尽量少调用这个函数。
思路:
如果我们从n个人中任意挑两个人a,b出来,询问啊是否认识b,那么只有两种情况:
(1)a认识b:那么a肯定不是名人。
(2)b认识a:那么b肯定不是名人。
所以任何一种情况,我们都可以排除掉2个人中的1一个人。如果我们不断地重复的这个过程,直到只剩下一个人,那么我们会做n-1次对比。而剩下这个人是唯一可能成为名人的人,那么我们需要询问剩下的n-1个人是否认识他,也需要询问他是否认识剩下的n-1个人。
因此我们一共需要询问3(n-1)次——时间复杂度为O(n)。(其中n个人中不可能存在两个名人,可证)
def findCelebrity(self,n):
if n ==0:
return -1
curr_stay = 0
for i in range(1,n):
if know(curr_stay,i):
curr_stay = i
for i in range(0,n):
if curr_stay == i:
cotinue
if know(curr_stay,i):
return -1
if not know(i,curr_stay)
return -1
return curr_stay
(5) 189. Rotate Array
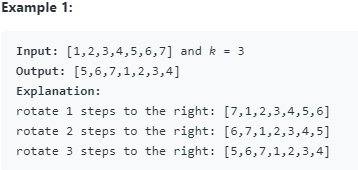
给定一个数组,将数组向右旋转k步,其中k为非负数,使用O(1)的空间,无需返回,直接数组上改动
思路:
Original List : 1 2 3 4 5 6 7
After reversing all numbers: 7 6 5 4 3 2 1
After reversing first k numbers : 5 6 7 4 3 2 1
After revering last n-k numbers : 5 6 7 1 2 3 4 --> Result
先全部reverse,然后前K个reverse,后面n-k个reverse
def rotate(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: void Do not return anything, modify nums in-place instead.
"""
def reverse(start,end,nums):
while(start<end):
temp = nums[end]
nums[end] = nums[start]
nums[start] = temp
start +=1
end -=1
return nums
k = k %len(nums)
nums = reverse(0,len(nums)-1,nums)
nums = reverse(0,k-1,nums)
nums = reverse(k,len(nums)-1,nums)
(6) 41. First Missing Positive(Hard)
给定未排序的整数数组,找到最小的缺失正整数。您的算法应该在O(n)时间运行并使用恒定的额外空间。
思路:
1、需要时间复杂度为n
2、并且是寻找的最小的缺失正整数
3、首先将num[i] 放置在 num[num[i]-1]上,首要要保证num[i]-1<len(num)
4、使用while知道num[i]放到适当的位置,因为for循环,i会直接跳过,如果不用while
5、找到第一个 nums[i] 不等于i+1,如果没有,返回 len +1
def firstMissingPositive(self,nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(len(nums)):
while 0<=nums[i]-1<len(nums) and nums[nums[i]-1] !=nums[i]:
temp = nums[i]-1
nums[temp],nums[i] = nums[i],nums[temp]
for i in range(len(nums)):
if nums[i]!=i+1:
return i+1
return len(nums)+1
(7) 299. Bulls and Cows(Medium)
给定两个等长的字符串,字符串中只包含数字,求两个字符串中的bulls和cows。其中,bulls表示在字符串同一位置的数值相同的数字的个数。cows表示,guess中的数字在secret中出现了,但是处在不正确的位置上的数字的个数。
1,每次给出的数字可能是重复的(跟一般猜数字不同);2,题目没说是每次四个数字,只说secret和guess一样长。
def getHint(self, secret, guess):
bulls = sum(i==j for i,j in zip(secret,guess))
bows = sum(min(secret.count(x),guess.count(x)) for x in set(guess)) - bulls
return '%dA%dB' %(bulls,bows)
(8) 134 .Gas Station(Medium)
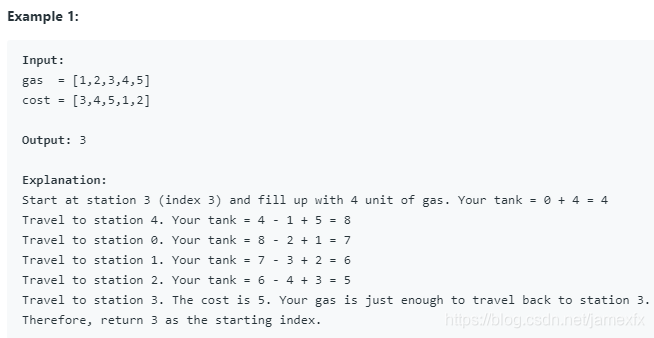
在一个圈子路线里面有N个汽油站,i站的汽油有gas[i]汽油。现在有一辆无限容量的车,它从i站开到(i+1)需要耗费cost[i]汽油。如果这辆车可以走完这个圈,那么返回这个车的起点,否者返回-1.
思路:
1、如果gas的总和大于或等于cost的总和,必然存在一种路线使得走完整个圈子。
2、假设当前剩余的油量为diff,若达到站点i的的剩余油量小于0,则将设置起始站点设为i;另外设置所有站点的剩余油量为total,当total小于0,则不能环绕,否则可以
def canCompleteCircuit(self,gas,cost):
"""
:type gas: List[int]
:type cost: List[int]
:rtype: int
"""
if sum(gas)<sum(cost):
return -1
index = 0
diff = 0
for i in range(len(gas)):
if gas[i]+dif <cost[i]:
index = i +1
diff = 0
else:
diff += gas[i]-cost[i]
return index
(9) 118. Pascal’s Triangle(Easy)(很少考)
给定非负整数numRows,生成Pascal三角形的第一个numRows。
Input: 5
Output:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
def generate(self, numRows):
"""
:type numRows: int
:rtype: List[List[int]]
"""
total = []
if numRows == 0:
return total
total =[[1]]
if numRows==1:
return total
total = [[1],[1,1]]
if numRows==2:
return total
for i in range(3,numRows+1):
total.append([])
for j in range(i):
if j ==0 or j == i-1:
total[-1].append(1)
else:
total[-1].append(total[i-2][j-1]+total[i-2][j])
return total
(10) 119. Pascal’s Triangle II(Easy)(很少考)
给定非负索引k,其中k≤33,返回Pascal三角形的第k个索引行。
思路:
1、使用递归,直到递归到那一层
def getRow(self, rowIndex):
"""
:type rowIndex: int
:rtype: List[int]
"""
if rowIndex == 0:
return [1]
if rowIndex == 1:
return [1,1]
prerow = self.getRow(rowIndex-1)
return [1]+[prerow[i]+prerow[i+1] for i in range(len(prerow)-1)]+[1]
(11) 274. H-Index(Medium)
给定研究者的一系列引用(每个引用是一个非负整数),写一个函数来计算研究者的h指数。
H指数(H index)是一个混合量化指标,可用于评估研究人员的学术产出数量与学术产出水平
可以按照如下方法确定某人的H指数:
将其发表的所有SCI论文按被引次数从高到低排序;
从前往后查找排序后的列表,直到某篇论文的序号大于该论文被引次数。所得序号减一即为H指数。
h指数是指他至多有h篇论文分别被引用了至少h次
思路:
解法1: 先将数组排序,T:O(nlogn), S:O(1)。然后对于每个引用次数,比较大于该引用次数的文章,取引用次数和文章数的最小值,即 Math.min(citations.length-i, citations[i]),并更新 level,取最大值。排好序之后可以用二分查找进行遍历,这样速度会更快。
h指数是指他至多有h篇论文分别被引用了至少h次
解法2: Counting sort,T:O(n), S:O(n)。使用一个大小为 n+1 的数组count统计引用数,对于count[i]表示的是引用数为 i 的文章数量。从后往前遍历数组,当满足 count[i] >= i 时,i 就是 h 因子,返回即可,否则返回0。
为什么要从后面开始遍历? 为什么 count[i] >= i 时就返回?
一方面引用数引用数大于 i-1 的数量是i-1及之后的累加,必须从后往前遍历。另一方面,h 因子要求尽可能取最大值,而 h 因子最可能出现最大值的地方在后面,往前值只会越来越小,能尽快返回就尽快返回,所以一遇到 count[i] >= i 就返回。(count[i-1]代表大于i-1的个数有多少)
def hIndex(self, citations):
"""
:type citations: List[int]
:rtype: int
"""
n = len(citations)
count = [0]*(n+1)
for i in range(n):
if citations[i]>=n:
count[n]+=1
else:
count[citations[i]] +=1
for i in range(n,0,-1):
if count[i]>=i:
return i
count[i-1] +=count[i]#count[i-1]代表大于i-1的个数有多少
return 0
(12) 275. H-Index II(Medium)(Binary Search)
给定一个按升序排序的引文数组(每个引用是非负整数),编写一个函数来计算研究者的h指数。
思路:
274题的拓展。输入的数组是有序的,让我们优化算法。提示(现在题目中没有提示了):O(logn)。显然使用二分法。
def hIndex(self, citations):
"""
:type citations: List[int]
:rtype: int
"""
n = len(citations)
left = 0
right = n-1
while left<=right:
middle = (left+right)//2
if citations[middle] >=n-middle:
right = middle-1
else:
left = middle+1
return n-left
(13) 243. Shortest Word Distance(Easy)
给一个string的数组,里面有word1和word2两个词,要求返回这两个词之间的最短距离。
思路:
给定两个指针,如果这两个都不为空,求最小值。
def shortestDistance(self, words, word1,word2):
"""
:type words: List[str]
:type word1: str
:type word2: str
:rtype: int
"""
p1 = -1
p2 = -1
result = len(words)
for i in range(len(words)):
if words[i] == word1:
p1 = i
elif word[i] == word2:
p2 = i
if p1!=-1 and p2!=-1:
result = min(result,abs(p2-p1))
return result
(14) 217. Contains Duplicate
给定一个整数数组,查找数组是否包含任何重复项。 如果数组中任何值至少出现两次,则函数应返回true,如果每个元素都不相同,则返回false。
思路:
可以巧妙的利用len 和 set
set底层实现也是用了hash和eq函数
def containsDuplicate(self,nums):
"""
:type nums: List[int]
:rtype: bool
"""
return len(nums)!=len(set(nums))
(15) 219. Contains Duplicate II(Easy)(很少考)
给定一个整数数组和一个整数k,找出数组中是否存在两个不同的索引i和j,使得nums [i] = nums [j]并且i和j之间的绝对差值最多为k
思路:
使用字典存储最大的index,判断是否有重复的元素时,需要判断两者之间是否不大于k
def containsNearbyDuplicate(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: bool
"""
dict = {}
for i,v in enumerate(nums):
if v in dict and i - dict[v] <=k:
return True
else:
dict[v] = i
return False
(16) 220. Contains Duplicate III(很少考)
给定一个整数数组,找出数组中是否有两个不同的索引i和j,使得nums [i]和nums [j]之间的绝对差值最大为t,i和j之间的绝对差值最大ķ。
思路:
如果: | nums[i] - nums[j] | <= t 式a
等价: | nums[i] / t - nums[j] / t | <= 1 式b
推出: | floor(nums[i] / t) - floor(nums[j] / t) | <= 1 式c
等价: floor(nums[j] / t) ∈ {floor(nums[i] / t) - 1, floor(nums[i] / t), floor(nums[i] / t) + 1} 式d
其中式b是式c的充分非必要条件,因为逆否命题与原命题等价,所以:
如果: floor(nums[j] / t) ∉ {floor(nums[i] / t) - 1, floor(nums[i] / t), floor(nums[i] / t) + 1} 非d
floor 指上界
def containsNearbyAlmostDuplicate(self, nums, k, t):
"""
:type nums: List[int]
:type k: int
:type t: int
:rtype: bool
"""
# 检验数据合法性
if k < 1 or t < 0:
return False
# 这里采用有序字典,它是dict的一个继承子类,按照元素输入顺序进行排序
dic = collections.OrderedDict()
for n in nums:
# 注意判断t是否为0
key = n if not t else n // t
for m in (dic.get(key - 1), dic.get(key), dic.get(key + 1)):
# 如果找到一个数满足条件一,返回
if m is not None and abs(n - m) <= t:
return True
if len(dic) == k:
# 维持字典大小为k,如果超过,删除first;函数原型:dict.popitem(last=False),不加参数表示随机从头尾删除一个
dic.popitem(False)
# 加入新数
dic[key] = n
return False
(17) 55. Jump Game(Medium)
跳棋,给一个list,查看能否到达最后一个
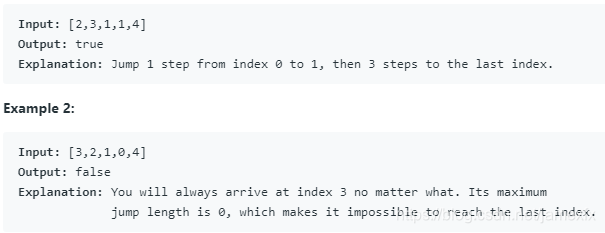
给定一个非负整数数组,您最初定位在数组的第一个索引处。 数组中的每个元素表示该位置的最大跳转长度。 确定您是否能够到达最后一个索引。
思路:
给个判断条件i<cur
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
cur = 0
for i in range(len(nums)):
if i>cur:
return False
cur = max(i+nums[i],cur)
return True
(18) 45. Jump Game II(Hard)
每次可以向后面跳跃的格子数等于当前的点数。求最少需要多少步就能调大最后的格子。
Input: [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2.
Jump 1 step from index 0 to 1, then 3 steps to the last index.
思路:
要记录当前一跳所能到达的最远距离cur、上一跳所能到达的最远距离last,和当前所使用跳数
如果i<last,则表示从last这个位置可以直接到达i的位置,res就不需要加1;如果i>last,则表示从last到不了该位置,这一步就是必须的,res就要加1。同时要更新last的值。而cur记录当前位置可以到达的最大位置,用以更新last的值。
def jump(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# cur表示当前步能到达的最远位置
cur=0
# last表示上一次能到达的最远位置
last = 0
# 记录总共跳了多少步
res = 0
for i in range(len(nums)):
if i>last:
last = cur
res +=1
if cur<i+nums[i]:
cur = i+nums[i]
return res if cur>=len(nums)-1 else 0
(19) 121. Best Time to Buy and Sell Stock(Easy)
假设您有一个数组,其中第i个元素是第i天给定股票的价格。 如果您只被允许完成最多一笔交易(即买入并卖出一股股票),请设计一个算法以找到最大利润。
思路:
定义一个i之前的最小值,定义一个到i最大的sum
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
min_p = float('inf')
sum_o = 0
for i in range(len(prices)):
min_p = min(min_p,prices[i])
p = prices[i]-min_p
sum_o = max(p,sum_o)
return sum_o
(20) 122. Best Time to Buy and Sell Stock II(Easy)
设计算法以找到最大利润。您可以根据需要完成尽可能多的交易(即,多次买入并卖出一股股票)。
您不得同时进行多笔交易(即,您必须在再次购买之前卖出股票)。
思路:
1、可以找到谷峰和低洼,然后相减
2、完全可以不用理谷峰和低洼,如果值递增的只要前后相减就可以了,避免了找谷峰和低洼
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
total = 0;
for i in range(len(prices)-1):
if prices[i+1]>prices[i]:
total += prices[i+1]-prices[i]
return total
(21) 123. Best Time to Buy and Sell Stock III(Hard)
假设您有一个数组,其中第i个元素是第i天给定股票的价格。 设计算法以找到最大利润。您最多可以完成两笔交易。
思路:
使用DP
计算某一天极其之前所有时间内的最大利益
计算某一天极其之后所有时间内价格的最利益
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
#使用DP好了,另一个实在看不懂
n = len(prices)
if n ==0:
return 0
p1 = [0]*n
p2 = [0]*n
##计算某一天极其之前所有时间内的最大利益
min_price = prices[0]
for i in range(1,n):
min_price = min(prices[i],min_price)
p1[i] = max(p1[i-1],prices[i]-min_price)
##计算某一天极其之后所有时间内价格的最利益
max_price = prices[-1]
for i in range(n-2,-1,-1):
max_price = max(prices[i],max_price)
p2[i] = max(p2[i+1],max_price-prices[i])
ans = 0
## 计算最大收益
for i in range(n):
ans = max(ans,p1[i]+p2[i])
return ans
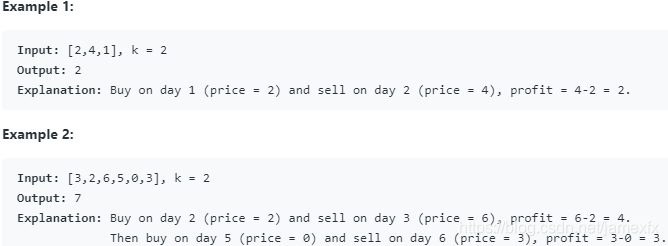
(22) 188. Best Time to Buy and Sell Stock IV(Hard)
假设您有一个数组,其中第i个元素是第i天给定股票的价格。
设计算法以找到最大利润。您最多可以完成k笔交易。
您不得同时进行多笔交易(即,您必须在再次购买之前卖出股票)。
思路:
DP解决
使用两个list,一个global,一个local
1、一个是当前到达第i天可以最多进行j次交易,最好的利润是多少(global[i][j])
2、另一个是当前到达第i天,最多可进行j次交易,并且最后一次交易在当天卖出的最好的利润是多少(local[j])(看代码中的英文解释会更好一点)
#判断是否在边界
#如果k>=n/2足够大,那么这个问题就会变成问题Ⅱ了
def maxProfit(self, k, prices):
"""
:type k: int
:type prices: List[int]
:rtype: int
"""
##判断是否在边界
n = len(prices)
if k<=0 or n ==0:
return 0
##如果k足够大,那么这个问题就会变成问题Ⅱ了
if k>=n/2:
result = 0
for i in range(1,n):
if prices[i]-prices[i-1]>0:
result +=prices[i] - prices[i-1]
return result
global_profit = [[0]*n for _ in range(k+1)]
for i in range(1,k+1):
local_profit = [0]*n
for j in range(1,n):
profit = prices[j] - prices[j-1]
#We have made max profit with (i - 1) transations in (j - 1) days.
#For the last transation, we buy stock on day (j - 1) and sell it on day j.
# We have made profit in (j - 1) days.
# We want to cancel the day (j - 1) sale and sell it on day j.
local_profit[j] = max(global_profit[i-1][j-1]+max(profit,0),local_profit[j-1]+profit)
global_profit[i][j] = max(local_profit[j],global_profit[i][j-1])
return global_profit[k][n-1]
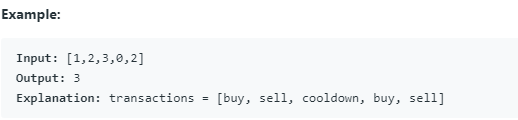
(23) 309. Best Time to Buy and Sell Stock with Cooldown(Medium)
设计算法以找到最大利润。您可以通过以下限制完成任意数量的交易(即,多次买入并卖出一股股票):
您不得同时进行多笔交易(即,您必须在再次购买之前卖出股票)。
在您出售股票后,您无法在第二天购买股票。 (即冷却1天)
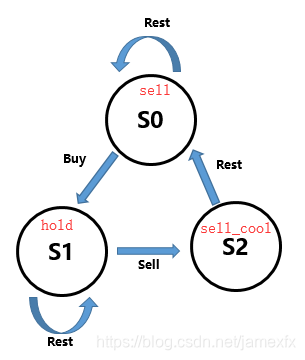
思路:
可以使用状态机轻松求解
s0[i] = max(s0[i-1], s2[i-1])
s1[i] = max(s1[i-1], s0[i-1] - price[i])
s2[i] = s1[i-1] + price[i]
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
#记得时‘-inf’ 和sell是0,另外两个都未知
sell,sell_cooldown,hold = 0,float('-inf'),float('-inf')
for p in prices:
hold,sell,sell_cooldown = max(hold,sell-p),max(sell,sell_cooldown),hold+p
return max(sell,sell_cooldown)
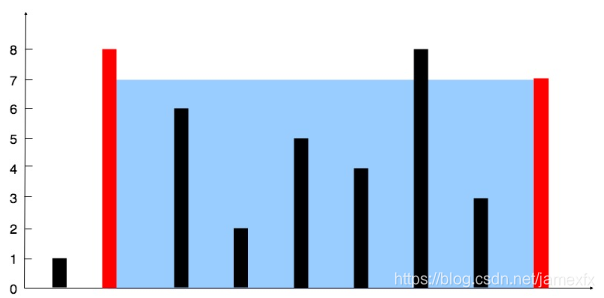
(24) 11. Container With Most Water (Medium)
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
思路:首先先从两边开始,确定最大的宽,然后再慢慢缩小
def maxArea(self, height):
"""
:type height: List[int]
:rtype: int
"""
i= 0
j = len(height)-1
max = 0
while(i!=j):
if height[i]<height[j]:
max = height[i]*(j-i) if height[i]*(j-i)>max else max
i+=1
else:
max = height[j]*(j-i) if height[j]*(j-i)>max else max
j-=1
return max
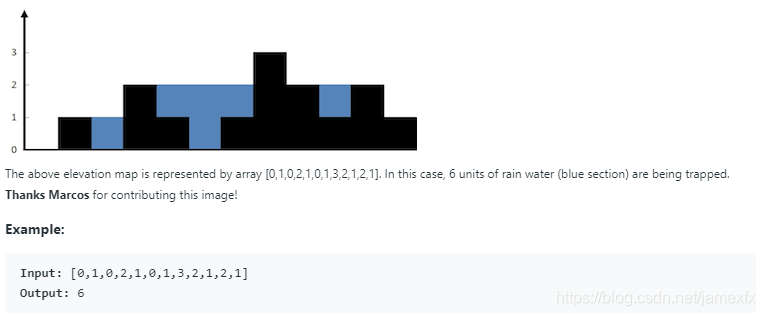
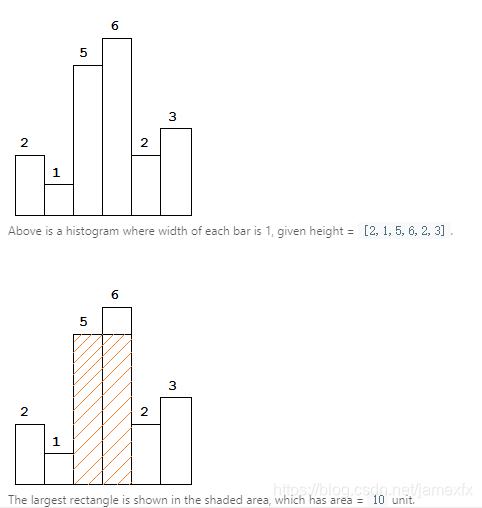
(25) 42. Trapping Rain Water(Hard)
给定n个非负整数表示每个柱的宽度为1的高程图,计算下雨后能够捕获的水量。
思路:
(1)从左向右进行扫描,获取每个位置的左边最高的边。
(2)从右向左进行扫描,获取每个位置的右边最高的边。
(3)再遍历一边,找出left[i]和right[i]最小的一个,减去当前值,累加
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
if len(height)==0:return 0
left = [0]*len(height)
left[0] = height[0]
for i in range(1,len(height)):
left[i] = max(left[i-1],height[i])
right = [0]*len(height)
right[-1] = height[-1]
for i in range(len(height)-2,-1,-1):
right[i] = max(right[i+1],height[i])
res = 0
for i in range(len(height)):
res += min(left[i],right[i])-height[i]
return res
(26) 334. Increasing Triplet Subsequence(Medium)
给定未排序的数组返回是否在数组中存在增加的长度为3的子序列。 正式的功能应该
Return true if there exists i, j, k
such that arr[i] < arr[j] < arr[k] given 0 ≤ i < j < k ≤ n-1 else return false.
O(n) time complexity and O(1) space complexity
def increasingTriplet(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
first = second = float('inf')
for n in nums:
if n<=first:
first = n
elif n<=second:
second = n
else:
return True
return False
(27) 128. Longest Consecutive Sequence(Hard)
给定未排序的整数数组,找到最长连续元素序列的长度。
思路:
在for循环中加入一些判断达到O(n)的复杂度
首先判断元素是不是最小的,然后再开始+1操作,计算长度
def longestConsecutive(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
longest = 0
nums = set(nums)
for i in nums:
if i-1 not in nums:
current_num = i
current_long = 1
while current_num+1 in nums:
current_num +=1
current_long +=1
longest = max(longest,current_long)
return longest
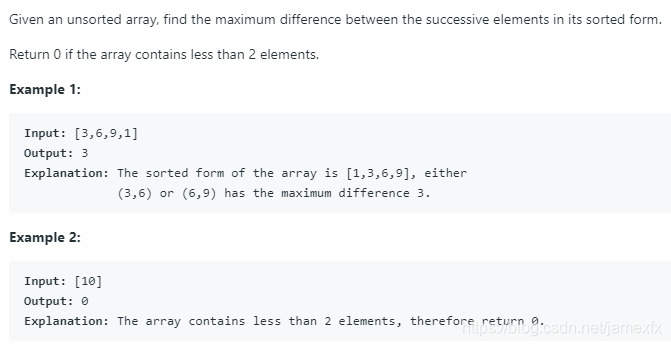
(28) 164. Maximum Gap(Hard)(桶排序)
给定未排序的数组,找到其排序形式中的连续元素之间的最大差异。 如果数组包含少于2个元素,则返回0。(尝试在线性时间/空间中解决它。)
思路:
解题思路
由于需要线性,并且假定是整数,使用桶排序
1、如果数组中数字小于2或者最大最小值相等,return 0
2、向上取整(math.ceil()),得到桶的大小(最大值-最小值)/(数组长度-1)
(差值不小于(最大值-最小值)/(数组长度-1))
3、得到多少个桶(最大值-最小值)/(桶的大小+1)
4、循环将元素放入桶中(i = bucket[(n-a)//size]),只需记录最大最小值
5、不同桶之间的最大最小值,就是候选值
def maximumGap(self, num):
"""
:type nums: List[int]
:rtype: int
"""
if len(num) < 2 or min(num) == max(num):
return 0
a, b = min(num), max(num)
size = (b-a)//(len(num)-1) or 1
bucket = [[None, None] for _ in range((b-a)//size+1)]
for n in num:
b = bucket[(n-a)//size]
b[0] = n if b[0] is None else min(b[0], n)
b[1] = n if b[1] is None else max(b[1], n)
bucket = [b for b in bucket if b[0] is not None]
return max(bucket[i][0]-bucket[i-1][1] for i in range(1, len(bucket)))
(29) 287. Find the Duplicate Number(Medium)
给定包含n + 1个整数的数组nums,其中每个整数在1和n之间(包括1和n),证明必须存在至少一个重复的数字。假设只有一个重复的数字,找到重复的数字.(可能数组中含有多个重复数字)
1、您不能修改数组(假设该数组是只读的)。
2、您必须仅使用常量O(1)额外空间。
3、您的运行时复杂度应小于O(n2)。
4、 数组中只有一个重复的数字,但它可以重复多次。
思路:
方法一:sorted之后,用前后是否一样 时间复杂度:O(nlogn) 空间复杂度:O(1)
方法二:使用set() 时间复杂度:O(n) 空间复杂度:O(n)
方法三:映射找环法
假设数组中没有重复,那我们可以做到这么一点,就是将数组的下标和1到n每一个数一对一的映射起来。比如数组是213,则映射关系为0->2, 1->1, 2->3。假设这个一对一映射关系是一个函数f(n),其中n是下标,f(n)是映射到的数。如果我们从下标为0出发,根据这个函数计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推,直到下标超界。(由于我们这题是一定存在环,所以不用这个判断)实际上可以产生一个类似链表一样的序列。比如在这个例子中有两个下标的序列,0->2->3。
但如果有重复的话,这中间就会产生多对一的映射,比如数组2131,则映射关系为0->2, {1,3}->1, 2->3。这样,我们推演的序列就一定会有环路了,这里下标的序列是0->2->3->1->1->1->1->…,而环的起点就是重复的数。
所以该题实际上就是找环路起点的题,和142. Linked List Cycle II一样。
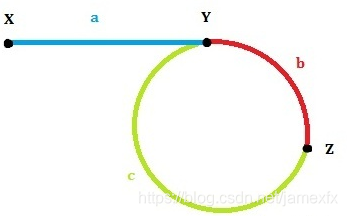
第一次相遇时slow走过的距离:a+b,fast走过的距离:a+b+c+b。
因为fast的速度是slow的两倍,所以fast走的距离是slow的两倍,有 2(a+b) = a+b+c+b,
可以得到a=c(这个结论很重要!)。
def findDuplicate(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
slow = nums[0]
fast = nums[0]
while True:
slow = nums[slow]
fast = nums[nums[fast]]
if slow == fast:
slow = nums[0]
while slow !=fast:
slow = nums[slow]
fast = nums[fast]
return slow
(30) 135. Candy(Hard)(很少考)
几个小孩站一排,每个小孩有个等级值,现在给小孩发糖,发的时候要遵守2个规则:(1)每个小孩至少一颗糖(2)两个相邻的小孩中,等级大的小孩一定比等级小的小孩糖多,求发糖的数目的最小值。对于等级序列[1, 2, 2]来说,发糖数目最小值为4,发糖序列为[1, 2, 1]。
思路:
1、初始化所有小孩糖数目为1
2、从前往后扫描,如果第i个小孩等级比第i-1个高,那么i的糖数目等于i-1的糖数目+1
3、从后往前扫描,如果第i个的小孩的等级比i+1个小孩高,但是糖的数目却小或者相等,那么i的糖数目等于i+1的糖数目
(第一遍,保证了每一点比他左边candy更多(如果得分更高的话)。第二遍,保证每一点比他右边candy更多(如果得分更高的话),同时也会保证比他左边的candy更多,因为当前位置的candy只增不减。)
def candy(self, ratings):
"""
:type ratings: List[int]
:rtype: int
"""
candy = [1 for i in range(len(ratings))]
for i in range(1,len(ratings)):
if ratings[i]>ratings[i-1]:
candy[i] =candy[i-1]+1
for i in range(len(ratings)-2,-1,-1):
if ratings[i]>ratings[i+1]and candy[i]<=candy[i+1]:
candy[i] =candy[i+1]+1
return sum(candy)
提高
(31)4. Median of Two Sorted Arrays(Hard)
有两个排序的数组nums1和nums2分别为m和n。 找到两个排序数组的中位数。总运行时间复杂度应为O(log(m + n))。
您可以假设nums1和nums2不能都为空。
思路:
我们可以假设:
所以我们就可以确定:
(n>m? 因为0≤i≤m并且j= (m+n+1)/2 -i 如果n<m,j就会是负数)
对于边界的 i=0,i=m,j=0,j=n where A[i-1],B[j-1],A[i],B[j] 不存在,如果处理?
本来需要对比两个不等式,如果其中一个不存在,那么那个不等式就不用对比了,就只用对比另一个就好了,例如i = 0 ,则A[i-1]不存在,所以我们就不需要对比A[i-1]<=B[j]
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
m,n = len(nums1),len(nums2)
if n<m:
m,n,nums1,nums2 = n,m,nums2,nums1
imin,imax,middle = 0,m,int((n+m+1)/2)
while imin<=imax:
i = int((imin+imax)/2)
j = middle - i
if i < m and nums1[i]<nums2[j-1]:
# i is too small, must increase it
imin = i + 1
elif i>0 and nums1[i-1]>nums2[j]:
# i is too big, must decrease it
imax = i - 1
else:
if j == 0:
max_of_left = nums1[i-1]
elif i == 0:
max_of_left = nums2[j-1]
else:
max_of_left = max(nums1[i-1],nums2[j-1])
if (n+m)%2 == 1:
return max_of_left
if j ==n:
min_of_right = nums1[i]
elif i == m:
min_of_right = nums2[j]
else:
min_of_right = min(nums1[i],nums2[j])
return (max_of_left+min_of_right)/2.0
(32)289. Game of Life(Medium)
给定具有m×n个单元的板,每个单元具有初始状态live(1)或dead(0)。每个单元格使用以下四个规则(取自上述维基百科文章)与其八个邻居(水平,垂直,对角线)进行交互
1任何活的邻居少于两个的活细胞都会死亡,好像是由人口不足造成的。
2任何有两三个活邻居的活细胞都会留在下一代。
3任何有三个以上活着的邻居的活细胞都会死亡,好像人口过多一样
4具有正好三个活邻居的任何死细胞变成活细胞,就好像通过繁殖一样
编写一个函数来计算给定其当前状态的电路板的下一个状态(在一次更新之后)。通过将上述规则同时应用于当前状态中的每个细胞来创建下一个状态,其中出生和死亡同时发生
你能在原地解决吗?请记住,电路板需要同时更新:您不能先更新某些单元格,然后使用更新的值更新其他单元格
思路:
首先定义8个方向的向量
然后使用双重循环遍历,统计某个点周围活细胞
最后利用规则进行更新
为了能够原地更新,先把更新的用-1和2来代替,再用一个双循环进行更新
def gameOfLife(self, board):
"""
:type board: List[List[int]]
:rtype: None Do not return anything, modify board in-place instead.
"""
# Neighbors array to find 8 neighboring cells for a given cell
neighbors = [(1,0), (1,-1), (0,-1), (-1,-1), (-1,0), (-1,1), (0,1), (1,1)]
rows = len(board)
cols = len(board[0])
# Iterate through board cell by cell.
for row in range(rows):
for col in range(cols):
# For each cell count the number of live neighbors.
live_neighbors = 0
for neighbor in neighbors:
# row and column of the neighboring cell
r = (row + neighbor[0])
c = (col + neighbor[1])
# Check the validity of the neighboring cell and if it was originally a live cell.
if (r < rows and r >= 0) and (c < cols and c >= 0) and abs(board[r][c]) == 1:
live_neighbors += 1
# Rule 1 or Rule 3
if board[row][col] == 1 and (live_neighbors < 2 or live_neighbors > 3):
# -1 signifies the cell is now dead but originally was live.
board[row][col] = -1
# Rule 4
if board[row][col] == 0 and live_neighbors == 3:
# 2 signifies the cell is now live but was originally dead.
board[row][col] = 2
# Get the final representation for the newly updated board.
for row in range(rows):
for col in range(cols):
if board[row][col] > 0:
board[row][col] = 1
else:
board[row][col] = 0
Interval
(33)56. Merge Intervals(Medium)
给定间隔的集合,合并所有重叠的间隔。
思路:
要使用sorted(key = lambda)函数
for k in sorted(intervals,key = lambda i:i.start):
def merge(self, intervals):
"""
:type intervals: List[Interval]
:rtype: List[Interval]
"""
out = []
for k in sorted(intervals,key = lambda i:i.start):
if out and k.start<=out[-1].end:
out[-1].end = max(out[-1].end,k.end)
else:
out.append(k)
return out
(34)57. Insert Interval(Hard)
给定一组非重叠间隔,在间隔中插入新间隔(必要时合并)。 您可以假设间隔最初是根据其开始时间排序的。
Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].
思路:主要是想清楚判断条件,要新建一个数组用来存储
如果插入的数组在两个数组之间,则要判断谁的start、end小和大
def insert(self, intervals, newInterval):
"""
:type intervals: List[Interval]
:type newInterval: Interval
:rtype: List[Interval]
"""
i =0
all =[]
start = newInterval.start
end = newInterval.end
while i<len(intervals):
if intervals[i].end>=start:
if intervals[i].start>end:
break
start = min(start,intervals[i].start)
end = max(end,intervals[i].end)
else:
all.append(intervals[i])
i+=1
all.append(Interval(start,end))
all += intervals[i:]
return all
(35)LeetCode 252. Meeting Rooms(Easy)
给定一系列会议时间间隔,包括开始和结束时间[[s1,e1],[s2,e2],…](si <ei),确定一个人是否可以参加所有会议.
For example,
Given [[0, 30],[5, 10],[15, 20]],
return false.
思路:
对array进行排序,从i =1 开始判断start是否在前一个end之前。
intervals.sort(key = lambda i :i.start)
for i in range(1,len(intervals)):
if intervals[i].start>intervals.end:
return False
return True
(36)253 Meeting Rooms II
给定由开始和结束时间[[s1,e1],[s2,e2],…](si <ei)组成的会议时间间隔数组,找到所需的最小会议室数。
思路:
1 第一步是按照起始时间对intervals进行排序
2 使用堆来处理,初始化堆和初始化一个list是一样的
3 扫描intervals里的所有interval,如果interval.start>=heap[0],则不需要新建一个meeting room,所以就用interval.end替换掉heap[0],用heapq.heapreplace,也就是先pop再push。
4 如果interval.start<=heap[0],则需要新建一个room,使用heapq.heappush将interval.end push进去
5 需要注意的是,当heap为空的时候,是需要先把第一个interval.end push到堆里去的,所以在第一个if的时候,要判断heap是否为空
6 这里用的是heap而不是stack,这是因为heap是priority queue,最小的元素在最顶端,而在这题中,我们heap里面放的是interval.end,interval.end越小的越提前结束,所以下一个interval需要和提前结束的对比。但stack是先进先出,就没有这个优势
Time: O(n)
Space: O(1)
def minMeetingRooms(self, intervals):
"""
:type intervals: List[Interval]
:rtype: int
"""
# sort the intervals by start time
intervals.sort(key = lambda x:x.start)
heap = []
for interval in intervals:
if heap and interval.start >= heap[0]:
#heapq 是python的标准库
heapq.heapreplace(heap,interval.end)
else:
heapq.heappush(heap,interval.end)
return len(heap)
Counter
(37)239. Sliding Window Maximum(Hard)
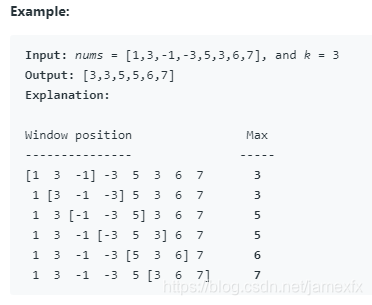
给定一个数组nums,有一个大小为k的滑动窗口,它从数组的最左边移动到最右边。您只能在窗口中看到k编号,每次滑动窗口向右移动一个位置。返回最大滑动窗口中的数字
使用线性解决
思路:
使用双端队列(存储index),队列元素降序排序,队首元素为所求的最大值。滑动窗口右滑。若出现的元素比队首大,则清空队列(使用while循环)。并将最大值插入队列中。
若比当前值小,则插入尾部。每次窗口右移的时候判断当前的最大值是否在有效范围内,不在则剔除。
#双向列表
from collections import deque
class Solution:
def maxSlidingWindow(self, nums, k):
res = []
bigger = deque()
for i, n in enumerate(nums):
# make sure the rightmost one is the smallest
while bigger and nums[bigger[-1]] <= n:
bigger.pop()
# add in
bigger += [i]
# make sure the leftmost one is in-bound
if i - bigger[0] >= k:
bigger.popleft()
# if i + 1 < k, then we are initializing the bigger array
if i + 1 >= k:
res.append(nums[bigger[0]])
return res
(38)295. Find Median from Data Stream(Hard)
中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值。所以中位数是两个中间值的平均值。
设计支持以下两个操作的数据结构:
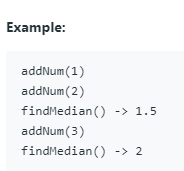
void addNum(int num) - 将数据流中的整数添加到数据结构中。
double findMedian() - 返回到目前为止所有元素的中位数。
思路:
使用二分插入元素
也还可以用一个最大堆 和一个最小堆,保持两个堆的大小平衡.让大顶堆保存小的一半的数,小顶堆保存较大的一半数O(log n) + O(1)
from heapq import *
class MedianFinder:
def __init__(self):
self.small = [] # the smaller half of the list, max heap (invert min-heap)
self.large = [] # the larger half of the list, min heap
def addNum(self, num):
if len(self.small) == len(self.large):
#heappushpop向 heap 中加入 item 元素,并返回 heap 中最小元素(之所以是负的因为要拿出来最大的元素)
heappush(self.large, -heappushpop(self.small, -num))
else:
heappush(self.small, -heappushpop(self.large, num))
def findMedian(self):
if len(self.small) == len(self.large):
return float(self.large[0] - self.small[0]) / 2.0
else:
return float(self.large[0])
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()
(39)53. Maximum Subarray(Easy)
给定整数数组nums,找到具有最大总和并返回其总和的连续子数组(包含至少一个数字)。
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
思路:
通过后一个加上前一个的和,如果前一个是正的话。
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1,len(nums)):
if nums[i-1]>0:
nums[i] +=nums[i-1]
return max(nums)
(40)325. Maximum Size Subarray Sum Equals k(Medium)
给定数组nums和目标值k,找到总和为k的子数组的最大长度。如果没有,则返回0。
Can you do it in O(n) time?
思路:
累积sum,存入字典,已有的话不更新(为保证最长),并在hashmap中找是否有另一半作差能得到k(subarray和为k)
Time Complexity: O(N) Space Complexity: O(N)
sum = 0
max_len = 0
dict = {}
dict[0] = -1 #边界情况,整个数组就是结果
for i in range(len(nums)):
sum = sum+nums[i]
if sum - k in dict:
max_len = max(max_len,i - dict.get(sum-k))
if sum not in dict:
dict[sum] = i
return max_len
(41)209. Minimum Size Subarray Sum(Medium)
给定n个正整数和正整数s的数组,找到连续子阵列的最小长度,其总和≥s。如果没有,则返回0。
思路:
1、使用左右指针
2、如果sum>=s的时候,使用while循环,左边不断的加,直到不满足条件为止
3、最后如果找不到返回0
def minSubArrayLen(self, s, nums):
"""
:type s: int
:type nums: List[int]
:rtype: int
"""
left = right = 0
min_length = len(nums)+1
sum1 = 0
for right in range(len(nums)):
sum1 +=nums[right]
#当加上一个数字后,寻找最小的长度,左边不断加,直到sum<s为止
while(sum1>=s):
min_length = min(min_length,right+1-left)
sum1 -=nums[left]
left +=1
return min_length if min_length!=len(nums)+1 else 0
(42)238. Product of Array Except Self(Medium)
给定n个整数的数组n其中n> 1,返回一个数组输出,使得output [i]等于nums [i]以外的所有nums元素的乘积
Example:
Input: [1,2,3,4]
Output: [24,12,8,6]
注意:请在没有除法的情况下解决,在O(n)中
思路:
为了只用到O(n)的时间,O(1)的空间(除结果外),采用先算除了这个数的左边,再算除了这个树的右边
def productExceptSelf(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
n = len(nums)
answer = [0]*n
#left
answer[0] = 1
for i in range(1,n):
answer[i] = nums[i-1]*answer[i-1]
#right
R = 1
for i in range(n-1,-1,-1):
answer[i] = answer[i]*R
R *= nums[i]
return answer
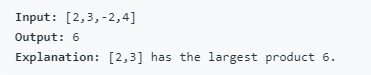
(43)152. Maximum Product Subarray(Medium)
给定整数数组nums,找到具有最大乘积的数组(包含至少一个数字)内的连续子数组。
思路:
1、两边扫各扫一次
def maxProduct(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
max1 = -2**31
#正向
product = 1
for i in range(len(nums)):
product *= nums[i]
max1 = max(max1,product)
if product==0:
product = 1
#反向
product = 1
for j in range(len(nums)-1,-1,-1):
product *= nums[j]
max1 = max(max1,product)
if product == 0:
product = 1
return max1
(44)228. Summary Ranges(Medium)
给定一个没有重复的排序整数数组,返回其范围的摘要
思路:
常规for循环,注意逗号的用法
ranges += [], 等同于 ranges += [[]]
r[1:] = n, 等同于 r[1:] = [n]
def summaryRanges(self, nums):
"""
:type nums: List[int]
:rtype: List[str]
"""
ranges = []
for n in nums:
if not ranges or n > ranges[-1][-1] + 1:
ranges += [],
ranges[-1][1:] = n,
print(ranges)
return ['->'.join(map(str, r)) for r in ranges]
(45)163. Missing Ranges(Medium)
给定一个排序的整数数组,其中元素的范围是[lower,upper]包含,返回其缺失的范围。 例如,给定[0,1,3,50,75],lower = 0和upper = 99,返回[“2”,“4-> 49”,“51-> 74”,“76-> 99” ]
思路:
1 首先判断边界条件nums is None
2 判断nums[0]是否大于low,大于,则加上区间
3 循环数组,如果nums[i]+1<nums[i+1] 则加上区间
4 判断nums[-1]是否小于upper,小于,则加上区间
ranges = []
if nums is None:
ranges +=[low,upper]
else:
if nums[0]>low:
ranges +=[low,nums[0]-1]
for i in range(len(nums)):
if nums[i]+1<nums[i+1]:
ranges +=[nums[i]+1,nums[i+1]-1]
if nums[-1]<upper:
ranges+=[nums[-1]+1,upper]
return ['->'.join(map(str,r)) if r[0]!=r[1] else str(r[0]) for r in ranges]
sort
(46)88. Merge Sorted Array(Easy)
Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.
在nums1和nums2中初始化的元素数分别为m和n。 您可以假设nums1有足够的空间(大小大于或等于m + n)来保存nums2中的其他元素。
思路:
1、用nums2来循环,当num1的值大于i时,插入
2、使用一个m变量来存储当前数组有多大
def merge(self, nums1, m, nums2, n):
"""
:type nums1: List[int]
:type m: int
:type nums2: List[int]
:type n: int
:rtype: void Do not return anything, modify nums1 in-place instead.
"""
j = 0
for i in range(n):
while j<m and nums1[j]<=nums2[i]:
j+=1
nums1.insert(j,nums2[i])
m+=1
j+=1
del nums1[m:]
(47)75. Sort Colors(Medium)
给定一个具有红色,白色或蓝色的n个对象的数组,对它们进行就地排序,使相同颜色的对象相邻,颜色顺序为红色,白色和蓝色。
def sortColors(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
# 使用快排. [0,i) [i, j) [j, k) are 0s, 1s and 2s
i =0
j=0
for k in range(len(nums)):
l = nums[k]
nums[k] =2
if l<2:
nums[j] = 1
j +=1
if l ==0:
nums[i] = 0
i +=1
(48)283. Move Zeroes(Easy)
给定一个数组nums,写一个函数将所有0移动到它的末尾,同时保持非零元素的相对顺序。
Example:
Input: [0,1,0,3,12]
Output: [1,3,12,0,0]
思路:
1、使用zero变量记录第一个0,然后使用for循环,当i不是0的时候,和zero互换,然后zero+1
# in-place
def moveZeroes(self, nums):
zero = 0 # records the position of "0"
for i in xrange(len(nums)):
if nums[i] != 0:
nums[i], nums[zero] = nums[zero], nums[i]
zero += 1
(49)376. Wiggle Subsequence(Medium)
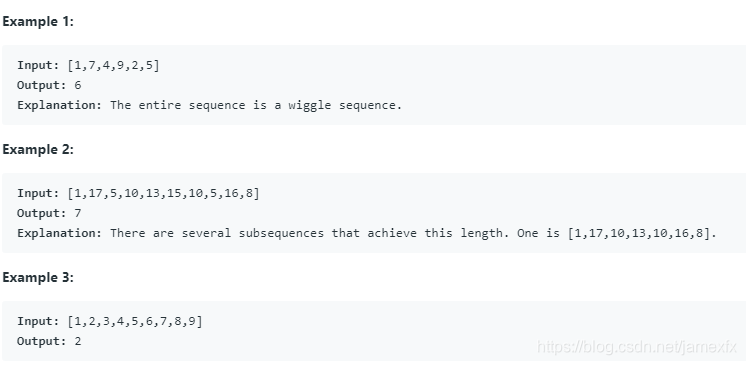
如果连续数字之间的差异在正数和负数之间严格交替,则数字序列称为摆动序列。第一个差异(如果存在)可以是正面的也可以是负面的。具有少于两个元素的序列通常是摆动序列。
例如,[1,7,4,9,2,5]是一个摆动序列,因为差异(6,-3,5,-7,3)交替为正和负. 相比之下,[1,4,7,2,5]和[1,7,4,5,5]不是摆动序列,第一个因为它的前两个差异是正的而第二个是因为它的最后差异是零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。通过从原始序列中删除一些元素(最终也为零)来获得子序列,其余元素保持原始顺序。
Can you do it in O(n) time?
思路:
由于要寻找摆动序列,寻找最长序列,其实就是寻找拐点,因为当出现连续正或者负的时候,其实是递增和递减的过程,前面的元素对结果没有影响。需要注意的是相等的连续元素,在拐点判断中这些元素可以视为一个元素,遇到相等的连续元素跳过即可。
def wiggleMaxLength(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
#边缘情况
if len(nums)<2:
return len(nums)
#建立不同数组之间的差异
diff = []
ans = 1
for i in range(1,len(nums)):
x = nums[i] - nums[i-1]
if x!=0:
diff.append(x)
if not diff:
return 1
for i in range(1,len(diff)):
if diff[i]*diff[i-1]<0:
ans +=1
return ans +1
(50)280 Wiggle Sort(Medium)
Given an unsorted array nums, reorder it in-place such that nums[0] <= nums[1] >= nums[2] <= nums[3]…
For example, given nums = [3, 5, 2, 1, 6, 4], one possible answer is [1, 6, 2, 5, 3, 4].
就是给定一个数组,排序这个数组,使得奇数位大于左边和右边,偶数位小于左边和右边
思路:
可以分为偶数和奇数位进行讨论,不满足情况可以直接交换两个数字
def swapsort(self,nums):
if len(nums)<2:
return
for i in range(len(nums)-1):
if i%2 ==0:
if nums[i]>nums[i+1]:
nums[i],nums[i+1] = nums[i+1],nums[i]
else:
if nums[i]<nums[i+1]:
nums[i],nums[i+1] = nums[i+1],nums[i]
(51)324. Wiggle Sort II(Medium)
给定一个未排序的数组nums,重新排序,使得nums [0] <nums [1]> nums [2] <nums [3] …
Example 1:
Input: nums = [1, 5, 1, 1, 6, 4]
Output: One possible answer is [1, 4, 1, 5, 1, 6]
思路:
方法一: O(nlogn)时间排序+O(n)空间辅助数组解法
给数组进行排序,然后将前面的数插入奇数组中,后面的数插入偶数组中O(nlogn)O(n)
. arr = sorted(nums)
for i in range(1, len(nums), 2): nums[i] = arr.pop()
for i in range(0, len(nums), 2): nums[i] = arr.pop()
方法二: O(n)时间复杂度+O(1)空间复杂度解法:(递归+快排切分法 和 非递归+快排切分法)
这个方法是比较重要的,在求第K小的元素的时候,求中位数的时候都是可以用到的。
启发来源与快速排序的切分法,比如我们需要找到数组第K小的元素,首先将数组a[low,high]切分返回j,使得a[low,j-1]都小于等于j,而a[j+1,high]都大于等于a[j]。如果j==k,那么j位置的元素就是我们要找到的第K小的元素。如果j>k,就要切分左子数组。如果j<k就要切分右子数组。不断地缩小选定的子数组的规模直到剩下一个元素,则它就是最终我们需要找的第k小的元素。
经过数学推导,这种快速切分法寻找中位数仅仅位线性量级。是寻找中位数最为快速的方法。
有递归和非递归两种方式(即递归+快排切分法 和 非递归+快排切分法)
求中值:
Pos = (len(nums)+1)//2
求最小K值:
Pos = k
求最大K值
Pos = len(nums)+2-k
class Solution(object):
def wiggleSort(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
#递归方案
self.recursive(nums,0,len(nums)-1,(len(nums)+1)//2)
#非递归方案
#self.non_recursive(nums,0,len(nums)-1,(len(nums)+1)//2)
middle = (len(nums)+1)//2
nums[::2],nums[1::2] = nums[:middle][::-1],nums[middle:][::-1]
# 切分法接口(选定一个数,然后把大于这个数放左边,小于这个数放右边,i代表小于这个数的最大index,j代表大于这个数的最小index)
def partition(self,nums,start,end):
mid = (start+end)//2
pivot = nums[mid]
i = start -1
j = end + 1
k = start
while k<j:
if nums[k]<pivot:
i+=1
nums[i],nums[k] = nums[k],nums[i]
elif nums[k]>pivot:
j-=1
nums[j],nums[k] = nums[k],nums[j]
k-=1
k+=1
return i,j
def recursive(self,nums,start,end,pos):
i,j = self.partition(nums,start,end)
#i + 1-start 代表左边的元素共有多少个,如果左边的元素个数大于pos,那么中位数在左边,+1是因为index
if i + 1 -start >= pos:
return self.recursive(nums,start,i,pos)
#左边元素小于pos,j-start代表j距离start的个数,如果大于pos,说明既不满足左边元素太多,右边元素太
#多,所以就是中值
elif j-start>=pos:
return nums[j-1]
#左边元素小于pos,右边元素大于pos,中位数在右边
else:
return self.recursive(nums,j,end,pos-(j-start))
def non_recursive(self,nums,start,end,pos):
while True:
i,j = self.partition(nums,start,end)
#i + 1-start 代表左边的元素共有多少个,如果左边的元素个数大于pos,那么中位数在左边,+1是因为index
if i + 1 -start >= pos:
end = i
#左边元素小于pos,j-start代表j距离start的个数,如果大于pos,说明既不满足左边元素太多,右边元素太
#多,所以就是中值
elif j-start>=pos:
return nums[j-1]
#左边元素小于pos,右边元素大于pos,中位数在右边
else:
pos -= (j-start)
start = j
String
(52)28. Implement strStr() (Easy)
返回haystack中第一次出现针的索引,如果针不是haystack的一部分,则返回-1。
思路:
思路一:
使用循环
def strStr(self, haystack, needle):
"""
:type haystack: str
:type needle: str
:rtype: int
"""
for i in range(len(haystack) - len(needle)+1):
if haystack[i:i+len(needle)] == needle:
return i
return -1
思路二:
经典的KMP算法 时间复杂度O(m+n)
假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置
- 如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
- 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。
- next 代表当前字符串之前有多大长度的相同前缀后缀,next就是找最大对称长度的前缀后缀,然后整体右移一位,初值赋为-1
已知next [0, …, j],如何求出next [j + 1]
- 若p[k] == p[j],则next[j + 1 ] = next [j] + 1 = k + 1;
- 若p[k ] ≠ p[j],如果此时p[ next[k] ] == p[j ],则next[ j + 1 ] = next[k] + 1,否则继续递归前缀索引k = next[k],而后重复此过程。
- (此过程可以看july写的例子)
改进next
- 当p[j] != s[i] 时,下次匹配必然是p[ next [j]] 跟s[i]匹配,如果p[j] = p[ next[j] ],必然导致后一步匹配失败(因为p[j]已经跟s[i]失配,然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配,很显然,必然失配),所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ]咋办呢?如果出现了,则需要再次递归,即令next[j] = next[ next[j] ]。
寻找next的代码
def find_next(self,patten):
next = [0]*len(patten)
next[0] = -1
j = 0
k = -1
while j<len(patten) - 1:
# p[k]表示前缀,p[j]表示后缀
#如果前缀和后缀的字符相同,则next[j] = k
if (k ==-1 or patten[j] == patten[k]):
j+=1
k+=1
#为了防止patten[j+1] == patten[k+1],这样会重复验证,必定失败
if patten[j]!=patten[k]:
next[j] = k #未改进之前只需要这一步
else:
next[j] = next[k]
else:
k = next[k]
return next
查找P在S中的位置
def strStr(self, haystack, needle):
"""
:type haystack: str
:type needle: str
:rtype: int
"""
# 考虑边界问题
if len(needle)==0:
return 0
#计算next数组
next = self.find_next(needle)
i = 0
j = 0
while(i<len(haystack) and j<len(needle)):
#如果j=-1 或者当前字符匹配成功(s[i] == p[j]),则i++,j++
if (j ==-1 or haystack[i] == needle[j]):
i +=1
j +=1
#如果匹配失败,则令i不变,j = next[j]
else:
j = next[j]
if j == len(needle):
return i-j
else:
return -1
还有BM算法和Sunday算法,是比KMP算法更快的算法
(53)14. Longest Common Prefix(Easy)
编写一个函数来查找字符串数组中最长的公共前缀字符串。 如果没有公共前缀,则返回空字符串“”。
思路:学会使用zip函数
def longestCommonPrefix(self, strs):
"""
:type strs: List[str]
:rtype: str
"""
prefix = ""
for i in zip(*strs):
if i.count(i[0])==len(i):
prefix +=i[0]
else:
return prefix
return prefix
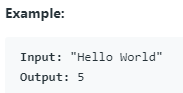
(54)58. Length of Last Word(Easy)
给定字符串s由大写/小写字母和空格字符’‘组成,返回字符串中最后一个单词的长度。
rstrip(’ ') 是指去除末尾的空格
s = s.rstrip(' ').split(' ')
if len(s) ==0:
return 0
else:
return len(s[-1])
(55)387. First Unique Character in a String(Easy)
给定一个字符串,找到它中的第一个非重复字符并返回它的索引。如果它不存在,则返回-1。
Examples:
s = “leetcode”
return 0.
s = “loveleetcode”,
return 2.
思路:
使用字典存储,然后使用s循环,找出字典中为1的
def firstUniqChar(self, s):
"""
:type s: str
:rtype: int
"""
dict = {}
for i in s:
if i not in dict:
dict[i] =1
else:
dict[i]+=1
for i,c in enumerate(s):
if dict[c] ==1:
return i
return -1
# return min([s.index(char) for char in set(s) if s.count(char) == 1] or [-1])
(56)383. Ransom Note
给定一个任意赎金票据字符串和另一个包含所有杂志字母的字符串,写一个函数,如果赎金票据可以从杂志上构建,它将返回true;否则,它将返回false。
杂志字符串中的每个字母只能在赎金票据中使用一次
def canConstruct(self, ransomNote, magazine):
"""
:type ransomNote: str
:type magazine: str
:rtype: bool
"""
for i in set(ransomNote):
if magazine.count(i)< ransomNote.count(i):
return False
return True
(57)344. Reverse String
编写一个反转字符串的函数。输入字符串以char []字符数组的形式给出。 不要为另一个数组分配额外的空间,必须通过使用O(1)额外内存修改输入数组来实现此目的
You may assume all the characters consist of printable ascii characters.
思路:
分一半
def reverseString(self, s):
"""
:type s: List[str]
:rtype: None Do not return anything, modify s in-place instead.
"""
n = len(s)
for i in range(n//2):
s[i],s[n-i-1] = s[n-i-1],s[i]
(58)151. Reverse Words in a String(Medium)
给定输入字符串,逐字反转字符串。
思路:
方法一:
使用python 的split函数
def reverseWords(self, s):
"""
:type s: str
:rtype: str
"""
l = [i for i in s.split() if i!=''][::-1]
return ' '.join(l)
方法二:(为了不使用[::-1],split())
主要是最前面要判断一下是空格结尾还是非空格结尾
def reverseWords(self, s):
word = ""
words = ""
for i in range(len(s)-1,-1,-1):
if s[i] ==' ' and word!='':
words += (word+' ')
word = ''
elif s[i]!=' ':
word = s[i]+word
if word == '' and len(words)>0 and words[-1]==' ':
return words[:-1]
else:
return words+word
(59)186. Reverse Words in a String II(Medium)
给定输入字符串,逐字反转字符串。一个单词被定义为一系列非空格字符。 输入字符串不包含前导或尾随空格,并且单词始终由单个空格分隔。
你可以在没有分配额外空间的情况下就地进行吗?
For example,
Given s = “the sky is blue”,
return “blue is sky the”.
思路:
由于不存在前面后面的空格,所以无需考虑
可以先反转整个数组,然后再翻转每个单词,写一个翻转接口,就不需要用到空间了
class Solution:
def reverseWords(self,s):
def reverse(s, start, end):
while start < end:
s[start], s[end] = s[end], s[start]
start += 1
end -= 1
if len(s)==0:
return s
s = list(s)
reverse(s,0,len(s)-1)
start = 0
end = 0
while start<len(s):
end = start
while end < len(s)-1 and s[end+1]!=' ':
end +=1
reverse(s,start,end)
start = end + 2
return s
y = Solution()
s = "the sky is blue"
s = y.reverseWords(s)
print(''.join(s))
(60)345. Reverse Vowels of a String(Easy)
编写一个函数,该函数将字符串作为输入,并仅反转字符串的元音
Example 2:
Input: “leetcode”
Output: “leotcede”
思路:
所有string类型都要转换为list
1、给定两个指针,分别前后判别是否由元音
def reverseVowels(self, s: 'str') -> 'str':
vowels = {'a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'}
L = list(s)
i = 0
j = len(L)-1
while i<j:
while i<j and L[i] not in vowels:
i +=1
while j>i and L[j] not in vowels:
j -=1
L[i],L[j] = L[j],L[i]
i +=1
j -=1
return ''.join(L)
(61)205. Isomorphic Strings(Easy)
给定两个字符串s和t,确定它们是否是同构的
如果s中的字符可以替换为t,则两个字符串是同构的
在保留字符顺序的同时,必须用另一个字符替换所有出现的字符。没有两个字符可以映射到相同的字符,但字符可以映射到自身
思路:
1、设立两个字典分别对应两个字符串的映射(正向、反向)
def isIsomorphic(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
d1,d2 = {},{}
for w1,w2 in zip(s,t):
if ((w1 in d1) and d1[w1]!=w2) or ((w2 in d2) and d2[w2]!=w1):
return False
else:
d1[w1] = w2
d2[w2] = w1
return True
(62)293. Flip Game(Easy)
You are playing the following Flip Game with your friend: Given a string that contains only these two characters: + and -, you and your friend take turns to flip two consecutive “++” into “–”. The game ends when a person can no longer make a move and therefore the other person will be the winner.Write a function to compute all possible states of the string after one valid move.
思路:
就是把所有反转一次的可能写出来
def generatePossibleNextMoves(self,s):
res = []
if s:
for i in range(1,len(s)):
if s[i-1:i+1] =='++':
res.append(s[:i-1]+'--'+s[i+1:])
return res
(63)294.Flip Game II(Medium)
You are playing the following Flip Game with your friend: Given a string that contains only these two characters: + and -, you and your friend take turns to flip two consecutive “++” into “–”. The game ends when a person can no longer make a move and therefore the other person will be the winner.
Write a function to determine if the starting player can guarantee a win.
input: a string with only + and - two kinds of characters
output: for a given input, based on the game rule, return whether there is one strategy that can make the first player win, if yes, return true, if there is none, return false
corner: when the string if null, return false
思路:
交替True,如果一个人是True,另一个人就是False
使用递归搞定
def canWin(self,s):
for i in range(1,len(s)):
if s[i-1:i+1] =='++':
if (!canWin(s[:i-1]+'--'+s[i+1:])):
return True
return False
(64)290. Word Pattern(Easy)
Given a pattern and a string str, find if str follows the same pattern.
Here follow means a full match, such that there is a bijection between a letter in pattern and a non-empty word in str.
思路:
寻找str和patten相同的格式的
使用字典,记得判断边界(两个数组长度是否一样)
def wordPattern(self, pattern: 'str', str: 'str') -> 'bool':
str = str.split()
dict1 = {}
if len(str)!=len(pattern):
return False
for i,v in enumerate(pattern):
if v not in dict1:
if str[i] in dict1.values():
return False
dict1[v] = str[i]
elif dict1[v]!=str[i]:
return False
return True
(65)242. Valid Anagram(Easy)
Given two strings s and t , write a function to determine if t is an anagram of s.
您可以假设该字符串仅包含小写字母。
如果输入包含unicode字符怎么办?您如何使您的解决方案适应这种情况?
思路:
用字典,怎么用get,看代码
def isAnagram(self, s: 'str', t: 'str') -> 'bool':
map_s = {}
map_t = {}
for i in s:
map_s[i] = map_s.get(i,0)+1
for i in t:
map_t[i] = map_t.get(i,0)+1
return map_s == map_t
(66)49. Group Anagrams(Medium)
给定一个字符串数组,将字谜组合在一起。
Input: [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”],
Output:[[“ate”,“eat”,“tea”],[“nat”,“tan”],[“bat”]]
思路:
1.将字符排序,然后存到字典里O(NKlogK) (因为涉及排序)
2.算字符的个数,然后存到字典 O(NK)
字典a.values()
def groupAnagrams(self, strs):
"""
:type strs: List[str]
:rtype: List[List[str]]
"""
a = collections.defaultdict(list)
for s in strs:
count = [0]*26
for c in s:
count[ord(c)-ord('a')] +=1
a[tuple(count)].append(s)
return a.values()
(67)249. Group Shifted Strings(Medium)
给定一个字符串,我们可以将其每个字母“移位”到其后续字母,例如:“abc” - >“bcd”。我们可以保持“转移”形成序列:“abc” -> “bcd” -> … -> “xyz”
给定仅包含小写字母的字符串列表,将属于相同移位序列的所有字符串分组。
Input: [“abc”, “bcd”, “acef”, “xyz”, “az”, “ba”, “a”, “z”],
Output:
[
[“abc”,“bcd”,“xyz”],
[“az”,“ba”],
[“acef”],
[“a”,“z”]
]
思路:
1、首先要定义一个key函数,abc的key就是(‘a’ - ‘b’), (‘b’ - ‘c’)
2、然后需要对每一行的结果进行排序
(68) 87. Scramble String(Hard)
判断一个字符串是否为另一个字符串“乱序”得到,使用树结构,通过叶子对调的形式
思路:使用dfs,自然要循环所有从i位置切断的树。
一步步缩小,(左边和左边相同,右边和右边相同) 或者(左边和右边相同,右边和左边相同)
s[:i]==s[-i:] and s[i:]==s[:-i]
def isScramble(self, s1, s2):
"""
:type s1: str
:type s2: str
:rtype: bool
"""
if len(s1)!=len(s2) or sorted(s1)!=sorted(s2):
return False
if len(s1)<4 or s1==s2:
return True
for i in range(1,len(s1)):
if (self.isScramble(s1[:i],s2[:i]) and self.isScramble(s1[i:],s2[i:])) or (self.isScramble(s1[:i],s2[-i:]) and self.isScramble(s1[i:],s2[:-i])):
return True
return False
(69)179. Largest Number(Medium)
Given a list of non negative integers, arrange them such that they form the largest number.
思路:
1、自己定义一个比较函数(因为需要返回倒序,当a大于b,返回负数),然后用sorted()函数
2、把后面的0给去除掉,lstrip(‘0’) 同时要注意数组元素都为0的情况
def largestNumber(self, nums):
"""
:type nums: List[int]
:rtype: str
"""
def compare(a,b):
return int(b+a) - int(a+b)
nums = sorted([str(i) for i in nums],cmp = compare)
return ''.join(nums).lstrip('0') or '0'
(70)6. ZigZag Conversion (Medium)
The string “PAYPALISHIRING” is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
And then read line by line: “PAHNAPLSIIGYIR”
思路:
1、记得判断是上升还是下降
def convert(self, s, numRows):
"""
:type s: str
:type numRows: int
:rtype: str
"""
if numRows ==1 or len(s)<=numRows:
return s
step =1
index = 0
L = [""]*numRows
for i in s:
L[index] +=i
if index ==0:
step = 1
elif index==numRows-1:
step = -1
index +=step
return ''.join(L)
(71)161. One Edit Distance
给定两个字符串s和t,确定它们是否相隔一个编辑距离。(增,删,替换)
思路:
1、首先判断两个长度的差绝对值是不是小于1
2、分三种情况进行讨论s>t、s==t、s<t
def isOneEditDistance(self,s,t):
len_s,len_t = len(s),len(t)
if abs(len_s-len_t)>1:
return False
s,t = list(s),list(t)
if len_s<len_t:
for i ,c in enumerate(s):
if s[i]!=t[i]:
s.insert(i,t[i])
return s==t
return True
elif len_s == len_t:
for i ,c in enumerate(s):
if s[i] !=t[i]:
s[i] = t[i]
return s==t
return True
else:
for i ,c in enumerate(t):
if s[i]!=t[i]:
t.insert(i,s[i])
return s==t
return True
(72)38. Count and Say(Easy)
The count-and-say sequence is the sequence of integers with the first five terms as following:
1
11
21
1211
111221
1 is read off as “one 1” or 11.
11 is read off as “two 1s” or 21.
21 is read off as “one 2, then one 1” or 1211.
Given an integer n where 1 ≤ n ≤ 30, generate the nth term of the count-and-say sequence.
def countStr(self,s):
count = 0;ans = "";tmp = s[0]
for i in range(len(s)):
if s[i] == tmp:
count += 1
else:
ans += str(count) + tmp
tmp = s[i];count = 1
ans += str(count) + tmp
return ans
def countAndSay(self, n):
"""
:type n: int
:rtype: str
"""
ans = '1'
while n > 1:
ans = self.countStr(ans)
n -= 1
return ans
(73)358 Rearrange String k Distance Apart(Hard)
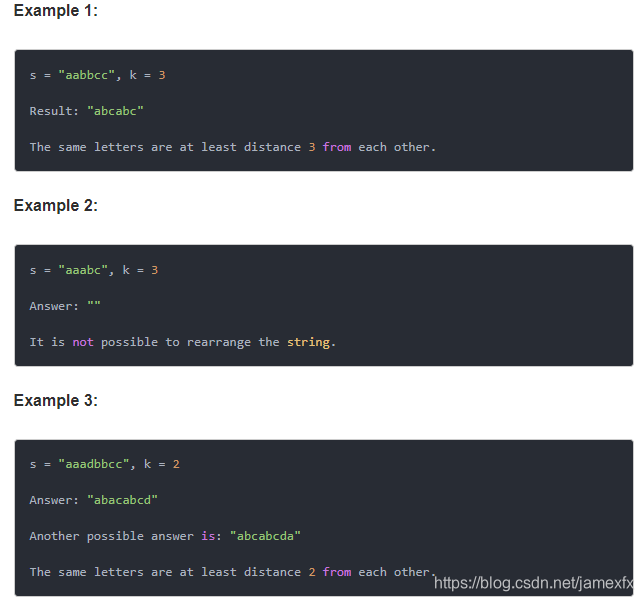
给定非空字符串s和整数k,重新排列字符串,使得相同的字符至少彼此距离为k。
所有输入字符串都以小写字母给出。如果无法重新排列字符串,则返回空字符串“”。
思路:
1、使用counter统计每个字符出现的次数,然后使用最小堆函数(使用-val来实现最大堆),每次弹出出现次数最多的字符
2、如果剩余的字符个数不够K,那么不满足,return ‘’
3、每次弹出之后不能直接放入堆中,先放入一个临时数组,单次操作完毕后再插入堆中
时间复杂度是O(N),空间复杂度是O(N)
#类似于字典的存储方式
words_count = collections.Counter(words)
#创建堆
que = []
heapq.heapify(que)
#把元素加入堆中
for w,v in words_count.items():
heapq.heappush(que,(-v,w))
import collections
import heapq
def rearrangeString(words,k):
n = len(words)
words_count = collections.Counter(words)
que = []
heapq.heapify(que)
for w,v in words_count.items():
heapq.heappush(que,(-v,w))
res = ''
while que:
cnt = min(n,k)
used = []
for i in range(cnt):
if not que:
return ''
v,w = heapq.heappop(que)
res +=w
if v+1!=0:
used.append((v+1,w))
n -=1
for use in used:
heapq.heappush(que,use)
return res
(74)316. Remove Duplicate Letters(Hard)
给定一个只包含小写字母的字符串,删除重复的字母,这样每个字母只出现一次。您必须确保在所有可能的结果中,您的结果在字典顺序中是最小的。
思路:
1、先把每个字符最大的index给找出来
2、然后循环判断,如果不在result中,则加入,如果加入的元素字符较小,并且index也较最后一个元素小,就删除最后一个元素
def removeDuplicateLetters(self, s):
"""
:type s: str
:rtype: str
"""
# 相当于把每个字符最大的index存储起来
rindex = {c: i for i, c in enumerate(s)}
print(rindex)
result = ''
#循环判断,如果不在result中,则加入,如果加入的元素字符较小,并且index也较小,就删除最后一个元素
for i, c in enumerate(s):
if c not in result:
print(c,result[-1:],result)# [-1:] -1后面不加:会溢出
while c < result[-1:] and i < rindex[result[-1]]:
result = result[:-1]
result += c
return result
(75)271 Encode and Decode Strings(Medium)(未写)
(76)168. Excel Sheet Column Title(Easy)
给定正整数,返回Excel工作表中显示的相应列标题
1 -> A
2 -> B
3 -> C
…
26 -> Z
27 -> AA
28 -> AB
def convertToTitle(self, n):
"""
:type n: int
:rtype: str
"""
r = ''
while(n>0):
n -=1
r = chr(n%26+65)+r
n /=26
return r
(77)171. Excel Sheet Column Number(Easy)
给定Excel工作表中显示的列标题,返回其相应的列号。
A -> 1
B -> 2
C -> 3
…
Z -> 26
AA -> 27
AB -> 28
…
def titleToNumber(self, s):
"""
:type s: str
:rtype: int
"""
s = s[::-1]
sum_s = 0
for exp,char in enumerate(s):
sum_s +=(ord(char)-65+1)*(26**exp)
return sum_s
(78)12. Integer to Roman(Medium)
数字转罗马
def intToRoman(self, num):
"""
:type num: int
:rtype: str
"""
#1~9
I = ['','I','II','III','IV','V','VI','VII','VIII','IX']
#10-90
X = ['','X','XX','XXX','XL','L','LX','LXX','LXXX','XC']
#100-900
C = ['','C','CC','CCC','CD','D','DC','DCC','DCCC','CM']
#1000-3000
M = ['','M','MM','MMM']
return M[num/1000]+C[(num%1000)/100]+X[(num%100)/10]+I[(num%10)]
(79)13. Roman to Integer(Easy)
罗马到数字
思路:
1、先统计出每个罗马数字的个数
2、然后减去前面放置的个数
def romanToInt(self, s):
"""
:type s: str
:rtype: int
"""
r = 0
num_I = s.count('I')
num_V = s.count('V')
num_X = s.count('X')
num_L = s.count('L')
num_C = s.count('C')
num_D = s.count('D')
num_M = s.count('M')
r +=num_I*1
r +=num_V*5
r +=num_X*10
r +=num_L*50
r +=num_C*100
r +=num_D*500
r +=num_M*1000
if num_I>0:
r += (s.count('IV')+s.count('IX'))*(-2)
if num_X>0:
r += (s.count('XL')+s.count('XC'))*(-20)
if num_C>0:
r += (s.count('CD')+s.count('CM'))*(-200)
return r
(80)273. Integer to English Words(Hard)
将非负整数转换为其英语单词表示。鉴于输入保证小于231 - 1。
Input: 1234567891
Output: “One Billion Two Hundred Thirty Four Million Five Hundred Sixty Seven Thousand Eight Hundred Ninety One”
思路:
1、定义小于20,十位数,千位数的字符
2、循环判断,每次除以1000,用于千位数
3、然后定义一个helper
def __init__(self):
self.lessThan20 = ["","One","Two","Three","Four","Five","Six","Seven","Eight","Nine","Ten","Eleven","Twelve","Thirteen","Fourteen","Fifteen","Sixteen","Seventeen","Eighteen","Nineteen"]
self.tens = ["","Ten","Twenty","Thirty","Forty","Fifty","Sixty","Seventy","Eighty","Ninety"]
self.thousands = ["","Thousand","Million","Billion"]
def numberToWords(self, num):
if num == 0:
return "Zero"
res = ""
for i in range(len(self.thousands)):
if num % 1000 != 0:
res = self.helper(num%1000) + self.thousands[i] + " " + res
num /= 1000
return res.strip()
def helper(self, num):
if num == 0:
return ""
elif num < 20:
return self.lessThan20[num] + " "
elif num < 100:
return self.tens[num/10] + " " + self.helper(num%10)
else:
return self.lessThan20[num/100] + " Hundred " + self.helper(num%100)
(81)246. Strobogrammatic Number(Easy)
频闪编号是旋转180度时看起来相同的数字(看着倒置)。 写一个函数来确定一个数字是否是strobogrammatic。数字表示为字符串。
思路:
1、建立字典
2、然后倒置,判断是否相同
d = {'0':'0','1':'1','6':'9','8':'8','9':'6'}
ans = ''
for n in num:
if n not in d:
return False
ans +=d[n]
return ans[::-1] ==num
(82)247. Strobogrammatic Number II(Medium)
频闪编号是旋转180度时看起来相同的数字(看着倒置)。 找到所有长度为n的频闪编号。
Given n = 2, return [“11”,“69”,“88”,“96”].
思路:
可以像是一层层的给字符串从里向外穿衣服一样DFS生成所有的解.
其中翻转之后和自身相等有0, 1, 8, 在n为奇数的情况下最里面的一个数可以为这三个数的任意一个. 再外边就一次给两端添加一个对称的字符. 如果是最外层的话需要注意不能是为0.
def __init__(self):
result =[]
odd = [‘0’,'1','8']
even = ['00','11','69','88','96']
def findStrobogrammatic(n):
if n==0:
return ['']
if n==1:
return self.find(1)
return [l for l in self.find(n) if l[0]!='0' and n>1]
def find(self,n):
if n==1:
return odd
if n==2:
return even
mid = self.find(n-2)
res = [s[0]+m+s[1] for s in even for m in mid]
return res
(83)248 Strobogrammatic Number III(Hard)
给定一个范围,求这个范围内的频闪编号
思路:和上一题差不多,只不过多了判断在不在范围内
(84)68. Text Justification(Hard)
给定一个单词数组和一个宽度maxWidth,格式化文本,使每行具有正确的maxWidth字符,并且完全(左和右)对齐。
#分为两种情况,末行和非末行
#末行,所有单词中间只有一个空格,后面全部补空格
#非末行,只有一个单词,靠左放,其它补空格,
#多个单词,计算几个num和几个多余的空格前
#每个间隔再多方extra/num个,前extra%num个间隔再多放个空格。
n = len(words)
i = 0
res = []
while(i<n):
j = i+1
len_words = len(words[i])
while j<n and len_words+1+len(words[j])<=maxWidth:
len_words +=1+len(words[j])
j +=1
line = words[i]
if j==n:
for k in range(i+1,n):
line +=' ' +words[k]
while(len(line)<maxWidth):
line +=' '
else:
nums = j-i-1
if j == i+1:
while(len(line)<maxWidth):
line += ' '
else:
extraspace = maxWidth -len_words
for k in range(i+1,j):
line += ' '
for l in range((extraspace/nums)):
line +=' '
if (k-i<=extraspace%nums):
line +=' '
line +=words[k]
res.append(line)
i =j
for k in res:
print(len(k))
return res
(85)65.Valid Number(Hard)
判断是不是合法的数字
使用状态机来做(num,dot,exp)分别用来表示前面有没有数字,点,科学记数法e
def isNumber(self, s):
"""
:type s: str
:rtype: bool
"""
#可以使用状态机来做 https://blog.csdn.net/weixin_38314447/article/details/79075851
begin, last = 0,len(s)-1
#将字符串前后的空格去掉
while begin<=last and s[begin] == ' ':
begin +=1
while begin<=last and s[last] == " ":
last -=1
#数字前为正号或者负号的情况,首位后移
if begin< last and (s[begin]=='+' or s[begin] == '-'):
begin +=1
num,dot,exp =False,False,False
while begin<=last:
# 该字符为数字
if s[begin]>='0' and s[begin]<='9':
num = True
#若首位为'.'则返回False, 否则标记为小数
elif s[begin]=='.':
if dot or exp:
return False
dot = True
#若首位为'e',则返回False,否则记作科学计数
elif s[begin] =='e' or s[begin] == 'E':
if exp or not num:
return False
exp,num = True,False#后面必须要有数字才行
#若遇到正负号,则判断前一位是否为‘e'
elif s[begin]=='+' or s[begin]=='-':
if s[begin-1] !='e':
return False
else:
return False
begin +=1
return num
Sliding Window
(86)76. Minimum Window Substring(Hard)
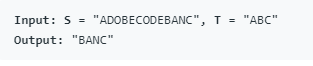
给定一个字符串S和一个字符串T,找到S中的最小窗口,它将包含复杂度为O(n)的T中的所有字符。
- 先统计t中字符串的数量
- 定义left、right、min_len指针,left用来收缩,right用来扩张,min_len用来存储最小字符串的位置
- 定义set(len_t),当
dict[s[right]]==0时,set(len_t)-=1
def minWindow(self, s, t):
"""
:type s: str
:type t: str
:rtype: str
"""
len_s = len(s)
len_t = len(t)
if len_t>len_s or len_s==0 or len_t ==0:
return ''
countT1 = {}
for i in t:
if i in countT1:
countT1[i] +=1
else:
countT1[i] =1
left =0
min_len = (0,100000)
len_t = len(set(t))
for right in range(len(s)):
if s[right] in countT1:
countT1[s[right]] -=1
if countT1[s[right]] ==0:
len_t -=1
if len_t ==0:
while True:
if s[left] not in countT1:
left+=1
else:
#如果最左边是t的值的话,则值加一,然后左移一位,退出循环继续找
countT1[s[left]] +=1
##很有可能出现某个单词次数小于0的情况,直到其中一个大于0时,统计
if countT1[s[left]]>0:
len_t +=1
if (min_len[1]-min_len[0])>right -left:
min_len = (left,right)
left +=1
break
left +=1
if min_len[1]==100000:
return ''
return s[min_len[0]:min_len[1]+1]
(87)30. Substring with Concatenation of All Words(Hard)
您将获得一个字符串s , 以及一个长度相同的单词words。在s中查找substring(s)的所有起始索引,它们是单词中每个单词的串联,只有一次,没有任何插入字符。(单词可以不按顺序)
Input:
s = “barfoothefoobarman”,
words = [“foo”,“bar”]
Output: [0,9]
Explanation: Substrings starting at index 0 and 9 are “barfoor” and “foobar” respectively.
The output order does not matter, returning [9,0] is fine too.
思路:
1、先将words存入字典,统计每个单词的个数
2、for循环,while寻找
3、还需要一个字典存储已经有的词
def findSubstring(self, s, words):
"""
:type s: str
:type words: List[str]
:rtype: List[int]
"""
numword = len(words)
if numword ==0 or len(s)==0:
return []
dict ={}
for i in words:
if i not in dict:
dict[i] =1
else:
dict[i] +=1
j = 0
lw = len(words[0])
res =[]
for i in range(len(s)-lw*numword+1):
count_word ={}
j=0
while (j<numword):
temp = s[i+j*lw:i+(j+1)*lw]
if temp not in dict:
break
if temp not in count_word:
count_word[temp] = 1
else:
count_word[temp] +=1
if count_word[temp]>dict[temp]:
break
j+=1
if j == numword:
res.append(i)
return res
(88)3.Longest Substring Without Repeating Characters(Medium)
给定一个字符串,找出其没有重复字符的最大子序列的长度。
思路:定义max_len、start、substring
循环s,当s[end]不在substring->substring+s[end]
否则:while s[start]!=s[end]: start++
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
max_len = 0
start = 0
substring = ''
for end in range(len(s)):
if s[end] in substring:
max_len = max(max_len,len(substring))
while s[start] !=s[end]:
start +=1
start +=1
substring = s[start:end+1]
else:
substring +=s[end]
return max(max_len,len(substring))
(89)340. Longest Substring with At Most K Distinct Characters(Hard)
给定一个字符串,找到包含最多k个不同字符的最长子字符串T的长度。
Example 1:
Input: s = “eceba”, k = 2
Output: 3
Explanation: T is “ece” which its length is 3.
Example 2:
Input: s = “aa”, k = 1
Output: 2
Explanation: T is “aa” which its length is 2.
思路:
使用滑动窗口,然后使用字典进行存储
def lengthOfLongestSubstringKDistinct(self,s,k):
if k==0:
return 0
result = 0
dict = {}
left = 0
for right in range(len(s)):
if s[right] not in dict:
dict[s[right]] = 1
else:
dict[s[right]] +=1
while(len(dict)>k):
if dict[s[left]] ==1:
dict.pop(s[left])
else:
dict[s[left]] -=1
left +=1
result = max(result,right-left+1)
return result
(90)395. Longest Substring with At Least K Repeating Characters(Medium)
查找给定字符串的最长子字符串T的长度(仅由小写字母组成),以便T中的每个字符显示不少于k次。
思路:
如果s中某个字符的数量小于k,那么这个字符一定不能在字串中。
所以使用递归
def longestSubstring(self, s, k):
"""
:type s: str
:type k: int
:rtype: int
"""
for c in set(s):
if s.count(c)<k:
return max(self.longestSubstring(t,k) for t in s.split(c))
return len(s)
(91)159 Longest Substring with At Most Two Distinct Characters(Hard)
给定一个字符串,找到包含最多2个不同字符的最长子字符串T的长度。
思路:
就是把340题中的K = 2,其它一样
String(Palindrome)
(92)125. Valid Palindrome(Easy)
给定一个字符串,确定它是否是回文,只考虑字母数字字符并忽略大小写。 注意:出于此问题的目的,我们将空字符串定义为有效的回文
思路:
1、要使用字符串的isalnum()判断是否是字母or数字
2、要将所有字母转化为小写
def isPalindrome(self, s):
"""
:type s: str
:rtype: bool
"""
s = [i.lower() for i in s if i.isalnum()]
return s ==s[::-1]
(93)266. Palindrome Permutation(Easy)
给定一个字符串,确定字符串的排列是否可以形成回文
Input: “code”
Output: false
Example 2:
Input: “aab”
Output: true
Example 3:
Input: “carerac”
Output: true
思路:
字符串最多只有一个奇数的字母放在中间,剩下的必须都是偶数,因此定义一个变量用来判断有没有超过两个奇数的变量
def canPermutePalindrome(self, s):
"""
:type s: str
:rtype: bool
"""
count = collections.Counter(s)
c = 0
for i in count:
if count[i]%2 !=0:
c +=1
if c>1:
return False
return True
(94)5. Longest Palindromic Substring(Medium)
给定一个字符串s,找到s中最长的回文子字符串。您可以假设s的最大长度为1000。
思路:
分为两种情况1、回文串是奇数2、回文串是偶数
跳入一个函数判断当前 i 前后最大回文
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
substring = ''
for i in range(len(s)):
res = self.findsub(s,i,i)
if len(res)>len(substring):
substring = res
res = self.findsub(s,i,i+1)
if len(res)>len(substring):
substring = res
return substring
def findsub(self,s,j,k):
while j>=0 and k<len(s) and s[j] == s[k]:
j-=1
k+=1
return s[j+1:k]
(95)9. Palindrome Number(Easy)
判断该数字是不是回文
思路:(两个特点,x>=0 and (x%10!=0 or x==0))
可以用暴力破解(从左从右判断),更好的方法是截取一半
if (x<0 or (x %10 ==0 and x !=0)):
return False
revertedNumber = 0
while (x > revertedNumber):
revertedNumber = revertedNumber * 10 + x%10
x= int(x/10)
return x ==revertedNumber or x == int(revertedNumber/10)
(96)214. Shortest Palindrome(Hard)
给定一个字符串s,您可以通过在其前面添加字符将其转换为回文结构。通过执行此转换,找到并返回您可以找到的最短回文。
思路:
先搞清楚KMP算法
1、借助KMP的算法,查看最长的公共长度(第一个值仍然为0,并且我们只需要最后一个值nex[-1],因为它表明了rev_s与s相互匹配的最大前缀长度。)
2、首先判断本身是不是回文
3、然后将s和r连接生成新的字符串l
4、循环判断l中最大前缀和后缀
5、最后只需要将rev_s的前k个字符与原始串s拼接即可,其中k是s的长度len(s)与p[-1]之差。
http://bookshadow.com/weblog/2015/05/22/leetcode-shortest-palindrome/
def shortestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
r = s[::-1]
if r == s:
return s
l = s+'#'+r
j = 0
nex = [0]*len(l)
for i in range(1,len(l)):
j = nex[i-1]
while j>0 and l[i]!=l[j]:
j = nex[j-1]
nex[i] = j + (l[i]==l[j])
return r[:len(r)-nex[-1]]+s
(97)336 Palindrome Pairs(Hard)
给定一个唯一单词列表,找到给定列表中的所有不同索引(i,j)对,以便两个单词的串联 i.e. words[i] + words[j]是一个回文
思路:
基本思想是检查每个单词的前缀(和后缀)本身是回文。如果您找到一个有效回文的前缀,那么反转的后缀可以与该词配对以形成回文。用一个例子可以更好地解释。
words = [“bot”, “t”, “to”]
从字符串“bot”开始。我们开始检查所有前缀。如果"", “b”, “bo”, "bot"他们自己是回文。空字符串和“b”是回文。我们使用相应的后缀(“bot”,“ot”)并检查它们的反转(“tob”,“to”)是否出现在我们的初始单词列表中。如果是的话(如字“to”),我们已经找到了有效的配对,其中逆转后缀可以预先考虑到当前单词,以便形成“to” +“BOT” =“tobot”。
https://leetcode.com/problems/palindrome-pairs/discuss/79209/Accepted-Python-Solution-With-Explanation
def palindromePairs(self, words):
"""
:type words: List[str]
:rtype: List[List[int]]
"""
word_dict = {}
res = []
for i in range(len(words)):
word_dict[words[i]] = i
for i in range(len(words)):
for j in range(len(words[i])+1):
temp1 = words[i][:j]
temp2 = words[i][j:]
if temp1[::-1] in word_dict and word_dict[temp1[::-1]]!=i and temp2[::-1] == temp2:
res.append([i,word_dict[temp1[::-1]]])
if j>0 and temp2[::-1] in word_dict and word_dict[temp2[::-1]]!=i and temp1[::-1]==temp1:
res.append([word_dict[temp2[::-1]],i])
return res
(98)131. Palindrome Partitioning(Medium)
给定字符串s,分区s使得分区的每个子字符串都是回文。 返回s的所有可能的回文分区。
思路:
1、使用递归
2、每次递归前先判断前面那个字符串是不是回文
def dfs(s,path):
if s=='':
self.res.append(path)
for i in range(1,len(s)+1):
if s[:i]==s[:i][::-1]:
dfs(s[i:],path + [s[:i]])
self.res = []
dfs(s,[])
return self.res
(99)132. Palindrome Partitioning II(Hard)
给定字符串s,分区s使得分区的每个子字符串都是回文。 返回s的回文分区所需的最小割数。
思路:
如果使用递归,会超时,考虑使用DP算法
用数组dp[i]记录从第0位到i位最小割数
使用i-1对第i个位置进行初始化,如果子串s[j:i]是回文串,则dp[i] = min(dp[i],dp[j]+1)
def minCut(self, s):
"""
:type s: str
:rtype: int
"""
n = len(s)
dp = range(-1,n)
for i in range(1, n + 1):
for j in range(i):
tmp = s[j:i]
if tmp == tmp[::-1]:
dp[i] = min(dp[i], dp[j] + 1)
return dp[n]
(100)267. Palindrome Permutation II(Medium)
给定一个字符串s,返回它的所有回文排列(没有重复)。如果没有形成回文排列,则返回一个空列表。 例如:
Given s = “aabb”, return [“abba”, “baab”].
Given s = “abc”, return [].
https://www.cnblogs.com/grandyang/p/5315227.html
思路:
使用字典存储每个字符的个数,如果字符个数是奇数超过两个,直接return []找出奇数个数的字符加入到mid
我们只需生成回文的前半段就好了,所以每个字符的个数都除以2,获得t,t就是前半段字符,只需要对其做全排列
还有一种情况需要注意,如果t中有重复字符,需要去重。
import collections
class Solution:
def generatePalindromes(s):
#边界条件
if len(s) ==0:
return []
#res结果
# counter所有字符统计量,
# p代表除以2之后的结果,
# odd存储奇数的字符
res = []
counter = collections.Counter(s)
p = []
odd = []
for i,v in counter.items():
if v%2:
odd +=[i]
p += [i]*(v//2)
if len(odd)>1:
return res
#有重复字符的全排列
def permutation(nums,path):
if len(nums) == 0:
res.append(''.join(path))
return
for i in range(len(nums)):
if i>0 and nums[i-1] == nums[i]:
continue
permutation(nums[:i]+nums[i+1:],path+[nums[i]])
#使用全排列递归,然后判断是否由奇数字符放在中间
permutation(p,[])
if odd:
res = [i+odd[0]+i[::-1] for i in res]
else:
res = [i + i[::-1] for i in res]
return res
print(Solution.generatePalindromes(''))
string(Parentheses)
(101)20. Valid Parentheses有效括号(Easy)
Given a string containing just the characters ‘(’, ‘)’, ‘{’, ‘}’, ‘[’ and ‘]’, determine if the input string is valid.
An input string is valid if:
Open brackets must be closed by the same type of brackets.
Open brackets must be closed in the correct order.
Note that an empty string is also considered valid.
思路:
1、使用压栈出栈的方法
def isValid(self, s):
"""
:type s: str
:rtype: bool
"""
dict = {')':'(','}':'{',']':'['}
parentheses = ""
for i in s:
if dict.get(i) ==None:
parentheses +=i
elif (len(parentheses)!=0) and (parentheses[-1] == dict.get(i)):
parentheses = parentheses[:-1]
else:
return False
if parentheses =='':
return True
else:
return False
(102)22. Generate Parentheses(Medium)
给定n对括号,编写一个函数来生成格式正确的括号的所有组合。
思路:
1、设定两个变量,代表左边和右边的括号数量
2、使用递归
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
def calculate(s,l,r):
if l==0 and r==0:
all_s.append(s)
if l>0:
calculate(s+'(',l-1,r)
if l<r:
calculate(s+')',l,r-1)
all_s =[]
if n>0:
calculate('',n,n)
return all_s
(103)32. Longest Valid Parentheses(Hard)
给定一个只包含字符’(‘和’)'的字符串,找到最长的有效(格式良好)括号子字符串的长度。
思路:
1、使用DP算法
2、遇到 ‘(’ 不一定合法
3、当i = ’)’ 时:分两种情况
当 i-1 = ‘(‘时,dp[i] = dp[i-2] +2
当 i-1 = ‘)’ 时,要找到 s[i - 1 - dp[i - 1]] 这个字符,判断它是否==’(’ 。且要加上dp[i-dp[i-1]-2]上的值
def longestValidParentheses(self, s):
"""
:type s: str
:rtype: int
"""
if len(s)==0:
return 0
dp = [0]*len(s)
for i in range(len(s)):
if i-1>=0 and s[i]==')':
if s[i-1]=='(':
if i-2>0:
dp[i] = dp[i-2]+2
else:
dp[i] = 2
elif s[i-1]==')':
if i-dp[i-1]-1>=0 and s[i-dp[i-1]-1]=='(':
if i-dp[i-1]-2>=0:
dp[i] = dp[i-dp[i-1]-2]+dp[i-1]+2
else:
dp[i] = dp[i-1]+2
return max(dp)
(104)241. Different Ways to Add Parentheses(Medium)
给定一系列数字和运算符,通过计算所有不同的组编号和运算符的方式返回所有可能的结果。有效的运算符是+, - 和*。
思路:
使用分治算法
并且使用memory记录已经算过的了。这样速度会快很多
def __init__(self):
self.memo = {}
def diffWaysToCompute(self, input):
"""
:type input: str
:rtype: List[int]
"""
if input.isdigit():
return [int(input)]
if input in self.memo:
return self.memo[input]
res = []
for i in range(len(input)):
if input[i] in '-+*':
r = self.diffWaysToCompute(input[:i])
l = self.diffWaysToCompute(input[i+1:])
res.extend([self.helper(j,k,input[i]) for j in r for k in l])
self.memo[input] = res
return res
def helper(self,m,n,op):
if op == '+':return m+n
if op == '-':return m-n
if op == '*':return m*n
(105)301. Remove Invalid Parentheses(Hard)
删除最小数量的无效括号,以使输入字符串有效。返回所有可能的结果。 注意:输入字符串可能包含括号(和)以外的字母。
思路:
从左到右判断,确保count[’(’]>=count[’)’]
- ## 如果count[")"]大于count[’(’] 那么就要循环result中所有元素,并且删除掉可能的’(’
## removed代表已经去掉的元素
## 使用循环每次弹出result中的一个结果,并将这个结果中删掉有可能的‘(’,将结果加入new_result
## 再将新的new_resulted赋予给resulted 且 remove +=1
然后从右到左判断,确保count[’(’]<=count[’)’]
*- ##也是使用同样的方法,只不过要注意末尾和开头
def removeInvalidParentheses(self, s):
"""
:type s: str
:rtype: List[str]
"""
removed = 0
results = {s}
count = {"(": 0, ")": 0}
#从左到右判断
for i, c in enumerate(s):
## 如果count[")"]大于count['('] 那么就要循环result中所有元素,并且删除掉可能的'('
## removed代表已经去掉的元素
## 使用循环每次弹出result中的一个结果,并将这个结果中删掉有可能的‘(',将结果加入new_result
## 再将新的new_resulted赋予给resulted 且 remove +=1
if c == ")" and count["("] == count[")"]:
new_results = set()
while results:
result = results.pop()
for j in range(i - removed + 1):
if result[j] == ")":
new_results.add(result[:j] + result[j + 1:])
results = new_results
removed += 1
else:
if c in count:
count[c] += 1
count = {"(": 0, ")": 0}
i = len(s)
ll = len(s) - removed
#removed表明之前已经去掉了的括号,所以现在results中最长是len(s)-removed
## ii代表当前运行到哪一步了,i代表S的当前
for ii in range(ll - 1, -1, -1):
i-=1
c = s[i]
if c == "(" and count["("] == count[")"]:
new_results = set()
while results:
result = results.pop()
for j in range(ii, ll):
if result[j] == "(":
new_results.add(result[:j] + result[j + 1:])
results = new_results
ll -= 1 #因为又去除了一个,所以再减去一
else:
if c in count:
count[c] += 1
return list(results)
(106)392. Is Subsequence(Medium)
给定字符串s和字符串t,检查s是否是t的子序列。 您可以假设s和t中只有小写英文字母。 t可能是一个非常长(长度〜= 500,000)的字符串,s是一个短字符串(<= 100)。字符串的子序列是一个新字符串,它是通过删除一些(可以是无)字符而不干扰其余字符的相对位置而由原始字符串形成的。
如果有很多传入的S,比如S1,S2,…,Sk,其中k> = 1B,并且你想逐个检查以查看T是否有其子序列。在这种情况下,您将如何更改代码?
思路:
就是S中相对位置不变,是否再t中存在,可以通过
很简单,遍历就好了
def isSubsequence(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
if s == '':
return True
if t =='':
return False
i = 0
j = 0
while i<len(s) and j<len(t):
if s[i]==t[j]:
i+=1
j+=1
return i ==len(s)
(107)115. Distinct Subsequences(Hard)
在S中,能找到几个T
给定字符串S和字符串T,计算S的不同子序列的数量,其等于T.
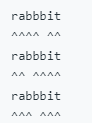
Input: S = “rabbbit”, T = “rabbit”
Output: 3
思路:使用动态规划DP,左边+(斜角(如果相等的话))res[i][j] = res[i][j-1] + (res[i-1][j-1] if s[j-1]==t[i-1] else 0)
def numDistinct(self, s, t):
"""
:type s: str
:type t: str
:rtype: int
"""
res = [[0 for _ in range(len(s)+1)] for _ in range(len(t)+1)]
res[0][0]=1
for j in range(1,len(s)+1):
res[0][j] = 1
for i in range(1,len(t)+1):
for j in range(1,len(s)+1):
res[i][j] = res[i][j-1] + (res[i-1][j-1] if s[j-1]==t[i-1] else 0)
print(res)
return res[len(t)][len(s)]
Math(基础)
(108)7. Reverse Integer(Easy)
给定32位有符号整数,整数的反向数字。
思路:
1、记得判断是正的还是负的
2、判断x是否越界
def reverse(self, x):
"""
:type x: int
:rtype: int
"""
sign = [1,-1][x<0]
x = sign*int(str(abs(x))[::-1])
if x<=(2**31)-1 and x>=-(2**31):
return x
else:
return 0
(109)165. Compare Version Numbers(Medium)
比较两个版本号version1和version2。 如果version1> version2返回1;如果version1 <version2返回-1;否则返回0。
思路:
1、使用split将数字分开
2、for循环最大的那个,小的用0补
3、比较两个数字的大小
def compareVersion(self, version1, version2):
"""
:type version1: str
:type version2: str
:rtype: int
"""
version1 = version1.split('.')
version2 = version2.split('.')
for i in range(max(len(version1),len(version2))):
##加int是因为可能会出现输入是01和1的情况
v1 = int(version1[i]) if i<len(version1) else 0
v2 = int(version2[i]) if i<len(version2) else 0
if v1<v2:
return -1
if v1>v2:
return 1
return 0
(110)66. Plus One(Easy)
给定表示非负整数的非空数字数组,加上整数的1。
存储数字使得最高有效数字位于列表的开头,并且数组中的每个元素包含单个数字。
您可以假设整数不包含任何前导零,除了数字0本身。
思路:
1、首先判断末尾是不是9,如果是,则变为0,i+1
2、如果不是9,则加一,返回
3、如果最后都是9,那就插入1在最前面
def plusOne(self, digits):
"""
:type digits: List[int]
:rtype: List[int]
"""
i = 1
while i<=len(digits):
if digits[-i] ==9:
digits[-i] =0
i+=1
else:
digits[-i] +=1
return digits
digits.insert(0,1)
return digits
(111)8. String to Integer (atoi) (Medium)
string 到 int
1、前面有n个空格 2、除空格外第一个必须为数字或者 - 或者 + 3、只输出数字 4、满足- 231~ 231-1
思路:
按照规格做就好,没什么难度
def myAtoi(self, str):
"""
:type str: str
:rtype: int
"""
ls = list(str.strip())
if len(ls) == 0 : return 0
sign = -1 if ls[0] == '-' else 1
if ls[0] in ['-','+'] : del ls[0]
ret, i = 0, 0
while i < len(ls) and ls[i].isdigit() :
ret = ret*10 + ord(ls[i]) - ord('0')
i += 1
return max(-2**31, min(sign * ret,2**31-1))
(112)258. Add Digits(Easy)
给定非负整数num,重复添加其所有数字,直到结果只有一位数。
你可以在O(1)运行时没有任何循环/递归吗?
思路:
思路一:
可以使用迭代+循环的方法
思路二:
N=(a[0] * 1 + a[1] * 10 + …a[n] * 10 n),令M = a[0] + a[1] + …a[n]
因为
1 % 9 = 1
10 % 9 = 1
100 % 9 = 1
所以 N % 9 = (a[0] + a[1] + …a[n])%9 = M%9 = (b[0] + b[1] + …b[n])%9 = O%9
又因为
9%9 = 0 为了防止这个问题的出现,我们可以(n-1)%9 +1
def addDigits(self, num: 'int') -> 'int':
if num == 0:
return 0
else:
return (num-1)%9+1
(113)67. Add Binary(Easy)
给定两个二进制字符串,返回它们的总和(也是二进制字符串)。
思路:
1、先将a,b加在一起转化为str
2、倒过来,判断是不是大于2,如果大于,则carry =1
3、循环完,记得判断carry是不是大于0,大于,则要在最前面加1
def addBinary(self, a, b):
"""
:type a: str
:type b: str
:rtype: str
"""
a = int(a)
b = int(b)
c = str(a+b)
d = ''
carry = 0
print(c)
for i in reversed(c):
num = int(i)+carry
print(num)
if num>=2:
# print(num)
num -=2
carry =1
else:
carry = 0
d = str(num)+d
if carry ==1:
d = '1'+d
return d
(114)43. Multiply Strings(Medium)
两个用字符串表示的非负数字,用字符串的方式返回他们的乘积。
Input: num1 = “123”, num2 = “456”
Output: “56088”
思路:
1、定义一个长度为len(num1)+len(num2),值为0的list
2、用嵌套for循环,注意进位可能大于10(进位包括前面运算出来的),要再用% and /
3、把s前面的0都去掉,最后把s join一下
def multiply(self, num1, num2):
"""
:type num1: str
:type num2: str
:rtype: str
"""
if num1=='0' or num2=='0':
return '0'
s =[0]*(len(num1)+len(num2))
for i in range(len(num2)-1,-1,-1):
add = 0
for j in range(len(num1)-1,-1,-1):
a = int(num2[i])*int(num1[j])+add
add = a/10 + (a%10+s[i+j+1])/10
s[i+j+1] = (a%10 +s[i+j+1])%10
s[i] = add
for i in range(len(s)):
if s[i] !=0:
s = s[i:]
break
return ''.join(str(i) for i in s)
(115)29. Divide Two Integers(Medium)
给定两个整数除数和被除数,除去两个整数而不使用乘法,除法和mod运算符。 将除数除以除数后返回商。 整数除法应截断为零。
思路:
1、先判断除数和被除数时候有其中一个为负(((dividend^divisor)>>31))
2、利用左移操作来实现出发过程。将一个数左移等于将一个数×2,取一个tmp = divisor,所以将除数tmp不断左移,直到其大于被除数dividend,然后得到dividend - tmp,重复这个过程。
3、返回 return max(-res,-2147483648) if ((dividend^divisor)>>31) else min(res,2147483647)
if abs(dividend) < abs(divisor):
return 0
ans = 0
while dividend >= divisor:
cnt = 1
tmp = divisor
while tmp << 2 < dividend:
cnt <<= 2
tmp <<= 2
ans += cnt
dividend -= tmp
return max(-res,-2147483648) if ((dividend^divisor)>>31) else min(res,2147483647)
(116)69. Sqrt(x)(Easy)
计算并返回x的平方根,其中x保证为非负整数。 由于返回类型是整数,因此将截断十进制数字,并仅返回结果的整数部分。
思路:
使用二分法来找,使用middle的平方来找
(x/2+1)^2>x
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
#because (x/2+1)^2>x
min_x =0
max_x = int((x/2) + 1)
while (max_x-min_x>=0):
middle = int((min_x+max_x)/2)
if middle**2 == x:
return middle
elif middle**2 <x:
min_x = middle+1
else:
max_x = middle-1
return max_x
(117)50. Pow(x, n)(Medium)
自己实现一个pow
思路:
使用连乘的方式会超时,所以使用右移的方式
m = abs(n)
ans = 1.0
while m:
if m &1:
ans *=x
x *=x
m >>=1
return ans if n>0 else 1/ans
(118)367. Valid Perfect Square(Easy)
给定正整数num,写一个函数,如果num是一个完美的正方形,则返回True,否则返回False。 注意:不要使用任何内置库函数,例如sqrt。
思路一:
使用二分法查找
def isPerfectSquare(self, num):
"""
:type num: int
:rtype: bool
"""
if num<1:
return False
if num ==1:
return True
start = 0
end = num
while end>=start:
mid = int((start+end)/2)
if mid*mid>num:
end = mid-1
elif mid*mid<num:
start = mid+1
else:
return True
return False
思路二:
使用牛顿法
牛顿法本身是一阶算法,本质是求根算法。但如果用来求最优解(极值点),这时就要求导
数为 0 的跟,就需要求二阶导数,就变成了二阶算法。
class Solution(object):
def mySqrt(self,x):
result = 1.0
while abs(result*result - x)>0.1:
result = (result+x/result)/2
return int(result)
(119)365. Water and Jug Problem(Medium)
你有两个容量为x和y升的水壶。有无限量的供水可供选择。您需要确定是否可以使用这两个水罐精确测量z升。
如果z升水是可测量的,那么在一端或两个桶中必须包含z升水
允许的操作:
用水完全填充任何水壶。
清空任何水壶。
将水从一个水壶倒入另一个水壶,直到另一个水壶完全充满或第一个水壶本身为空。
思路:
我们需要找到(m,n)使得 z = m*x + n*y
那么这两个(m,n)存在吗?
根据贝祖定理我们总是可以找到mx +ny = b,b = gcd(x,y) gcd means 最大公因数
如果z%b ==0,那么 m 和n就存在
def canMeasureWater(self, x, y, z):
"""
:type x: int
:type y: int
:type z: int
:rtype: bool
"""
return z ==0 or (x+y>=z and z%self.gcd(x,y)==0)
def gcd(self,x,y):
return x if y==0 else self.gcd(y,x%y)
(120)204. Count Primes(Easy)
计算小于非负数n的质数的数量。
Input: 10
Output: 4
Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
思路:
使用循环判断
1、如果s[i]是质数,那么从i*i之后每间隔i都不是质数,因为可以该数可以整除质数i
2、范围就是0~n0.5
def countPrimes(self, n):
"""
:type n: int
:rtype: int
"""
s = [1]*n
if n<3:
return 0
s[0] = s[1] = 0
for i in range(2,int(n**0.5)+1):
if s[i]==1:
s[i*i:n:i] = [0]*len(s[i*i:n:i])
return sum(s)
Math(SUM)
(121)1.Two Sum(easy)
给定一个整型数组,找出能相加起来等于一个特定目标数字的两个数。
给定一个整数数组,返回两个数字的索引,使它们相加到特定目标。 您可以假设每个输入只有一个解决方案,并且您可能不会两次使用相同的元素。
思路:建立一个字典,存储结果,然后在字典里面找
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
dict = {}
for i in range(len(nums)):
complement = target - nums[i]
if (dict.get(complement)!=None):
return [dict.get(complement),i]
else:
dict[nums[i]] = i
return None
(122)167. Two Sum II - Input array is sorted(Easy)
给定已按升序排序的整数数组,找到两个数字,使它们相加到特定的目标数。 函数twoSum应返回两个数字的索引,以便它们相加到目标,其中index1必须小于index2
您返回的答案(index1和index2)不是从零开始的。 您可以假设每个输入只有一个解决方案,并且您可能不会两次使用相同的元素
思路:
使用两个指针判断就好了
def twoSum(self, numbers, target):
"""
:type numbers: List[int]
:type target: int
:rtype: List[int]
"""
l = 0
r= len(numbers)-1
while(l<r):
if numbers[l]+numbers[r]==target:
return l+1,r+1
elif numbers[l]+numbers[r]>target:
r -=1
else:
l +=1
return None
(123)15. 3Sum(Medium)
给定n个整数的数组nums,是否有元素a,b,c在nums中,a + b + c = 0?找到数组中所有唯一的三元组,它们的总和为零。
思路:
1、首先给list排序(重点!!)
2、按顺序,如果list[i]>0,直接退出(因为排过序了)
3、如果list[i]==list[i-1],continue
4、定义b =i+1 ;e=len(list)。然后b++,e- -
5、b 和 e 也不能相同,如果用过了(因为题目要求唯一三元组)
def threeSum(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
nums.sort()
all = []
for i in range(len(nums)-2):
if nums[i]>0:
break
if i !=0 and nums[i]==nums[i-1]:
continue
b = i +1
e = len(nums)-1
while b<e:
sum = nums[b]+nums[e]+nums[i]
if sum>0:
e -=1
elif sum<0:
b +=1
else:
all.append([nums[i],nums[b],nums[e]])
while b<e and nums[b]==nums[b+1]:
b +=1
while b<e and nums[e]==nums[e-1]:
e -=1
b +=1
e -=1
return all
(124)16. 3Sum Closest
给定n个整数和整数目标的数组nums,在nums中找到三个整数,使得总和最接近目标。返回三个整数的总和。您可以假设每个输入都只有一个解决方案。
思路:
1、和15题解题方案有点像,只不过只需要一个输出
def threeSumClosest(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
out = nums[0]+nums[1]+nums[2]
nums.sort()
for i in range(len(nums)-2):
b = i+1
e = len(nums)-1
while b<e:
sum = nums[i]+nums[b]+nums[e]
if abs(sum-target)<abs(out-target):
out = sum
if sum-target>0:
e -=1
elif sum-target<0:
b +=1
else:
return out
return out
(125)18. 4Sum(Medium)
给定n个整数和整数目标的数组nums,是否有元素a,b,c和d在nums中,a + b + c + d = target?找到数组中所有唯一的四元组,它们给出了目标的总和。
思路:
和3sum差不多,只不过多了一层循环
def fourSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[List[int]]
"""
nums.sort()
all =[]
for i in range(len(nums)-3):
if i>0 and nums[i-1]==nums[i]:
continue
for j in range(i+1,len(nums)-2):
if j!=i+1 and nums[j-1]==nums[j]:
continue
b =j+1
e = len(nums)-1
while b<e:
sum = nums[i]+nums[j]+nums[e]+nums[b]
if sum>target:
e -=1
elif sum<target:
b +=1
else:
all.append([nums[i],nums[j],nums[b],nums[e]])
while b<e and nums[b]==nums[b+1]:
b +=1
while b<e and nums[e]==nums[e-1]:
e -=1
b+=1
e-=1
return all
Tree(基础)
(126)144 and 145. Binary Tree Postorder Traversal(Hard)
给定二叉树,返回其节点值的前、后序遍历。(使用迭代的方法)
思路:
前序遍历:1.根节点 2.左子树 3.右子树
中序遍历:1.左子树 2.根节点 3.右子树
后序遍历:1.左子树 2.右子树 3.根节点
有个前序、中序、后序的迭代操作(只是加入的顺序不一样,后序就差不多是前序的反向操作)
1、定义两个list,一个存储结果,一个存储访问过的结点
2、后序,在最前面插入结点(中间、右边、左边)(相当于前序反过来操作,因为在最前面插入)
def postorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
result = []
stack = []
p = root
while(p!=None or stack!=[]):
if p!=None:
result.insert(0,p.val)
stack.append(p)
p = p.right
else:
p = stack.pop()
p = p.left
return result
def preorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
cur = root
result = []
stack = []
while cur !=None or stack!=[]:
if cur!=None:
result.append(cur.val)
stack.append(cur)
cur = cur.left
else:
cur = stack.pop()
cur = cur.right
return result
(127)94. Binary Tree Inorder Traversal(Medium)
树的中序遍历
思路:
递归很容易实现
使用遍历的方法左-》中-》右
def inorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
stack = []
res = []
cur = root
while(cur!=None or stack!=[]):
if cur!=None:
stack.append(cur)
if cur.left !=None:
cur = cur.left
continue
cur = stack.pop()
res.append(cur.val)
cur = cur.right
return res
(128)102. Binary Tree Level Order Traversal(Medium)
给定二叉树,返回其节点值的级别顺序遍历。 (即,从左到右,逐级)。
思路:使用两个数组,其中一个数组存储当前层次的节点,另一个数组存储下一个层次的节点
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if root ==None:
return []
res = [root]
ans = []
while res:
temp = []
ans.append([i.val for i in res])
for node in res:
temp.append(node.left)
temp.append(node.right)
res = [i for i in temp if i]
return ans
Tree(Preorder)
(129)100. Same Tree(Easy)
给定两个二叉树,编写一个函数来检查它们是否相同。 如果两个二叉树在结构上相同并且节点具有相同的值,则认为它们是相同的。
思路:
均使用递归来判断
def isSameTree(self, p, q):
"""
:type p: TreeNode
:type q: TreeNode
:rtype: bool
"""
if not p and not q:
return True
if not p or not q:
return False
if p.val !=q.val:
return False
return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
(130)101. Symmetric Tree(Easy)
给定二叉树,检查它是否是自身的镜像(即,围绕其中心对称)。
思路:
1、使用递归
2、每次判断左子树和右子树是不是对称的,再判断左子树和右子树的值是否相同
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root:
return True
def check(r1,r2):
if not r1 and not r2:
return True
if not r1 or not r2:
return False
a1= check(r1.left,r2.right)
a2 = check(r1.right,r2.left)
return a1 and a2 and (r1.val==r2.val)
return check(root.left,root.right)
(131)226. Invert Binary Tree(Easy)
反转二叉树
思路:
使用递归,分别反转左节点和右节点的子集,然后左节点和右节点交换
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root ==None:
return root
left = right = None
if root.left !=None:
left = self.invertTree(root.left)
if root.right != None:
right = self.invertTree(root.right)
root.left = right
root.right = left
return root
(132)257. Binary Tree Paths(Easy)
Given a binary tree, return all root-to-leaf paths.
Note: A leaf is a node with no children.
思路:
使用递归,分别访问左节点和右节点,如果递归之后是叶子结点,就加入路径中
def dfs(self,l,root,s):
if root.left ==None and root.right==None:
l.append(s)
return;
if root.left !=None:
self.dfs(l,root.left,s+'->'+str(root.left.val))
if root.right !=None:
self.dfs(l,root.right,s+'->'+str(root.right.val))
def binaryTreePaths(self, root: 'TreeNode') -> 'List[str]':
l =[]
if root==None:
return l
self.dfs(l,root,str(root.val))
return l
(133)112. Path Sum(Easy)
给定二叉树和求和,确定树是否具有根到叶路径,使得沿路径的所有值相加等于给定的总和。
思路:
1、使用递归
def hasPathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: bool
"""
if root ==None:
return False
if (root.left==root.right==None):
return sum == root.val
else:
return self.hasPathSum(root.left,sum-root.val) or self.hasPathSum(root.right,sum-root.val)
(134)113. Path Sum II(Medium)
给定一个二叉树的总和,发现其中每个路径的总和等于给定的款项的所有根到叶的路径。
思路:使用递归,难度不大,就是陷阱比较多,注意几个point
- 一定要叶节点为结尾
- 节点的值可能有负数,不能碰到和为0时,退出
def pathSum(self, root, sum):
res = []
def dfs(sum,root,path):
if not root:
return
elif sum - root.val ==0:
if not root.left and not root.right:
res.append(path+[root.val])
return
dfs(sum-root.val,root.left,path+[root.val])
dfs(sum-root.val,root.right,path+[root.val])
dfs(sum,root,[])
return res
(135)129. Sum Root to Leaf Numbers(Medium)
Input: [1,2,3]
1
/
2 3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.
找到所有根到叶数的总和。
使用递归
def sumNumbers(self, root):
"""
:type root: TreeNode
:rtype: int
"""
def dfs(root,sum_n):
if root:
dfs(root.left,sum_n*10+root.val)
dfs(root.right,sum_n*10+root.val)
if not root.left and not root.right:
self.res += sum_n*10+root.val
self.res = 0
dfs(root,0)
return self.res
(136)298 Binary Tree Longest Consecutive Sequence(Medium)
给定二叉树,找到最长连续序列路径的长度。
该路径指的是沿着父子连接从树中的某个起始节点到任何节点的任何节点序列。最长的连续路径需要从父到孩子(不能反过来)
思路:
最长连续子序列必须从root到leaf的方向,比如 1->2,返回长度2, 比如1->3->4->5,返回3->4->5这个子序列的长度3。
使用递归,递归的时候传入父亲节点的值,还要传入一个变量用于记录当前长度
self.max_len = 0
def longestConsecutive(self,root):
self.dfs(root,0,0)
return self.max_len
def dfs(self,root,last_value,cur_len):
if root:
if root.val == last_value+1:
cur_len +=1
else:
cur_len =1
max_len = max(max_len,cur_len)
self.dfs(root.left,root.val,cur_len)
self.dfs(root.right,root.val,cur_len)
(137)111. Minimum Depth of Binary Tree(Easy)
给定二叉树,找到它的最小深度。
思路:
1、使用递归
2、左边和右边比最小
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
def D(root,minmum):
if not root:
return 2**31 -1
if root.left ==root.right==None:
return minmum
lm = D(root.left,minmum+1)
rm = D(root.right,minmum+1)
return min(lm,rm)
if root ==None:
return 0
return D(root,1)
Tree(Postorder)
(138)104. Maximum Depth of Binary Tree(Easy)
给定二叉树,找到它的最大深度。
思路:
使用递归方法
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
left = self.maxDepth(root.left)
right = self.maxDepth(root.right)
return max(left,right)+1
(139)110. Balanced Binary Tree(Easy)
给定二叉树,确定它是否是高度平衡的。
思路:
1、使用DFS,在传递的时候,要加上height
2、如果right、left其中一个是False,就返回False。
3、如果right、left相差大于1,返回False
def isBalanced(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if root == None:
return True
def B(root,height):
if not root:
return height-1
if root.left == root.right ==None:
return height
lheight = B(root.left,height+1)
rheight = B(root.right,height+1)
if rheight==False or lheight==False:
return False
if abs(lheight-rheight)>1:
return False
return max(lheight,rheight)
return True if B(root,1) else False
(140)124. Binary Tree Maximum Path Sum(Hard)
给定非空二叉树,找到最大路径总和。
对于此问题,路径定义为沿着父子连接从树中的某个起始节点到任何节点的任何节点序列。该路径必须至少包含一个节点,并且不需要通过根节点。
思路:
1、使用递归,需要设置一个全局变量,用来随时更新最大值(这个最大值是根节点加上左右节点)
2、返回当前节点加上左右其中一个最大值。(这个最大值是根节点,加上左右其中一个)
3、注意:全局变量刚开始不能设为0,因为可能出现所有节点都为负的情况,然后题目要求至少要输出一个节点
def maxPathSum(self, root):
"""
:type root: TreeNode
:rtype: int
"""
def dfs(root):
if not root:
return 0
left = dfs(root.left)
right = dfs(root.right)
self.max = max(self.max,root.val+left+right)
return max(0,root.val+max(left,right))
##self.max 不能设为0,因为可能只有root.val = -3的情况
self.max = None
dfs(root)
return self.max
(141)250 Count Univalue Subtrees(Medium)
给定二叉树,计算唯一子树的数量
唯一子树:子树里面每个值都一样
思路:
是一个自下往上的递归的过程。之所以是自下往上,是因为只要一颗子树不是univalue的,那么任何包含这颗子树的树都不是univalue的。同样的,uni value本身也是具备传递性的,也就是说如果某一个子树是univalue的,那么它的父亲节点只需要和这个子树的根节点进行比较就可以了,因为整个树的值都是一样的。
所以整个算法基本就是,先往左右要结果,满足以下条件的为univalue subtree
- 左子树为空或者左子树为univalue subtree并且当前节点和左子树根节点值相同
- 右子树为空或者右子树为univalue subtree并且当前节点和左子树根节点值相同
空节点我们也可以认为是一个univalue subtree。
当一个子树被判定为univalue subtree的时候就在计数器加一即可。
def countUnivalSubtrees(self,root):
self.result = 0
self.dfs(root)
return self.result
def dfs(self,root):
if not root:
return True
else:
left = self.dfs(root.left)
right = self.dfs(root.right)
if (left and (root.left == None or root.left.val == root.val)) and right and (root.right==None or root.right.val==root.val)):
self.result +=1
(142)366. Find Leaves of Binary Tree(Medium)
给定一个二叉树,收集树的节点,就好像你这样做:收集并删除所有叶子,重复直到树为空
思路:
每一个节点从左子节点和右子节点分开走可以得到两个深度,由于成为叶节点的条件是左右子节点都为空,所以我们取左右子节点中较大值加1为当前节点的深度值,知道了深度值就可以将节点值加入到结果res中的正确位置了
时间复杂度分析:每个结点只访问一次 O(n)
def findLeaves(self,root):
self.list = []
self.dfs(root)
def dfs(self,root):
if root:
left = self.dfs(root.left)
right = self.dfs(root.right)
k = max(left,right)+1
if len(self.list) <=k:
self.list.append([])
self.list[k].append(root)
return k
return -1
(143)337 House Robber III(Medium)
小偷又发现了自己盗窃的新地方。这个区域只有一个入口,称为“根”。除了根,每个房子只有一个或一个父母的房子。巡回演出后,聪明的小偷意识到“这个地方的所有房屋都形成了一棵二叉树”。如果两个直接连接的房屋在同一个晚上被闯入,它将自动联系警方。
确定小偷今晚可以抢劫的最大金额而不警告警察。
思路:
返回现在最大的,和上一次最大的
now:如果当前结点被盗,挣到的最大money
later:如果当前结点没有被盗,挣到的最大money
now = node.val + left[1] +right [1]
later = max(left)+max(right)
def rob(self, root):
"""
:type root: TreeNode
:rtype: int
"""
return max(self.rob_dfs(root))
def rob_dfs(self,root):
if not root:
return [0,0]
left = self.rob_dfs(root.left)
right = self.rob_dfs(root.right)
now = root.val + left[1] + right[1]
later = max(left)+max(right)
return [now,later]
Tree(BFS)
(144)107. Binary Tree Level Order Traversal II(Easy)
给定二叉树,返回其节点值的自下而上级别顺序遍历。 (即,从左到右,逐层逐层)。
思路:
和102一样,只不过最后把数组倒过来就好了
def levelOrderBottom(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if root ==None:
return []
res = [root]
ans = []
while res:
temp = []
ans.append([i.val for i in res])
for node in res:
temp.append(node.left)
temp.append(node.right)
res = [i for i in temp if i]
return ans[::-1]
(145)103. Binary Tree Zigzag Level Order Traversal(Medium)
给定二叉树,返回其节点值的Z字形级别遍历。 (即,从左到右,然后从右到左进行下一级别并在之间交替)。
思路:102题的思想,然后增加一个变量flag=1 每次循环一遍flag*=-1
def zigzagLevelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root:
return []
res = [root]
ans = []
flag = 1
while res:
ans.append([i.val for i in res][::flag])
temp = []
for node in res:
temp.append(node.left)
temp.append(node.right)
res = [i for i in temp if i]
flag *=-1
return ans
(146)199. Binary Tree Right Side View(Medium)
给定一个二叉树,想象自己站在它的右侧,返回从上到下排序的节点的值。
思路:
使用循环操作,选取最后一个
def rightSideView(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
if not root:
return []
res = [root]
ans = []
while(res):
ans.append(res[-1].val)
res = [k for node in res for k in (node.left,node.right) if k ]
return ans
Tree(BST)
(147)98. Validate Binary Search Tree(Medium)
Given a binary tree, determine if it is a valid binary search tree (BST).
思路:
使用递归,怎么设定这个子树的最大最小值是关键(要均在最大最小值之间)。对于没有最大最小值用None来表示
def isValidBST(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root:
return True
def dfs(root,lower,upper):
if lower !=None and root.val<= lower:
return False
if upper !=None and root.val>=upper:
return False
left = dfs(root.left,lower,root.val) if root.left else True
if (left):
right = dfs(root.right,root.val,upper) if root.right else True
return right
else:
return False
return dfs(root,None,None)
(148)235. Lowest Common Ancestor of a Binary Search Tree(Easy)
给定二叉搜索树(BST),找到BST中两个给定节点的最低共同祖先(LCA)。
根据维基百科上LCA的定义:“最低共同祖先在两个节点p和q之间定义为T中的最低节点,其中p和q都是后代(我们允许节点成为其自身的后代)。 ”
思路:
可以使用递归和迭代两种方式
1、如果两个结点都小于当前结点,走左边
2、如果两个结点都大于当前结点,走右边
3、否则输出当前结点
#Recursive Approach space O(n) Time O(n)
# if p.val > root.val and q.val>root.val:
# return self.lowestCommonAncestor(root.right,p,q)
# elif p.val<root.val and q.val<root.val:
# return self.lowestCommonAncestor(root.left,p,q)
# else:
# return root
#iterative
while root:
if p.val>root.val and q.val>root.val:
root = root.right
if p.val<root.val and q.val<root.val:
root = root.left
else :
return root
(149)236. Lowest Common Ancestor of a Binary Tree(Medium)
给定二叉树,找到树中两个给定节点的最低共同祖先(LCA)。
根据维基百科上LCA的定义:“最低共同祖先在两个节点p和q之间定义为T中的最低节点,其中p和q都是后代(我们允许节点成为其自身的后代)。 ”
没有做小右大得规矩了
思路:
使用递归,如果左右两个结点+中间节点有大于等于两个,那就是该节点
class Solution:
def __init__(self):
# Variable to store LCA node.
self.ans = None
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
def recurse_tree(current_node):
# If reached the end of a branch, return False.
if not current_node:
return False
# Left Recursion
left = recurse_tree(current_node.left)
# Right Recursion
right = recurse_tree(current_node.right)
# If the current node is one of p or q
mid = current_node == p or current_node == q
# If any two of the three flags left, right or mid become True.
if mid + left + right >= 2:
self.ans = current_node
# Return True if either of the three bool values is True.
return mid or left or right
# Traverse the tree
recurse_tree(root)
return self.ans
(150)108. Convert Sorted Array to Binary Search Tree(Easy)
给定一个数组,其中元素按升序排序,将其转换为高度平衡的BST。
思路:
1、当len(nums)<=2时,赋值返回
2、使用二分法来建立树
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if len(nums)==0:
return None
elif len(nums)==1:
return TreeNode(nums[0])
elif len(nums)==2:
root = TreeNode(nums[0])
root.right = TreeNode(nums[1])
else:
middle = int((len(nums)-1)/2)
root = TreeNode(nums[middle])
root.left = self.sortedArrayToBST(nums[:middle])
root.right = self.sortedArrayToBST(nums[middle+1:])
return root
(151)109. Convert Sorted List to Binary Search Tree(Medium)
给定单个链接列表,其中元素按升序排序,将其转换为高度平衡的BST。
思路:
1、先将链表转化为数组
2、然后采用150题的思路
def sortedListToBST(self, head):
"""
:type head: ListNode
:rtype: TreeNode
"""
array = []
while head:
array.append(head.val)
head = head.next
def dfs(nums):
n = len(nums)
if n ==0:
return None
if n ==1:
return TreeNode(nums[0])
if n ==2:
root = TreeNode(nums[0])
root.right = TreeNode(nums[1])
return root
middle = (n-1)//2
root = TreeNode(nums[middle])
root.left = dfs(nums[:middle])
root.right = dfs(nums[middle+1:])
return root
return dfs(array)
(152)173. Binary Search Tree Iterator(Medium)
在二叉搜索树(BST)上实现迭代器。您的迭代器将使用BST的根节点进行初始化。 调用next()将返回BST中的下一个最小数字。
思路:
1、要加一个函数读取当前最小
2、使用stack进行存储
3、先把左边的加入,然后左边没有了再加入右边
class BSTIterator(object):
def __init__(self, root):
"""
:type root: TreeNode
"""
self.stack = []
self.addmin(root)
def next(self):
"""
@return the next smallest number
:rtype: int
"""
tempNode = self.stack.pop()
self.addmin(tempNode.right)
return tempNode.val
def hasNext(self):
"""
@return whether we have a next smallest number
:rtype: bool
"""
return self.stack
def addmin(self,node):
while node is not None:
self.stack.append(node)
node = node.left
(153)230. Kth Smallest Element in a BST(Medium)
给定二叉搜索树,编写函数kthSmallest以找到其中的第k个最小元素。 注意: 您可以假设k始终有效,1≤k≤BST的总元素。
思路:
可是使用递归,也可以使用迭代
def kthSmallest(self, root, k):
"""
:type root: TreeNode
:type k: int
:rtype: int
"""
stack = []
while True:
while root:
stack.append(root)
root = root.left
root = stack.pop()
k -=1
if not k:
return root.val
root = root.right
(154)297. Serialize and Deserialize Binary Tree(Hard)
序列化是将数据结构或对象转换为位序列的过程,以便将其存储在文件或内存缓冲区中或者通过网络连接链路传输,以便稍后在相同或另一个计算机环境中重建。
设计一种算法来序列化和反序列化二叉树。序列化/反序列化算法的工作方式没有限制,您只需要确保二进制树可以序列化为字符串,并且可以将此字符串反序列化为原始树结构
澄清:以上格式与LeetCode序列化二叉树的方式相同。您不一定需要遵循这种格式,因此请发挥创意并自己提出不同的方法。
注意:不要使用类成员/全局/静态变量来存储状态。您的序列化和反序列化算法应该是无状态的。
思路:
就是个解码编码得问题
使用递归
class Codec:
def serialize(self, root):
"""Encodes a tree to a single string.
:type root: TreeNode
:rtype: str
"""
def re_se(node):
if node:
res.append(node.val)
re_se(node.left)
re_se(node.right)
else:
res.append('#')
res = []
re_se(root)
return res
def deserialize(self, data):
"""Decodes your encoded data to tree.
:type data: str
:rtype: TreeNode
"""
def re_de():
r = next(res)
if r =='#':
return None
node = TreeNode(r)
node.left = re_de()
node.right = re_de()
return node
res = iter(data)
return re_de()
(155)285. Inorder Successor in BST(Medium)
给定二叉搜索树及其中的节点,在BST中找到该节点的有序后继。 节点p的后继者是具有大于p.val的最小密钥的节点。
思路:
返回某个节点中序的下一个节点
def inorderSuccessor(self,root,p):
if root and p:
ans = None
while root:
if root.val>p.val:
ans = root
root = root.left
else:
root = root.right
return ans
return None
(156)270: Closest Binary Search Tree Value(Easy)
给定非空二进制搜索树和目标值,找到BST中最接近目标的值。
注意: 给定目标值是浮点数。 保证BST中只有一个最接近目标的唯一值。
思路:
先定义一个最小值和靠近目标的点
然后使用循环和BST的特性寻找该最小值
def closestValue(self,root,target):
if not root:
return None
ans = abs(root.val - target)
ans_value = root.val
while True:
if abs(target - root.val)<ans:
ans = abs(target - root.val)
ans_value = root.val
if target<root.val and root.left:
root = root.left
elif target>root.val and root.right:
root = root.right
else:
break
return ans_value
(157)272. Closest Binary Search Tree Value II(Medium)
给定非空二进制搜索树和目标值,在BST中找到最接近目标的k值。
注意: 给定目标值是浮点数。 您可以假设k始终有效,即:k≤总节点数。 保证BST中只有一组唯一的k值最接近目标。
跟进: 假设BST是平衡的,你能在低于O(n)运行时间(其中n =总节点)解决它吗?
思路:
中序遍历,如果数组不到K个,直接加入res,中序遍历代表数据是从小到大的
如果节点与目标值的差值绝对值小于结果res首元素与目标值之差的绝对值,则删除首元素,然后加入末位
否则直接退出
def closestKValues(root,target,k):
res = []
s = []
while(root or s):
while root:
s.insert(0,root)
root = root.left
root = s.pop()
if len(res)<k:
res.append(root.val)
elif abs(root.val-target) <abs(res[0]-target):
res = res[1:]
res.append(root.val)
else:
break
root = root.right
return res
(158)99. Recover Binary Search Tree(Hard)
Two elements of a binary search tree (BST) are swapped by mistake.Recover the tree without changing its structure.
思路:
使用中序遍历递归(是递增序列),用pre来存储中序遍历的前一个变量(全局的)总共有两种情况:
1,相邻的换(只出现一个逆序对)只需将前后两个值记下,然后进行交换
2,不相邻的换(出现两个逆序对)需要记下第一次的第一个,和第二次的第二个值,然后交换
def recoverTree(self, root):
"""
:type root: TreeNode
:rtype: None Do not return anything, modify root in-place instead.
"""
self.first=None
self.second = None
self.pre = None
def dfs(root):
if root ==None:
return
dfs(root.left)
if self.pre and self.pre.val>root.val:
if self.first ==None:
self.first,self.second = self.pre,root
else:
self.second = root
self.pre = root
dfs(root.right)
dfs(root)
self.first.val,self.second.val = self.second.val,self.first.val
Tree(重要)
(159)116. Populating Next Right Pointers in Each Node(Medium)
您将获得一个完美的二叉树,其中所有叶子都在同一级别,每个父级都有两个孩子。填充每个下一个指针以指向其下一个右侧节点。如果没有下一个右节点,则下一个指针应设置为NULL。 最初,所有下一个指针都设置为NULL
思路:
def connect(self, root):
"""
:type root: Node
:rtype: Node
"""
if not root:
return root
pre = root
cur = None
while(pre.left):
cur = pre
while(cur):
cur.left.next = cur.right
if cur.next:
cur.right.next = cur.next.left
cur = cur.next
pre = pre.left
return root
(160)117.Populating Next Right Pointers in Each Node II(Medium)
思路:
和116一样,只不过要多加一个判断,下一行的最左边的元素
def connect(self, root):
"""
:type root: Node
:rtype: Node
"""
pre = root
cur = []
while(pre):
#加一个判断,判断最左边的元素
cur = pre
now = None
while not now and cur:
if cur.left !=None:
now = cur.left
elif cur.right !=None:
now = cur.right
else:
cur = cur.next
pre = now
while cur:
if cur.left and cur.left !=now:
now.next = cur.left
now = cur.left
if cur.right and cur.right !=now:
now.next = cur.right
now = cur.right
cur = cur.next
return root
(161)314. Binary Tree Vertical Order Traversal(Medium)
给定二叉树,返回其节点值的垂直顺序遍历。 (即,从上到下,逐列)。 如果两个节点位于同一行和列中,则顺序应为从左到右。
思路:
使用BFS+字典,设置根节点为0,左节点列为-1,右节点为1,然后使用广度优先搜索。
def vertivalOrder(self,root):
if not root:
return []
cols = collections.defaultdict(list)
q = [(root,0)]
while q:
new_q = []
for node,col in q:
cols[col].append(node.val)
if node.left:
new_q.append((node.left,col-1))
if node.right:
new_q.append((node.right,col+1))
q = new_q
return [cols[col] for col in sorted(cols.keys())]
(162)96. Unique Binary Search Trees(Medium)
Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?
思路:
使用dp算法
//由1,2,3,...,n构建的二叉查找树,以i为根节点,左子树由[1,i-1]构成,其右子树由[i+1,n]构成。
//定义f(i)为以[1,i]能产生的Unique Binary Search Tree的数目
//若数组为空,则只有一种BST,即空树,f(0)=1;
//若数组仅有一个元素1,则只有一种BST,单个节点,f(1)=1;
//若数组有两个元素1,2,则有两种可能,f(2)=f(0)*f(1)+f(1)*f(0);
//若数组有三个元素1,2,3,则有f(3)=f(0)*f(2)+f(1)*f(1)+f(2)*f(0)
//由此可以得到递推公式:f(i)=f(0)*f(i-1)+...+f(k-1)*f(i-k)+...+f(i-1)*f(0)
代码:
def numTrees(self, n):
"""
:type n: int
:rtype: int
"""
res = [0 for _ in range(n+1)]
res[0] =1
res[1] =1
for i in range(2,n+1):
for j in range(0,i):
res[i] += res[j]*res[i-j-1]
return res[n]
Backtracking(基础)
(163)78. Subsets(Medium)
给定一组不同的整数,nums,返回所有可能的子集(幂集)。
使用递归,还无需判断条件
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
def dfs(nums,path,begin):
res.append(path)
for i in range(begin,len(nums)):
dfs(nums,path+[nums[i]],i+1)
res = []
dfs(nums,[],0)
return res
(164)90.Subsets II(Medium)
给定可能包含重复项,nums的整数集合,返回所有可能的子集(幂集)。
思路:
1、使用递归,当出现有重复元素,使用判断if k>i and nums[k]==nums[k-1]
2、记得要对元素进行排序
def subsetsWithDup(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res = []
nums.sort()
def dfs(i, path):
res.append(path)
for k in range(i,len(nums)):
if k>i and nums[k-1]==nums[k]:
continue
dfs(k+1,path +[nums[k]])
dfs(0,[])
return res
(165)77. Combinations(Medium)
Given two integers n and k, return all possible combinations of k numbers out of 1 … n.
利用递归
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
res = []
def dfs(begin,end,k,path):
if len(path)==k:
res.append(path)
return
for i in range(begin,end):
dfs(i+1,end,k,path+[i])
dfs(1,n+1,k,[])
return res
(166)39. Combination Sum(Medium)
给定一组候选数字(候选者)(没有重复)和目标数量(目标),找到候选人数总和目标的候选人中的所有独特组合。
可以从候选者无限次数中选择相同的重复数字。
注意: 所有数字(包括目标)都是正整数。 解决方案集不得包含重复的组合。
思路:
1、使用DFS
2、记得排序
def combinationSum(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
def dfs(target,path,k):
if target<0:
return
if target==0:
res.append(path)
return
for i in range(k,len(candidates)):
dfs(target-candidates[i],path+[candidates[i]],i)
if target-candidates[i]<=0:
break
res = []
candidates.sort()
dfs(target,[],0)
return res
(167)40. Combination Sum II(Medium)
给定候选数字(候选者)和目标数量(目标)的集合,找到候选人数量总和为目标的候选人中的所有独特组合。
候选人中的每个号码只能在组合中使用一次。 注意: 所有数字(包括目标)都是正整数。 解决方案集不得包含重复的组合。
思路:要判断当i>k时 并且candidates[i-1] == candidates[i],要退出
其它和39题类似
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
def dfs(path,target,k):
if target<0:
return
if target==0:
# if path not in res:
res.append(path)
return
for i in range(k,len(candidates)):
if i>k and candidates[i-1] == candidates[i]:
continue
dfs(path+[candidates[i]],target-candidates[i],i+1)
if target-candidates[i]<=0:
break
res = []
candidates.sort()
dfs([],target,0)
return res
(168)216. Combination Sum III(Medium)
找到所有可能的k个数字组合,它们加起来为n,假设只能使用1到9的数字,并且每个组合应该是一组唯一的数字。
注意: 所有数字都是正整数。 解决方案集不得包含重复的组合。
思路:
使用递归,使用减法操作,就无需用sum了
def combinationSum3(self, k, n):
"""
:type k: int
:type n: int
:rtype: List[List[int]]
"""
def dfs(begin,end,k,n,path):
if k == 0:
if n ==0:
res.append(path)
else:
return
for i in range(begin,end):
dfs(i+1,end,k-1,n-i,path+[i])
res = []
dfs(1,min(n+1,10),k,n,[])
return res
(169)377. Combination Sum IV(Medium)
给定具有所有正数且没有重复的整数数组,找到加到正整数目标的可能组合的数量。
思路:
dp[i]表示目标数为i的解的个数,从1遍历到target,对于每一个数i,遍历nums数组,如果i>=x, dp[i] += dp[i - x]。比如说对于[1,2,3] 4,这个例子,当我们在计算dp[3]的时候,3可以拆分为1+x,而x即为dp[2],3也可以拆分为2+x,此时x为dp[1],3同样可以拆为3+x,此时x为dp[0],我们把所有的情况加起来就是组成3的所有情况了。
def combinationSum4(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
dp = [0]*(target+1)
dp[0] = 1
for i in range(1,target+1):
for a in nums:
if i>=a:
dp[i] += dp[i-a]
return dp[target]
(170)254. Factor Combinations(Medium)
数字可以被视为factor的产物。例如,8 = 2 x 2 x 2 = 2 x 4.
编写一个取整数n的函数并返回其factor的所有可能组合。
每个组合的因子必须按升序排序,例如:2和6的因子是[2,6],而不是[6,2]。 你可以假设n总是正的。 因素应大于1且小于n。
思路:
使用递归,如果n==1,并且len(path)>1,则加入
如果n%i ==0 则输入i,int(n/i),path+[i]
class Solution:
def getfactor(self,n):
self.res = []
self.helper(2,n,[])
return self.res
def helper(self,start,n,path):
if n ==1:
if len(path)>1:
self.res.append(path)
return
for i in range(start,n+1):
if n%i == 0:
self.helper(i,int(n/i),path+[i])
(171)46. Permutations(Medium)
全排列问题
Given a collection of distinct integers, return all possible permutations.
思路:使用递归dfs,没啥难度
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
def dfs(nums,path):
if len(nums)==0:
res.append(path)
for i in range(len(nums)):
dfs(nums[:i]+nums[i+1:],path+[nums[i]])
res = []
dfs(nums,[])
return res
(172)47. Permutations II(Medium)
全排列问题,加上了有重复数字
思路:首先先排序,使用递归之后,加上判断,如果后一个与前一个相同,则跳过
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
def dfs(nums,path):
if len(nums)==0:
res.append(path)
for i in range(len(nums)):
if i>0 and nums[i]==nums[i-1]:
continue
dfs(nums[:i]+nums[i+1:],path+[nums[i]])
nums.sort()
res = []
dfs(nums,[])
return res
(173)31. Next Permutation(Medium)
产生下一个序列,对给定序列进行重排,生成一个字母顺序比它更大的下一个序列。
如果给定的序列已经是按字母顺序排列中最大的一个了,则进行逆序排列。
算法在数组内进行,不要使用额外空间。
思路:
i = len -2 j = len-1
1、从后往前遍历,i 找到第一个不满足升序的元素;如果都是升序,则i为-1(从后往前看的升序)
2、当 j>i 时,找到一个 j 的值大于 i 的,然后和 i 交换
3、将 i 之后的元素进行排序操作
def nextPermutation(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
if not nums: return nums
l = len(nums)
i, j = l - 2, l - 1
while i >= 0 and nums[i] >= nums[i+1]:
i -= 1
while j > i and nums[j] <= nums[i]:
j -= 1
nums[i], nums[j] = nums[j], nums[i]
nums[i+1:] = sorted(nums[i+1:])
(174)60. Permutation Sequence(Medium)
Given n and k, return the kth permutation sequence.
思路:
使用了除法,还是需要使用int,不然就是float类型。//也不行
def getPermutation(self, n, k):
nums = [str(i) for i in range(1, n + 1)]
k -= 1
factor = 1
res = []
# 计算排列
for i in range(1, n):
factor *= i
for i in reversed(range(n)):
res.append(nums[int(k / factor)])
nums.remove(nums[int(k / factor)])
if i != 0:
k %= factor
factor /= i
return ''.join(res)
(175)291. Word Pattern II 词语模式 II(Medium)
Given a pattern and a string str, find if str follows the same pattern.
Here follow means a full match, such that there is a bijection between a letter in pattern and a non-empty substring in str.
Examples:
pattern = “abab”, str = “redblueredblue” should return true.
pattern = “aaaa”, str = “asdasdasdasd” should return true.
pattern = “aabb”, str = “xyzabcxzyabc” should return false.
思路:
可以用回溯法来判断每一种情况,用哈希表建立模式字符和单词之间的映射,还需要用变量p和r来记录当前递归到的模式字符和单词串的位置,在递归函数中,如果p和r分别等于模式字符串和单词字符串的长度,说明此时匹配成功结束了,返回ture,反之如果一个达到了而另一个没有,说明匹配失败了,返回false。
1、判断时候都达到了末尾
2、如果没有达到末尾,判断patten[i]有没有在字典中,如果有,则判断词与str中下一个词是否匹配
3、如果patten[i]不在字典中,则循环str
def wordpatternMatch(self,pattern,str):
w2p,p2w = {},{}
return self.match(pattern,str,0,0,w2p,p2w)
def match(self,pattern,str,i,j,w2p,p2w):
is_match = False
if i==len(pattern) and j==len(str)
is_match = True
elif i<len(pattern) and j<len(str):
p = pattern[i]
if p in p2w:
w = p2w[p]
if w == str[j:j+len(w)]:
is match = self.match(pattern,str,i+1,j+len(w),w2p,p2w)
else:
for k in range(j,len(str)):
w = str[j:k+1]
if w not in w2p:
w2p[w],p2w[p] = p,w
is_match = self.match(pattern,str,i+1,k+1,w2p,p2w)
w2p.pop(w),p2w.pop(p)
if is_match:
break
return is_match
(176)17. Letter Combinations of a Phone Number(Medium)
给定包含2-9(含)的数字的字符串,返回该数字可能表示的所有可能的字母组合。(不包含1)
思路:
1、使用递归
2、将当前的和之后生成的进行组合
def letterCombinations(self, digits):
"""
:type digits: str
:rtype: List[str]
"""
mapping = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
'6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
if len(digits)==0:
return []
if len(digits) ==1:
return list(mapping[digits[0]])
l = self.letterCombinations(digits[:-1])
return [a+c for a in l for c in mapping[digits[-1]]]
(177)320. Generalized Abbreviation(Medium)
Write a function to generate the generalized abbreviations of a word.
编写一个函数来生成一个单词的通用缩写。
Example:
Given word = “word”, return the following list (order does not matter):
[“word”, “1ord”, “w1rd”, “wo1d”, “wor1”, “2rd”, “w2d”, “wo2”, “1o1d”, “1or1”, “w1r1”, “1o2”, “2r1”, “3d”, “w3”, “4”]
思路:
使用递归
分两种情况,一种数字,一种字符,数字需要判断,前面是不是数字
def GenerateAbbreviations(word):
def backtracking(word,cur_num,cur_string,is_numberbefore):
if cur_num == len(word):
if is_numberbefore ==0:
res.append(cur_string)
else:
res.append(cur_string+str(is_numberbefore))
else:
if is_numberbefore>0:
backtracking(word,cur_num+1,cur_string+str(is_numberbefore)+word[cur_num],0)
else:
backtracking(word,cur_num+1,cur_string+word[cur_num],0)
backtracking(word,cur_num+1,cur_string,is_numberbefore+1)
res = []
backtracking(word,0,'',0)
return res
(178)93. Restore IP Addresses(Medium)(很少考)
给定仅包含数字的字符串,通过返回所有可能的有效IP地址组合来恢复它。
思路:
1、使用递归,不断的缩小范围
2、当point*3<len(s) 不符合。当len(s)==0 and num_point !=0 不符合
3、当字符大于1的时候,要判断首位不为0,当字符大于2时,要判断数值不可大于255
def dfs(s,num_point,path):
if len(s)==0:
if num_point ==0:
res.append(path[:-1])
return
elif num_point*3 <len(s):
return
dfs(s[1:],num_point-1,path +s[0]+'.')
if 1<len(s) and s[0]!='0':
dfs(s[2:],num_point-1,path+s[:2]+'.')
if 2<len(s) and s[0]!='0':
if int(s[:3])<=255:
dfs(s[3:],num_point-1,path +s[:3]+'.')
else:
return
res =[]
dfs(s,4,'')
return res
(179)282. Expression Add Operators(Hard)
给定一个只包含数字0-9和目标值的字符串,返回所有可能性,在数字之间添加二元运算符(非一元)+, - 或*,以便它们计算目标值。
思路:
1、首先乘法运算符较高,所以需要知道上一个值是什么,用last进行记录
2、可以多个数字连续在一起,但是注意‘00’等不允许出现,因为不是操作数的格式
3、递归的时候总共有4种情况,不添加操作符、+、-、*
def addOperators(self, num, target):
"""
:type num: str
:type target: int
:rtype: List[str]
"""
res, self.target = [], target
for i in range(1,len(num)+1):
if i == 1 or (i > 1 and num[0] != "0"): # prevent "00*" as a number
self.dfs(num[i:], num[:i], int(num[:i]), int(num[:i]), res) # this step put first number in the string
return res
def dfs(self, num, temp, cur, last, res):
if not num:
if cur == self.target:
res.append(temp)
return
for i in range(1, len(num)+1):
val = num[:i]
if i == 1 or (i > 1 and num[0] != "0"): # prevent "00*" as a number
self.dfs(num[i:], temp + "+" + val, cur+int(val), int(val), res)
self.dfs(num[i:], temp + "-" + val, cur-int(val), -int(val), res)
self.dfs(num[i:], temp + "*" + val, cur-last+last*int(val), last*int(val), res)
(180)140. Word Break II(Hard)
给了一个字典,问给定的字符串s能有多少种被字典构造出来的方式,返回每一种构造方式。
思路:
1、使用DFS + DP
2、使用一个字典,记录已经切分过的数组,不必要再次重切
3、接下来使用wordDict来循环,判断是不是
def wordBreak(self, s, wordDict):
"""
:type s: str
:type wordDict: List[str]
:rtype: List[str]
"""
#dfs + dp
# 使用一个数组记住前面已经切分的
res = []
momery = {}
def dfs(s):
if s in momery:
return momery[s]
if s =='':
return ['']
res = []
for word in wordDict:
if s[:len(word)] == word:
for r in dfs(s[len(word):]):
res.append(word +('' if not r else ' '+r))
momery[s] = res
return res
return dfs(s)
(181)351 Android Unlock Patterns
给定Android 3x3密钥锁定屏幕和两个整数m和n,其中1≤m≤n≤9,计算Android锁定屏幕的解锁模式总数,其包括最少m个密钥和最多n个密钥。
Rules for a valid pattern:
- Each pattern must connect at least m keys and at most n keys.
- All the keys must be distinct.
- If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
- The order of keys used matters.
思路:
1、首先记录,哪些两个数字之间有中间键的,建立一个数组
2、使用visited记录已经访问的数字
3、如果有中间键,并且中间键没有被访问,就不进入递归
4、1,3,7,9是对称的,所以我们乘4即可,然后再对数字2调用递归函数,2,4,6,8也是对称的,再乘4,最后单独对5调用一次,然后把所有的加起来就是最终结果了
def numberOfPattern(m,n):
def helper(num,len,ans,visited):
if len >=m:
ans+=1
if len>n:
return ans
visited.append(num)
for next in range(1,10):
if next not in visited:
if num*10+next not in dict or dict[num*10+next] in visited:
ans = helper(next,len,ans,visited)
visited = visited[:-1]
return ans
res = 0
dict[13] = dict[31] = 2
dict[17] = dict[71] = 4
dict[79] = dict[97] = 8
dict[39] = dict[93] = 6
dict[28] = dict[82] = 5
dict[46] = dict[64] = 5
dict[19] = dict[91] = dict[37] = dict[73] = 5
res +=helper(1,1,0,[])*4
res +=helper(2,1,0,[])*4
res +=helper(5,1,0,[])
return res
Dynamic Programming(一维)
(182)70. Climbing Stairs(Easy)
你正在爬楼梯。它需要n步才能达到顶峰。 每次你可以爬1或2步。您可以通过多少不同的方式登顶?
思路:f(1)=1 f(2)=2
1、假如第一次跳一级台阶,剩下还有n-1级台阶,有f(n-1)种跳法
2、假如第一次条2级台阶,剩下n-2级台阶,有f(n-2)种跳法。
f(n)=f(n-1)+f(n-2)
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
if n<=1:
return 1
res = [1,1]
for i in range(n-1):
sum = res[-1]+res[-2]
res.append(sum)
return res[-1]
(183)62. Unique Paths(Medium)
一个人从矩阵的左顶点走到右底点有几种方式
思路:使用dfs方式会超时,使用DP
dp[i][j] = dp[i-1][j] +dp[i][j-1]
dp = [[1 for _ in range(n)] for _ in range(m)]
for i in range(1,m):
for j in range(1,n):
dp[i][j] = dp[i-1][j]+dp[i][j-1]
return dp[-1][-1]
(184)63. Unique Paths II(Medium)
62 题,然后再加上障碍物
思路:首先先用两个循环,横向和竖向走一遍,遇到1,则边0。后一个根据前一个来
然后再用 dp[i][j] = dp[i-1][j] +dp[i][j-1]
if obstacleGrid[0][0] ==1:
return 0
obstacleGrid[0][0] = 1
for i in range(1,len(obstacleGrid)):
if obstacleGrid[i][0]!=0:
obstacleGrid[i][0] =0
else:
obstacleGrid[i][0] = obstacleGrid[i-1][0]
for j in range(1,len(obstacleGrid[0])):
if obstacleGrid[0][j]!=0:
obstacleGrid[0][j] =0
else:
obstacleGrid[0][j] =obstacleGrid[0][j-1]
for i in range(1,len(obstacleGrid)):
for j in range(1,len(obstacleGrid[0])):
if obstacleGrid[i][j] ==0:
obstacleGrid[i][j] = obstacleGrid[i-1][j]+obstacleGrid[i][j-1]
else:
obstacleGrid[i][j] = 0
return obstacleGrid[-1][-1]
(185)64. Minimum Path Sum(Medium)
与63题相似
给定m x n网格填充非负数,找到从左上到右下的路径,最小化了沿其路径的所有数字的总和。
思路相同
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
for i in range(1,len(grid)):
grid[i][0] += grid[i-1][0]
for j in range(1,len(grid[0])):
grid[0][j] +=grid[0][j-1]
for i in range(1,len(grid)):
for j in range(1,len(grid[0])):
grid[i][j] +=min(grid[i-1][j],grid[i][j-1])
return grid[-1][-1]
(186)120. Triangle(Medium)
给定一个三角形,找到从上到下的最小路径总和。您可以移动到下面一行中相邻数字的每一步。
思路:
如果从上到下,需要用到O(n2)的空间
从下到上,我们只需要覆盖上一层就可以了,因为上一层没有用了
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
min_path = triangle[-1]
for layer in range(len(triangle)-2,-1,-1):
for i in range(len(triangle[layer])):
min_path[i] = min(min_path[i+1],min_path[i])+ triangle[layer][i]
return min_path[0]
(187)279. Perfect Squares(Medium)
给定正整数n,找到总和为n的最小正方数(例如,1,4,9,16 …)。
思路:
def numSquares(self, n):
"""
:type n: int
:rtype: int
"""
dp = [i for i in range(n+1)]
for i in range(n+1):
j = 1
while(j*j<=i):
dp[i] = min(dp[i],dp[i -j*j]+1)
j+=1
return dp[n]
(188)139. Word Break(Medium)
给定一个目标字符串和一组字符串,判断目标字符串能否拆分成数个字符串,这些字符串都在给定的那组字符串中。
思路:
1、使用动态规划
2、dp[i] 代表前i个是否满足条件
3、第二层循环是将问题逐步化小
def wordBreak(self, s, wordDict):
"""
:type s: str
:type wordDict: List[str]
:rtype: bool
"""
n,dp = len(s),[True] + [False]*len(s)
for i in range(n):
for j in range(i+1):
if dp[j] and s[j:i+1] in wordDict:
dp[i+1] = True
break
return dp[n]
(189)375. Guess Number Higher or Lower II(Medium)
我们正在玩猜猜游戏。游戏如下: 我从1到n选择一个数字。你必须猜测我选择了哪个号码。 每当你猜错了,我都会告诉你我选的号码是高还是低。但是,当你猜出一个特定的数字x,并且你猜错了,你需支付$ x。当你猜到我选择的数字时,你赢了比赛。
鉴于特定的n≥1,找出您需要多少钱才能保证获胜。
思路:
在1-n个数里面,我们任意猜一个数(设为i),保证获胜所花的钱应该为 i + max(w(1 ,i-1), w(i+1 ,n)),这里w(x,y))表示猜范围在(x,y)的数保证能赢应花的钱,则我们依次遍历 1-n作为猜的数,求出其中的最小值即为答案,即最小的最大值问题
def getMoneyAmount(self, n):
"""
:type n: int
:rtype: int
"""
need = [[0]*(n+1) for _ in range(n+1)]
for low in range(n, 0, -1):
for high in range(low+1, n+1):
need[low][high] = min(x + max(need[low][x-1], need[x+1][high]) for x in range(low, high))
return need[1][n]
(190)312. Burst Balloons(Hard)
给定n个气球,索引从0到n-1。每个气球都涂有一个由数组nums表示的数字。你被要求爆破所有的气球。如果你爆裂气球我会得到nums [left] * nums [i] * nums [right]硬币。这里左边和右边是i的相邻指数。在爆发之后,左右之后变得相邻。 通过明智地爆破气球找到可以收集的最大硬币。
您可以想象nums [-1] = nums [n] = 1.它们不是真实的,因此您不能破坏它们。 0≤n≤500,0≤nums[i]≤100
思路:
气球被分为两个部分,当前气球是最后一个爆裂的,所以可以使用DP进行递归
使用三重循环
第一层循环i,j中间的有多少个元素,从2-n,之所以要从2,是因为i,j中间至少要有一个元素。
第二层循环就是起始点i,从0 到n-gap,此时j = i+gap
第三层循环k,就是哪一个是i到j里面最晚爆炸的。
最后选取结果最大的。
def maxCoins(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
nums = [1] + nums +[1]
n = len(nums)
dp = [[0]*n for _ in xrange(n)]
for gap in xrange(2,n):
for i in range(n-gap):
j = i+gap
for k in range(i+1,j):
dp[i][j] = max(dp[i][j],nums[i]*nums[k]*nums[j] + dp[i][k] +dp[k][j])
return dp[0][n-1]
(191)322. Coin Change(Medium)
您将获得不同面额的硬币和总金额。编写一个函数来计算构成该数量所需的最少数量的硬币。如果这笔钱不能由任何硬币组合弥补,则返回-1。
思路:
会有两个思考:1、coins并不是排好序的 2、有可能有两个相差的金额就是你剩下的钱,所以不能单纯的认为先用最大的,再接着用小额度的。所以循环使用%和/方式不可取
使用dp算法
dp[i] 代表额度为i需要用到的最少数量硬币
所以dp[i] = min(dp[i],dp[i-coins[j]+1)
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
dp = [0] +[float('inf')]*amount
for i in range(1,amount+1):
for c in coins:
if i-c>=0:
dp[i] = min(dp[i],dp[i-c]+1)
return dp[amount] if dp[amount]<float('inf') else -1
Dynamic Programming(二维)
(192)256 Paint House(Easy)
有一排n个房子,每个房子都可以涂上三种颜色中的一种:红色,蓝色或绿色。 用一定颜色绘制每个房子的成本是不同的。 你必须为所有的房屋涂漆,使两个相邻的房屋没有相同的颜色。
用特定颜色绘制每个房屋的成本由n×3成本矩阵表示。 例如,成本[0] [0]是用红色绘制房屋0的成本; 成本[1] [2]是用绿色涂漆房屋1的成本,依此类推…找出所有房屋的最低成本。
Example:
Input: [[17,2,17],[16,16,5],[14,3,19]]
Output: 10
Explanation: Paint house 0 into blue, paint house 1 into green, paint house 2 into blue.
思路:
使用动态规划,使用red,blue,green表示当前位置的最小cost,遍历costs
def minCost(self,costs):
red,blue,green = 0,0,0
for r,b,g in costs:
red,blue,green = min(blue,green)+r,min(red,green)+b,min(red,blue)+green
return min(red,blue,green)
(193)265. Paint House II(Hard)
用特定颜色绘制每个房屋的成本由n×k成本矩阵表示。 例如,成本[0] [0]是用颜色0绘制房屋0的成本; 成本[1] [2]是用颜色2绘制房屋1的成本,依此类推…找出所有房屋的最低成本。 注意:所有费用均为正整数。
Example:
Input: [[1,5,3],[2,9,4]]
Output: 5
Explanation: Paint house 0 into color 0, paint house 1 into color 2. Minimum cost: 1 + 4 = 5;
Or paint house 0 into color 2, paint house 1 into color 0. Minimum cost: 3 + 2 = 5.
Follow up:
Could you solve it in O(nk) runtime?
思路:
正常的dynamic programming思路是填入n * k大小的matrix,而每一个dp[i][j]暴力解的话都需要遍历之前一个房子的O(k)项,这就造成了O(nk^2)的复杂度。follow up中要求O(nk)要怎么做到呢?
实际上我们只需要前一轮至多两个最小值:如果当第 j 个房子和min1一样,那只能选择min2,如果不一样,可以直接选min1。这里的min1和min2应该是index而不是cost,因为我们需要同时知道取到最小cost的上一轮颜色是什么才能选择min1还是min2。
def minCostII(self.costs):
if len(costs) ==0 or len(costs[0]) ==0:
return 0
min_1,min_2,index_1 = 0,0,-1
for i in range(len(costs)):
m1 = float('inf')
m2 = m1
id1 = -1
for j in range(len(cost[i])):
if j == index_1:
cost = costs[i][j] +min_2
else:
cost = cost[i][j] + min_1
if cost<m1:
m2 = m1
m1 = cost
id1 = j
elif cost<m2:
m2 = cost
min_1,min_2,index_1 = m1,m2,id1
return min_1
(194)72. Edit Distance(Hard)
给定两个单词word1和word2,找到将word1转换为word2所需的最小操作数。 您对单词允许以下3个操作:
1、插入一个角色 2、删除一个字符 3、替换一个角色
思路:
1.如果str1的第i个,也就是str1[i-1]和str2的第j个也就是str2[j-1]相等的话,那么 dis[i][j] = dis[i-1][j-1]
2.如果str[i-1] != str2[j-1]
2.1 通过替换操作把str[i-1]替换成str2[j-1],那么
dis[i][j] = dis[i-1][j-1] + 1;
2.2 通过插入操作在str1后面插入str2[j-1], 那么就相当于计算
dis[i][j] = dis[i][j-1] + 1;
2.3 通过插入操作在str2后面插入str1[i-1],那么就是
dis[i][j] = dis[i-1][j] + 1;
在上述三个中选一个最小的。迭代更新。
class Solution(object):
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
dp = [[0 for _ in range(len(word2)+1)] for _ in range(len(word1)+1)]
for i in range(len(word1)+1): dp[i][0] = i
for j in range(len(word2)+1): dp[0][j] = j
for i in range(1,len(word1)+1):
for j in range(1,len(word2)+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1]+1,min(dp[i-1][j]+1,dp[i][j-1]+1))
return dp[-1][-1]
(195)97. Interleaving String(Hard)
给定s1,s2,s3,找出s3是否由s1和s2的交织形成。
思路:(用递归回超时)
字符串的子序列或是匹配问题直接就上动态规划
还可以使用一维dp,不需要两维,因为i依赖于前面的i
1、首先判断横竖的边界条件
for i in range(1,len(s2)+1):
dp[0][i] = True if s2[i-1]==s3[i-1] and dp[0][i-1] else False
for i in range(1,len(s1)+1):
dp[i][0] = True if s1[i-1] == s3[i-1] and dp[i-1][0] else False
2、其次判断i,j
(dp[i-1][j] and s1[i-1]==s3[i-1+j]) or (dp[i][j-1] and s2[j-1]==s3[j-1+i])
# ##上动态规划
def isInterleave(self, s1, s2, s3):
if len(s1)+len(s2)!=len(s3):
return False
dp=[[False for _ in range(len(s2)+1)] for _ in range(len(s1)+1)]
dp[0][0] = True
for i in range(1,len(s2)+1):
dp[0][i] = True if s2[i-1]==s3[i-1] and dp[0][i-1] else False
for i in range(1,len(s1)+1):
dp[i][0] = True if s1[i-1] == s3[i-1] and dp[i-1][0] else False
for i in range(1,len(s1)+1):
for j in range(1,len(s2)+1):
dp[i][j] = True if (dp[i-1][j] and s1[i-1]==s3[i-1+j]) or (dp[i][j-1] and s2[j-1]==s3[j-1+i]) else False
return dp[len(s1)][len(s2)]
(196)174. Dungeon Game(Hard)
皇后右下角,国王从左上角开始寻找皇后,求国王最少需要多少血?
思路:
1、使用dp操作
2、当走完最后一个房间,至少要剩下1格血,最后状态也可以当作最初状态,从最后一个房间往前走,每个房间的血量由下面或者右边一个较小的一个决定:
dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j]
还要考虑每个位置最少最低为一格血
def calculateMinimumHP(self, dungeon):
"""
:type dungeon: List[List[int]]
:rtype: int
"""
m = len(dungeon)
n = len(dungeon[0])
dp = [[2**31-1 for i in range(n+1)] for j in range(m+1)]
dp[m-1][n] = 1
for i in range(m-1,-1,-1):
for j in range(n-1,-1,-1):
dp[i][j] = max(min(dp[i+1][j],dp[i][j+1]) - dungeon[i][j],1)
return dp[0][0]
(197)221. Maximal Square(Medium)
给定填充0和1的2D二进制矩阵,找到仅包含1的最大正方形并返回其面积。
思路:
1、我们初始化dp所有的元素为0
2、dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1. dp就是左边、右边、斜上角最小值+1
3、因为只用到了i-1,所以不需要用到m*n的空间。使用变量存储上一个i-1的值就可以了
def maximalSquare(self, matrix):
"""
:type matrix: List[List[str]]
:rtype: int
"""
if not matrix:
return 0
dp = [0]*(len(matrix[0])+1)
max_ans = 0
pre = 0
for i in range(1,len(matrix)+1):
for j in range(1,len(matrix[0])+1):
temp = dp[j]
if matrix[i-1][j-1] == '1':
dp[j] = min(dp[j],pre,dp[j-1])+1
max_ans = max(max_ans,dp[j])
else:
dp[j] = 0
pre = temp
return max_ans**2
(198)84. Largest Rectangle in Histogram***(Hard)
给定n个非负整数表示直方图的条形高度,其中每个条形的宽度为1,找到直方图中最大矩形的区域。
思路:题型和11题类似,但是解法不同。
此题用stack的思想O(n),重要的几个trick
1、stack = [-1] height.append(0) #在最后面添加一个最小数
2、循环当矩阵不是递增的时候,弹出末尾的元素,然后算面积。否则stack.append(i)(注:是加入索引)
用栈来模拟,遍历heights数组,如果大于栈顶元素,就push进去;否则,持续弹栈来计算从栈顶点到降序点的矩阵大小。然后将这一部分全部替换为降序点的值,即做到了整体依然是有序非降的。
整个过程中,即把所有的局部最大矩阵计算过了,又在宽度范围内保留了全部的场景。
举例,2,1,5,6,3的场景。
先加入一个0,方便最后可以全部弹栈出来。变成:2,1,5,6,3,0.
2进栈,1比栈顶小,对2进行出栈,area = 2;
5,6都是非降的,继续进栈,栈为1,5,6;
遇到3,是一个降序点;开始弹栈,6出栈,对应area=61; 5出栈对应area=52;下一个1比3小,不需要弹栈。然后将5、6的弹栈后的空位压栈为3,这是栈为1,1,3,3,3;
下一步遇到0,开始依次出栈,得到area=31,32,33,14,1*5。
遍历结束。整个过程中max的area为10.
def largestRectangleArea(self, height):
#在最后面添加一个最小数
height.append(0)
stack = [-1]
ans = 0
for i in range(len(height)):
while height[i]<height[stack[-1]]:
h = height[stack.pop()]
w = i - stack[-1] -1
ans = max(ans,h*w)
print(ans)
stack.append(i)
return ans
(199)85. Maximal Rectangle(Hard)
给定填充0和1的2D二进制矩阵,找到仅包含1的最大矩形并返回其区域。
Input:
[
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
Output: 6
思路:横着看,根据每一行的计算,然后使用84题的思路
def maximalRectangle(self, matrix):
"""
:type matrix: List[List[str]]
:rtype: int
"""
if matrix==[] or matrix[0]==[]:
return 0
matrix1 = [0 for _ in range(len(matrix[0])+1)]
max_sum = 0
for i in range(len(matrix)):
for j in range(len(matrix[0])):
if i ==0:
matrix1[j] = int(matrix[i][j])
else:
if matrix[i][j]!='0':
matrix1[j] += 1
else:
matrix1[j] =0
stack = [-1]
for i in range(len(matrix1)):
while matrix1[i]<matrix1[stack[-1]]:
h = matrix1[stack.pop()]
w = i-stack[-1] -1
max_sum = max(max_sum,h*w)
stack.append(i)
return max_sum
(200)363. Max Sum of Rectangle No Larger Than K(Hard)(不会)
给定非空的2D矩阵矩阵和整数k,找到矩阵中矩形的最大和,使得其总和不大于k。
注意: 矩阵内的矩形必须具有> 0的区域。 如果行数远大于列数怎么办?
class Solution(object):
def maxSubArraylessK(self,nums,k):
"""
we need to find the sum[right]-sum[left]<=k
since the bitsect return the index of the sorted value
we can't directly pop the nums[idx]
we should use insort from the bisect
"""
# python set() doesn't support indexing, using list instead
# similar as the c++ or java set()
cumset=[]
cumset.append(0)
maxsum=-1<<32
cursum=0
for i in xrange(len(nums)):
cursum+=nums[i]
# find the lower bound of the index
idx=bisect.bisect_left(cumset,cursum-k)
# find max in sum[right]-sum[left]<=k
if 0<=idx<len(cumset):
maxsum=max(maxsum,cursum-cumset[idx])
# using insort instead of append since bisect_left reason
bisect.insort(cumset,cursum)
return maxsum
def maxSumSubmatrix(self, matrix, k):
"""
:type matrix: List[List[int]]
:type k: int
:rtype: int
"""
"""
The python solution hasn't a good time performance,
since lack some of the datatype to do
I am trying to imitate the way solved in c++ or Java
Ther related quesiton might be:
1. #53. Maximum Subarray
2. Maximum Subarray sum less or equal than K
3. maximun sum of rectangle
"""
if not matrix or not matrix[0]:
return 0
row,col=len(matrix),len(matrix[0])
res=-(1<<32)
# using two pointer to record the scan position
for left in xrange(col):
# reset mem to store the row data
cursums=[0 for _ in xrange(row)]
# since the rectange has area>0
right=left
while right<col:
# count one row
for i in xrange(row):
cursums[i]+=matrix[i][right]
# find the max in this row
curarrmax=self.maxSubArraylessK(cursums,k)
res=max(res,curarrmax)
right+=1
return res
Dynamic Programming(化简)
(201)198. House Robber(Easy)
你是一个专业的强盗,计划在街上抢劫房屋。每个房子都有一定数量的钱存在,阻止你抢劫他们的唯一限制是相邻的房屋有连接的安全系统,如果两个相邻的房子在同一个晚上被打破,它将自动联系警察。
给出一个代表每个房子的金额的非负整数列表,确定今晚可以抢劫的最大金额而不警告警察。
def rob(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
last, now = 0, 0
for i in nums:
last, now = now, max(last + i, now)
return now
(202)213. House Robber II(Medium)
你是一个专业的强盗,计划在街上抢劫房屋。每个房子都藏着一定数量的钱。这个地方的所有房屋都排成一个圆圈。这意味着第一栋房屋是最后一栋房屋的邻居。与此同时,相邻的房屋连接了安全系统,如果两个相邻的房屋在同一个晚上被闯入,它将自动联系警方。
思路:
1、使用DP
2、因为首尾是邻居,所以使用去首,去尾。当作两个数组,然后找出两个数组的最大值
3、比较res[i-1] 和res[i-2]+nums[i]的最大值
4、因为动态数组是k循环的,所以采用k大小的数组,使得空间使用率降为O(1)
def rob(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums) ==0:
return 0
if len(nums)<=3:
return max(nums)
return max(self.rob_row(nums[1:]),self.rob_row(nums[:-1]))
def rob_row(self,nums):
res = [0]*2
res[0] = nums[0]
res[1] = max(nums[0],nums[1])
for i in range(2,len(nums)):
res[i%2] = max(res[(i-1)%2],res[(i-2)%2]+nums[i])
return max(res)
(203)276. Paint Fence
有一个有n个帖子的围栏,每个帖子都可以涂上一种k颜色。 您必须绘制所有帖子,使得不超过两个相邻的栅栏柱具有相同的颜色。 返回可以绘制栅栏的总方式。
思路:
当n=1时, 结果为k
当n = 2时, 分为两种情况, 颜色与上一步相同same, 颜色与上一步不同diff, 此时, same为k, diff为k*(k-1)
当n > 3时, 根据题意, 不能有超过两个颜色相同的篱笆, 那么颜色与上一步相同时的情况只能用上一步的diff推导, 个数为diff. 颜色与上一步不同时, 可以用所有之前的情况, 个数为(same+diff)*(k-1).
def numWays(self, n, k):
if n ==0:
return 0
if n ==k:
return k
same,different = k,k*(k-1)
for i in range(3,n+1):
same,different = different,(same+different)*(k-1)
return same+different
(204)91. Decode Ways(Medium)
Input: “12”
Output: 2
Explanation: It could be decoded as “AB” (1 2) or “L” (12).
思路:
因为dp[i] = dp[i-1] +(dp[i-2] if 0<s[i-1:i+1]<=26)所以只需使用两个变量存储(可覆盖)
一定要注意0不与任何数组成数字的时候,return 0
def numDecodings(self, s):
"""
:type s: str
:rtype: int
"""
#使用dp操作
if len(s)==0 or s[0] =='0':
return 0
dp1 = 1
dp2 = 1
for i in range(1,len(s)):
cur = dp2
#当前面不是0,并且小于26
if int(s[i-1])!=0 and int(s[i-1:i+1])<=26:
cur +=dp1
#如果当前i=0,并且不满足上面的条件。不是合法的
if int(s[i])==0 and cur ==dp2:
return 0
#如果当前i=0,则只能当成一个元素看
elif int(s[i]) ==0:
cur -=dp2
dp1,dp2 = dp2,cur
return dp2
(205)10. Regular Expression Matching(Hard)
给定输入字符串和模式(p),实现与支持 ‘.’ and ‘*’.
‘.’ Matches any single character.
’ * ’ Matches zero or more of the preceding element.
匹配应覆盖整个输入字符串(不是部分)。
Note:
s could be empty and contains only lowercase letters a-z.
p could be empty and contains only lowercase letters a-z, and characters like . or *.
思路:
1, If p.charAt(j) == s.charAt(i) : dp[i][j] = dp[i-1][j-1];
2, If p.charAt(j) == ‘.’ : dp[i][j] = dp[i-1][j-1];
3, If p.charAt(j) == ’ * ':
here are two sub conditions:
1 if p.charAt(j-1) != s.charAt(i) : dp[i][j] = dp[i][j-2] //in this case, a* only counts as empty
2 if p.charAt(j-1) == s.charAt(i) or p.charAt(j-1) == ‘.’:
dp[i][j] = dp[i-1][j] //in this case, a* counts as multiple a
or dp[i][j] = dp[i][j-1] // in this case, a* counts as single a
or dp[i][j] = dp[i][j-2] // in this case, a* counts as empty
def isMatch(self, text, pattern):
"""
:type s: str
:type p: str
:rtype: bool
"""
dp = [[False]*(len(pattern)+1) for _ in range(len(text)+1)]
dp[0][0] = True
for i in range(len(pattern)):
if pattern[i] == '*' and dp[0][i-1]:
dp[0][i+1] = True
for i in range(len(text)):
for j in range(len(pattern)):
if pattern[j] == text[i] or pattern[j] == '.':
dp[i+1][j+1] = dp[i][j]
if pattern[j] == '*':
# in this case, a* counts as empty
if pattern[j-1] != text[i] and pattern[j-1]!='.':
dp[i+1][j+1] = dp[i+1][j-1]
#dp[i+1][j] in this case, a* counts as single a
#dp[i][j+1] in this case, a* counts as multiple a
#dp[i+1][j-1] in this case, a* counts as empty
else:
dp[i+1][j+1] = (dp[i+1][j] or dp[i][j+1] or dp[i+1][j-1])
return dp[-1][-1]
(206)44. Wildcard Matching(Hard)
Given an input string (s) and a pattern §, implement wildcard pattern matching with support for ‘?’ and ‘’.
‘?’ Matches any single character.
'’ Matches any sequence of characters (including the empty sequence).
思路:使用迭代
如果遇到了多个*,只用返回最后一个星。还要记录star的位置和s当前位置
1、使用两个变量分别记录最后一个星的位置和当时s的位置
2、四个条件:如果一对一匹配,都加一;如果p为*,记录;如果无法匹配且前面有*,P重来,S加一;如果都不匹配,False
3、如果j结束了,P后面应该都要*
def isMatch(self, s, p):
"""
:type s: str
:type p: str
:rtype: bool
"""
i =0
j =0
jIndex = -1
starIndex = -1
while(j<len(s)):
##一对一匹配,都加一
if (i<len(p) and (s[j]==p[i] or p[i]=='?')):
i+=1
j+=1
## p为*,记录下p和s的索引。P到下一个位置
elif (i<len(p) and (p[i]=='*')):
jIndex = j
starIndex = i
i+=1
## 如果不匹配,则判断前面是不是有*,同时jIndex前进一步,P则重新来
elif (starIndex!=-1):
j = jIndex+1
i = starIndex+1
jIndex +=1
##如果都不对,返回False
else:
return False
## j如果结束了,p没结束,p必须后面都是*
while(i<len(p)and p[i]=='*'):
i+=1
return i==len(p)
LinkedList(基础)
(207)206. Reverse Linked List(Easy)
反转单链表
Input: 1->2->3->4->5->NULL
Output: 5->4->3->2->1->NULL
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
prev = None
curr = head
while curr:
next = curr.next
curr.next = prev
prev = curr
curr = next
return prev
(208)141. Linked List Cycle(Easy)
给定一个链表,确定它是否有一个循环。
为了表示给定链表中的循环,我们使用整数pos来表示tail连接到的链表中的位置(0索引)。如果pos为-1,则链表中没有循环。
思路:
使用快慢指针
def hasCycle(self,head):
"""
:type head: ListNode
:rtype: bool
"""
if head ==None or head.next ==None:
return False
slow = head
fast = head.next
while slow!=fast:
if fast ==None or fast.next ==None:
return False
slow = slow.next
fast = fast.next.next
return True
(209)142. Linked List Cycle II(Medium)
给定链表,返回循环开始的节点。如果没有循环,则返回null。
思路:
第一次相遇时slow走过的距离:a+b,fast走过的距离:a+b+c+b。
因为fast的速度是slow的两倍,所以fast走的距离是slow的两倍,有 2(a+b) = a+b+c+b,
可以得到a=c(这个结论很重要!)。
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def detectCycle(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
first = head
second = head
while first and second:
first = first.next
if second.next:
second =second.next.next
else:
return None
if first ==second:
first = head
while first != second:
first = first.next
second = second.next
return first
return None
(210)143. Reorder List(Medium)
思路:
1、先找出中间的node
2、将中间后面的给反转
3、然后两个链表相连
def reorderList(self, head):
"""
:type head: ListNode
:rtype: None Do not return anything, modify head in-place instead.
"""
if head ==None:
return head
first,second = head,head
##找出中间的
while second.next and second.next.next:
first = first.next
second = second.next.next
cur = first.next
node = first.next = None
## 反转后面的
while cur:
next = cur.next
cur.next = node
node = cur
cur = next
##交替相连
cur1 = head
cur2 = node
while cur2:
next = cur1.next
cur1.next = cur2
next2 = cur2.next
cur2.next = next
cur2 = next2
cur1 = next
(211)24. Swap Nodes in Pairs(Medium)
给定链表,交换每两个相邻节点并返回其头部。 您可能无法修改列表节点中的值,只能更改节点本身。
思路:
主要是搞清楚交换的点
def swapPairs(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
pre,pre.next = self,head
cur = pre
while cur.next!=None and cur.next.next !=None:
a = cur.next
b = a.next
cur.next, b.next, a.next = b, a, b.next
cur = a
return pre.next
(212)328. Odd Even Linked List(Medium)
给定单链表,将所有奇数节点组合在一起,然后是偶数节点。请注意,这里我们讨论的是节点编号,而不是节点中的值。
你应该尝试到位。该程序应该以O(1)空间复杂度和O(节点)时间复杂度运行。
注意: 偶数组和奇数组内的相对顺序应保持与输入中的相对顺序。 第一个节点被认为是奇数,第二个节点被认为是偶数等等…
思路:
使用oddhead,和evenhead,最后将两个相连。要记录evenhead的第一个元素
def oddEvenList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if head == None:
return None
odd,even,evenhead = head,head.next,head.next
while even and even.next:
odd.next = even.next
even.next = even.next.next
even = even.next
odd = odd.next
odd.next = evenhead
return head
(213)92. Reverse Linked List II(Medium)
Reverse a linked list from position m to n. Do it in one-pass.
Input: 1->2->3->4->5->NULL, m = 2, n = 4
Output: 1->4->3->2->5->NULL
思路:先把m给找到,然后从m开始到n先调转,然后再头尾对应的连上
def reverseBetween(self, head, m, n):
"""
:type head: ListNode
:type m: int
:type n: int
:rtype: ListNode
"""
if m ==n:
return head
pre = ListNode(0)
pre.next = head
cur = pre
i = 1
while i<m:
cur = cur.next
i+=1
#使用m_cur记住reversed的前面一个
m_cur = cur
cur = cur.next
Reversed = None
#要reverse的自己内部先转,然后再与外部链接
while i<=n:
next = cur.next
cur.next = Reversed
Reversed = cur
cur = next
i+=1
m_cur.next.next = cur
m_cur.next = Reversed
return pre.next
(214)237. Delete Node in a Linked List(Easy)
编写一个函数来删除单链表中的节点(尾部除外),只允许访问该节点。
The linked list will have at least two elements.
All of the nodes’ values will be unique.
The given node will not be the tail and it will always be a valid node of the linked list.
Do not return anything from your function.
思路:
给的输入是当前这个节点,不是头结点
将下一个节点的值赋给当前节点
next指向next.next
def deleteNode(self, node):
"""
:type node: ListNode
:rtype: void Do not return anything, modify node in-place instead.
"""
node.val = node.next.val
node.next = node.next.next
(215)19. Remove Nth Node From End of List
给定链接列表,从列表末尾删除第n个节点并返回其头部。
思路:
1、定义两个指针,相隔n个
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
pre = head
cur = head
for i in range(n):
cur = cur.next
if cur==None:
return head.next
while cur.next!=None:
cur = cur.next
pre = pre.next
pre.next = pre.next.next
return head
(216)83. Remove Duplicates from Sorted List(Easy)
Given a sorted linked list, delete all duplicates such that each element appear only once.
def deleteDuplicates(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if head ==None:
return head
cur = head
while cur.next !=None:
if cur.val == cur.next.val:
cur.next = cur.next.next
else:
cur = cur.next
return head
(217)203. Remove Linked List Elements(Easy)
从具有值val的整数的链接列表中删除所有元素。
Input: 1->2->6->3->4->5->6, val = 6
Output: 1->2->3->4->5
思路:
使用迭代,遇到相同的就跳过,记得很多坑
def removeElements(self, head, val):
"""
:type head: ListNode
:type val: int
:rtype: ListNode
"""
pre,pre.next = self,head
cur = pre
while cur:
if cur.next and cur.next.val ==val:
cur.next = cur.next.next
else:
cur = cur.next
return pre.next
(218)82. Remove Duplicates from Sorted List II(Medium)
给定已排序的链接列表,删除所有具有重复数字的节点,只留下原始列表中的不同数字。
def deleteDuplicates(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
pre,pre.next = self,head
cur = pre
while cur.next and cur.next.next:
if cur.next.val == cur.next.next.val:
#防止出现奇数个相同的数字,并且确保next.next不为空。
#最后要删掉cur.next
while cur.next.next and cur.next.val == cur.next.next.val:
cur.next.next = cur.next.next.next
cur.next = cur.next.next
else:
cur = cur.next
return pre.next
(219)369 Plus One Linked List(Medium)
给定一个非负数表示为单个链接的数字列表,加上一个数字。 存储数字使得最高有效数字位于列表的开头。
Example:
Input:
1->2->3
Output:
1->2->4
思路:
首先先要把链表进行翻转,然后进行加一操作,记得要进位,最后要判断要不要加节点。最后再把链表翻转
def plusOne(self,head):
(220)2. Add Two Numbers(Medium)
给你两个表示两个非负数字的链表。数字以相反的顺序存储,其节点包含单个数字。将这两个数字相加并将其作为一个链表返回。
输入: (2 -> 4 -> 3) + (5 -> 6 -> 4)
输出: 7 -> 0 -> 8
思路:
1.进位问题
2. l1 和 l2 长度不同
3. .当 l1 + l2 大于1000 进位问题.
def addTwoNumbers(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
add = 0
head = ListNode(0)
point = head
while l1 !=None and l2!=None:
point.next = ListNode((l1.val+l2.val+add)%10)
add = (l1.val+l2.val+add)/10
l1 = l1.next
l2 = l2.next
point = point.next
while l1!=None:
point.next = ListNode((l1.val+add)%10)
add = (l1.val+add)/10
l1 = l1.next
point = point.next
while l2!=None:
point.next = ListNode((l2.val+add)%10)
add = (l2.val+add)/10
l2 = l2.next
point = point.next
if add>0:
point.next = ListNode(add)
return head.next
(221)160
(222)21. Merge Two Sorted Lists(Easy)
合并两个已排序的链接列表并将其作为新列表返回。新列表应该通过拼接前两个列表的节点来完成。
思路:
1、就是合并排序的merge的实现
def mergeTwoLists(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
head = ListNode(0)
cur = head
while l1!=None and l2!=None:
if l1.val>l2.val:
cur.next = l2
l2 = l2.next
else:
cur.next = l1
l1 = l1.next
cur = cur.next
while l1!=None:
cur.next = l1
l1 = l1.next
cur = cur.next
while l2!=None:
cur.next = l2
l2 = l2.next
cur= cur.next
return head.next
LinkedList(提高)
(223)234. Palindrome Linked List(Easy)
给出一个单链表,确定它是否是回文。
你能在O(n)时间和O(1)空间做吗?
思路:
先使用快慢指针,找到中间的节点(奇数,偶数没关系)只要后面的长度比较短就可以了
然后反转后面的链表
最后比较两个链表
由于有三个指针交换,把next放在前面就没问题
def isPalindrome(self, head):
"""
:type head: ListNode
:rtype: bool
"""
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
reverse = None
while slow:
slow.next,slow,reverse = reverse,slow.next,slow
while reverse:
if reverse.val!=head.val:
return False
reverse = reverse.next
head = head.next
return True
(224)148. Sort List(Medium)
使用常量空间复杂度在O(n log n)时间内对链表进行排序。
思路:
满足这样要求的排序算法,我们首先想到快排,合并排序和堆排序。
快排的最坏的时间复杂度是O(n^2),平均复杂度为O(nlgn)
堆排序实现上过于繁琐,我们不做考虑
使用归并
1、首先要将链表一步一步缩小(使用递归)定义三个变量,pre、slow、fast
2、其次使用归并操作
def sortList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if head==None or head.next==None:
return head
pre = slow = fast = head
while fast!=None and fast.next!=None:
pre = slow
slow = slow.next
fast = fast.next.next
pre.next = None
i = self.sortList(head)
j = self.sortList(slow)
return self.merge(i,j)
def merge(self,i,j):
cur = tempNode = ListNode(0)
while i!=None or j!=None:
if i == None:
cur.next = j
j = j.next
elif j ==None:
cur.next = i
i = i.next
elif i.val>j.val:
cur.next = j
j = j.next
else:
cur.next = i
i = i.next
cur = cur.next
return tempNode.next
(225)25. Reverse Nodes in k-Group(Hard)
给定链表,一次反转链表k的节点并返回其修改后的列表。
k是正整数,并且小于或等于链表的长度。如果节点数不是k的倍数,那么最后的剩余节点应该保持不变。
Example:
Given this linked list: 1->2->3->4->5
For k = 2, you should return: 2->1->4->3->5
For k = 3, you should return: 3->2->1->4->5
思路:
1、使用左右指针,然后对结果进行交换
2、还需要一个指针用来记录当前节点的前一个
2、下次要注意,如果是三个交换,记得把next写在前面
def reverseKGroup(self, head, k):
"""
:type head: ListNode
:type k: int
:rtype: ListNode
"""
pre,pre.next = ListNode(0),head
l = r = head
next_head = pre
while True:
count = 0
while r and count<k:
r = r.next
count +=1
if count == k:
temp,cur = r,l
for _ in range(k):
#这里是三个元素,所以要有次序,在这里搞了很久,次序影响结果(仍然没搞明白,最好使用赋值的方法),下次把next放在前面,并且数组a,b反过来也不行
cur.next,temp,cur = temp,cur,cur.next
#这里也一样
next_head.next,next_head,l = temp,l,r
else:
return pre.next
(226)61. Rotate List(Medium)
给定链表,将列表向右旋转k个位置,其中k为非负数。
Input: 1->2->3->4->5->NULL, k = 2
Output: 4->5->1->2->3->NULL 右移k位
思路:先找出有多少个,趁前面不注意,然后一次将后面几个移到前面。
def rotateRight(self, head, k):
"""
:type head: ListNode
:type k: int
:rtype: ListNode
"""
start = head
end = head
if end ==None or end.next ==None:
return head
i=1
while(end.next!=None):
i+=1
end = end.next
##免得走多了一个轮回
k%=i
for j in range(i-k-1):
start = start.next
end.next = head
head = start.next
start.next = None
return head
(227)86. Partition List(Medium)
给一个链表,将小于值x的结点放到所有大于等于值x的结点的前面,不要改变结点之间的顺序(例如1,4,3,2,5,2 将2结点提到至4的前面,但4,3,5的顺序不变);
思路:设置一个变量,记录下链表中第一次出现大于等于值x结点的位置insertPos。之后遍历链表,将所有小于值x的结点提到这个位置上
(好像还有更好的解法)
def partition(self, head, x):
"""
:type head: ListNode
:type x: int
:rtype: ListNode
"""
pre = ListNode(0)
pre.next = head
start = pre
while start.next != None:
if start.next.val >=x:
break
start = start.next
cur = start
while cur.next !=None:
if cur.next.val < x:
print(cur.val,cur.next.val,start.val,start.next.val)
cur.next,start.next,start.next.next = cur.next.next,cur.next,start.next
start = start.next
# print(cur.val,cur.next.val,start.val,start.next.val)
else:
cur = cur.next
if cur ==None:
break
return pre.next
(228)23. Merge k Sorted Lists(Hard)
合并k个已排序的链表并将其作为一个排序列表返回。分析并描述其复杂性。
思路:
1、将list中的每个元素的值存入list中
2、将list进行排序,然后建立node,加入next
from Queue import PriorityQueue
class Solution(object):
def mergeKLists(self, lists):
"""
:type lists: List[ListNode]
:rtype: ListNode
"""
queue = PriorityQueue()
head = ListNode(0)
cur = head
for i in lists:
if i:
queue.put((i.val,i))
while queue.qsize()>0:
cur.next = queue.get()[1]
cur = cur.next
if cur.next:
queue.put((cur.next.val,cur.next))
return head.next
(229)147. Insertion Sort List(Medium)
使用插入排序对链接列表进行排序。
思路:
定义一个辅助链表头
然后循环找到合适的位置插入
def insertionSortList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if head == None:
return None
pre=temp= ListNode(0)
cur = head
next = None
while cur:
while (pre.next!=None and cur.val>pre.next.val):
pre = pre.next
next = cur.next
cur.next = pre.next
pre.next = cur
cur = next
pre = temp
return pre.next
Binary Search(基础)
(230)278. First Bad Version(Easy)
您是产品经理,目前领导团队开发新产品。不幸的是,您产品的最新版本未通过质量检查。
由于每个版本都是基于以前的版本开发的,因此糟糕版本之后的所有版本也都很糟糕。
假设您有n版本,[1, 2, …, n]并且您想找出第一个坏版本,这会导致以下所有版本都不好。
您将获得一个API bool isBadVersion(version),它将返回是否version为坏。实现一个函数来查找第一个坏版本。您应该最小化对API的调用次数。
思路:
使用二分法,考虑边界条件 right不加1
def firstBadVersion(self, n):
"""
:type n: int
:rtype: int
"""
left,right = 1,n
while left<right:
middle = (left+right)//2
if isBadVersion(middle):
right = middle
else:
left = middle+1
return left
(231)35. Search Insert Position(Easy)
给定排序数组和目标值,如果找到目标,则返回索引。如果没有,请返回索引按顺序插入的索引。 您可以假设数组中没有重复项。
思路:
1、使用二分法
2、当end-start <=1时退出
3、 当target<=start,return start
elif 当target>end, return end +1
else 当target<=end ,return end
def searchInsert(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
start = 0
end = len(nums)-1
while(end-start >1):
middle = int((start+end)/2)
if nums[middle]>target:
end = middle
elif nums[middle]==target:
return middle
else:
start = middle
if target<=nums[start]:
return start
elif target>nums[end]:
return end+1
else:
return end
(232)33. Search in Rotated Sorted Array(Medium)
按升序排序的数组在事先未知的某个枢轴处旋转。 (即[0,1,2,4,5,6,7]可能变为[4,5,6,7,0,1,2])。
您将获得要搜索的目标值。如果在数组中找到则返回其索引,否则返回-1。
思路:使用二分法,如果中间的点比右边的点小,说明右边时有序的,否则左边时有序的
然后分右边有序和左边有序两种情况进行讨论。
def search(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
l = 0
r = len(nums)-1
while(l<=r):
middle = int((l+r)/2)
print(middle)
if nums[middle]==target:
return middle
# mean right is in order
if nums[middle]<nums[r]:
if target>nums[middle] and target<=nums[r]:
l = middle+1
else:
r = middle-1
print(l,r)
else:
if target<nums[middle] and target>=nums[l]:
r = middle -1
else:
l = middle +1
return -1
(233)81. Search in Rotated Sorted Array II
假设按升序排序的数组在事先未知的某个枢轴处旋转。 (即[0,0,1,2,2,5,6]可能成为[2,5,6,0,0,1,2])。
相较于Ⅰ,多了重复元素。
思路:程序差不多,只不过多了一个判断,当l ==l+1,l +=1
当middle<right 说明右边是有序的
def search(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: bool
"""
l = 0
r = len(nums)-1
while(l<=r):
while(l<r and nums[l] == nums[l+1]):
l +=1
middle = (l+r)/2
if nums[middle] == target:
return True
if nums[middle]<=nums[r]:
if nums[middle]<target and target<=nums[r]:
l = middle +1
else:
r = middle -1
else:
if nums[middle]>target and target>=nums[l]:
r = middle -1
else:
l = middle +1
return False
(234)153. Find Minimum in Rotated Sorted Array(Medium)
假设按升序排序的数组在事先未知的某个枢轴处旋转。找出最小值
思路:
使用二分法查找
def findMin(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
start = 0
end = len(nums)-1
while end-start>1:
middle = int((start+end)/2)
if nums[middle]>nums[end]:
start = middle
else:
end = middle
return nums[start] if nums[start]<nums[end] else nums[end]
(235)154. Find Minimum in Rotated Sorted Array II(Hard)
假设按升序排序的数组在事先未知的某个枢轴处旋转。找到最小元素。 该数组可能包含重复项。
思路:
遇到左边重复的就加一
def findMin(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
left,right = 0,len(nums)-1
while right - left >1:
if nums[left] ==nums[left+1]:
left +=1
else:
middle = (left+right)//2
if nums[middle]>nums[right]:
left = middle
else:
right = middle
return nums[left] if nums[left]<nums[right] else nums[right]
(236)162. Find Peak Element(Medium)
峰值元素是大于其邻居的元素。
思路:
思路一(O(n))
首先要么单调递增、要么单调递减、要么上升之后减。
所以当出现开始下降的时候,该index就是了,不需要考虑之前的
def findPeakElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(len(nums)-1):
if nums[i]>nums[i+1]:
return i
return len(nums)-1
思路二(O(logn))
def findPeakElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
left,right = 0,len(nums)-1
while left<right:
middle = (left+right)//2
if nums[middle]<nums[middle+1]:
left = middle+1
else:
right = middle
return left
(237) 374 Guess Number Higher or Lower(EASY)
我们正在玩猜猜游戏。游戏如下:
我从1到n选择一个数字。你必须猜测我选择了哪个号码。
每当你猜错了,我都会告诉你这个数字是高还是低。
调用一个预先定义的API guess(int num)返回3个可能的结果(-1,1,或0):
-1:我的号码较低
1:我的号码更高
0:恭喜!你说对了!
def guessNumber(self, n):
"""
:type n: int
:rtype: int
"""
start = 1
end = n
if guess(n)==0:
return n
if guess(1)==0:
return 1
while end - start >1:
middle = int((start+end)/2)
if guess(middle)==-1:
end = middle
elif guess(middle)==1:
start = middle
else:
return middle
(238)34. Find First and Last Position of Element in Sorted Array(Medium)
Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.
Your algorithm’s runtime complexity must be in the order of O(log n).
If the target is not found in the array, return [-1, -1].
思路:
1、使用二分法
2、判断边界
def searchRange(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
low = 0
high = len(nums)-1
if high <0 or target<nums[low] or target>nums[high]:
return [-1,-1]
while(low<=high):
middle = int((low+high)/2)
if nums[middle]>target:
high = middle-1
elif nums[middle]<target:
low = middle+1
else:
low = high = middle
while(low>0 and nums[low-1]==target):
low -=1
while(high<len(nums)-1 and nums[high+1]==target):
high +=1
break
if nums[low]==target:
return [low,high]
else:
return [-1,-1]
(239)349. Intersection of Two Arrays(Easy)
给定两个数组,编写一个函数来计算它们的交集。
def intersection(self, nums1: 'List[int]', nums2: 'List[int]') -> 'List[int]':
nums1=set(nums1)
nums2=set(nums2)
return list(nums1&nums2)
(240)349. Intersection of Two Arrays(Easy)
给定两个数组,编写一个函数来计算它们的交集。可以有重复
思路:
可以使用字典来做
也可以先排序,然后使用判断来做
i=0
j=0
nums1,nums2 = sorted(nums1),sorted(nums2)
res = []
while i<len(nums1) and j<len(nums2):
if nums1[i]>nums2[j]:
j+=1
elif nums1[i]<nums2[j]:
i+=1
else:
res.append(nums1[i])
i +=1
j +=1
return res
def intersect(self, nums1, nums2):
counts = {}
res = []
for num in nums1:
counts[num] = counts.get(num, 0) + 1
for num in nums2:
if num in counts and counts[num] > 0:
res.append(num)
counts[num] -= 1
return res
(241)315. Count of Smaller Numbers After Self(Hard)
您将获得一个整数数组nums,您必须返回一个新的计数数组。 counts数组具有其中count [i]是nums [i]右边的较小元素的数量的属性。
(242)315. Count of Smaller Numbers After Self(Hard)
您将获得一个整数数组nums,您必须返回一个新的计数数组。 counts数组具有其中count [i]是nums [i]右边的较小元素的数量的属性。
思路:
使用归并算法的思想(不太懂)
def countSmaller(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
def sort(enum):
half = len(enum) / 2
if half:
left, right = sort(enum[:half]), sort(enum[half:])
for i in range(len(enum))[::-1]:
if not right or left and left[-1][1] > right[-1][1]:
smaller[left[-1][0]] += len(right)
enum[i] = left.pop()
else:
enum[i] = right.pop()
return enum
smaller = [0] * len(nums)
sort(list(enumerate(nums))) #[(0, 5), (1, 2), (2, 6), (3, 1)])
return smaller
(243)300. Longest Increasing Subsequence(Medium)
给定未排序的整数数组,找到最长的增加子序列的长度。
可能有多个LIS组合,只需要您返回长度。 您的算法应该以O(n2)复杂度运行。
你能把它提高到O(n log n)的时间复杂度吗?
思路:
## 思路一O(n2)
##如果当前nums[i]>nums[j] 那么dp[i]就等于dp[j]中最大的+1
## 思路二 O(nlogn)
##1. 将第1个数字加入解集
##2. 依次读取后面的数字,如果此数字比解集中最后一个数字大,则将此数字追加到解集后
##3. 否则,用这个数字替换解集中第一个比此数字大的数,因为解集是有序的,所以可以使用二分法
##例子:
##举个栗子,输入为[1,4,6,2,3,5]:
##-解集初始化为[1];
##-读到4,将其追加到解集中,解集变为[1,4];
# -读到6,将其追加到解集中,解集变为[1,4,6];
# -读到2,用其替换解集中的4,解集变为[1,2,6],注意此时解集不是一个合法解,因为2是在6后出现的,但是解集的长度始终标识着当前最长序列的长度;
# -读到3,用其替换解集中的6,解集变为[1,2,3];
# -读到5,将其追加到解集中,解集变为[1,2,3,5],得到答案为解集长度4。
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
## 思路一O(n2)
##如果当前nums[i]>nums[j] 那么dp[i]就等于dp[j]中最大的+1
# n = len(nums)
# if n ==0:
# return 0
# dp = [0]*n
# dp[0] =1
# for i in range(n):
# cur_max = 0
# for j in range(0,i):
# if nums[i]>nums[j]:
# cur_max = max(cur_max,dp[j])
# dp[i] = cur_max + 1
# return max(dp)
## 思路二 O(nlogn)
##1. 将第1个数字加入解集
##2. 依次读取后面的数字,如果此数字比解集中最后一个数字大,则将此数字追加到解集后
##3. 否则,用这个数字替换解集中第一个比此数字大的数,因为解集是有序的,所以可以使用二分法
##例子:
##举个栗子,输入为[1,4,6,2,3,5]:
##-解集初始化为[1];
##-读到4,将其追加到解集中,解集变为[1,4];
# -读到6,将其追加到解集中,解集变为[1,4,6];
# -读到2,用其替换解集中的4,解集变为[1,2,6],注意此时解集不是一个合法解,因为2是在6后出现的,但是解集的长度始终标识着当前最长序列的长度;
# -读到3,用其替换解集中的6,解集变为[1,2,3];
# -读到5,将其追加到解集中,解集变为[1,2,3,5],得到答案为解集长度4。
n = len(nums)
if n ==0:
return 0
res = [nums[0]]
for i in range(1,n):
if nums[i]>res[-1]:
res.append(nums[i])
else:
index = self.midSearch(res,nums[i])
res[index] = nums[i]
return len(res)
def midSearch(self,res,val):
p = 0
q = len(res)-1
while(p<=q):
m = (p+q)//2
if res[m] ==val:
return m
if res[m] >val:
q = m -1
else:
p = m + 1
return p
(244)354. Russian Doll Envelopes(Hard)
你有许多宽度和高度的信封,它们是一对整数(w,h)。当且仅当一个信封的宽度和高度都大于另一个信封的宽度和高度时,一个信封可以装入另一个信封。
俄罗斯娃娃的最大信封数量是多少? (把一个放在另一个里面)
不允许轮换。
def maxEnvelopes(self, envelopes):
"""
:type envelopes: List[List[int]]
:rtype: int
"""
res = []
def compare(x,y):
if x[0]==y[0]:
if x[1]>y[1]:
return -1
else:
return 1
else:
if x[0]<y[0]:
return -1
else:
return 1
envelopes.sort(cmp = compare)
for i in envelopes:
if not res or i[1]>res[-1]:
res.append(i[1])
else:
left =0
right = len(res)-1
while left<=right:
mid = (left+right)//2
if res[mid]<i[1]:
left = mid +1
else:
right = mid-1
res[left] = i[1]
return len(res)
Matrix
(245)48. Rotate Image(Medium)
旋转 n*n 矩阵
Rotate the image by 90 degrees (clockwise).
思路:沿着副对角线对折,然后沿着中线对折 or 沿着中线对折,然后沿着对角线对折
matrix[i][j],matrix[n-j-1][n-i-1] = matrix[n-j-1][n-i-1],matrix[i][j]
n = len(matrix[0])
#沿着副对角线对折
for i in range(len(matrix)):
for j in range(len(matrix)-i-1):
matrix[i][j],matrix[n-j-1][n-i-1] = matrix[n-j-1][n-i-1],matrix[i][j]
#沿着水平线对折
for i in range(len(matrix)/2):
for j in range(len(matrix[0])):
matrix[i][j],matrix[n-i-1][j] = matrix[n-i-1][j],matrix[i][j]
(246)54. Spiral Matrix(Medium)
给一个矩阵,输出其螺旋结果
定义rowBegin,rowEnd ,colBegin,colEnd
然后循环.
注意: 当往上走的时候,和往左走的时候,记得判断该行或该列符不符合要求(即判断rowB<=rowE or colB<=colE)
def spiralOrder(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: List[int]
"""
if len(matrix)==0:
return []
rowB =0
rowE = len(matrix)-1
colB = 0
colE = len(matrix[0])-1
res =[]
while(rowB<=rowE and colB<=colE):
#right
for i in range(colB,colE+1):
res.append(matrix[rowB][i])
rowB +=1
#down
for i in range(rowB,rowE+1):
res.append(matrix[i][colE])
colE -=1
if rowB<=rowE:
#left
for i in range(colE,colB-1,-1):
res.append(matrix[rowE][i])
rowE -=1
#up
if colB<=colE:
for i in range(rowE,rowB-1,-1):
res.append(matrix[i][colB])
colB +=1
return res
(247)59. Spiral Matrix II(Medium)
给定正整数n,以螺旋顺序生成填充有从1到n2的元素的方阵。
Input: 3
Output: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
思路:和前面的题类似,用上下左右四个指针
def generateMatrix(self, n):
"""
:type n: int
:rtype: List[List[int]]
"""
res = [[0 for _ in range(n)] for i in range(n)]
left =0
right=n-1
down =n-1
up =0
#left
j =1
while(left<=right and up<=down):
#left
for i in range(left,right+1):
res[up][i] = j
j +=1
up +=1
#down
for i in range(up,down+1):
res[i][right] = j
j+=1
right -=1
#right
for i in range(right,left-1,-1):
res[down][i] = j
j +=1
down -=1
#up
for i in range(down,up-1,-1):
res[i][left] = j
j+=1
left +=1
return res
(248)73. Set Matrix Zeroes
给定m×n矩阵,如果元素为0,则将其整个行和列设置为0.就地执行。
思路:
#不需要空间的做法
#首先判断第一行和第一列有没有0,用bool保存
#利用第一行和第一列来存储
def setZeroes(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: None Do not return anything, modify matrix in-place instead.
"""
#不需要空间的做法
#首先判断第一行和第一列有没有0,用bool保存
#利用第一行和第一列来存储
first_row = False
first_col = False
for i in range(len(matrix)):
if matrix[i][0]==0:
first_row = True
for j in range(len(matrix[0])):
if matrix[0][j]==0:
first_col = True
for i in range(1,len(matrix)):
for j in range(1,len(matrix[0])):
if matrix[i][j] ==0:
matrix[0][j] = matrix[i][0] = 0
for i in range(1,len(matrix)):
for j in range(1,len(matrix[0])):
if matrix[0][j]==0 or matrix[i][0] ==0:
matrix[i][j] =0
if first_row:
for i in range(len(matrix)):
matrix[i][0] =0
if first_col:
for j in range(len(matrix[0])):
matrix[0][j] =0
(249)311 Sparse Matrix Multiplication(Medium)
给定两个稀疏矩阵A和B,返回AB的结果。 您可以假设A的列号等于B的行号。
思路:
一个 i x k 的矩阵A乘以一个 k x j 的矩阵B会得到一个 i x j 大小的矩阵C,矩阵中的某个元素
C[i][j]=A[i][0]*B[0][j] + A[i][1]*B[1][j] + … + A[i][k]*B[k][j],
为了不重复计算0乘0,遍历A, B数组, 如果A[i][k], B[K][J]不为0,才继续计算,累加结果
res[i][j] += A[i][k] * B[k][j]。
def multiply(self,A,B):
"""
:type A: List[List[int]]
:type B: List[List[int]]
:rtype: List[List[int]]
"""
res = [[0]*len(B[0]) for _ in range(len(A))]
for i in range(len(A)):
for k in range(len(A[0])):
if A[i][k]:
for j in range(len(B[0])):
res[i][j] += A[i][k] *B[k][j]
return res
(250)329. Longest Increasing Path in a Matrix(Hard)
给定整数矩阵,找到最长增加路径的长度。 从每个单元格,您可以移动到四个方向:左,右,上或下。您可能不会沿对角线移动或移动到边界之外(即不允许环绕)。
思路:
为每个元素使用dfs,并且使用dp存储最大路径
def longestIncreasingPath(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: int
"""
def dfs(i,j):
#判断时候访问过,访问过就跳过
if not dp[i][j]:
val = matrix[i][j]
dp[i][j] = 1 + max(
dfs(i-1,j) if i and val>matrix[i-1][j] else 0,
dfs(i,j-1) if j and val>matrix[i][j-1] else 0,
dfs(i+1,j) if i<row-1 and val>matrix[i+1][j] else 0,
dfs(i,j+1) if j<col-1 and val>matrix[i][j+1] else 0
)
return dp[i][j]
if not matrix or not matrix[0]:
return 0
row,col = len(matrix),len(matrix[0])
dp = [[0]*col for _ in range(row)]
return max(dfs(x,y) for x in range(row) for y in range(col))
(251)378. Kth Smallest Element in a Sorted Matrix(Medium)
给定n×n矩阵,其中每个行和列按升序排序,找到矩阵中的第k个最小元素。 请注意,它是排序顺序中的第k个最小元素,而不是第k个不同元素。
思路:
使用堆来操作
heapq.heappush()函数把值加入堆中
heapq.heappop() 函数弹出堆中最小值
def kthSmallest(self, matrix, k):
"""
:type matrix: List[List[int]]
:type k: int
:rtype: int
"""
result, heap,n = None, [],len(matrix)
heapq.heappush(heap, (matrix[0][0], 0, 0))
while k > 0:
result, i, j = heapq.heappop(heap)
#除了第一行需要加入,其他行通过列也加入了。
if i == 0 and j + 1 < n:
heapq.heappush(heap, (matrix[i][j + 1], i, j + 1))
if i + 1 < n:
heapq.heappush(heap, (matrix[i + 1][j], i + 1, j))
k -= 1
return result
(252)74. Search a 2D Matrix(Medium)
编写一个有效的算法,搜索sorted m×n矩阵中的值。
每行中的整数从左到右排序。 每行的第一个整数大于前一行的最后一个整数。
先找到值再哪一行,然后再用中值查询
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
i =0
if matrix ==[] or matrix[0]==[]:
return False
while(i<len(matrix)):
if matrix[i][-1]<target:
i+=1
continue
elif matrix[i][-1]>target:
left = 0
right = len(matrix[i])-1
while left<=right:
middle = (left+right)/2
if matrix[i][middle]<target:
left = middle+1
elif matrix[i][middle]>target:
right = middle-1
else:
return True
return False
else:
return True
return False
(253)240. Search a 2D Matrix II(Medium)
编写一个有效的算法,搜索m×n矩阵中的值。该矩阵具有以下属性:
每行中的整数按从左到右的升序排序。
每列中的整数按从上到下的顺序排序。
思路:
首先判断边界条件
从右上角开始,这样当target比当前元素小,就走左边,如果target比当前元素大,就走右边。
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if not matrix or not matrix[0]:
return False
row = 0
col = len(matrix[0])-1
while row<len(matrix) and col >= 0:
if matrix[row][col] <target:
row +=1
elif matrix[row][col]>target:
col -=1
elif matrix[row][col]==target:
return True
return False
(254)370. Range Addition(Medium)
ssume you have an array of length n initialized with all 0’s and are given k update operations.
Each operation is represented as a triplet: [startIndex, endIndex, inc] which increments each element of subarray A[startIndex … endIndex] (startIndex and endIndex inclusive) with inc.
Return the modified array after all k operations were executed.
Hint:
Thinking of using advanced data structures? You are thinking it too complicated.
For each update operation, do you really need to update all elements between i and j?
Update only the first and end element is sufficient.
The optimal time complexity is O(k + n) and uses O(1) extra space.
思路:
1、根据提示,每次只需要修改startIndex的值,和endldx+1的值就可以。因为通过利用prefix sum的累加性质,把+val的效果扩散到startindex以后,那么我们就需要在endidx+1及其以后的位置抵消掉这个影响。
def getModifiedArray(self,length,list):
result = [0]*(length+1)
for a in list:
result[a[0]] +=a[2]
result[a[1]+1] -=a[2]
for i in range(1,length):
result[i] +=result[i-1]
return result[::-1]
(255)79. Word Search(Medium)
Given a 2D board and a word, find if the word exists in the grid.
使用dfs,记得访问过的要标注
def exist(self, board, word):
"""
:type board: List[List[str]]
:type word: str
:rtype: bool
"""
if not board:
return False
for i in xrange(len(board)):
for j in xrange(len(board[0])):
if self.dfs(board, i, j, word):
return True
return False
# check whether can find word, start at (i,j) position
def dfs(self, board, i, j, word):
if len(word) == 0: # all the characters are checked
return True
if i<0 or i>=len(board) or j<0 or j>=len(board[0]) or word[0]!=board[i][j]:
return False
tmp = board[i][j] # first character is found, check the remaining part
board[i][j] = "#" # avoid visit agian
# check whether can find "word" along one direction
res = self.dfs(board, i+1, j, word[1:]) or self.dfs(board, i-1, j, word[1:]) \
or self.dfs(board, i, j+1, word[1:]) or self.dfs(board, i, j-1, word[1:])
board[i][j] = tmp
return res
(256)296. Best Meeting Point(Hard)
A group of two or more people wants to meet and minimize the total travel distance. You are given a 2D grid of values 0 or 1, where each 1 marks the home of someone in the group. The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.
Example:
Input:
1 - 0 - 0 - 0 - 1
| | | | |
0 - 0 - 0 - 0 - 0
| | | | |
0 - 0 - 1 - 0 - 0
Output: 6
Explanation: Given three people living at (0,0), (0,4), and (2,2):
The point (0,2) is an ideal meeting point, as the total travel distance
of 2+2+2=6 is minimal. So return 6.
Hint:
Try to solve it in one dimension first. How can this solution apply to the two dimension case?
思路:
这道题的我们先从一维开始想
两个点A和B,P在A,B区间之内距离都是AB,A,B区间之外距离都会大于AB
当我们在左右加上两个点C和D,这样当P在AB之间,四个点的距离之和都是AB+CD的距离,当P不在AB之间,距离一定会大于AB+CD的和。二维的情况就是两个一维的相加。
def minTotalDistance(self,grid):
rows,col = [],[]
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] ==1:
row.append(i)
col.append(j)
return self.TotalDistance(rows)+self.TotalDistance(cols)
def TotalDistances(self,v):
res = 0
v.sort()
i,j = 0,len(v)-1
while(i<j):
res+=v[j]-v[i]
j -=1
i+=1
return res
(257)361 Bomb Enemy(Midium)
给定2D网格,每个单元格可以是墙“W”,敌人“E”或空“0”(数字0),使用一个炸弹返回可以杀死的最大敌人。炸弹从种植点杀死同一行和列中的所有敌人,直到它撞到墙壁,因为墙壁太强而不能被摧毁。
请注意,您只能将炸弹放在空单元格中。
Example:
Input: [[“0”,“E”,“0”,“0”],[“E”,“0”,“W”,“E”],[“0”,“E”,“0”,“0”]]
Output: 3
Explanation: For the given grid,
0 E 0 0
E 0 W E
0 E 0 0
Placing a bomb at (1,1) kills 3 enemies.
思路:
最普通的做法就是,使用4个二维数组left、right、up、down分别表示上下左右分别能炸死多少人。然后使用两重循环确定max(left[i][j] + right[i][j] + up[i][j] + down[i][j])。时间复杂度为O(mn)空间复杂度为O(4m*n)
第二种做法是用二重循环遍历grid的时候,如果发现该格子处于第一行或者该格子的上面一个格子是墙,那么就把从该位置到下方第一个墙(或者边界)之间的敌人数目统计出来并且记录下来;同理,如果发现该格子处于第一列或者该格子的左边一个格子是墙,那么就把从该位置到右方第一个墙(或者边界)之间的敌人数目统计出来并且记录下来。之后如果发现该位置是空位置,说明可以放炸弹,就更新最终结果。该方法的巧妙之处在于每个纵区间和每个横区间内的敌人个数只会被统计一次。因此虽然在代码中两重循环内部还有一重循环,但是由于有if条件语句的存在,实际上总的时间复杂度仍然是O(m*n)。
def maxKilledEnemies(self,grid):
if not grid or not grid[0]:
return 0
row = len(grid)
col = len(grid[0])
ans = 0
for i in range(row):
for j in range(col):
colHits = 0
if i==0 or grid[i-1][j] =='W':
for k in range(i,row):
if grid[k][j] =='W':
berak
else:
colHits[j] +=(grid[k][j] == 'E')
rowHits = 0
if j==0 or grid[i][j-1]=='W':
for k in range(j,col):
if grid[i][k] =='W':
break
else:
rowHits +=(grid[i][k] =='E')
if grid[i][j]=='0':
ans = max(ans,rowHit+colHit)
return ans
(258)317. Shortest Distance from All Buildings(Hard)(未写)
You want to build a house on an empty land which reaches all buildings in the shortest amount of distance. You can only move up, down, left and right. You are given a 2D grid of values 0, 1 or 2, where:
Each 0 marks an empty land which you can pass by freely.
Each 1 marks a building which you cannot pass through.
Each 2 marks an obstacle which you cannot pass through.
Example:
(259)302 Smallest Rectangle Enclosing Black Pixels(Hard)(未写)
(260)36.有效的数独(Medium)
横竖不能包含相同数字,每个小的九宫格里面不能包含相同数字
给定一个九宫格,判断是不是合法的数独
思路:
1、使用一个set来存储已经存在的元素
2、使用(i/3,j/3)来表示小的九宫格
big = set()
for i in xrange(0,9):
for j in xrange(0,9):
if board[i][j]!='.':
#cur is string
cur = board[i][j]
if (i,cur) in big or (cur,j) in big or (i/3,j/3,cur) in big:
return False
big.add((i,cur))
big.add((cur,j))
big.add((i/3,j/3,cur))
return True
(261)37.数独解算器(Hard)
思路:
1、需要有个判别器,判别加入元素后会不会是合法的数独,判断小九宫格有点困难
2、接着使用递归,加入元素
def solveSudoku(self, board):
"""
:type board: List[List[str]]
:rtype: None Do not return anything, modify board in-place instead.
"""
def isVaild(i,j,c):
for k in range(9):
if (board[i][k]==c): return False
if (board[k][j]==c): return False
if (board[3 * (i / 3) + k / 3][3 * (j / 3) + k % 3]==c): return False
return True
def slove():
for i in range(9):
for j in range(9):
if board[i][j] =='.':
for c in range(1,10):
if (isVaild(i,j,str(c))):
board[i][j] = str(c)
else:
continue
if (slove()==False):
board[i][j] = '.'
else:
return True
return False
return True
slove()
未完,待续。。。
此篇由于篇幅限制,转入第二篇,(包括有常见的面试题哦,第二篇)