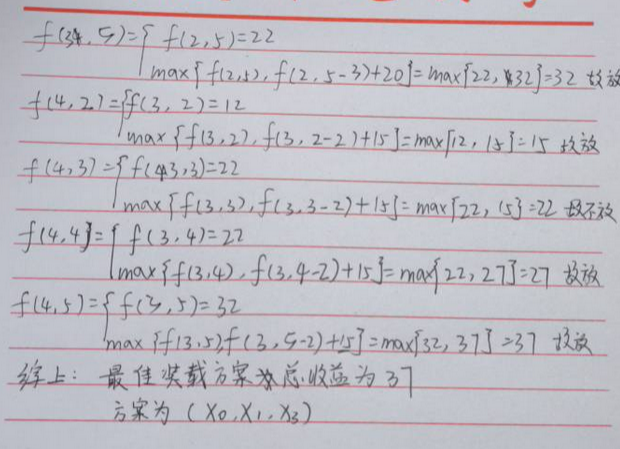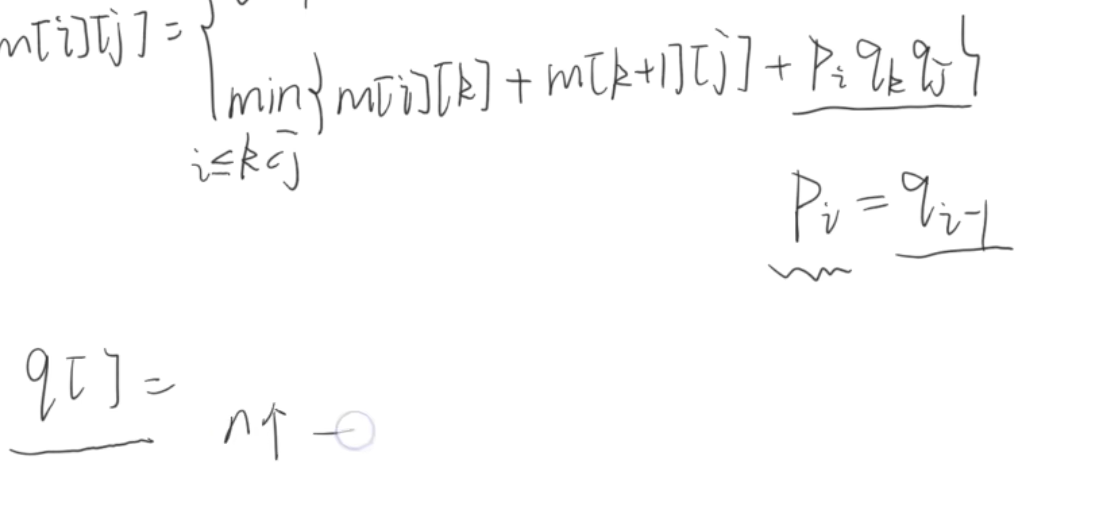程序设计竞赛

0x00 基本操作指南

输入的结束,推荐使用下面的非~：位运算符，按位取反；只有当x值为-1时（-1的补码：11111111），~x的值才为0

while(~scanf("%d%d", &a, &b))

指定数据个数结束，提高程序编写效率

int main(){
    int n, a, b;
    scanf("%d", &n);
    while(n -- ){
        
    }
}

以特定元素作结束符，以读取到0结束为例

while(~scanf("%d", &n) && n)   

• 测试的两种方法：

  • 在程序中加入测试代码

  #include<stdio.h>
  #define mytest
  int main(){
      int n;
      #ifdef mytest
  	freopen("test.in", "r", stdin);   //将stdin重定向到test.in文件，file redirect 不需要从键盘输入了
  	//freopen("test.out", "w", stdout);
  #endif
      while(~scanf("%d", &n) && n){
          printf("%d\n", n * n);
      }
      return 0;
  }
  

  • 在命令行中重定向 好处在于不需要修改源代码适合测多个文件

  #include<stdio.h>
  int main(){
      int n;
      while(~scanf("%d", &n) && n){
          printf("%d\n", n * n);
      }
      return 0;
  }
  

  上面文件abc.cpp 一定注意要把源文件进行编译 生成exe文件

  然后在相同位置 创建test.in文件 记事本

  在该位置进入到当前目录 执行命令

  abc < test1.in > test1.out

  

  < : 输入

  > : 输出重定向

  把结果存入到test1.out

  

  然后对比我们的结果和答案(答案是我们预测的结果）是否相同

  fc test1.out answer.out

  

  命令进阶版

  创建xxx.bat文件 批量化执行命令脚本

  abc <test1.in> test1.out
  abc <test2.in> test2.out
  abc <test3.in> test3.out
  fc test1.out answer1.out
  fc test2.out answer2.out
  fc test3.out answer3.out
  pause
  

提速：

1. 使用STL库
2. 不使用动态调试 而是通过打印中间信息
3. 模板

算法证明 ：

• 归纳法
• 反证法

在c++ 中引入c的函数进行提速文件头

#include<iostream>
#include<cstdio>
#include<cmath>

using namespace std;

int main(){
    
    return 0;
}

• 题目类型：
  • Ad Hoc，杂题；
  • Complete Search（Iterative/Recursive)，穷举搜索
  • Divide and Conquer，分治法
  • Greedy，贪心法
  • Dynamic Programming，动态规划
  • Graph，图论
  • Mathmatics，数学
  • String Processing，字符串处理
  • Computation Geometry，计算几何
  • Some Harder，罕见问题
• 代码规范
  • 少用

课本推荐的题目全部要做掉 没时间做来上课干嘛

int最大：2147483647 20多个亿

• 报错：

RE：Runtime Error 运行错误 大部分都是数组越界 特殊：除0越界

MLE：数组开太大

• 区分scanf和cin的区别

主要是在输入一个数字+一段字符时容易出错

cin cout 提速代码： 数据达到百万级 注意：如果进行了加速 scanf 和printf就必须禁用

ios::sync_with_stdio(flase);
cin.tie(0);
cout.tie(0);

• bug 避坑

如果创建副本 会导致执行相同的exe文件 所以需要修改前面的命名

• 大数据测试方法：

记事本打不开 直接死掉

使用fopen

freopen("1.in","r",stdin);
//输出
freopen("1.txt", "w", stdout);

• 数组建议从1开始 因为在搜索的时候 地图如果从0开始可能有问题

• double 类型的数据 在读入的时候是lf 但是输出本身就是f

0x01 算法分析

• 多项式复杂度
• 指数复杂度(一般是暴力求解出现)

$$O(2^n)<O(n!)<O(n^n)$$

最快的方法：打表法

只输出结果

打表法：以素数个数求解

float Sum(float list[], const int n){
    float tempsum = 0.0;
    count ++;
    for(int i = 0; i < n; i++){
        count ++;
        tempsum += list[i];
        count ++;
    }
    count ++;
    count ++;
    return tempsum;
}

确定问题的规模 根据count ++的数量 T(n) = 2 * n + 3

$$\begin{gathered} f(n)=2n+3=O(n) \\ 当n\ge 3时 \end{gathered}$$

一点一点放
$$\begin{gathered} 10n^2+4n+2 \\ 当n\ge 2时，原式\le 10n^2+5n \\ 当n\ge 5是，上式\le 10n^2+n^2=11n^2=>O(n^2) \end{gathered}$$

反证法
$$10n^2+9\ne O(n)$$

• 矩阵乘法

for(i = 0; i < n; i++){
    for(j = 0; j < n; j++){
        c[i][j] = 0;
        for(k = 2; k < n; k++){
            xxx
            ...
            xxx
        }
    }
}

O（n次方）

主方法：

理解与应用

证明不会重点考查

除法相对于其他运算会非常慢 所以一般采用移位进行做除法

增长率计算方法：https://blog.csdn.net/qq_37657182/article/details/102826437

0x02 STL和基本数据结构

• STL

Standard Template Library，C++的标准模板库，竞赛中常用的数据结构和算法可以直接调用。

容器：存放数据的，如Vector list queue stack map(映射) set（集合）

​ 容器适配器：在别的容器的基础上加上外壳 把原有的容器的基础上做一些限制和处理 如stack queue priority_queue

​ 关联容器：set map multiset（关键词可以重复） multimap

​ 无序关联容器：真正使用哈希表 从c++11开始 在关联容器的前面+unordered_

​ 通用功能：

​ begin() 存在数据 end() 无数据

迭代器：容器和算法之间的桥梁，可以认为是一个特殊的指针，指明数据的来源和去处

算法：如sort

函数对象：谓词，比如在排序的时候按照从大到小还是从小到大 利用函数对象进行说明

在竞赛中尽量不用vector 推荐数组 Vector为动态数组

栈

hdu 1237 自己做

队列

大量删除操作 绝对别用vector

集合

set和map 本质是红黑树 Red Black Tree

本身是有序的

1 3 5 7 9

使用必须有序

A.lower_bound(k) x>=

A.upper_bound() x >

hdu 2094

凡是选手进第一个集合

失败者进第二个集合

最终比较两个集合的差 如果差是1 产生冠军 否则没有冠军

map

关联容器 键值对 key => value 映射

hdu 2648

homework

提交解题报告 用到哪些原理 基础知识 算法 源程序

每一个程序至少5个测试数据 需要大规模测试数据 不能常规的

0x03 排序

插入排序

打扑克牌的插入方法，在部分有序的数列中不断插入新的元素

//c++
template<class Type>   //把类型抽象成参数  不再依赖于具体的数据类型
void insertion_sort(Type *a, int n){
    Type key;
    for(int i = 1; i < n; i++){
        key = a[i];
        int j = i - 1;
        while(j >= 0 && a[j] > key){
            a[j + 1] = a[j];
            j--;
        }
        a[i + 1] = key;
    }
}

归并排序（Merge Sort)

快速排序

0x04 搜索技术

BFS DFS 深搜 广搜

本质就是暴力搜索，走投无路就暴搜

广搜索：一层一层拨开，先离我距离为1的 再距离我为我2的 采用队列！

BFS

宽搜：绝对不要自己手写队列

/*
  来存一个BFS的模板 
*/ 
int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};
int vis[1005][1005];   //做标记 是否访问过 
struct P{
    int x,y,z;
};

bool BFS(int x, int y, int mid){
	queue<P> q;
	q.push({x, y, a[x][y]});
	while(!q.empty()){
		P x = q.front();
		q.pop();
		//
		if(a[x.x][x.y] <= mid){
			//如果走到头了   直接返回true 
			if(x.x == n) return true;
			//没走到头 继续往下走
			for(int k = 0; k < 4; k++){
				int nx = x.x + dx[k];
				int ny = x.y + dy[k];
				//矩阵范围判断 
				if(nx >= 1 && ny >= 1 && nx <= n && ny <= m && vis[nx][ny] == 0 && a[nx][ny] <= mid){
					q.push({nx, ny, max(x.z, a[nx][ny])});
					vis[nx][ny] = 1; //表示访问过了 
				}
			} 
			 
		} 
	}
    return false; 
}

DFS

深搜：自己手写栈

回溯与剪枝

如果明确知道某个分支下面不可行 则不再向下走

八皇后问题：

不在一个斜线：
$$|i-j|=|x_i-x_j|$$
剪枝的过程中要不断check

bool check(int c, int r){
for(int i = 0; i < r; i++){
  if(col[i] != c && abs(i - r) != abs(col[i] - c)){

  }
}
}

深度迭代

ID A*

A star

曼哈顿启发式算法
$$|x_1-x_2|+|y_1-y_2|$$

双向广搜

0x05 递推方程

分解问题的规模，以及问题的相关性

列出递推方程进行求解问题

• 必须有一个初始条件

• 计算时的常用三种方法：

  • 替换法：首先猜测递推式的解，然后使用归纳法证明，如解决汉诺塔问题
    $$T(n)=\{\begin{array}{l}1n=1\\ 2T(n-1)+1n>1\end{array}$$

    void Hanoi(int n, tower x, tower y, tower z){
        if(n){
            Hanoi(n-1, x, y, z);
            Move(n, x, y);
            Hanoi(n-1, z, y, x);
        }
    }
    

  • 迭代法：针对T（n）进行推导 不带入具体数据

  • 主方法：

递归树：把中间的节点一分为2

0x06 高级数据结构

并查集

指的是不想交的集合 disjoint

经典应用：连通子图、最小生成树Kruskal算法 最近共同祖先

实现代码：

int parent[105];

// 并查集初始化
void UFset() {
    for (int i = 1; i <= n; i++) {
        parent[i] = -1;
    }
}

int find(int i) {
	//update the value of temp
    int temp;
    for (temp = i; parent[temp] >= 0; temp = parent[temp]);
    
    while (temp != i) {
        int t = parent[i];
        parent[i] = temp;
        i = t;
    }
    return temp;
}

// 合并两个集合
void merge(int a, int b) {
    int r1 = find(a);
    int r2 = find(b);
    int tmp = parent[r1] + parent[r2];
    if (parent[r1] > parent[r2]) {
        parent[r1] = r2;
        parent[r2] = tmp;
    } else {
        parent[r2] = r1;
        parent[r1] = tmp;
    }
}

// Kruskal算法求最小生成树的总权值
int kruskal() {
    int sumWeight = 0;

    UFset(); // 初始化并查集
    for (int i = 1; i <= m; i++) {
        int u = edges[i].u;
        int v = edges[i].v;
        // 如果 u 和 v 不在同一个集合中，选择该边
        if (find(u) != find(v)) {
            sumWeight += edges[i].w;
            merge(u, v); // 合并 u 和 v 所在的集合
            cnt++;
        }
        // 已选择的边数达到 n-1 条时，退出循环
        if (cnt == n - 1) {
            break;
        }
    }
    return sumWeight;
}

二叉树

后序遍历：

先往下走 先左后右 无右向上

二叉搜索树

BST，比左孩子大，比右孩子小

红黑树是其中一种 set和map就是基于红黑树的一种

Treap树：在二叉搜索树的基础上增加了优先级

意味着成为一个树堆（大根堆、小根堆）

旋转：

void rotate(Node* &o, int d){
    Node *k = o -> son[d ^ 1];
    o 
}

注意son[0] 表示左孩子

son[1] 表示右孩子

在竞赛中尽量别用平衡二叉树 太繁琐

退化树

Treap树（堆）

插入：

删除：

struct 可以视为一个类

#include <iostream>

using namespace std;

struct Node{
    int x, y;
    Node(int x, int y){
        this -> x = x;
        this -> y = y;
    }
    void print(){
        cout << x << y;
    }
}

//或者真正用类  但是注意其他的方法都是private 所以需要先声明权限
class Node{
    public:
    int x, y;
    Node(int x, int y){
        this -> x = x;
        this -> y = y;
    }
    //或者：Node(int x, int y):x(x),y(y){}
    void print(){
        cout << x << y;
    }
}
int main(){
    
}

伸展树Splay

不要求树是平衡的 允许把任何结点放到根上去

单旋

三点共线旋

三点不共线旋

线段树

考查较少

树状数组

往往和折半查找混合在一起用

0x07 分治法*

一般方法

分-将要求解的较大规模的问题分割成k个更小规模的子问题 注意子问题和子问题之间是独立的

合-将求解出的小规模的问题的解合并为一个更大规模问题的解，自底向上逐步求出原来问题的解

SolutionType DandC(ProblemType P){
    ProblemType P1, P2,..., Pk;
    if(Small(P)) return S(P);
    else{
        Divide(P, P1, P2, P3, ... , Pk);
        Return Combine(DandC(P1), DandC(P2), ... , DandC(Pk));
    }
}

求最大最小元

说白了就是求最大值和最小值

传统法：规模不大可以用

maxmin(float a[], int n){
    max = min = a[0];
    for(int i = 1; i < n; i++){
        if(max < a[i]) max = a[i];
        else if(min > a[i]) min = a[i];
    }
}

分治法：

构造树，每个子树的范围为除以二

扩展：求次最大元 次最小元

#include <iostream>
#include <climits>

using namespace std;

const int N = 100;
float a[N];

void maxmin(int left, int right, float &max, float &second_max, float &min, float &second_min) {
    if (left == right) {
        max = a[left];
        second_max = INT_MIN;
        min = a[left];
        second_min = INT_MAX;
    } else if (left + 1 == right) {
        if (a[left] > a[right]) {
            max = a[left];
            second_max = a[right];
            min = a[right];
            second_min = a[left];
        } else {
            max = a[right];
            second_max = a[left];
            min = a[left];
            second_min = a[right];
        }
    } else {
        int mid = left + (right - left) / 2;
        float lmax, left_second_max, lmin, left_second_min;
        float rmax, right_second_max, rmin, right_second_min;
        maxmin(left, mid, lmax, left_second_max, lmin, left_second_min);
        maxmin(mid + 1, right, rmax, right_second_max, rmin, right_second_min);

        // Update max
        if (lmax > rmax) {
            max = lmax;
            // Check if rmax is greater than left_second_max or not
            if (rmax > left_second_max) {
                second_max = rmax;
            } else {
                second_max = left_second_max;
            }
        } else {
            max = rmax;
            // Check if lmax is greater than right_second_max or not
            if (lmax > right_second_max) {
                second_max = lmax;
            } else {
                second_max = right_second_max;
            }
        }

        // Update min
        if (lmin < rmin) {
            min = lmin;
            // Check if rmin is less than left_second_min or not
            if (rmin < left_second_min) {
                second_min = rmin;
            } else {
                second_min = left_second_min;
            }
        } else {
            min = rmin;
            // Check if lmin is less than right_second_min or not
            if (lmin < right_second_min) {
                second_min = lmin;
            } else {
                second_min = right_second_min;
            }
        }
    }
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    float max, second_max, min, second_min;
    maxmin(0, n - 1, max, second_max, min, second_min);

    cout << max << " " << second_max << endl;
    cout << second_min << " " << min << endl;

    return 0;
}

二分搜索

每次砍一半，效率较高

扩展：三分搜索

#include <iostream>

using namespace std;

/*
三分搜索
*/

const int N = 101;
int a[N];
int n;

int ternarySearch(int find){
	int left = 0;
	int right = n - 1;
	
	while(left <= right){
		int mid1 = left + (right - left) / 3;
		int mid2 = right - (right - left) / 3;
		
		//给出结果 
		if(a[mid1] == find){
			return mid1;
		}
		if(a[mid2] == find){
			return mid2;
		}
		
		//调整查找范围
		if(find < a[mid1]){
			right = mid1 - 1;
		} 
		else if(find > a[mid2]){
			left = mid2 + 1;
		}
		//在中间 
		else{
			left = mid1 + 1;
			right = mid2 - 1;
		}
		
	}
	return -1; 
}


int main(){
	cin >> n;   
	for(int i = 0; i < n; i++){
		cin >> a[i];
	}
	int find;
	cin >> find;
	int re = ternarySearch(find);
	cout << re;
	return 0;
}

排序问题

• 二路归并排序

两段有序序列

然后谁小把谁拉下来

//Merge

• 快速排序

划分：选定一个记录作为轴值，以轴值为基准将整个序列划分为两个子序列，把比轴值小的放左边，比轴值大的放右边

左右寻找的方法：最左边放i 最右边放j 然后同时向中间缩，根据大小不断交换

void QuickSort(int a[], int p, int r){
    if(p < r){
        int q = Partition(a, p, r);
        QuickSort(a, p, p - 1);  //对左半段排序
        QuickSort(a, p + 1, r);  //对右半段排序
    }
}

int Partition(int a[], int p, int r){
    int i = p, j = r + 1;
    int x = a[p];
    while(ture){
        while(a[++i] < x);
        while(a[--j] > x);
        
    }
}

主元选择：

• 随机选(不做要求)

• 线性时间选择

int RandomizedSelect(int a[], int p, int r, int k){
    if(p == r) return a[p];
    int i = RandomizedPartition(a, p, r);
    j = i - p + 1;
    if(k <= j) return RandomizedSelect(a, p, i, k);
    else return RandomizedSelect(a, i + 1, r, k - j);
}

划分：n -> 3/4 n

五个一组进行划分 然后每组组内进行排序

1 2 3 4 5

2 3 4 5 6

. . . | . . .

---

. . . | . . .

. . . | . . .

这样划分后左上角一定比中间的小 右下角一定比中间的大

前面找一个大的 与后面找一个小的地方进行交换

原理：

选择一个基准元素

然后从两端向基准元素探测，直到右边的比基准元素小，左边的比基准元素大，我们进行比较，如果这两个探测的元素还是原位置，没有交界，则这两个元素互换位置。因为我们的目的就是基准元素左边的比它小，右边的比它大

当ij相遇，则交换基准元素位置和相遇位置元素

对左右分割段采用递归调用重复操作

完整代码：

#include <iostream> 
using namespace std;

/**
* 分治法实现快速排序
**/ 
int a[100005];
int n;
 
int Partition(int l, int r){
	int i = l - 1;
	int j = r + 1;
	int x = i + j >> 1; //选择主元      右除 
	while(i < j){
		do{
			i ++;
		}while(a[i] < a[x]);
		do{
			j --;
		}while(a[j] > a[x]);
		if(i < j) swap(a[i], a[j]);
	}
	return j; 
} 
 
void quickSort(int l, int r){
	if(l < r){
		//pos作为分隔元素 对前后进行排练 
		int pos = Partition(l, r);
		quickSort(l, pos);
		quickSort(pos + 1, r); 
	}
}
//数组就从下标为0开始吧 
int main(){
	cin >> n;
	for(int i = 0; i < n; i ++){
		cin >> a[i];
	}	
	quickSort(0, n - 1);
	
	for(int i = 0; i < n; i++){
		cout << a[i] << " ";
	}
	return 0;
}

选择问题

选第k小

分治法思想：

一趟划分 分成两个左右子表 主元是随机选的

然后主元+左子表个数为p 如果k=p直接找到 如果k<p 则只在前面找 后面直接舍弃

注意如果k > p时 在右边找的话要找第p-k小

二次选中法确定主元

斯特拉森

0x08 动态规划（Dynamic Programming，DP）*

定义

运筹学的一个分支

与分治法的区别：

• 子问题与子问题之间有交叉，重叠子问题 只解一次 => 所以效率比较高

• 并且这个问题满足最优性原理（问题的最优解包含了子问题的最优解）

• 无后向性

满足上面三个条件，可用DP

实质就是动态的表格题， 用数组来保存结果, 就是在填dp数组的表

表格是动态的，每次都在修订

大部分是从后往前搞，把原问题转化为子问题，缩小问题规模 即自底向上

硬币组合

0/1 背包问题

特殊点在于物品无法分割 ，只能全放或者全不放，这如果使用贪心算法就可能会存在一些空间的过度浪费

从右边往左边选f（j，X） = max{f(j-1, X), f(j-1, X-wj) + pj}

两步：

dp[i][j] = max{dp[i][j-1], dp[i-wj][j-1] + vj}

构造两个二维表格进行存储数据

解释含义：

c 表示当背包容量为c的时候 能放入的最大价值

i 表示只选择i个的物品的情况，注意这里按顺序选择就好 比如i = 2就是计算装前两个的情况

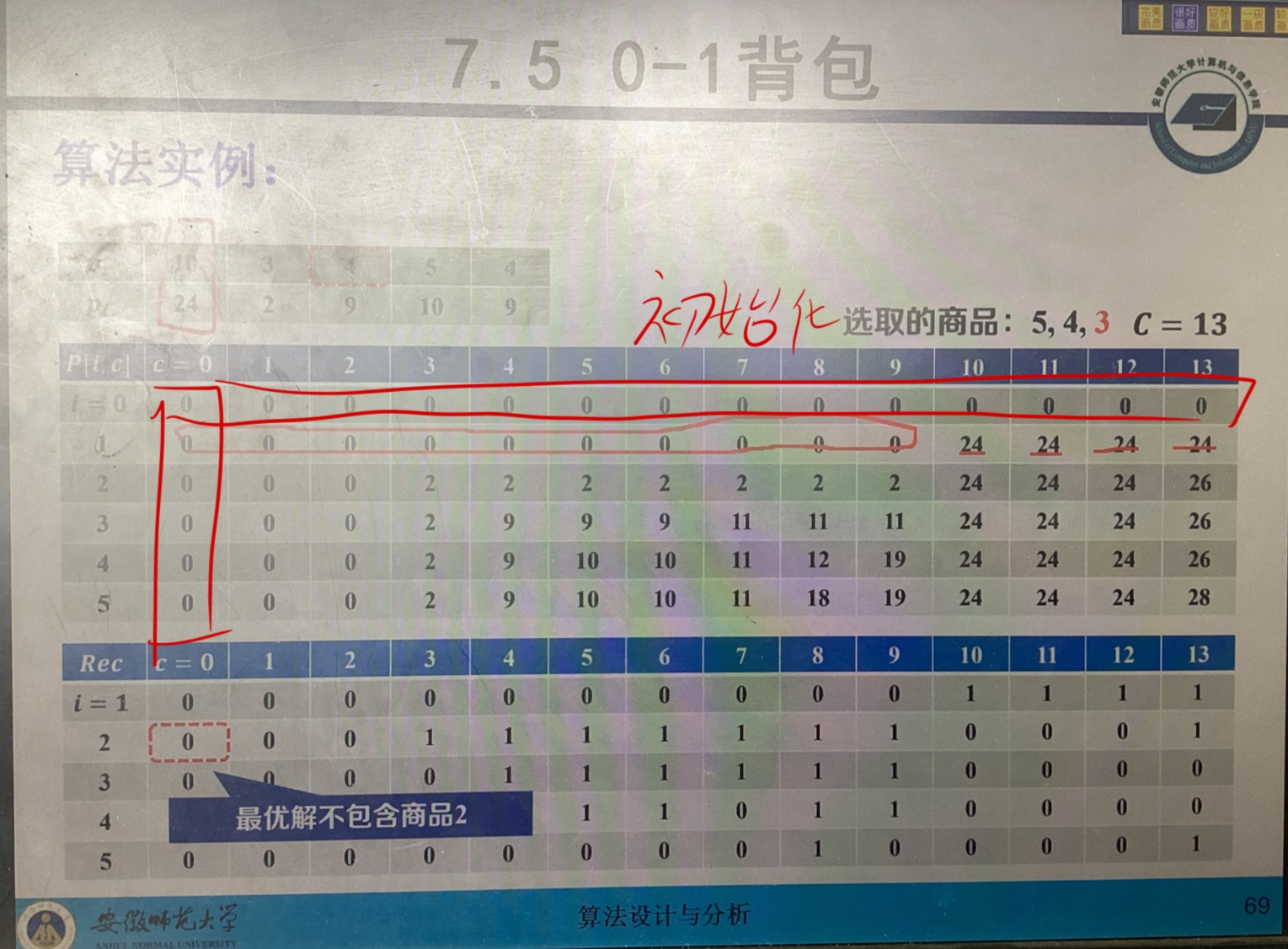
表格数据推导：

当i = 1的时候，只判断第1个物品，c为1到9都装不下 当c=10 也就是背包容量为10的时候，可以装装下，价值为24，当背包容量继续扩大，那包装下的啊

当i = 2的时候，判断第1个和第2个物品，当c=1的时候，针对物品2列式子，有两种可能 针对上一个判断

f（2,1）= f(1, 1-3) + 2 = f(1, -2) + 2 装入

f（2,1） = f（1，1） 不装入

在f函数中第一个参数表示第几个物品，第二个参数表示背包容量情况

因为-2不符合实际要求，所以只能不装入，值为f（1,1）= 0

以此类推，当c=3时

f（2,3）=f(1, 3-3) + 2 = f(1, 0) + 2 = 2 装入

f（2,3）=f（1,3） = 0 不装入

选较大值 即为2

代码实现：

//初始化  n行 m列
for(int i = 0; i <= n; i++) f[i][0] = 0;
for(int i = 0; i <= m; i++) f[0][i] = 0;
for(int i = 1; i <= n; i++){
    for(int j = 1; j <= m; j++){
        //放
        if(j >= w[i]){
            f[i][j] = max(f[i - 1][j - w[i]] + p[i], f[i - 1][j]);
        }
        //不放
        else{
            f[i][j] = f[i - 1][j];
        }
    }
}
printf("%d\n", f[n][m]);

例题：

参考：https://cloud.tencent.com/developer/article/2109840

滚动数组

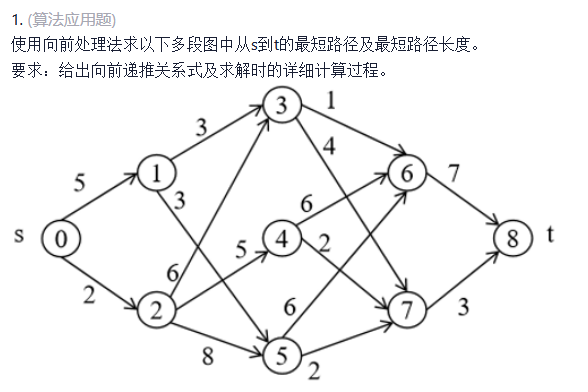
最短路径问题

例题：

从结果往前推，一层一层进行

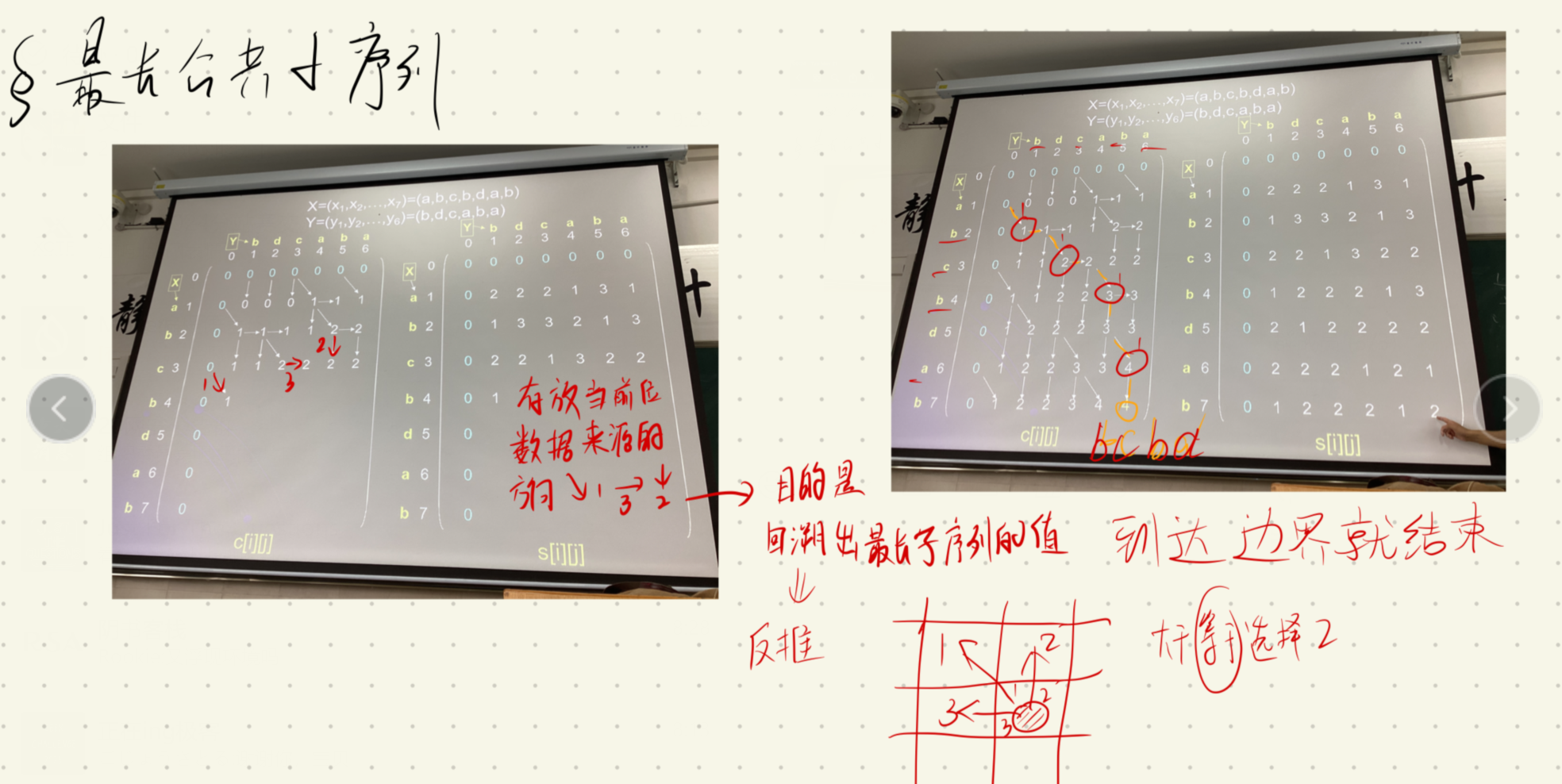
最长公共子序列（LCS）

实例：

X : A B C B D A B

y : B D C A B A

子序列的定义就是按照下标严格递增

考察末尾字符

如果想要进行切分，条件在于末尾字符要相同，否则去掉末尾字符可能会遗漏一些公共子序列

相等的话则一定是公共子序列啦，所以 是删除后求最优解 然后结果加上末尾相同的个数

构建过程：

回溯代码：

void LCS(int i, int j, X, S){
    if(i == 0 || j == 0) return;
    if(S[i][j] == 1){
        LCS(i - 1, j - 1);
        cout << a[i];
    }
    else if(S[i][j] == 2) LCS(i - 1, j);
    else LSC(i, j - 1);
}

时间复杂度 ： O（m + n)

例题：

简单来说就是如果行列的字符相同 则是左上角的值+1

如果不相同，则是左边和上面的值比较 取较大值 如果两值相等 直接数据来源于上方

参考：https://blog.csdn.net/2301_79582459/article/details/139198609

最少拦截问题 => LIS 最长递增子序列

hdu1257

举例:

3 1 5 2 4 6

递增序列：
1 2 4 6 （LIS）
1 5 6
3 4 6
1 5

以3结尾：dp[0] = 1 数据长度

以1结尾：dp[1] = 1

dp[2] = 2

dp[i] = max{dp[i], dp[j]} + 1 (a[j] < a[i])

1. 找出最优解的性质，并刻画其结构特征
2. 递归地定义最优值
3. 以自底向上

存模板：

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N],q[N];     //a是原数组  q是需要维护的数组存储递增子序列 
int n;
int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    int len = 0;
    for (int i = 0; i < n; i ++ )
    {
        int l = 0, r = len;
        //二分 不理解？？ 
        while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i]) l = mid;
            else r = mid - 1;
    	}
        len = max(len, r + 1);
        q[r + 1] = a[i];    //不断给q插值 
    }
    printf("%d\n", len);
    return 0;
}

矩阵连乘问题

每行 和 每列 连乘相加 放到元素位置

乘法次数 10 * 100 100 * 5 = > 10 * 100 * 5 ！是这样的

在位置k处切一道 左边最小 + 右边最小

画表 记录 在数组中

两个矩阵为4,6 6,10

次数为4 * 6 * 10

一般设置两个表

一个存放最优解的值 另一个存放如何切分才能得到最优解

设置数组

对于一系列矩阵
$$\begin{gathered} A_i{A}_{i+1}...A_j \\ m[i][j]表示A_i到A_j的最小乘法次数 \end{gathered}$$

对于n个矩阵 使用q这个一维数组 n+1个元素就够了

例题：

0x09 基础语法

引用：

int a = 5;
int &x = a;   //x作为a的一个引用
x = 4;
printf("%d", a);  //输出是4

0x10 二分答案

概念

使用二分查找需要满足：一定要有序 单调性

识别题目：存在最大的最少 最少的最大这类字眼

#include <cstdio>
int a[1000000], n;  //全局变量自动赋值为0
//如果是局部变量 记得赋值0 然后使用sum++ 这类函数 否则是随机数进行++

/**
 * 基本二分查找实现
*/
int check(int key){
    int left = 0, right = n - 1, mid;
    while(left <= right){   //一定是小于等于
        mid = (left + right) >> 1;   //这就是除2  其实右移和除2不是一回事 因为在正数情况下无影响 负数存在向0取整-3 右移是-2  除2是-1
        if(key == a[mid]) return 1;
        if(key > a[mid]){
            left = mid + 1;
        }
        else if(key < a[mid]){
            right = mid - 1;
        }

    }
    return 0;   //在win下不写也能过 但是在Linux中有问题
}

例题：洛谷 P1873

看完题目一定要看一下题目范围 初步判断一下这个题目是否需要开long long

#include <bits/stdc++.h>
using namespace std;

/**
 * 定义变量：
 * 1. 尽量全局
 * 2. 尽量见词知意
 * 
*/
int n, m, l, r = 1e9, mid;    //1e9=10的9次方
long long a[1000005], sum;

int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++){
        scanf("%lld", &a[i]);
    }
    while(l <= r){ //二分结果：1. rl位置关系 2. l = r + 1 
        sum = 0;  //清零
        mid = (l + r) / 2;
        for(int i = 1; i <= n; i ++){
            if(a[i] > mid){
                sum += a[i] - mid;
            }
        }
        //可以写sum >= m  然后可以删除掉最后else的部分 因为相等时l定住不动 r一点点靠近
        if(sum > m){
            l = mid + 1;
        }
        else if(sum < m){
            r = mid - 1;
        }
        //仅仅这个题中符合该条件
        else{
            cout << mid;
            return 0;
        }
    }
    cout << r;   //需要分析清楚
    return 0;
}

P1182 数列分段 SectionII

P1824 进击的奶牛

//P1824 进击的奶牛
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,c,a[100005];
int check(int mid){
	int pos=1;
	int k=c;
	while(--k){
		pos=lower_bound(a+1, a+n+1, a[pos]+mid)-a;
		if(pos==n+1) {
			return 0;
		}
	}
	return 1;	
}
int main(){
	scanf("%d%d",&n,&c);
	for(int i=1; i<=n; i++) scanf("%d",&a[i]);
	sort(a+1, a+n+1);
	int l=1,r=1e9;
	while(l<=r){
		int mid=(l+r)>>1;
		if(check(mid)) l=mid+1;
		else r=mid-1;		
	}
	cout<<r;
	return 0;
}

/*
二分答案
这里二分的是奶牛之间的间隔 

*/

练习

课后oj例题：

A：奶茶店选址

B：野外探险

分析：

D天活动，N份干粮，N份粮食进行编号，小明从小到大开始吃 花费D天全部吃完

每份粮食能量值为Hi 每天获得能量是当天吃下的所有干粮的能量值之和 （每天吃或者不吃 吃多少都不一定）

每天的能量会在第二天开始时消耗掉一半 注意是整除的一半

设计方案，让小明获得能量值最小的那一天最大 ！ 关键字眼（最小的最大）

思考：

对答案进行二分

答案的最小值是1 最大一定要设置的大一点 预测一下答案范围

解决：

每一天都要大于mid 所以不断吃 直到大于mid换下一天 看看能否正好满足天数

代码：

#include<bits/stdc++.h>

using namespace std;
int N, D;
int a[50005];

int check(int mid){
	int k = 1;  //表示第几份食物 
	int sum[D + 5];
	//该函数的作用是给sum赋值为0  N个食物  D天 
	memset(sum, 0, sizeof(sum));
	//第1天灌食   因为mid是最小 所以每天获得的大于mid才能到下一天 
	while(sum[1] < mid && k <= N){
		sum[1] += a[k];   //吃能量 
		k++;
	} 
	if(sum[1] < mid){
		return 0;
	}    
	//第2天往后 
	for(int i = 2; i <= D; i++){
		sum[i] = sum[i - 1] / 2;      //获取前一天的能量值 
		while(sum[i] < mid && k <= N){    //注意啊 N份食物 可以一直吃 所以有等号 要不然结果不对！ 
			sum[i] += a[k];
			k++; 
		} 
		if(sum[i] < mid){
			return 0;
		}      
	} 
	return 1;
}

int main(){
	scanf("%d%d", &N, &D); 
	for(int i = 1; i <= N ; i++){
		scanf("%d", &a[i]); 
	}
	//需要思考 二分的是答案 对答案进行二分查找 作为最后的结果不断带进场景中做check 
	int l = 1, r = 1e9; 
	while(l <= r){
		int mid = (l + r) >> 1;
		if(check(mid)){
			l = mid + 1;
		} 
		else r = mid - 1;
	} 
	cout << r;
	return 0;
} 

C：龙年邮票

分析：集邮票活动，一套完整的龙年邮票共有n种不同的造型

小明有第i种造型的邮票ai张，m张万能邮票

万能邮票可以抵任意一张，问一共能集齐多少套邮票

非常像之前支付宝的集五福啊！还有一个万能福

思考：

同样是对答案进行二分查找

代码：(有点想不到)

#include <bits/stdc++.h>

using namespace std;

int n, m;
int a[100]; 
int b[100];


int check(int mid){
	int sum=0;     //记录万能票使用数量 
    memcpy(b,a,sizeof b); //把a的值赋给b  对b进行操作 
    for(int i = 1;i <= n; i++)
    {
        int x = mid - a[i];   //套数 - 当前品种数量    1 2 3   3       0 1
		//如果套数小于当前品种邮票数量 正常执行 检测下一个品种的邮票 
        if(x <= 0)
          continue;
        //如果当前品种邮票不足以支撑目标套数 则启动万能票  差x张     2        3
        else
        {
            for(int j = 1; j <= n; j++)
            {
                if(i != j && b[j] < x) //如果存在其他品种 比当前差值还少 直接完蛋 因为万能票只能用一次 
                  return 0;
                else if(i != j)     //否则 对其他品种减去万能票数 
                   b[j] -= x;
            }
        }
        sum += x;
    }
    if(sum <= m)
      return 1;
    return 0;
	
	
}

int main(){
	cin >> n >> m;
	for(int i = 1; i <= n; i++){
		cin >> a[i];
	}
	//把所有存在的邮票 按数量从小到大排列 
	sort(a + 1, a + 1 + n);
	
	int l = 1, r = 1e9;
	while(l <= r){
		int mid = (l + r) >> 1;
		if(check(mid)){
			l = mid + 1;
		}
		else{
			r = mid - 1;
		}
	}
	cout << r;
	return 0;
} 

D : 消耗的能量

分析：n行 m列数字矩阵 第一行均为0 从第一行出发 到第n行任意位置结束

规定消耗能量为每行行走过的格子各自和的最大值

求所有路径中，小明消耗能量的最小是多少

思考：最大 最小！！！ 二分答案的关键词！！！

然后涉及到路径 那么我们考虑使用bfs 去探测路径

然后在探测路径的过程中，需要去对每一行的横向进行能量探测，如果能量大于我们的二分答案值 则换下一个答案

#include <bits/stdc++.h>

using namespace std;

int n, m;
int a[1005][1005];


/*
  来存一个BFS的模板 
*/ 
int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};
int vis[1005][1005];   //做标记 是否访问过 
struct P{
    int x,y,z;
};

bool BFS(int x, int y, int mid){
	queue<P> q;
	q.push({x, y, a[x][y]});
	while(!q.empty()){
		P x = q.front();
		q.pop();
		//
		if(a[x.x][x.y] <= mid){
			//如果走到头了   直接返回true 
			if(x.x == n) return true;
			//没走到头 继续往下走
			for(int k = 0; k < 4; k++){
				int nx = x.x + dx[k];
				int ny = x.y + dy[k];
				//矩阵范围判断 
				if(nx >= 1 && ny >= 1 && nx <= n && ny <= m && vis[nx][ny] == 0 && a[nx][ny] <= mid){
					q.push({nx, ny, max(x.z, a[nx][ny])});
					vis[nx][ny] = 1; //表示访问过了 
				}
			} 
			 
		} 
	}
    return false; 
}
int check(int mid){ 
	memset(vis, 0, sizeof vis); //对vis数组 全部赋值 为0  表示没有访问过
	bool ans = false;
	for(int i = 1; i <= m; i++){
		ans = ans || BFS(2, i, mid);  //第1行是初始行 全部为0 所以从第2行开始BFS 
	} 
	return ans;
}
int main(){
	cin >> n >> m;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			cin >> a[i][j];
		}
	}
	int l = 1, r = 1005;
	while(l <= r){
		int mid = (l + r) >> 1;
		if(!check(mid)){    //思考一下返回的是什么 不要光想着套模板！！ 
			l = mid + 1;
		}
		else{
			r = mid - 1;
		}
	}
	cout << l;
	return 0;
}

整数域二分

洛谷 P1577 切绳子

有一个问题就是如果答案结果是1.99

与2.00进行相减判断 但是不通过 因为二进制表示的问题，0.1无法用二进制精确表示，所以在二进制相减中可能存在问题

Specual Judge问题，不用太在意格式 因为最终的评判标准时是与标准值作差 然后进行评判的 一般说保留三位 但是要考虑精度问题 尽量保留5位

转换方法：将小数转化到整数 先扩大 后结果缩小

实数域二分

P1570 KC 喝咖啡

P1678 烦恼的高考志愿

0x11 贪心法（Greedy）*

导言

找零问题：

每一步的判断是当前的最优选择，但是需要思考局部最优能否达到全局最优的问题

局部最优代替整体最优，其最终结果近似最优解

有点像背包问题啊

给个例子：

xi = {1, 5, 10, 20, 50, 100}

y = $$\sum w_i{x}_i$$

求min$$\sum w_i$$

可行解：问题给定一些约束条件，可以满足

最优解：

通过分步决策的方法，每一步决策产生一个向量

流程：

1. 存在可能解的集合

背包问题

0/1 背包问题

物体不能分割 只有两种状态 装入或者不装

一般背包问题

物体可分割，可以把物体x的xi部分装入到背包中

贪心思路：

1. 价值最大
2. 重量最轻
3. 单位重量价值最大

方案一：按物体价值降序装包

方案二：按物品重量非降序装包

方案三：按物体价值与重量比值的降序装包 先装最大的

活动安排问题

按结束的时间进行排列

最佳合并模式

类似于哈夫曼树

0x12 数论

质数

快速幂

$$(a^b)modn$$

快速幂就是解决上述问题

算法的思想是：分治

区分一下分治和二分的区别：

二分是舍弃掉一半，而分治是不断划分 然后合而治之

模板：

递归代码：

int quickPow(int a, int b){
    if(b == 1) return a;
    if(b % 2 == 0){
        int t = quickPow(a, b/2);
        return t * t % mod;
    }
    else{
        int t = quickPow(a, b/2);
        t = t * t % mod;
        t = t * a % mod;
        return t;
    }
}

非递归代码1：

int quickPow(int a, int b){
    int t = 
}

补充：

while(b){
    b = b / 2;
}

该式的时间复杂度为log n 级别的

例题：P1226

例题2：

数列求值

矩阵快速幂

单位矩阵：主对角线上的元素都是1

void matrixMulti(){
    for(int i = 1; i <= m; i++){
        for(int)
    }
}

最关键的地方：

不是矩阵乘幂的计算，而是如何得到一个可以用来形成乘幂计算的矩阵

$$\begin{gathered} S_n=1\ast S_{n-1}+1\ast f_n+0\ast f_{n-1} \\ {f}_{n+1}=0\ast S_{n-1}+1\ast f_n+1\ast f_{n-1} \\ {f}_n=0\ast S_{n-1}+1\ast f_n+0\ast f_{n-1} \end{gathered}$$

约数

求N的正约数集合：

• 试除法
• 倍数法

最大公约数和最小公倍数 P1029

扩欧算法

贝祖定理（斐蜀定理）

0x13 图论

基本概念

无向图和有向图的连通性

割点：去掉这个点之后 剩下的图不连通 那么这个点就是割点

割边：

双连通问题：

0x14 回溯法*

基本概念

需要找出问题的最优解 在一定的约束下进行，使用回溯法

设置一个目标函数，用来衡量每一个可能解的情况

搜索：

1. 以深度优先方式搜索解空间
2. 在搜索过程中使用剪枝函数，避免无效搜索

常用剪枝函数： 舍得！不行的就放弃 别挣扎

1. 用约束函数在扩展结点处减去不满足约束的子树 （不满足不可行）
2. 用限界函数剪去得不到最优解的字数 （可行但不最优）

涂色问题

前提：

• 不是优化问题，没有限界函数
• 搜索策略：深度优先
• 约束条件：相邻结点，不同颜色

4/n-皇后问题

解向量 ：
$$(x_1,x_2,...,x_n)$$
注意这个写法 直接限制了每一行只能放一个

设置约束条件：

限制列：i != j

限制对角线：

程序：

bool Place(int k, int i, int* ){
    for()
}

0/1背包问题

0x15 分支限界法*

4-皇后问题

广度优先

//结构体模板
template <class T>
struct Node{
    T cost;
    Node* parent;
}

Node<int> t;  //创建结构体 意味着上面模板中的T为int

注意上下界问题

0x16 优先队列