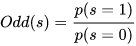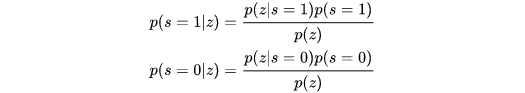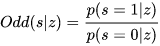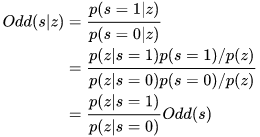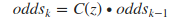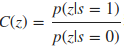Occupancy Grid Map
占用栅格的数据结构

cartographer 源码中实际上提供grid map两种形式，一种为probability，另一种为tsdf。由于建图默认配置为probability，同时也是slam中最为熟悉的。因此仅分析probability 类型的grid map。

grid map

cartographer中定义了一个基类Grid2D，而匹配使用的ProbabilityGrid则为继承。Grid2D描述了地图具体形式和存储内容。其内部成员如下：

  // 地图大小边界，包括x和y最大值， 分辨率， x和yu方向栅格数
  MapLimits limits_;
  //grid 地图存储值，采用uint16类型，
  std::vector<uint16> correspondence_cost_cells_;
  // 对应实际意义的最大和最小边界
  float min_correspondence_cost_;
  float max_correspondence_cost_;
  // 记录已经更新过的索引
  std::vector<int> update_indices_;

  // 已知栅格状态的大小
  Eigen::AlignedBox2i known_cells_box_;
  // 此为查询表格，主要因为grid存储的uint16格式，可根据此表格将其对应成实际意义的如probability
  const std::vector<float>* value_to_correspondence_cost_table_;

grid2d作为基类，存储单元为uint16整型数，即0~65535，而不关心具体实际意义。其目的是方便代码复用，即建立不同的继承类。可通过value_to_correspondence_cost_table_表格进行还原真实表示意义。采用整数进行存储，其好处无需解释。而且此类中函数主要用于设置和访问的。
其中GrowLimits用于扩展此gridmap的大小，即当加入一个已知栅格状态时，需要判断并扩展当前gridmap。

// 更新地图大小，同时将原grid中数据按照位置放入新放大的grid中
void Grid2D::GrowLimits(const Eigen::Vector2f& point,
                        const std::vector<std::vector<uint16>*>& grids,
                        const std::vector<uint16>& grids_unknown_cell_values) {
  CHECK(update_indices_.empty());
  //如果当前的存在point不在范围内，即需要更新，采用迭代方法放大地图边界，
  while (!limits_.Contains(limits_.GetCellIndex(point))) {
    //获取原来的地图大小的中心坐标，即栅格索引
    const int x_offset = limits_.cell_limits().num_x_cells / 2;
    const int y_offset = limits_.cell_limits().num_y_cells / 2;
    // grid最大值更新原来的一半， 地图总大小放大一倍。 即从地图中心位置上下左右均放大原大小一半
    const MapLimits new_limits(
        limits_.resolution(),
        limits_.max() +
            limits_.resolution() * Eigen::Vector2d(y_offset, x_offset),
        CellLimits(2 * limits_.cell_limits().num_x_cells,
                   2 * limits_.cell_limits().num_y_cells));
    // 行数，用于转换1维索引
    const int stride = new_limits.cell_limits().num_x_cells;
    //新的offset
    const int offset = x_offset + stride * y_offset;
    //新大小
    const int new_size = new_limits.cell_limits().num_x_cells *
                         new_limits.cell_limits().num_y_cells;

    //更新grid概率，即将原来的概率赋值在新的grid中
    for (size_t grid_index = 0; grid_index < grids.size(); ++grid_index) {
      std::vector<uint16> new_cells(new_size,
                                    grids_unknown_cell_values[grid_index]);
      for (int i = 0; i < limits_.cell_limits().num_y_cells; ++i) {
        for (int j = 0; j < limits_.cell_limits().num_x_cells; ++j) {
          new_cells[offset + j + i * stride] =
              (*grids[grid_index])[j + i * limits_.cell_limits().num_x_cells];
        }
      }
      *grids[grid_index] = new_cells;
    }
    limits_ = new_limits;
    // 重新计算有效栅格空间边界，即由于起点发生改变，则矩形框的坐标需进行转换
    if (!known_cells_box_.isEmpty()) {
      known_cells_box_.translate(Eigen::Vector2i(x_offset, y_offset));
    }
  }
}

probability map

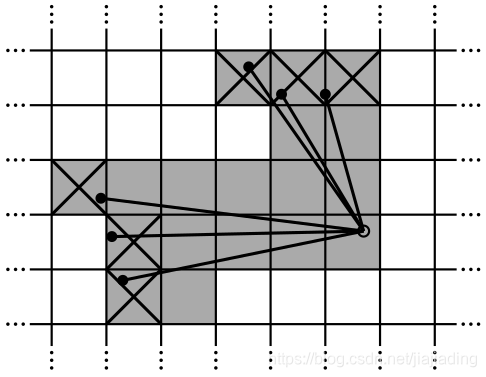
ProbabilityGrid是继承Grid2D，实际是具体描述了Grid2D单元存储内容的具体意义，即为概率。根据栅格地图基本原理可知，一个单元格最终想表示的障碍物是否存在，即三个状态：占有（hit），未占有（miss），未知。如原论文中激光光束模型，其中白色格表示未知状态，X表示占有，灰色表示free。但由于传感器噪声和栅格分辨率的问题，因此状态不会为确定值。因此我们将其以概率形式表示，包括占有概率和未占有概率。

代码目录cartographer/map/probability_values.h中定义了probability中单元格表示意义的转换关系。

// 概率用odd模型表示
inline float Odds(float probability) {
  return probability / (1.f - probability);
}

//odd 转换为概率模型
inline float ProbabilityFromOdds(const float odds) {
  return odds / (odds + 1.f);
}

// hit概率转换为free概率
inline float ProbabilityToCorrespondenceCost(const float probability) {
  return 1.f - probability;
}
// free概率转换为hit概率
inline float CorrespondenceCostToProbability(const float correspondence_cost) {
  return 1.f - correspondence_cost;
}

// 概率空间范围限制，默认0.1~0.9
constexpr float kMinProbability = 0.1f;
constexpr float kMaxProbability = 1.f - kMinProbability;
constexpr float kMinCorrespondenceCost = 1.f - kMaxProbability;
constexpr float kMaxCorrespondenceCost = 1.f - kMinProbability;

前面Grid2D基类也提过每个单元存储的为uint16的的整数，因此probability_values.h文件中也将对应概率值转换为1~32767之间，而0表示未知状态。

// Converts a correspondence_cost to a uint16 in the [1, 32767] range.
inline uint16 CorrespondenceCostToValue(const float correspondence_cost) {
  return BoundedFloatToValue(correspondence_cost, kMinCorrespondenceCost,
                             kMaxCorrespondenceCost);
}

// Converts a probability to a uint16 in the [1, 32767] range.
inline uint16 ProbabilityToValue(const float probability) {
  return BoundedFloatToValue(probability, kMinProbability, kMaxProbability);

// 具体转换公式
inline uint16 BoundedFloatToValue(const float float_value,
                                  const float lower_bound,
                                  const float upper_bound) {
  const int value =
      common::RoundToInt(
          (common::Clamp(float_value, lower_bound, upper_bound) - lower_bound) *
          (32766.f / (upper_bound - lower_bound))) +
      1;
  // DCHECK for performance.
  DCHECK_GE(value, 1);
  DCHECK_LE(value, 32767);
  return value;
}

当然也包括value转换回hit概率和miss概率，即probability_values.h中定义了所有数据类型之间的转换函数，以及边界和数据的意义。

probability map cell 初始化

概率栅格图初始化即设置grid格的probability和获取对应的probability，其代码实现在cartographer/mapping/2d/probability_grid.c中。SetProbability表示的是在对应坐标下的grid cell设置其概率值。

// 设置对应index的概率值， 在cell单元存储的则是概率对应的free 占有率， 对应的uint16整形数
void ProbabilityGrid::SetProbability(const Eigen::Array2i& cell_index,
                                     const float probability) {
  // 取cell_index在栅格地图中对应索引的单元的地址
  // ToFlatIndex, 二维坐标转换为1维索引
  // mutable_correspondence_cost_cells() 返回的grid中grid地图
  uint16& cell =
      (*mutable_correspondence_cost_cells())[ToFlatIndex(cell_index)];
  CHECK_EQ(cell, kUnknownProbabilityValue);
  // 将概率值转换对应的整型数，然后存入对应的索引的单元中
  cell =
      CorrespondenceCostToValue(ProbabilityToCorrespondenceCost(probability));

  // 返回的是有效概率值的矩形框，每更新一个cell， 则更新矩形框box， 采用eigen库extend，自动更新有效框
  mutable_known_cells_box()->extend(cell_index.matrix());
}

通过以上代码分析可看出，由于初始化操作，即该单元为第一次赋值，而非更新，即需要判断当前cell是否未知状态，如果不是未知状态，则不能初始化，而是更新（下面会详细讲解）。同时可以看出cartographer的概率grid cell实际存储的是free probability对应的value值，即为空闲概率。

// Returns the probability of the cell with 'cell_index'.
// 返回对应的index的占有概率值
float ProbabilityGrid::GetProbability(const Eigen::Array2i& cell_index) const {
  if (!limits().Contains(cell_index)) return kMinProbability;
  return CorrespondenceCostToProbability(ValueToCorrespondenceCost(
      correspondence_cost_cells()[ToFlatIndex(cell_index)]));
}

以上代码则是从grid 中取出对应坐标位置的占有概率。为何要存储free概率，而设置和获取均为hit概率，为何中间多一个转换步骤，反而是多此一举，其实前3节前端匹配已有体现，主要是匹配操作时采用类似最小二乘的优化思想，需要将最佳匹配值改为求取最小状态，因此采取free的概率进行匹配，则最小值则为最佳匹配。

probability grid地图更新

在占据栅格地图中，对于一个点，我们用p(s=0)来表示它是Free状态的概率，用p(s=1)来表示它是Occupied状态的概率，两者的和为1。我们希望一个栅格中仅有一个值，因此引入两者的比值来作为此cell的状态：

对于一个cell，如果新观察到一个值z，由于z只能为1和0即要不hit，要不miss，然后根据观测值z我们需要更新它的状态。因此其观测的更新概率可以看做为p(s=1|z)和p(s=0|z)。即在当前观测z（占hit或misss）的情况下，一个栅格实际为hit的概率和miss的概率，即为条件概率。因此可以用贝叶斯公式进行求取，如下：

现在假设原来cell为odd(s)， 而对应的更新odd则为

根据贝叶斯公式进行代入可获取如下公式：

如此可清晰看出更新后的cell应为

其中k-1为上一时刻的odds，而k为经过一次观测后的odds，显然仅是相差了C(z)这个系数。由于栅格表示是否为障碍物，观测采用激光测距是否障碍，显然仅有是（hit）和不是（miss）两种状态。其中系数为
其中p(z|s=1)表示的是当cell为障碍时，即z=1，传感器认为是障碍的概率，显然是传感器本身属性决定的，因此为一常数。同样其他3种组合也均为常数，因此其系数C(z)是根据观测hit和miss决定的两个常数，即C_miss 和C_hit 两个常数。

简单总结:其更新过程可认为根据传感器观测的状态，对原cell的概率进行更新，假设原cell的值为value。当传感器测到此cell为hit时，则新的value_new=C_hit * value; 如果传感器测的此cell为miss时，则新的value_new=C_miss * value