2025CSP-J 冲刺训练 1
距
C
S
P
−
J
/
S
2025
\tt CSP-J/S 2025
CSP−J/S2025 第一轮 还剩
244
\tt 244
244 天
距
C
S
P
−
J
/
S
2025
\tt CSP-J/S 2025
CSP−J/S2025 第二轮 还剩
279
\tt 279
279 天
一、基础知识
1. 加法原理
加法原理的核心思想:如果一个问题可以分解成互不相交的多个子问题,那么问题的总数目等于各个子问题的数目之和。
2. 乘法原理
乘法原理的核心思想:如果一个过程可以分为 n n n 个独立的步骤,其中第 i i i 个步骤有 m i m_i mi 种选择方式,那么整个过程的选择方式数目为 m 1 × m 2 × ⋯ × m n m_1 × m_2 × \cdots × m_n m1×m2×⋯×mn。
3. 排列数
A
n
m
A_n^m
Anm(
P
n
m
P_n^m
Pnm)表示排列数,计算方法为从
n
n
n 向下数连续的
m
m
m 个数累乘,即:
A
n
m
=
n
!
m
!
=
n
×
(
n
−
1
)
×
(
n
−
2
)
×
⋯
×
(
n
−
m
+
1
)
A_n^m=\frac{n!}{m!}=n\times (n-1)\times(n-2)\times\cdots\times(n-m+1)
Anm=m!n!=n×(n−1)×(n−2)×⋯×(n−m+1)
4. 组合数
C
n
m
C_n^m
Cnm 表示组合数,计算方法为
A
n
m
A_n^m
Anm 的基础上除以
m
m
m 个数排列的次数(
A
m
m
A_m^m
Amm),即:
C
n
m
=
A
n
m
A
m
m
=
A
n
m
m
!
=
n
×
(
n
−
1
)
×
(
n
−
2
)
×
⋯
×
(
n
−
m
+
1
)
m
×
(
m
−
1
)
×
(
m
−
2
)
×
⋯
×
1
C_n^m=\frac{A_n^m}{A_m^m}=\frac{A_n^m}{m!}=\frac{n\times(n-1)\times(n-2)\times\cdots\times(n-m+1)}{m\times(m-1)\times(m-2)\times\cdots\times1}
Cnm=AmmAnm=m!Anm=m×(m−1)×(m−2)×⋯×1n×(n−1)×(n−2)×⋯×(n−m+1)
二、模板
1. 快速幂
typedef long long ll;
const ll MOD=1e9+7;
ll qpow(ll a,ll b){
ll ret=1;
a%=MOD;
while(b){
if(b&1)//if(b%2==1)
ret=(ret*a)%MOD;
a=(a*a)%MOD;
b>>=1;//b/=2
}
return ret;
}
2. 组合数预处理
for(int i=0;i<MAXN;i++){//组合数预处理
comb[i][0]=1;
for(int j=1;j<i;j++)
comb[i][j]=(comb[i-1][j]+comb[i-1][j-1])%MOD;
comb[i][i]=1;
}
三、基础例题
1. 涂色
1.1 审题
题目描述
有排成一列的 N N N 个球。现在小明想要把这些球都涂成 K K K 种颜色中的某一种。若要求任意相邻两个球颜色不同,共有多少种不同的涂色方法?答案可能很大,你只需要输出答案除以 1 0 9 + 7 10^9+7 109+7 的余数。
输入描述
一行,两个正整数 N , K N,K N,K。
输出描述
一行,一个整数代表涂色方法数除以 1 0 9 + 7 10^9+7 109+7 的余数。
样例1
输入
2 2输出
2
样例2
输入
10 8输出
322828856
提示
1 ≤ N ≤ 1 0 3 1\le N\le10^3 1≤N≤103, 2 ≤ K ≤ 1 0 3 2\le K\le10^3 2≤K≤103。
1.2 分析
首先,我们考虑球的涂色方式。第一个球有 k k k 种颜色可以选择,第二个球就只能选择 k − 1 k-1 k−1 种颜色(因为要求相邻两个球颜色不同)。同理,第三个球只能选择 k − 1 k-1 k−1 种颜色,以此类推。
因此,总的涂色方式就是将每个球的涂色方式相乘。第一个球有 k k k 种选择,第二个球有 k − 1 k-1 k−1 种选择,以此类推。所以总的涂色方式为 k × ( k − 1 ) × ( k − 1 ) × ⋯ × ( k − 1 ) k\times(k-1)\times(k-1)\times\cdots\times(k-1) k×(k−1)×(k−1)×⋯×(k−1),其中一共有 n − 1 n-1 n−1 个 ( k − 1 ) (k-1) (k−1) 相乘。
1.3 参考答案
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD=1e9+7;
int n,k;
ll qpow(ll a,ll b){
ll ret=1;
a%=MOD;
while(b){
if(b&1)//if(b%2==1)
ret=(ret*a)%MOD;
a=(a*a)%MOD;
b>>=1;//b/=2
}
return ret;
}
int main(){
cin>>n>>k;
cout<<k*qpow(k-1,n-1)%MOD;
return 0;
}
2. 计数1
2.1 审题
题目描述
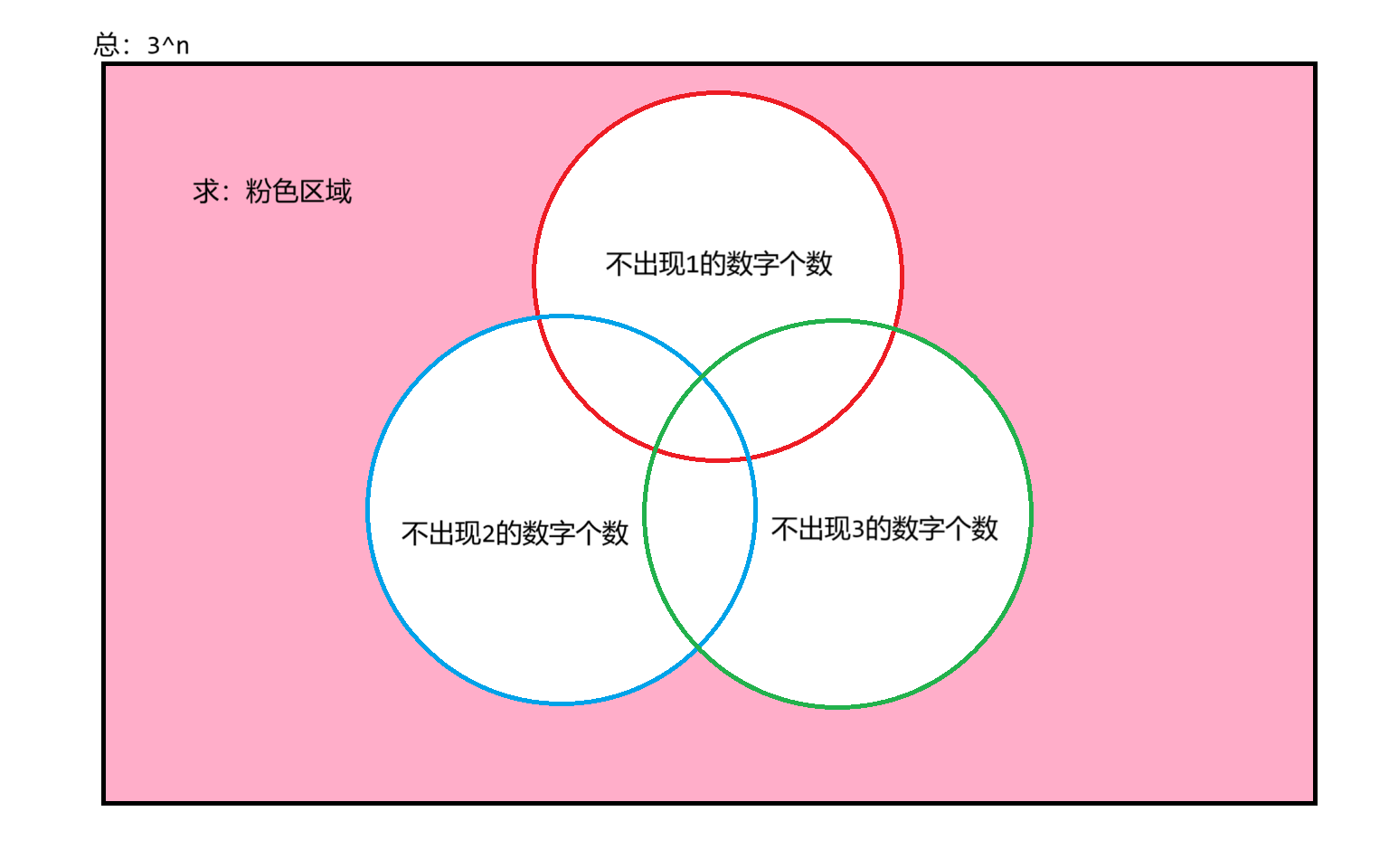
由数字 1 , 2 , 3 1,2,3 1,2,3 组成的 n n n 位数,要求 n n n 位数中 1 , 2 , 3 1,2,3 1,2,3 的每一个至少出现一次。求所有这种 n n n 位数的个数。
答案可能很大,你只需要输出答案除以 1 0 9 + 7 10^9+7 109+7 的余数。
输入描述
一个整数 n n n。
输出描述
输出答案除以 1 0 9 + 7 10^9+7 109+7 的余数。
样例1
输入
3输出
6
样例2
输入
2输出
0
样例3
输入
199997输出
837597358
提示
80 % 80\% 80% 数据: 1 ≤ n ≤ 1 0 6 1\le n\le10^6 1≤n≤106。
100 % 100\% 100% 数据: 1 ≤ n ≤ 1 0 9 1\le n\le10^9 1≤n≤109。
2.2 分析
我们可以画出下面的一张图,利用三个集合的容斥原理完成这道题目。
2.3 参考答案
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD=1e9+7;
int n,ans;
ll qpow(ll a,ll b){
ll ret=1;
a%=MOD;
while(b){
if(b&1)//if(b%2==1)
ret=(ret*a)%MOD;
a=(a*a)%MOD;
b>>=1;//b/=2
}
return ret;
}
int main(){
cin>>n;
ll u=qpow(3,n),C1=qpow(2,n),C1U2=1,C1U2U3=0;
cout<<((u-(3*C1-3*C1U2+C1U2U3))%MOD+MOD)%MOD;
return 0;
}
3. 组合数预处理
3.1 审题
杨辉三角是一类非常有趣的数阵,最外层的数值均为
1
1
1,中间的数值则为正上方和左上角的两个数值相加。杨辉三角内的数就是组合数,
n
n
n 层杨辉三角就可以用来计算所有
i
<
n
i<n
i<n 的组合数
C
i
j
C_i^j
Cij。
读入一个正整数
n
n
n,请编程打印一个
n
n
n 行的杨辉三角。杨辉三角中的数会很大,你只需要输出它们除以
1
0
9
+
7
10^9+7
109+7 的余数。
3.2 分析
需要掌握一个公式【不是本题的,给大家拓展一下信息学很常见的公式】:
∑
i
=
0
n
C
n
i
=
2
n
\sum_{i=0}^{n}C_n^i=2^n
i=0∑nCni=2n
根据二项式定理:
(
a
+
b
)
n
=
∑
i
=
0
n
C
n
i
a
n
−
i
b
i
(a + b)^n = \sum_{i=0}^{n} C_n^i a^{n-i} b^i
(a+b)n=i=0∑nCnian−ibi
这个等式是对任意的实数a和b都成立的。当我们令
a
=
1
,
b
=
1
a = 1,b = 1
a=1,b=1 时,可以得到特定的形式:
(
1
+
1
)
n
=
∑
i
=
0
n
C
n
i
(1 + 1)^n = \sum_{i=0}^{n} C_n^i
(1+1)n=i=0∑nCni
特别地,这个等式的左边是非常简单的,即
2
n
2^n
2n。所以我们可以通过令
a
=
1
,
b
=
1
a = 1,b = 1
a=1,b=1,简化等式,从而得到:
∑
i
=
0
n
C
n
i
=
2
n
\sum_{i=0}^{n} C_n^i = 2^n
i=0∑nCni=2n
3.3 参考答案
水法:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=2e3+8;
const ll MOD=1e9+7;
ll n,a[MAXN][MAXN];
int main(){
cin>>n;
a[1][1]=1,a[2][1]=1,a[2][2]=1;
for(int i=3;i<=n;i++)
for(int j=1;j<=i;j++)
a[i][j]=(a[i-1][j]+a[i-1][j-1])%MOD;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
cout<<a[i][j]<<" \n"[j==i];
return 0;
}
标准:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=2e3+8;
const ll MOD=1e9+7;
ll n,comb[MAXN][MAXN];
int main(){
for(int i=0;i<MAXN;i++){//组合数预处理
comb[i][0]=1;
for(int j=1;j<=i;j++)
comb[i][j]=(comb[i-1][j]+comb[i-1][j-1])%MOD;
}
cin>>n;
for(ll i=0;i<n;i++)
for(ll j=0;j<=i;j++)
cout<<comb[i][j]<<" \n"[j==i];
return 0;
}
四、例题
## 1. 计数2
1.1 审题
农夫约翰建造了一座有
n
n
n 间牛舍的小屋,牛舍排在一条直线上,从左到右编号为
1
∼
n
1\sim n
1∼n。
但是约翰的
m
m
m 头牛对小屋很不满意,只要有两头牛之间的牛舍数量小于
k
k
k,他们就会互相攻击。住在同一间牛舍更是不行。
约翰为了防止牛之间互相攻击,有多少种安排牛入住牛舍的方法?答案可能很大,你只需要输出答案除以
1
0
9
+
7
10^9+7
109+7 的余数。
1.2 分析
首先,有 m m m 头牛和 n n n 个牛舍,每头牛可以选择一个牛舍入住。我们可以将问题分成两部分考虑:
- 选择 m m m 个不同的牛舍供 m m m 头牛入住。
- 将剩余的 n − k × ( m − 1 ) n - k\times(m-1) n−k×(m−1) 个牛舍分配给 ( m − 1 ) (m-1) (m−1) 头牛。
对于第一部分,我们需要从 n n n 个牛舍中选择 m m m 个不同的牛舍供 m m m 头牛入住,这可以表示为组合数 C n m C_{n}^{m} Cnm。
对于第二部分,我们需要将剩余的 n − k × ( m − 1 ) n - k\times(m-1) n−k×(m−1) 个牛舍分配给 ( m − 1 ) (m-1) (m−1) 头牛。这相当于将 n − k × ( m − 1 ) n - k\times(m-1) n−k×(m−1) 个牛舍分成 ( m − 1 ) (m-1) (m−1) 组,每组至少有 k k k 个牛舍。这可以表示为组合数 C n − k × ( m − 1 ) m − 1 C_{n-k\times(m-1)}^{m-1} Cn−k×(m−1)m−1。
综上所述,有 m m m 头牛和 n n n 个牛舍的安排方法数量为 C n m × C n − k × ( m − 1 ) m − 1 C_{n}^{m} \times C_{n-k\times(m-1)}^{m-1} Cnm×Cn−k×(m−1)m−1。
我们可以利用组合数的性质,即 C n m = C n n − m C_{n}^{m} = C_{n}^{n-m} Cnm=Cnn−m,将上述公式转化为 C n m × C n − k × ( m − 1 ) m − 1 = C n m × C n − k × ( m − 1 ) n − k × ( m − 1 ) − ( m − 1 ) C_{n}^{m} \times C_{n-k\times(m-1)}^{m-1} = C_{n}^{m} \times C_{n-k\times(m-1)}^{n-k\times(m-1)-(m-1)} Cnm×Cn−k×(m−1)m−1=Cnm×Cn−k×(m−1)n−k×(m−1)−(m−1)。
由于题目中要求的是将 n n n 个牛舍分成 m m m 组,每组至少有k个牛舍的安排方法数量,所以我们可以得到公式 C n − k × ( m − 1 ) m = C n m × C n − k × ( m − 1 ) n − k × ( m − 1 ) − ( m − 1 ) C_{n-k\times(m-1)}^{m} = C_{n}^{m} \times C_{n-k\times(m-1)}^{n-k\times(m-1)-(m-1)} Cn−k×(m−1)m=Cnm×Cn−k×(m−1)n−k×(m−1)−(m−1)。
注意:这里使用的组合数公式是基于组合数的性质 C n m = C n n − m C_{n}^{m} = C_{n}^{n-m} Cnm=Cnn−m,并且假设 n n n 不小于 m m m。如果 n n n 小于 m m m,那么 C n m = 0 C_{n}^{m} = 0 Cnm=0。
1.3 参考答案
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=5e3+8;
const ll MOD=1e9+7;
ll n,m,k,comb[MAXN][MAXN];
int main(){
for(int i=0;i<MAXN;i++){//组合数预处理
comb[i][0]=1;
for(int j=1;j<i;j++)
comb[i][j]=(comb[i-1][j]+comb[i-1][j-1])%MOD;
comb[i][i]=1;
}
cin>>n>>m>>k;
if(n-k*(m-1)<0){
cout<<0;
return 0;
}
cout<<comb[n-k*(m-1)][m];
return 0;
}
2. 互不相等
2.1 审题
考虑一个长度为
n
n
n 的正整数数列
a
1
,
a
2
,
⋯
,
a
n
a_1,a_2,\cdots,a_n
a1,a2,⋯,an。满足如下条件:
(1)
1
≤
a
i
≤
c
i
1\le a_i\le c_i
1≤ai≤ci(
1
≤
i
≤
n
1\le i\le n
1≤i≤n)
(2)
a
i
≠
a
j
a_i\ne a_j
ai=aj(
1
≤
i
<
j
≤
n
1\le i<j\le n
1≤i<j≤n)
其中
c
1
,
c
2
,
⋯
,
c
n
c_1,c_2,\cdots,c_n
c1,c2,⋯,cn 是已知的正整数。你要求出有多少种不同的数列
a
a
a 满足条件。答案会很大,所以只需要输出答案除以
1
0
9
+
7
10^9+7
109+7 的余数。
2.2 分析
首先不难想到可以先进行排序,把小的先枚举了,然后依次乘大的。由于所有元素不能像等,所以后面的元素只有 c i − i + 1 c_i-i+1 ci−i+1 种选择。记得特判 < 0 <0 <0 的情况。
2.3 参考答案
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN=2e5+8;
const ll MOD=1e9+7;
ll n,c[MAXN],ans=1;
int main(){
cin>>n;
for(int i=1;i<=n;i++)
cin>>c[i];
sort(c+1,c+n+1);//先枚举小的
for(int i=1;i<=n;i++)
ans=(ans*(c[i]-i+1<0?0:c[i]-i+1))%MOD;
cout<<ans;
return 0;
}