Leetcode142. 环形链表 II(HOT100)

我的错误代码：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head||!head->next)return nullptr;
        ListNode* f = head->next,*s = head;
        while(f){
            f = f->next,s = s->next;
            if(!f)return nullptr;
            f = f->next;
            if(f==s){
                ListNode* newHead = head;
                ListNode* cur = s;
                while(cur!=newHead){
                    cur = cur->next;
                    newHead = newHead->next;
                }
                return cur;
            }
        }
        return nullptr;
    }
};

正确的代码：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head||!head->next)return nullptr;
        ListNode* f = head,*s = head;//not head->next!
        while(f){
            f = f->next,s = s->next;
            if(!f)return nullptr;
            f = f->next;
            if(f==s){
                ListNode* newHead = head;
                ListNode* cur = s;
                while(cur!=newHead){
                    cur = cur->next;
                    newHead = newHead->next;
                }
                return cur;
            }
        }
        return nullptr;
    }
};

或者：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head||!head->next)return nullptr;
        ListNode* f = head->next,*s = head;
        while(f){
            f = f->next,s = s->next;
            if(!f)return nullptr;
            f = f->next;
            if(f==s){
                ListNode* newHead = head;
                ListNode* cur = s->next;
                while(cur!=newHead){
                    cur = cur->next;
                    newHead = newHead->next;
                }
                return cur;
            }
        }
        return nullptr;
    }
};

错误原因：fast没有从head走（也就是没有从头走），导致newHead与cur相遇距离与预期不一致（本来我们计算好的是他俩相遇于环的起点，但是现在newHead与cur由于fast先走了一步导致newHead距离环入口差一步的时候，cur已经到了入口处），那么也就是说：两个距离为一的节点，且每次往前走一步，显然不可能相遇。即：newHead指针与cur永远不可能相遇。导致超时。

上道题是：环形链表，我们的快指针从head->next走，是可以的，一来人家没让计算入口地址，我们不用定义cur and newHead ,而来fast总是比slow快，所以必然相遇。

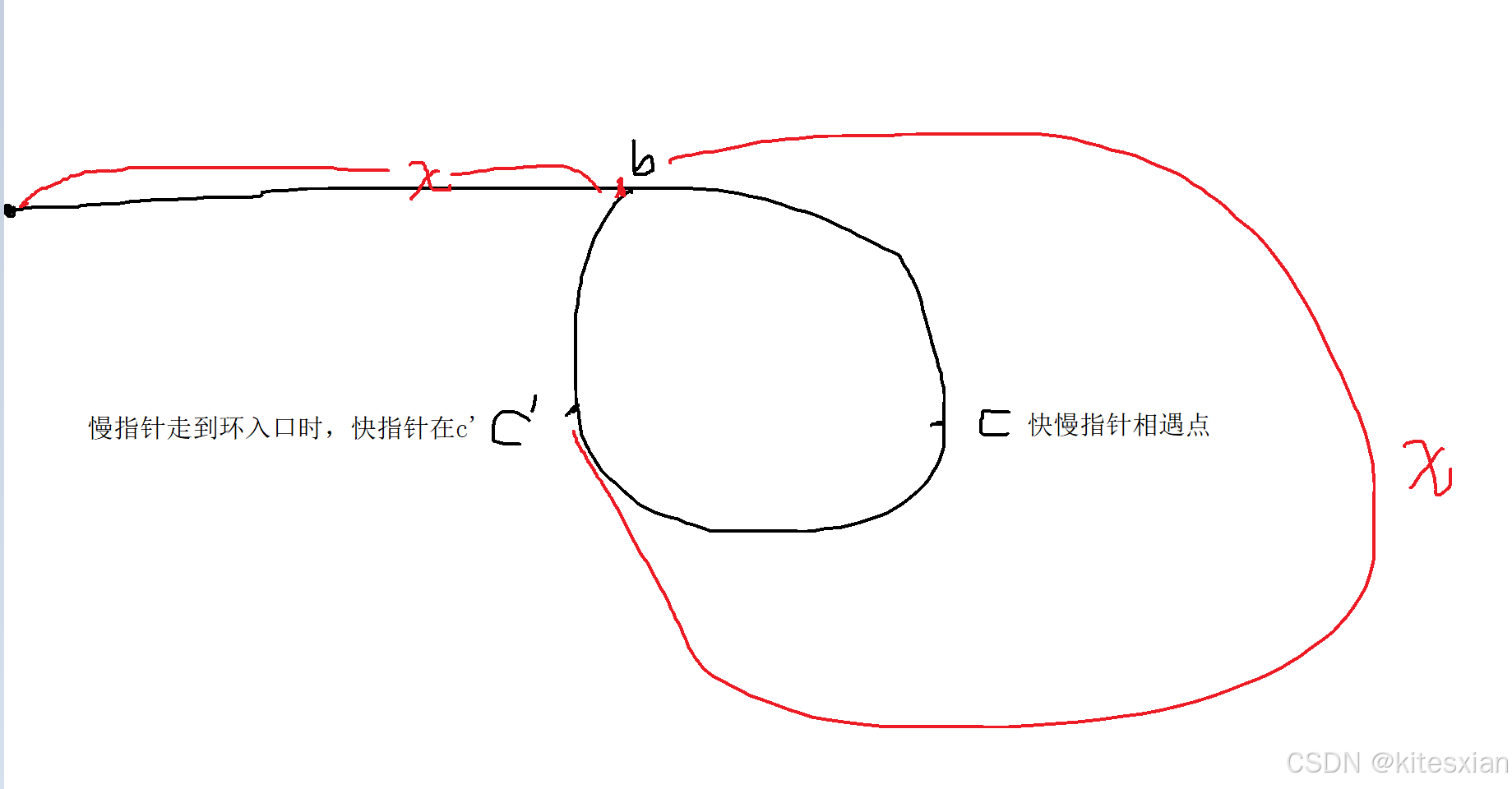
图解：

假设快慢指针相遇于c点，还假设慢指针初次到达环入口（b）时，快指针在c‘处。

当慢指针在b时，快指针在c’，然后后者以前者两倍的速度追赶，最终，慢指针从b->c，

快指针从c'-->b-->c，我们不难发现c'b的距离=bc的距离。

另外，我们还应该可以看出来b-->c-->c'的距离为x，也就是从起点到b的距离。

而由于c'b=bc，则bc'+c'c=x。

也就说：当一个指针从起点开始，另一个指针从c开始，两者每次一步，它们最终会相遇于b点，b点就是本题答案。

Leetcode142. 环形链表 II(HOT100)

悦读