闹海闹元宵！顶刊算法+分解组合+四模型对比！SGMD-FATA-Transformer-BiLSTM多变量时间序列预测

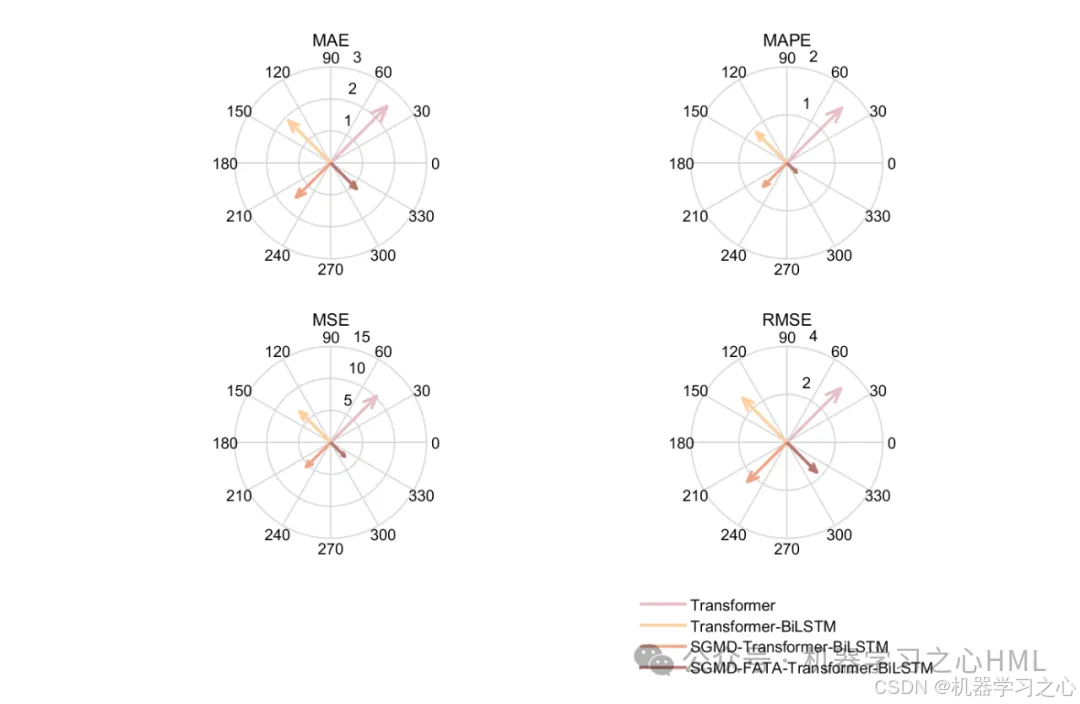
效果一览

在这里插入图片描述

基本介绍

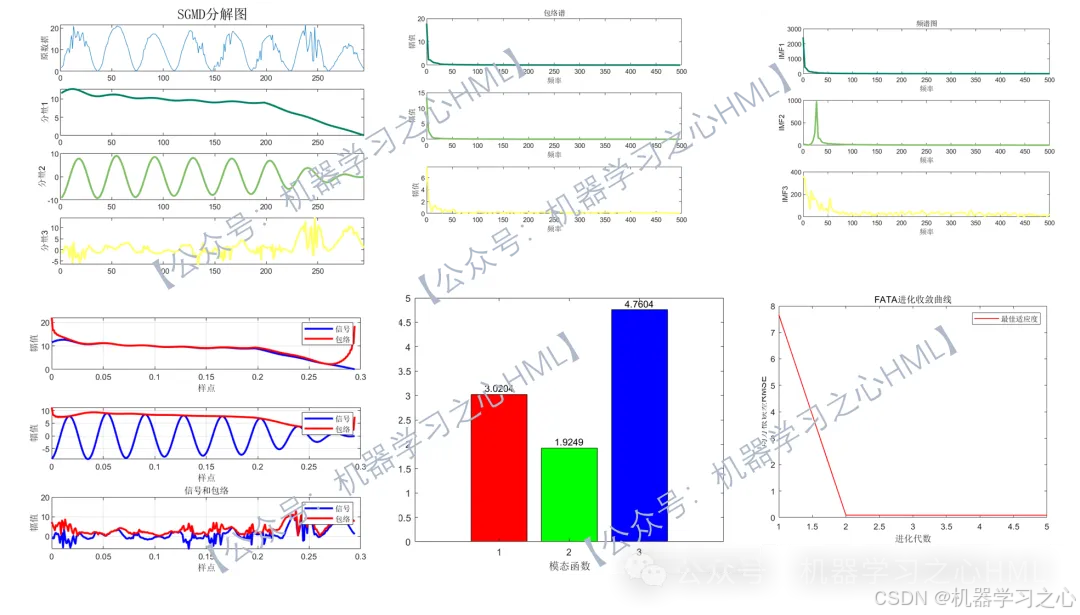
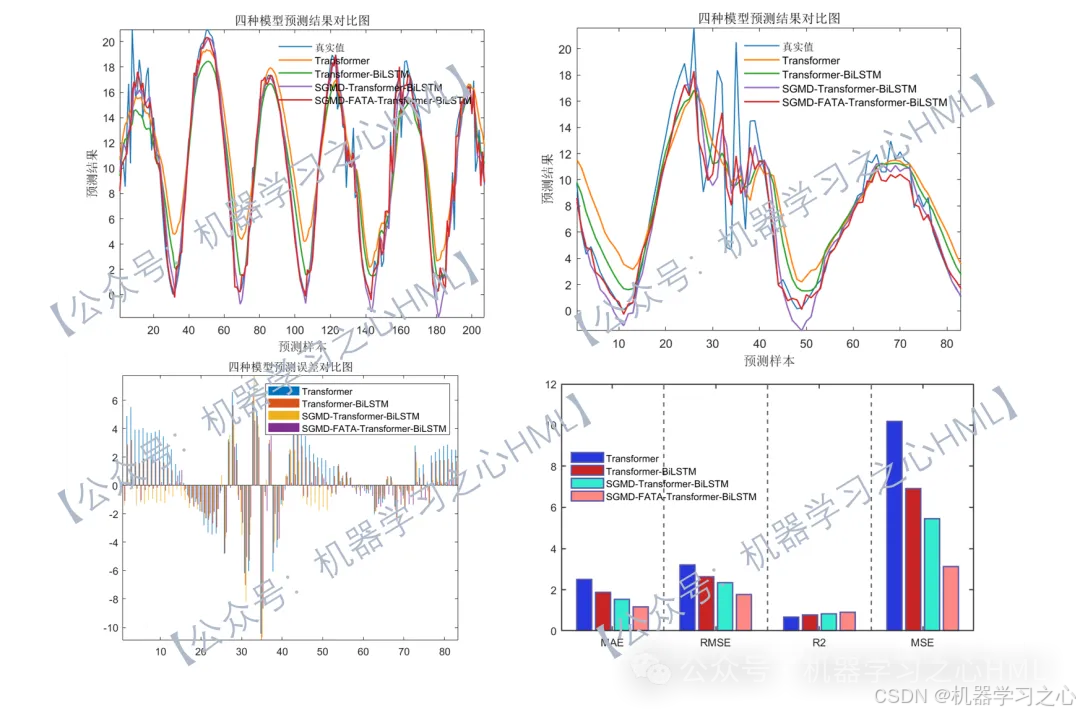
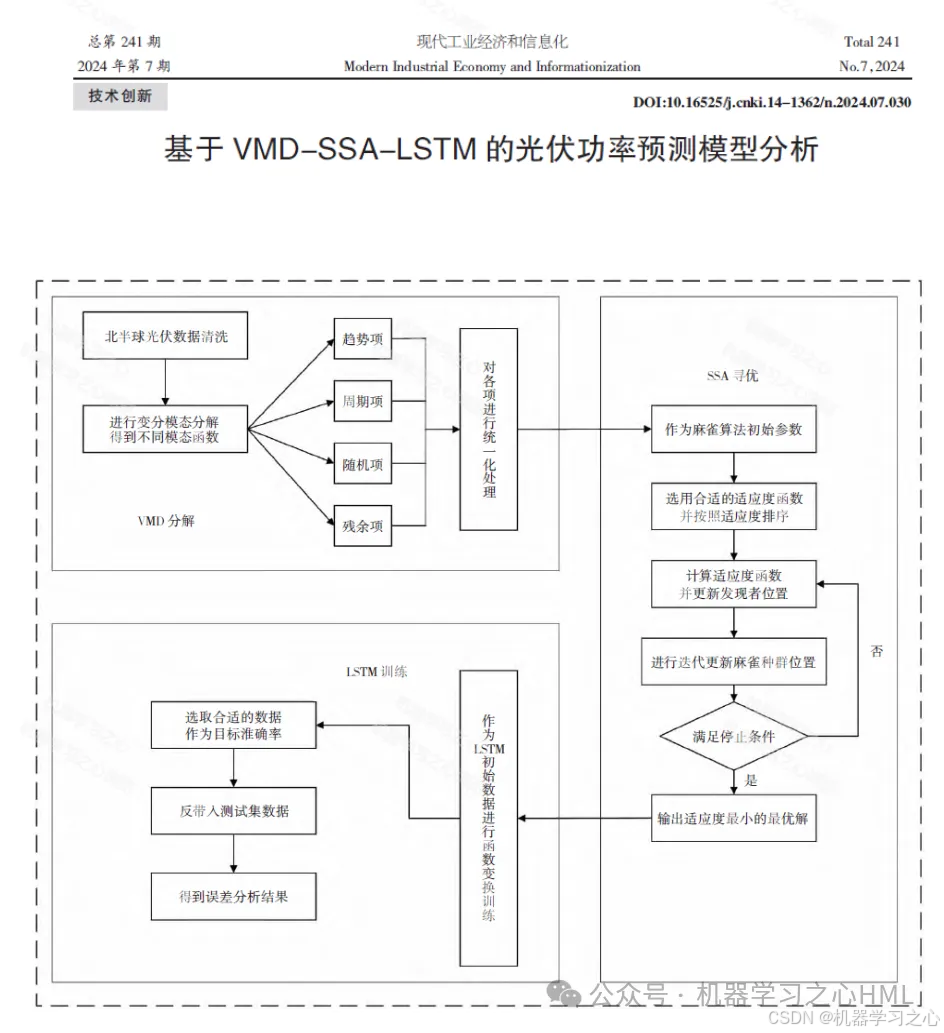
1.SCI算法海市蜃楼优化算法优化算法+分解组合对比！SGMD-FATA-Transformer-BiLSTM多变量时间序列光伏功率预测，辛几何模态分解+海市蜃楼优化算法优化Transformer结合双向长短期记忆神经网络多变量时间序列预测（程序可以作为核心级论文代码支撑，目前尚未发表）；
海市蜃楼优化算法(Fata morgana algorithm, FATA)是一种新型的元启发式算法（智能优化算法），灵感来源于海市蜃楼的形成过程，该成果由Ailiang Qi于2024年8月发表在SCI的Top期刊《Neurocomputing》上！
2.算法优化参数为：学习率，隐含层单元数目，最大训练周期，运行环境为Matlab2023b及以上；
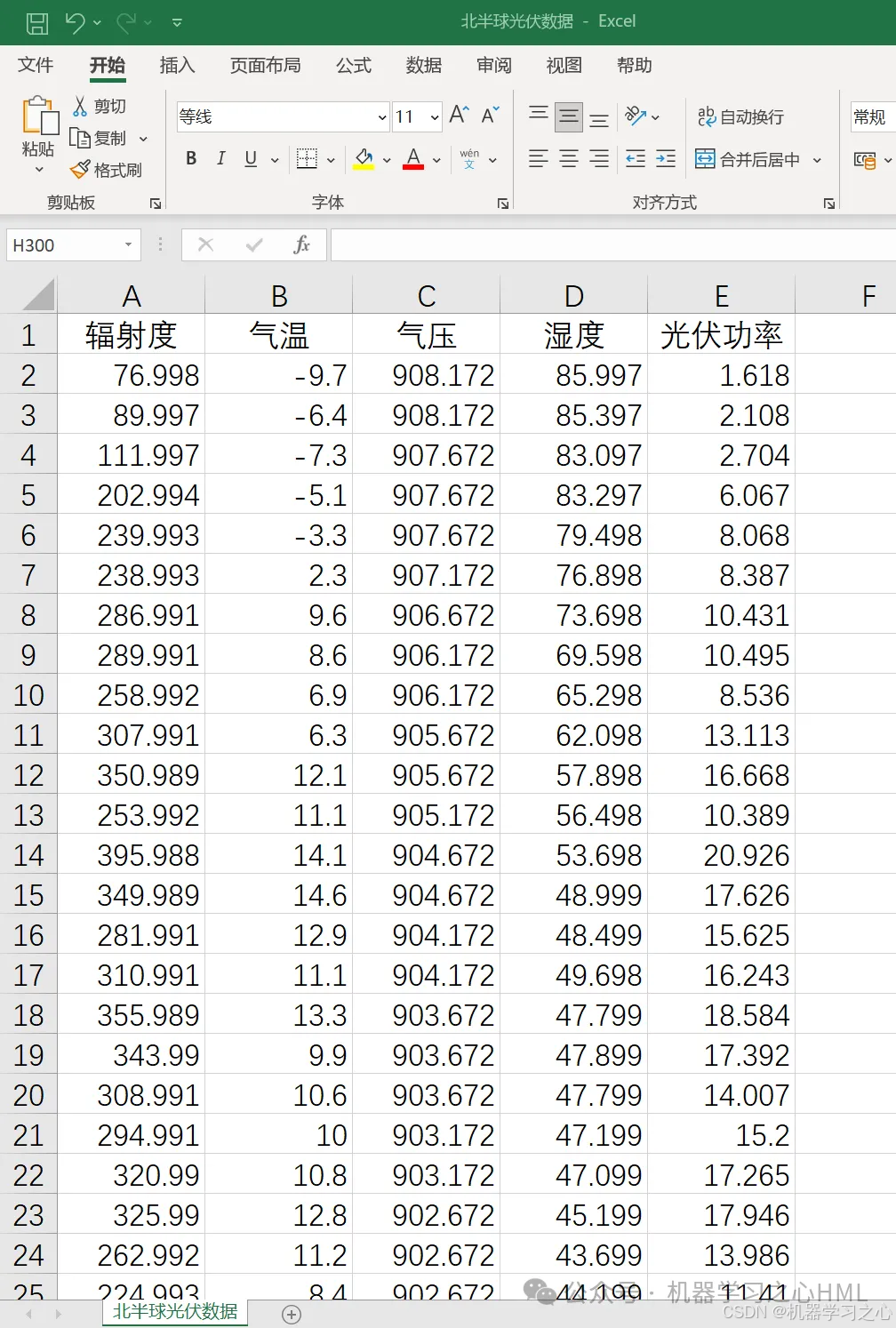
3.数据集为excel（光伏功率数据集，输入辐射度、气温、气压、湿度，输出光伏功率），输入多个特征，输出单个变量，考虑历史特征的影响，多变量时间序列预测，主程序运行即可，所有文件放在一个文件夹；
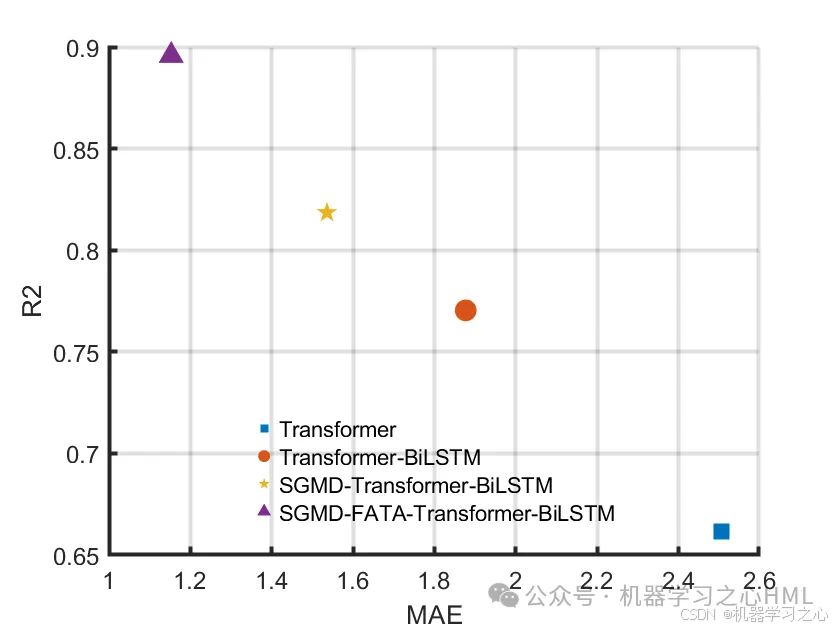
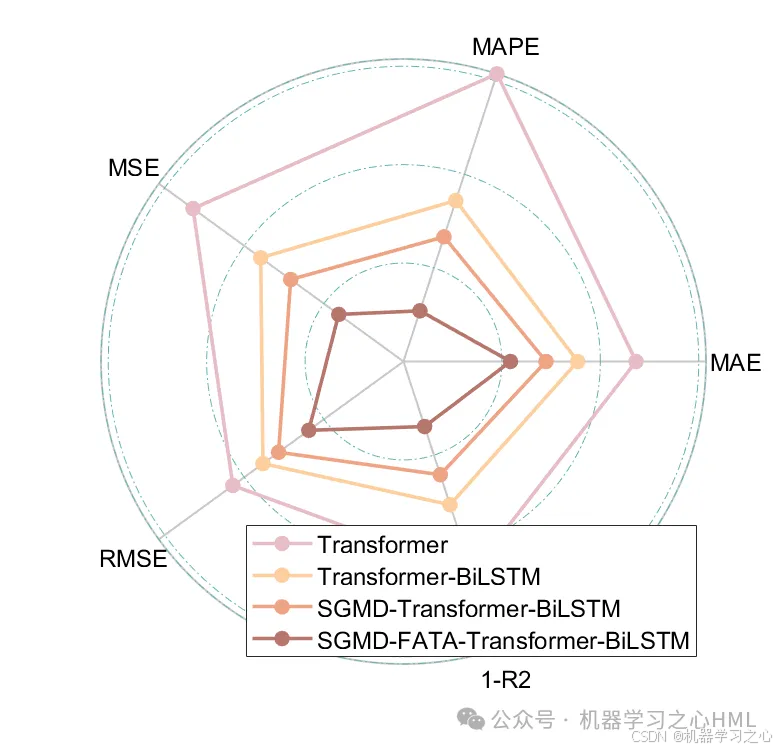
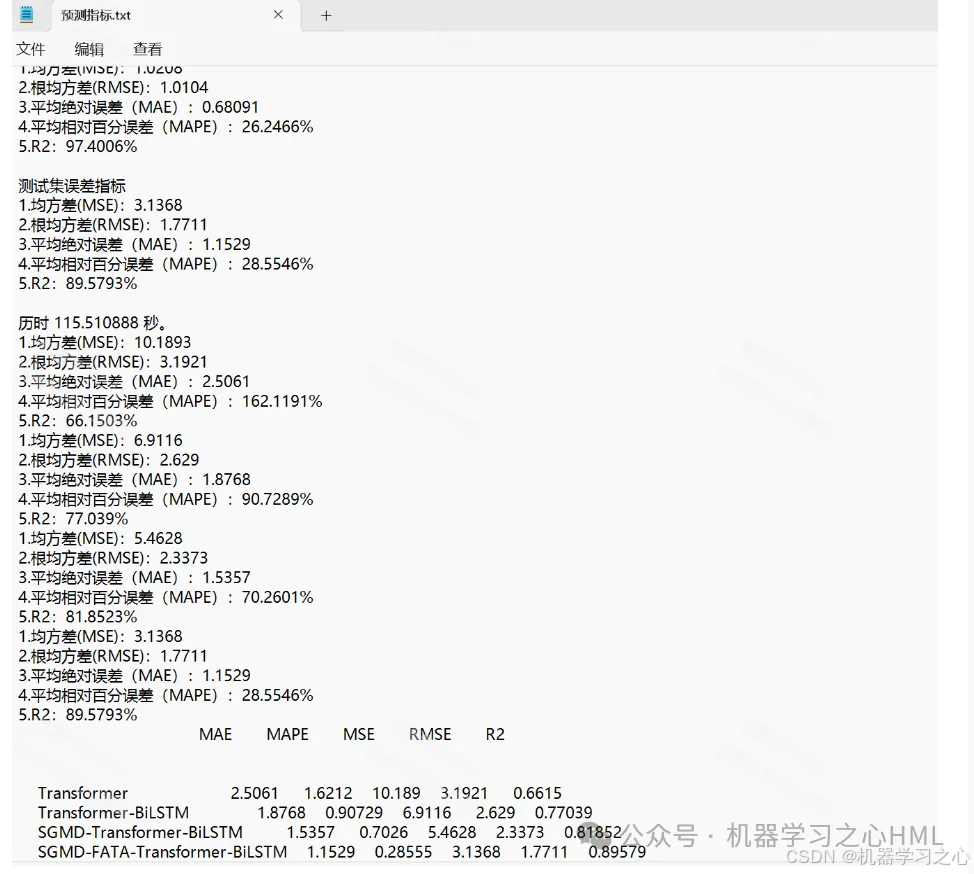
4.命令窗口输出R2、MSE、RMSE、MAE、MAPE、MBE等多指标评价。
先运行main1SGMD，进行SGMD分解；再运行main2FATATransformerBiLSTM，四个模型对比；注意：一种算法不是万能的，不同的数据集效果会有差别，后面的工作就是需要调整参数。

数据集
在这里插入图片描述

参考文献
在这里插入图片描述

程序设计

完整程序和数据获取方式私信博主回复闹海闹元宵！顶刊算法+分解组合+四模型对比！SGMD-FATA-Transformer-BiLSTM多变量时间序列预测（Matlab）。



%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

clc;
clear 
close all
warning off
%% CSDN《机器学习之心》
%% Transformer预测
tic
X = xlsread('北半球光伏数据.xlsx');
load SGMD_data.mat


disp('…………………………………………………………………………………………………………………………')

num_samples = length(X);       % 样本个数 
kim = 5;                       % 延时步长（kim个历史数据作为自变量）
zim =  1;                      % 跨zim个时间点进行预测
or_dim = size(X,2);

%  重构数据集
for i = 1: num_samples - kim - zim + 1
    res(i, :) = [reshape(X(i: i + kim - 1,:), 1, kim*or_dim), X(i + kim + zim - 1,:)];
end


% 训练集和测试集划分
outdim = 1;                                  % 最后一列为输出
num_size = 0.7;                              % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度


P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);

%  数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  数据平铺
%   将数据平铺成1维数据只是一种处理方式
%   也可以平铺成2维数据，以及3维数据，需要修改对应模型结构
%   但是应该始终和输入层数据结构保持一致
P_train =  double(reshape(P_train, f_, 1, 1, M));
P_test  =  double(reshape(P_test , f_, 1, 1, N));

t_train = t_train';
t_test  = t_test' ;

%%  数据格式转换%% CSDN《机 器 学 习 之 心》
for i = 1 : M
    p_train{i, 1} = P_train(:, :, 1, i);
end

for i = 1 : N
    p_test{i, 1}  = P_test( :, :, 1, i);
end

% Transformer建模
numChannels = f_;                                             % 定义输入的通道数，变量 f_ 代表特征的维度
maxPosition = 256*2;                                          % 最大位置编码，通常用于序列长度的上限，这里设为 512
numHeads = 4;                                                 % 自注意力机制中的头数
numKeyChannels = numHeads*32;                                 % 每个头的键通道数，总键通道数为 128

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/127931217
[2] https://blog.csdn.net/kjm13182345320/article/details/127418340