关于P2P-文件共享软件的一些思考

笔者最近想开发一套P2P文件共享软件，对于UDP/TCP协议的NAT穿透在过年期间也算是打通了。目前就我对P2P文件共享软件开发的一些探索这里记录一点心得。

关于Kademlia 分布式DHT算法，我在网上查阅了不少文章，我觉得这篇文章对我有着重大影响

尽管我不知道自己对Kademlia算法是否完全理解或者理解正确。

一、达成共识

我们每台计算机，这里称之为节点（Node），在与之不同局域网也就是NAT背后的节点通信时，是会被NAT设备拒绝的，那么这里要想能够直接进行点对点的通讯，必须穿透NAT，也就是我们俗称的NAT打洞，在成功打洞后方可以建立每个节点的直接连接（对等连接）。在这个过程中，我们需要借助公网服务器的协调来完成打洞行为。（好，那么所谓的完全去中心化，没有公网服务器的条件下，完成NAT穿透，笔者认为目前在基于IPv4的条件下，是不太可能的。）所以，这篇文章笔者会引入两台公网服务器用于辅助客户端进行打洞并完成节点之间的对等连接。

二、初探Kademlia算法

各位看官，若有对Kademlia算法感兴趣的朋友可以借鉴我引入的链接博客。

在基于笔者对Kademlia算法的学习后，有一定的思考，笔者先提供一下代码，各位看官可以在自己的电脑中运行代码并跟着笔者的思路往下走。

#include <iostream>
#include <vector>
#include <algorithm>

class KBucketsTest
{
public:

// 假设节点 ID 是 160 位的整数
typedef unsigned long long NodeID;

std::vector<std::vector<NodeID>> currentClientKBuckets;  // 全局变量存储当前客户端的 k 桶

// 计算两个节点 ID 的异或距离
unsigned int calculateDistance(NodeID node1, NodeID node2) {
    return static_cast<unsigned int>(node1 ^ node2);
}

// 插入节点到对应的 k 桶
void insertNodeIntoKBucket(NodeID newNode, int k) {
    int bucketIndex = 0;
    while (bucketIndex < 160) {  // 假设最多有 160 个 k 桶，根据实际情况调整
        // 计算新节点到当前桶的距离范围
        unsigned int minDistance = 1 << bucketIndex;
        unsigned int maxDistance = (1 << (bucketIndex + 1)) - 1;

        // 如果新节点在当前桶的距离范围内
        if (calculateDistance(newNode, minDistance) <= maxDistance) {
            // 获取当前桶
            auto& bucket = currentClientKBuckets[bucketIndex];

            // 如果桶未满，直接插入到桶的末尾
            if (bucket.size() < k) {
                bucket.push_back(newNode);
                return;
            }

            // 桶已满，ping 桶头部节点检查是否存活
            NodeID headNode = bucket.front();
            // 这里模拟 ping 操作，假设返回 true 表示节点存活
            bool isHeadNodeAlive = true;

            if (isHeadNodeAlive) {
                // 头部节点存活，将其移到桶的末尾，忽略新节点
                std::rotate(bucket.begin(), bucket.begin() + 1, bucket.end());
            }
            else {
                // 头部节点不存活，移除头部节点，插入新节点到末尾
                bucket.erase(bucket.begin());
                bucket.push_back(newNode);
            }

            return;
        }

        bucketIndex++;
    }
}

int main() {
    // 初始化 k 桶
    currentClientKBuckets.resize(160);
    int k = 16;  // 每个 k 桶中存储的节点数量

   
    for(int i = 1;i < 1000; ++ i)
    {
        NodeID newNodeId = i;
        insertNodeIntoKBucket(newNodeId, k);
    }
  
   


    // 打印 k 桶的内容（仅用于示例）
    for (const auto& bucket : currentClientKBuckets) {
        std::cout << "[";
        for (const auto& node : bucket) {
            std::cout << node << ",";
        }
        std::cout << "]" << std::endl;
        std::cout << std::endl;
    }

    return 0;
}

};

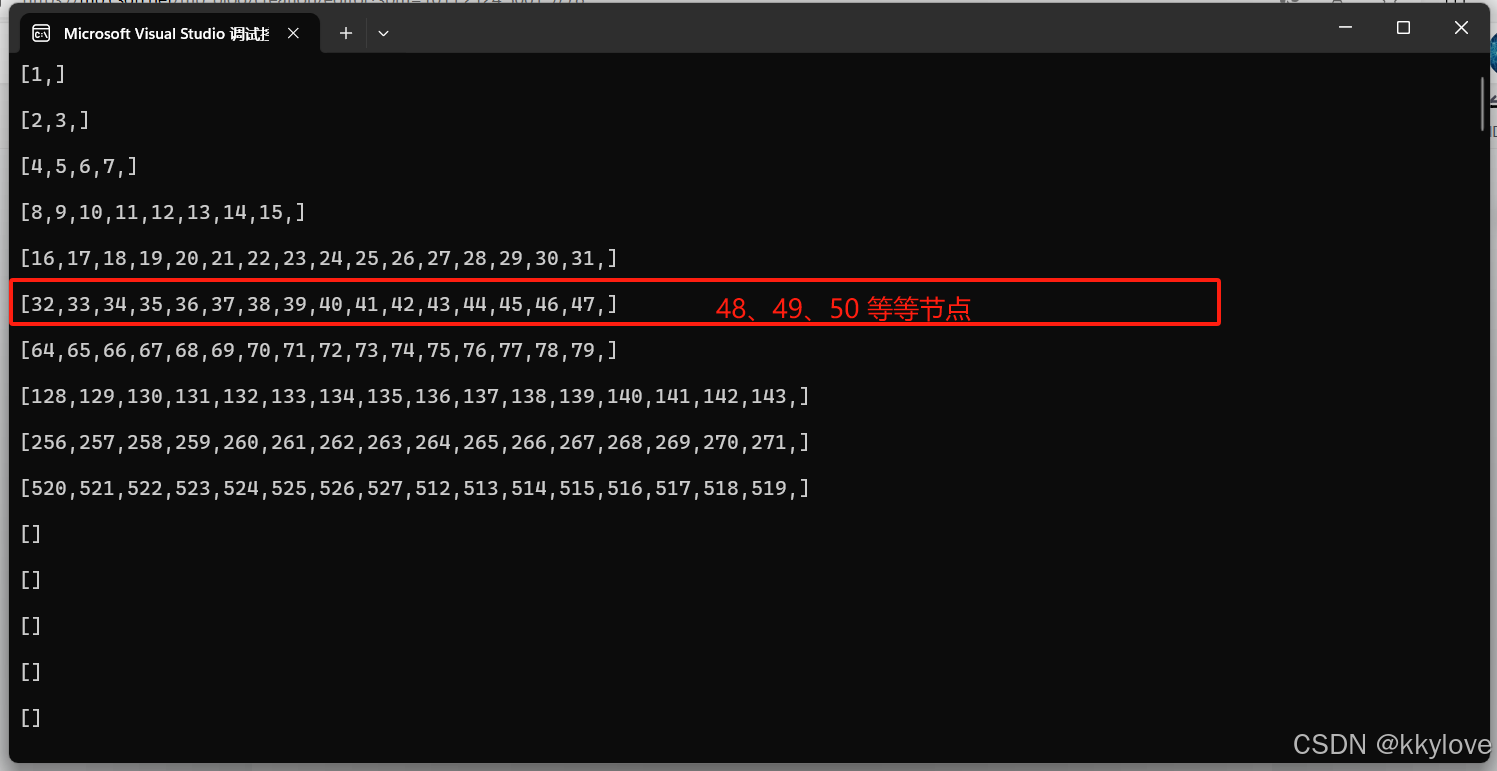
运行上述代码可以获得的数据结果为：

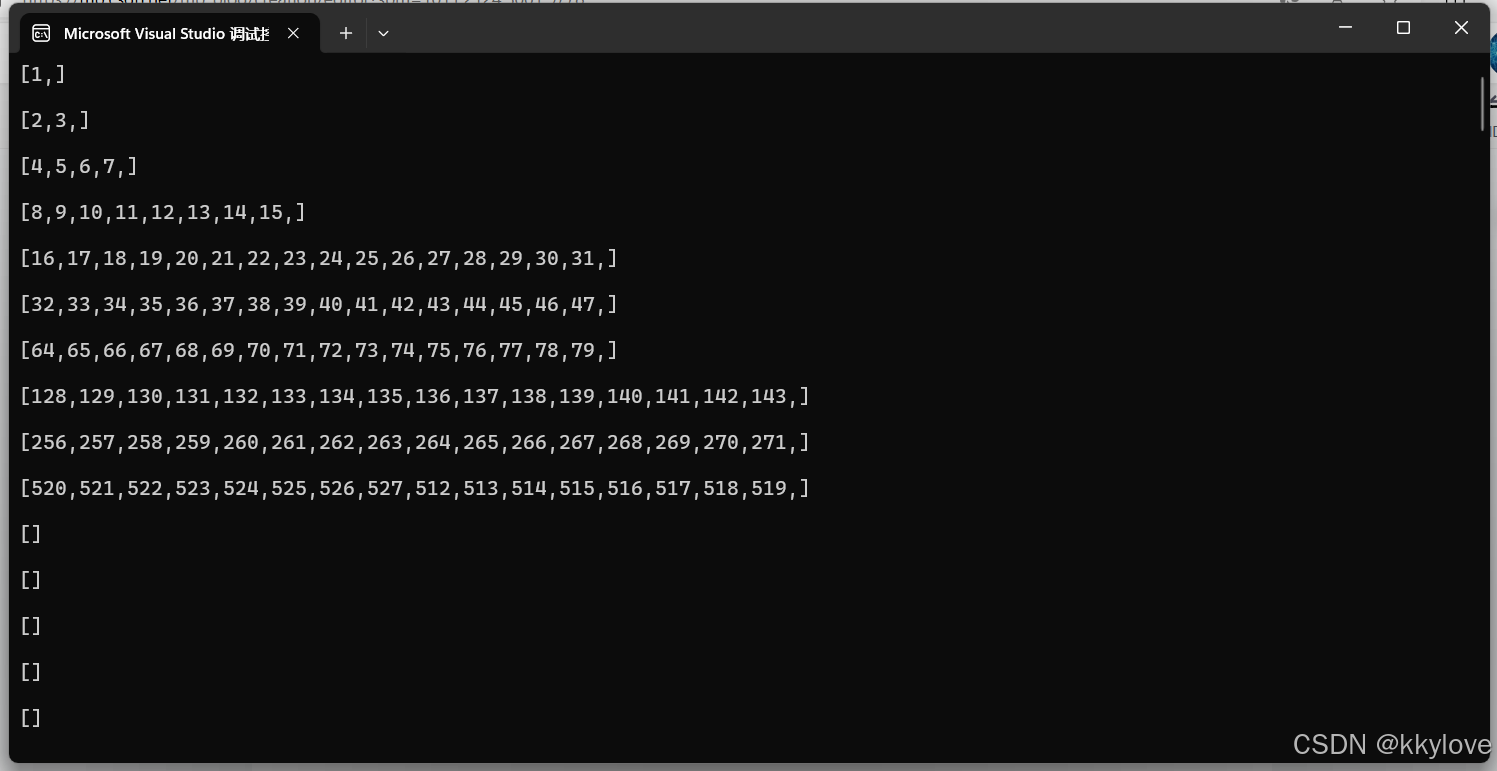
看到如上图所示的k桶输出后（每个[1、]、[2、3、]......括号中的数字表示的是一个在线节点）

笔者在代码中将k这个变量设置成了16，k=16；也就是说k桶的最大容量是16，最大容纳16个节点信息。按照笔者对k桶的设想，k桶中的每个节点必须是活跃的，也就是说一旦有节点离线，将会自动将后补节点加入到当前k桶列表的尾端中用来补充并维持k桶的节点在容量的最大范围以内。

根据笔者分享的链接中提供的算法：（[2(n-1)、2(n)) ，2的n-1次方，2的n次方）我们可以推导出来，每个节点应该归于哪个k桶之内。结合笔者提供的下图来看

在第6行，笔者框红的列表中只有16个节点，实际上48、49、50直到63这个序列的节点也应该归于这个k桶。只是笔者在上述代码中限制了k桶的容量，所以后续的节点被排除了，当然，这些被排除的节点在距离上也满足（[2(n-1)、2(n)) ，2的n-1次方，2的n次方）的区间限制范围。这里说一点，假设：节点32离线了，那么作为后补节点的48可能就要补充到这个k桶中来。

基于以上的这些分析：

笔者有个设想，如果一个节点【32】共享了一份文件叫做【分布式DHT算法的书】，那么我可否将这本书的hash计算出来，同时让当前节点的k桶中的其他所有节点【33、34、35、36...47】同时维护这本书的hash，尽管实际上这本书的实物只存储在【32】这个节点中。那么，以此类推，只要有一个节点共享了他的文件，他的k桶中的其他节点都具有这份文件的hash。

那么，如果当【1】这个节点需要下载【分布式DHT算法的书】时，首先对公网服务器发起查询，假设公网服务器一共只维护了10个k桶，如上图所示。那么公网服务器只需要在k桶列表中分别取出一个节点进行询问，你是否有【分布式DHT算法的书】，含有这本书的节点就可以相应我们的公网服务器【好happy，我正好有这本书的hash】，为什么说是hash，那是因为书的实物并不一定在自己手上，而是这本书的hash。那么，经过一层筛选后，我们是否可以继续询问这本书的实物在谁手上，然后通过多次查询后，将具有书实物的节点就筛选出来了。

接下来：

接下来咱们是否就要分割文件，假设实物在【2、3】这个k桶的2号节点手上有，同时，在【520、521...】k桶的520节点手上有，那么咱们就可以将文件分割成若干等分，让1号节点去借助公网服务器打洞穿透2号节点与520节点的内网，从而进行对等连接后愉快的下载【分布式DHT算法的书】这本书啦。

关于P2P-文件共享软件的一些思考

悦读