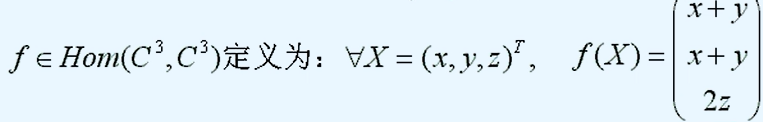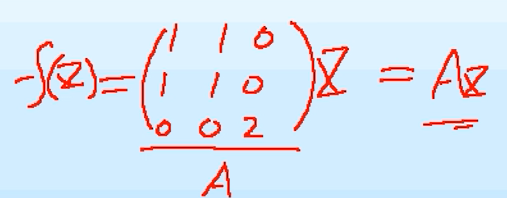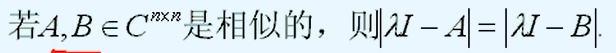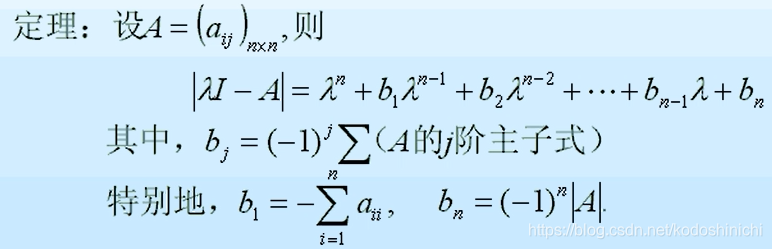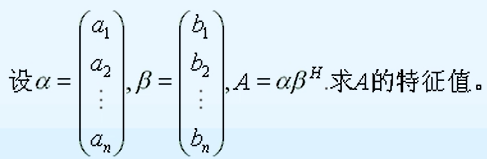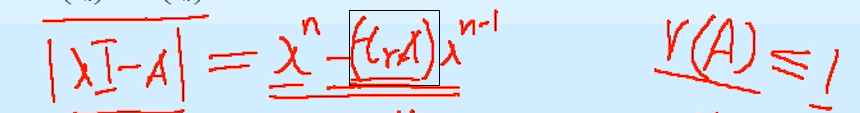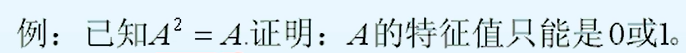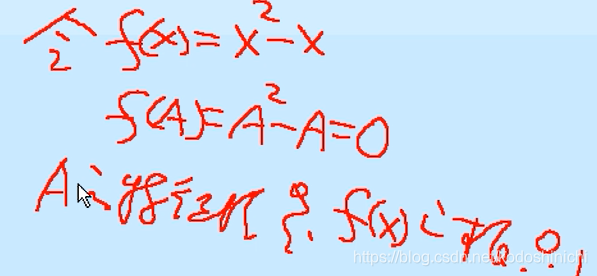矩阵的相似标准型之“特征值与特征向量”

本章目的：

• 对于给定的矩阵，找一个最简单的矩阵与之相似
• 对于给定的线性空间上的线性变换，找线性空间的一组基，使得线性变换的矩阵最简单。
  
  p.s. 在《【矩阵论】线性空间与线性变换（5）》这篇博文中我们对线性映射（变换）进行了十分详细的讨论，其中就提到一条定理如下图所示：
  
  所以，当用线性变换的角度来看待矩阵时，找一个最简单的相似矩阵实质上就是找到一组基，使得该基下的矩阵表示尽可能的简单。

一. 线性代数回顾

1. 矩阵的相似对角化问题

矩阵的相似对角化是说，对于一个矩阵A，如果存在一个可逆矩阵P，用这个可逆矩阵对A进行初等变换——P^-1AP之后，即可以把矩阵A化成一个对角阵的形式，那么就说矩阵A可以进行相似对角化。

如果把矩阵P进行列分块表示成[p1,p2,p3,…,pn]的形式，那么对上式进行一个等价变换为AP = PΛ的形式，根据分块矩阵和对角矩阵运算的特点，就能得到APj = λj·Pj的形式。

也就是说，A矩阵相似对角化之后得到的矩阵对角线上的每一个元素都是A的特征值，而变换矩阵P的每一列就是相对应的特征向量。

p.s. 这里再推荐一篇“线性代数本质”系列的博文，是我看3Blue1Brown的同名系列视频所做的随课笔记，有一节《【线性代数的本质|笔记】基变换、特征向量和特征值》就是从几何上的观点来讲解矩阵的特征值和特征向量，对于建立线性代数中概念的直观印象很有帮助。

2. 矩阵特征值、特征向量的计算

（1）特征值、特征向量的定义

对于一个矩阵A，若存在一个数λ0和一个非零向量η，使得Aη = λ0η成立，那么就称λ0是矩阵A的一个特征值，而η就是矩阵A关于特征值λ0的一个特征向量。

（2）特征值、特征向量的计算

根据Aη = λ0η这个等式，可以将矩阵方程转化成（λ0I-A）η = θ的形式，因此我们要求解的特征向量就是齐次方程组（λ0I-A）η = θ的非零解。

一个齐次线性方程组具有非零解的充要条件就是这个系数矩阵的行列式（也就是|λ0I-A|，被称作是特征多项式）应该为零（系数矩阵不是一个满秩矩阵）。
令|λ0I-A| = 0,求解这个特征方程，得到相应的特征值，将特征值回代入齐次方程中就能得到相应的特征向量。

以下的这一节的主体内容，我们就是要用线性变换的语言和角度来思考“特征值和特征向量”这些概念

二. 线性变换的特征值和特征向量

1. 定义

线性变换角度的特征量定义与线性代数中的十分类似，读者可以进行类比理解，毕竟我们本身就可以用线性变换的角度来看待矩阵。

讨论线性变换的特征量的意义也就在于对线性变换的矩阵表示进行简化

对于一个线性变换f∈Hom(V,V),λ0∈F，η∈V（且η≠0），若f(η) = λ0η，则称——
λ0是线性变换f的特征值
η是线性变换f的特征向量

2. 数学求解

（1）【例1】对于给定的线性变换，求解其特征值和特征向量

【方法论】

当线性变换f可以写成对于空间中任意一个向量x进行形如f(x)= Ax的变换形式时，线性变换f的特征值与特征向量实质上就是矩阵A的特征值和特征向量

求解：根据题意，上述线性变换f可以很容易地转换成矩阵的表示形式，所以问题就转换成求矩阵A的特征值与特征向量了，此处详细计算过程不再列写。

（2）【例2】一般的线性变换的特征量求解

【结论推广】

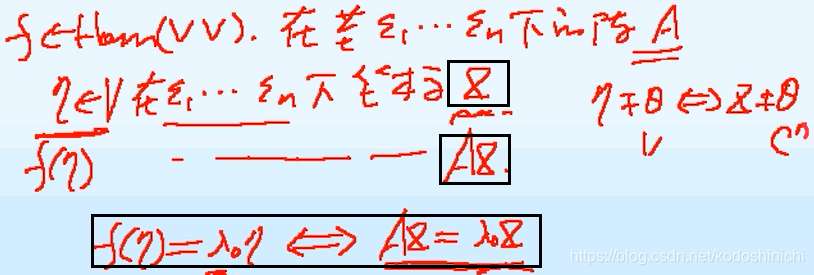
在上一个例子中给出的变换矩阵是很具体的，但其实“线性变换的特征量↔线性变换对应的矩阵的特征量”这个结论是可以在一般线性变换中进行拓展的。


根据上图，在指定的一组基下，原像的坐标为X，那么根据线性变换的矩阵表示，变换后的像的坐标可以写成AX，如果一个向量η是线性变换A的特征向量，那么就有f(η) = λη的等式成立，此处像与原像之间的关系就可以直接转换成像的坐标与原像的坐标之间的关系——AX = λX，从而得证。

p.s. 要注意像（和原像）所在的线性空间与像的坐标（原像的坐标）所在的线性空间并不一致。

（3）【例3】任意一个线性空间中给定的线性变换的特征量的求解

【方法论】
①首先找到该线性空间的一组基，把这个空间内定义的线性变换用矩阵的形式表示出来。
p.s. 这里要注意一下，给定的线性空间可能是各式各样的，但是找到基之后给出的矩阵，其一定是在最一般的矩阵空间R^mxn之中（m,n的数值取决于变换前后的向量维度）

②对第一步找到的矩阵A进行特征量的求解

③特征值的求解一般不会出问题，但是我们找出来的矩阵A的特征向量往往是在Rⁿ空间中的，还需要根据题意中定义的X所处的空间形式，将特征向量变换成其原来的形式。

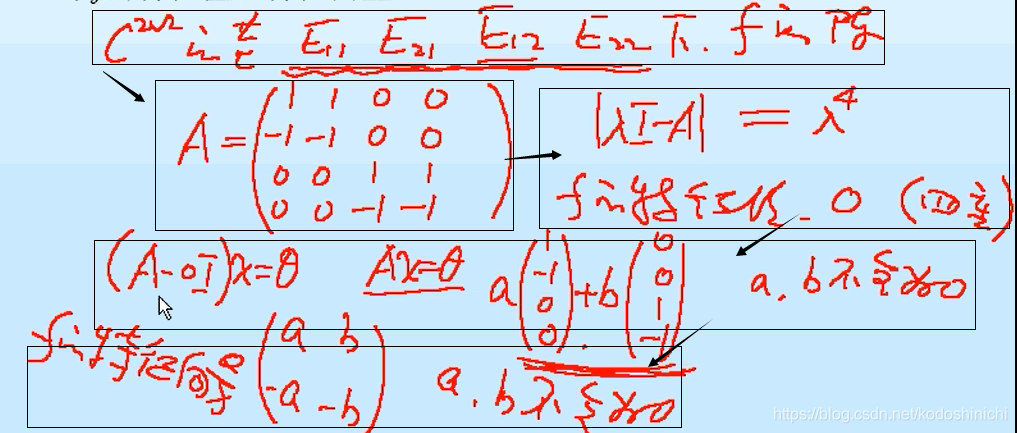
Tip1：为了简化计算（后面得到的矩阵A是分块对角的形式，进行行列式等运算时会更加方便），老师选择的一组基并不是我们通常取的顺序E11，E12，E21，E22，；而是进行了小小的调整。

Tip2：因为取的基的顺序发生了变化，所以在写向量坐标，以及求方程解还有将特征向量还原成原来空间形式的时候都要注意顺序，不要惯性思维。

Tip3：如果只是对矩阵A进行求解，那么a[1,-1,0,0]^T+b[0,0,1,-1]^T的形式就已经是矩阵A的特征向量形式了，但是原来的向量X是在C^2x2空间中，所以我们还要根据选取的基E11，E21，E12，E22将特征向量还原成[[a,b],[-a,-b]]的形式。

Tip4：这一部分，涉及到很多线性空间的转换，如果理解的不是很好，我建议还是戳下方的原视频听听老师讲解，老师讲的思路很清晰。

3. 相关定理

（1）相似矩阵具有相同的特征量

简要证明：

注：
①上述定理的逆命题并不成立；e.g. A = [[0,0],[0,0]],B = [[0,1],[0,0]]

②可以由此定理定义线性变换的特征多项式
“在之前，如果线性变换在某一组基下的矩阵为A，那么我们就可以用A的特征多项式来代表线性变换的特征多项式；但是我们也知道一个线性变换在不同的基下会有不同的矩阵表示，难免会产生困扰——那么一个线性变换是否会有不同的特征多项式与之对应？经过这个定理，我们就知道只要是同一个线性变换，其不同的矩阵对应的特征多项式都是一样的，这就定义了线性变换的特征多项式的唯一性。”

（2）特征多项式的计算

一个矩阵A的特征多项式是形如|λI-A|这样的多项式，其中λ为多项式中的未知参数，I是单位矩阵，||是取行列式运算。

我们知道如果将行列式展开应该能得到一个关于λ的n次多项式（n为矩阵A的阶数），而各个阶的项前的系数也应该和矩阵A的某些项相关，我们希望能够找到系数的规律，从而可以简化特征多项式的求解。

通俗地来说，矩阵的k阶主子式，就是沿着主对角线方向连续取的一个k阶子矩阵的行列式。

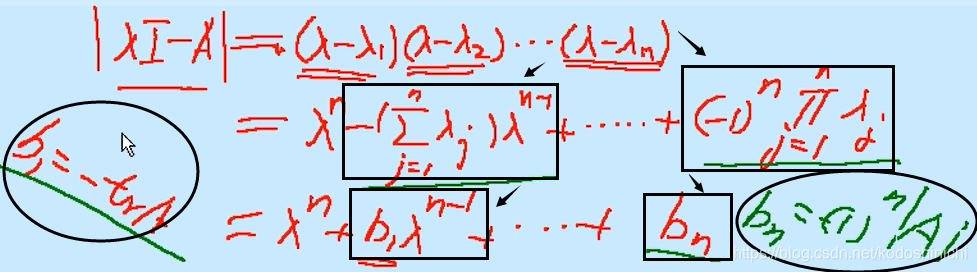
（3）矩阵的迹

在上面的定理中，与求子式相比，求解对角线元素的和，求解原矩阵的行列式会更加简单，所以这里要把这两个特别的项b1和b2得到结论记住。

“矩阵A的迹（对角线上元素之和）等于矩阵A的特征值之和”

“矩阵A的行列式等于特征值元素的乘积”

因为已知了矩阵A的各个特征值，所以可以把特征多项式|λI-A|写成(λ-λ1)·(λ-λ2)·…·(λ-λn)的形式，再对照左右等式两边项的系数，就能证明上述结论。

关于推论，前面已经讨论过【两个相似的矩阵具有相同的特征多项式】，结合此处的结论，可以得到【两个相似的矩阵具有相同的特征量（特征多项式，迹，矩阵行列式等等）】

（4）例题求解

【例】利用相关定理求解矩阵的特征量

OS:看完这一段老师的讲解视频之后，内心的想法就是老师真的有很多很多奇妙但是又好用的小结论，可以很大程度上减少计算量。而老师能够达到这样的境界，我觉得跟熟悉程度以及对线代、线性空间等概念的建立了直观印象是分不开的。

以下会对证明过程完整列述（老师的证明真的十分通透清楚！！），如果想看视频的也可以直接点进原视频48份27秒处。
《第三章 矩阵的相似标准型（1）》

要求解A的特征值，最通用的想法就是求解矩阵A的特征方程，然后得到各个特征值的解。
因为α和β都是列向量，所以可以分析出来矩阵A是一个n阶方阵，由此得到A的特征多项式的一般形式。

【奇奇妙妙小结论1】
行向量乘以列向量形式的矩阵的秩不会大于1；

这是由矩阵的秩的相关性质得到的，两个矩阵A和B的乘积的秩不会大于每一个因子矩阵的秩。

因此可得到A的特征多项式中，k阶子式（k>1）都为0，所以特征多项式中只含有n阶项和n-1阶项。
前面已经得到了结论，n-1阶项的系数就是矩阵A的迹，问题就转化成求矩阵A的迹。

【奇奇妙妙小结论2】
tr(A·B) = tr(B·A)

虽然矩阵的乘法是不具有交换性的，且只要AB和BA运算能够成立（不需要二者结果相同）就有上述结论成立

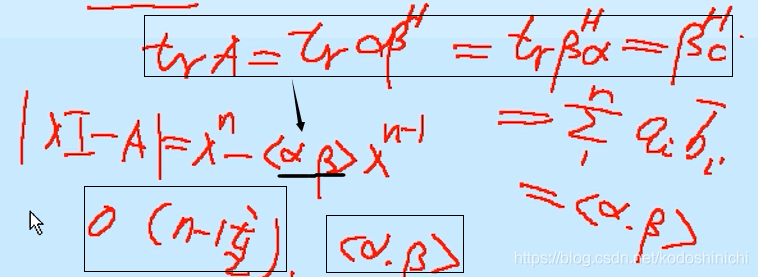
因为矩阵A的迹就转换成求β^H·α的迹，而β^H·α的结果就是1阶矩阵，它的迹也就是它本身。

如上图求解出来一个n-1重根0还有一个根<α，β>
但是这里的讨论并不完全，如果向量α和β本身就是正交的话，那么求解出来的特征值只有0（n重根）。

三. 化零多项式

根据前文，我们讨论了特征量（特征值、特征向量、特征多项式、特征方程等）的定义以及性质定理，并且也通过例题求解感受到了，如果要求解一个矩阵的特征值，最基本的方法就是把矩阵的特征多项式写出来，然后进行方程求解。

但是同时我们也在思考，是不是存在一个方法，我们不需要计算特征多项式，可以只通过线性变换（或其他）等手段，就可以求解出一个矩阵的特征值呢？

基于此，我们提出了化零多项式的概念

1. 定义

设f(x)是一个多项式，对于一个矩阵A，如果有f(A) = O,那么就称f(x)是矩阵A的化零多项式。

性质：如果一个矩阵A的化零多项式为f(x),那么A的特征值就是化零多项式构成的方程f(x) = 0的根。

证明：
按照特征值和特征向量的定义，对于矩阵A，存在一个数λ还有一个非零向量η，如果有Aη = λη成立，那么就说λ是矩阵A的一个特征值，而η是矩阵A关于特征值λ的一个特征向量。

并且上述关系还可以延伸定义成A^kη = λ^kη的形式，也就是说对于任意一个多项式φ(x)，一定有φ(A)η = φ(λ)η成立。

用f(A)来整体替换φ(A)，故可以得到f(A)η = f(λ)η；又因为f(A) = O，所以等式左边得到一个零向量θ，且已知η≠θ的前提下，只有f(λ) = 0.
证毕

注意：
①利用上述定义和定理，当我们不知道矩阵A的特征多项式的情况下，可以通过求解矩阵A的化零多项式来得到矩阵A可能的特征值。

②A的特征值都是f(x) = 0的根，但是f(x) = 0的根并不一定都是矩阵A的特征值。

2. 例题练习

【例】根据化零多项式进行特征量的有关求解。

【幂等矩阵】
满足Aⁿ = A 形式的矩阵称为幂等矩阵

通过题意给出的幂等矩阵的形式，可以很容易地构造出一个化零多项式。

同样地，要注意这里的文字表述。矩阵A的特征值只可能是0或是1，并不意味着这0和1都是矩阵A的特征值。

e.g. 比如说单位阵I和零矩阵O都是满足上述条件的幂等矩阵，其特征值分别只有0和1.

而且通过化零多项式求解出来的候选特征值，也是无法确定其重数的。