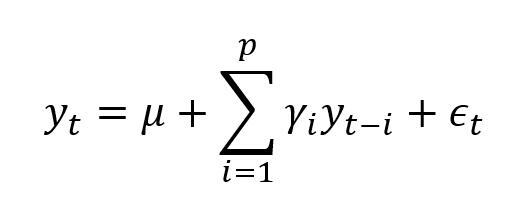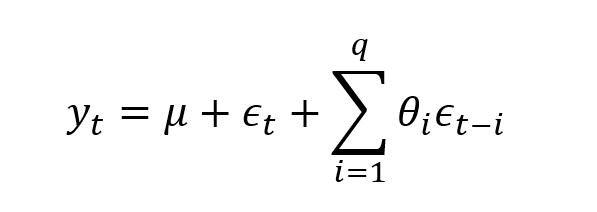Autoregressive Integrated Moving Average Model,即自回归移动平均模型。它属于统计模型中最常见的一种,用于进行时间序列的预测。其原理在于:在将非平稳时间序列转化为平稳时间序列的过程中,将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。
其实就是三大块的整合
1.自回归model
自回归模型是描述当前值与历史值之间的关系的模型,是一种用变量自身的历史事件数据对自身进行预测的方法。其公式如下:
其中,yt是当前值;μ是常数项;p是阶数;γi是自相关系数,ϵt是误差值。
自回归模型的使用有以下四项限制:
该模型用自身的数据进行预测,即建模使用的数据与预测使用的数据是同一组数据;使用的数据必须具有平稳性;使用的数据必须有自相关性,如果自相关系数小于0.5,则不宜采用自回归模型;自回国模型只适用于预测与自身前期相关的现象。
2.integrated
ARIMA模型最重要的地方在于时序数据的平稳性。平稳性是要求经由样本时间序列得到的拟合曲线在未来的短时间内能够顺着现有的形态惯性地延续下去,即数据的均值、方差理论上不应有过大的变化。平稳性可以分为严平稳与弱平稳两类。严平稳指的是数据的分布不随着时间的改变而改变;而弱平稳指的是数据的期望与向关系数(即依赖性)不发生改变。在实际应用的过程中,严平稳过于理想化与理论化,绝大多数的情况应该属于弱平稳。对于不平稳的数据,我们应当对数据进行平文化处理。最常用的手段便是差分法,计算时间序列中t时刻与t-1时刻的差值,从而得到一个新的、更平稳的时间序列。
3.moving average
移动平均模型关注的是自回归模型中的误差项的累加。它能够有效地消除预测中的随机波动。
1+3=ARMA
在这个公式中,p与q分别为自回归模型与移动平均模型的阶数,是需要人为定义的。γi与θi分别是两个模型的相关系数,是需要求解的。如果原始数据不满足平稳性要求而进行了差分,则为差分自相关移动平均模型(ARIMA),将差分后所得的新数据带入ARMA公式中即可
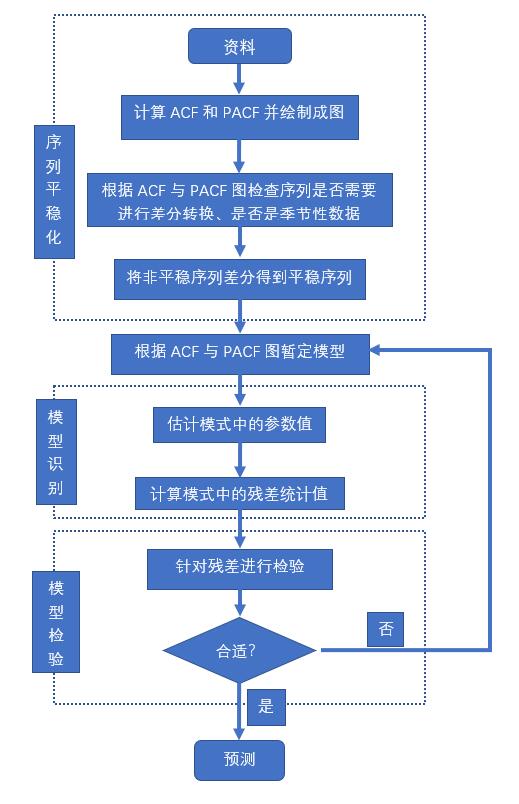
流程:
自相关函数(ACF)是将有序的随机变量序列与其自身相比较,它反映了同一序列在不同时序的取值之间的相关性。
偏自相关函数(PACF)计算的是严格的两个变量之间的相关性,是剔除了中间变量的干扰之后所得到的两个变量之间的相关程度。对于一个平稳的AR(p)模型,求出滞后为k的自相关系数p(k)时,实际所得并不是x(t)与x(t-k)之间的相关关系。这是因为在这两个变量之间还存在k-1个变量,它们会对这个自相关系数产生一系列的影响,而这个k-1个变量本身又是与x(t-k)相关的。这对自相关系数p(k)的计算是一个不小的干扰。而偏自相关函数可以剔除这些干扰
- p: The number of lag observations included in the model, also called the lag order.
- d: The number of times that the raw observations are differenced, also called the degree of differencing.
- q: The size of the moving average window, also called the order of moving average.
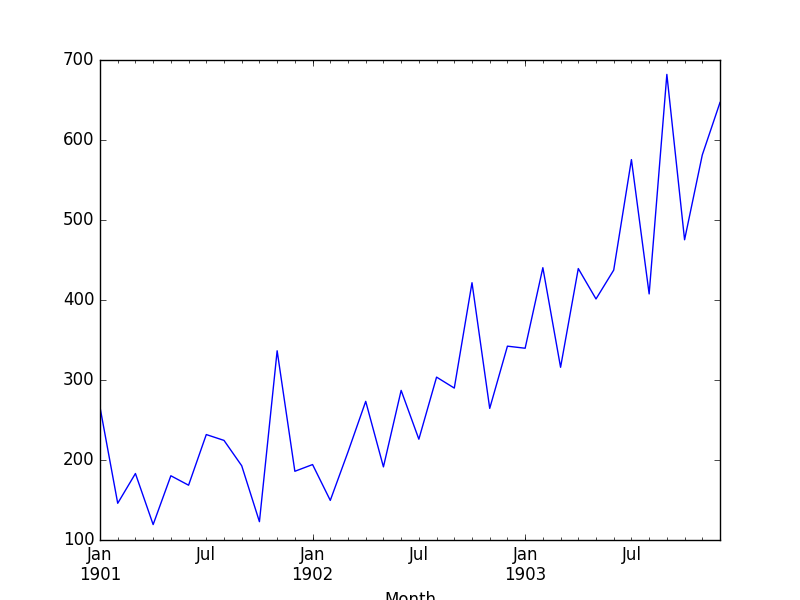
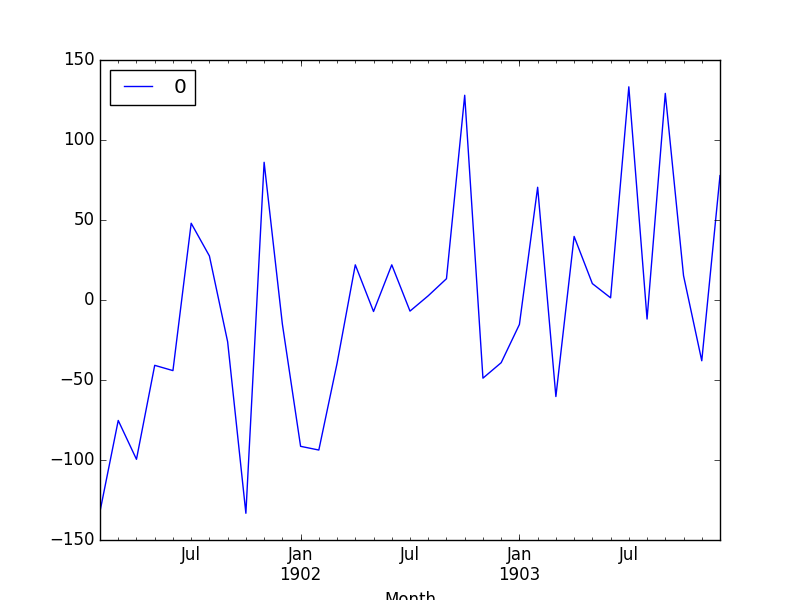
我们的序列张这样,可以看出来存在趋势,不平稳所以需要差分(至少一次差分,你可以用adf检验获取更具有统计意义的结果,参考:https://www.jianshu.com/p/4130bac8ebec)
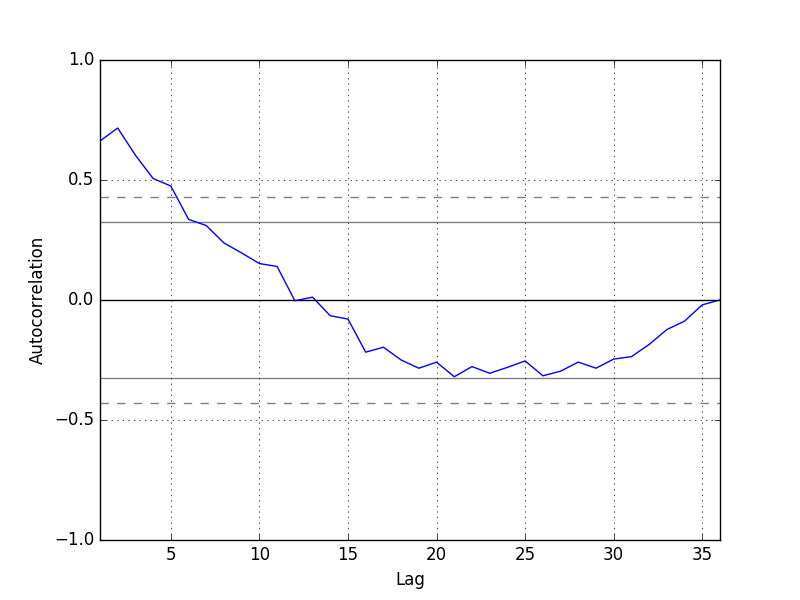
自回归图长这样,所以我们大致选择滞后项为5(更精确的选择可以参考上面链接)
from pandas import read_csv
from pandas import datetime
from pandas import DataFrame
from statsmodels.tsa.arima_model import ARIMA
from matplotlib import pyplot
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# fit model
model = ARIMA(series, order=(5,1,0))
model_fit = model.fit(disp=0)
print(model_fit.summary())
# plot residual errors
residuals = DataFrame(model_fit.resid)
residuals.plot()
pyplot.show()
residuals.plot(kind='kde')
pyplot.show()
print(residuals.describe())这里我们选择lag=5,差分=1,MA=0看看模型
ARIMA Model Results
==============================================================================
Dep. Variable: D.Sales No. Observations: 35
Model: ARIMA(5, 1, 0) Log Likelihood -196.170
Method: css-mle S.D. of innovations 64.241
Date: Mon, 12 Dec 2016 AIC 406.340
Time: 11:09:13 BIC 417.227
Sample: 02-01-1901 HQIC 410.098
- 12-01-1903
=================================================================================
coef std err z P>|z| [95.0% Conf. Int.]
---------------------------------------------------------------------------------
const 12.0649 3.652 3.304 0.003 4.908 19.222
ar.L1.D.Sales -1.1082 0.183 -6.063 0.000 -1.466 -0.750
ar.L2.D.Sales -0.6203 0.282 -2.203 0.036 -1.172 -0.068
ar.L3.D.Sales -0.3606 0.295 -1.222 0.231 -0.939 0.218
ar.L4.D.Sales -0.1252 0.280 -0.447 0.658 -0.674 0.424
ar.L5.D.Sales 0.1289 0.191 0.673 0.506 -0.246 0.504
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.0617 -0.5064j 1.1763 -0.4292
AR.2 -1.0617 +0.5064j 1.1763 0.4292
AR.3 0.0816 -1.3804j 1.3828 -0.2406
AR.4 0.0816 +1.3804j 1.3828 0.2406
AR.5 2.9315 -0.0000j 2.9315 -0.0000
-----------------------------------------------------------------------------
最后那个roots其实没太明白是什么玩意。。。。
上面是残差图,可以看出来并不会杂乱无章,所以说明我们的模型不是很好
count 35.000000
mean -5.495213
std 68.132882
min -133.296597
25% -42.477935
50% -7.186584
75% 24.748357
max 133.237980
残差均值也不=0,所以确实模型不好啊
按理说残差表现好才能预测,那先假设残差表现好把
如果我们使用训练数据集中的100个观测值来拟合模型,那么预测的下一个时间步的索引将被指定给预测函数start=101, end=101。这将返回一个包含预测的元素的数组。
如果在配置模型时执行了任何不同操作(d>0),我们也希望预测的值保持在原始的比例。这可以通过将typ参数设置为值“levels”来指定:typ=“levels”。
另外,我们可以通过使用forecast()函数来避免所有这些规范,该函数使用模型执行一步预测。我们可以将训练数据集分为训练集和测试集,使用训练集来拟合模型,并为测试集上的每个元素生成一个预测。
考虑到对差分和AR模型的依赖,需要滚动预测。执行滚动预测的一种粗略方法是在每次接收到新的观测之后重新创建ARIMA模型。
我们手动跟踪一个名为history的列表中的所有观察结果,这个列表中包含了培训数据,并且每个迭代都会添加新的观察结果。把这些放在一起,下面是一个使用Python中的ARIMA模型滚动预测的示例。
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
X = series.values
size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]
history = [x for x in train]
predictions = list()
for t in range(len(test)):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test[t]
history.append(obs) # 这里实现了滚动预测,应该是ARIMA只能预测下一步而不能多步
print('predicted=%f, expected=%f' % (yhat, obs))
error = mean_squared_error(test, predictions)
print('Test MSE: %.3f' % error)
# plot
pyplot.plot(test)
pyplot.plot(predictions, color='red')
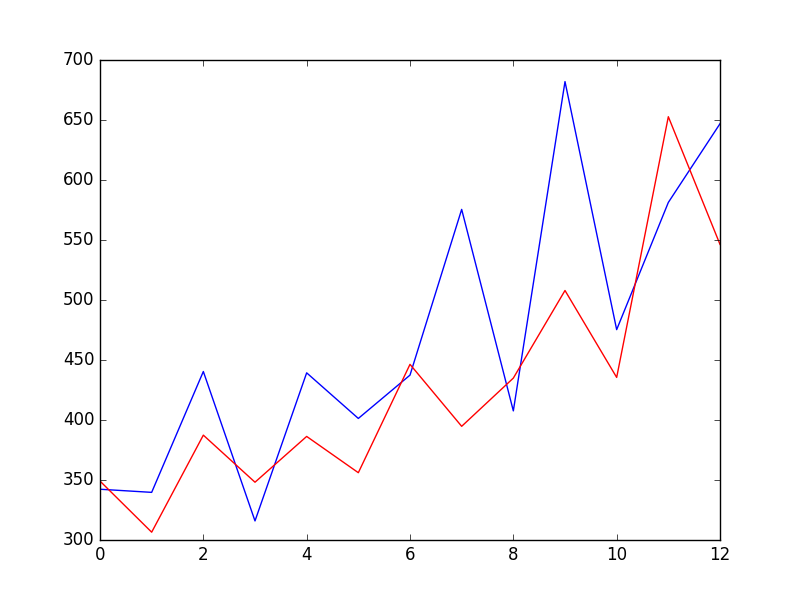
pyplot.show()效果图如上
https://machinelearningmastery.com/arima-for-time-series-forecasting-with-python/
使用建议:
https://machinelearningmastery.com/gentle-introduction-box-jenkins-method-time-series-forecasting/
https://blog.csdn.net/qq_27123591/article/details/80272669
这里有两个具体的例子实现了ARIMA
1.https://machinelearningmastery.com/time-series-forecast-study-python-annual-water-usage-baltimore/
这两个例子介绍了如何根据acf、pacf选择ARIMA的pdq
这里我们用predict实现了ARIMA的滚动预测,也可以手动实现(虽然不必要)可以参考:
https://machinelearningmastery.com/make-manual-predictions-arima-models-python/