Bootstrap

c++数据结构算法复习基础-- 2 -- 线性表-单链表-常用操作接口-复杂度分析

1、链表

特点

每一个节点都是在堆内存上独立new出来的，
节点内存不连续·

优点

内存利用率高，不需要大块连续内存
插入和删除节点不需要移动其它节点，时间复杂度O(1)。
不需要专门进行扩容操作

缺点

内存占用量大，每一个节点多出存放地址的空间。
节点内存不连续，无法进行内存随机访问
链表搜索效率不高，只能从头节点开始逐节点遍历

理解，链表存在的意义

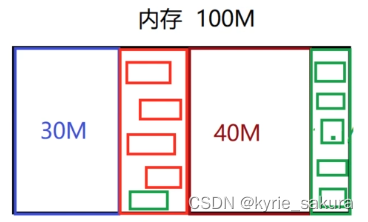
假设下面这个方框代表我们计算机里边的内存，这里假设他只有100兆。
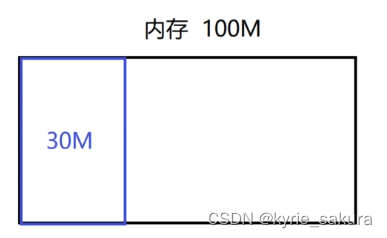
在这里插入图片描述
每一个程序运行以后变成进程，进程在运行的过程中，可能需要有这个分配内存的这么一些操作，那么这块儿内存呢，就被分配出去，多大呢，假设第一次分配30兆。
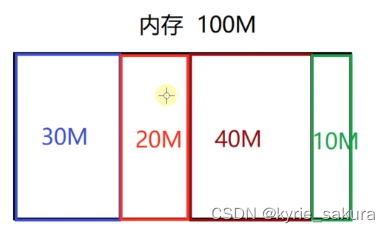
在这里插入图片描述

随着进程的运行，一会儿又有一块内存被分配出去，假设这个是20兆。
随着程序的运行呢，又有一部分内存，分配出去了，这一块儿又有十兆的空间被进程分配走了。
那么现在在这100兆的内存上，这内存都被进程在运行过程中分配走了。
在这里插入图片描述

内存有分配就有释放，那么这个内存它是一块儿一块儿紧挨着分配的，但是他释放，那就不一定是挨紧挨着一个一个释放了。
因为每一个内存都有它所属的应用的一些业务，这业务执行完了，这内存没有用了，他才释放。
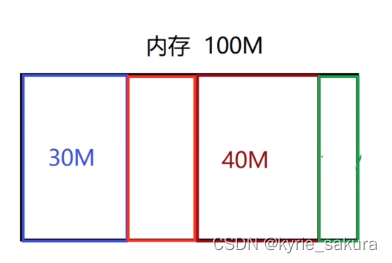
那么这里假设40M的内存所属的这个业务，其直线的周期比较长，所以它释放的就慢。这个红色20M的跟这个绿色10M的这两块内存，他们所属的业务执行比较快，那这块内存就会先于40M释放掉了，我们应用程序都释放掉了，还有交还给系统了。
在这里插入图片描述

此时，就形成了所谓的内存的碎片，堆内存的碎片。
我们这个内存现在剩余空间，看着100兆，应该是有20兆，加上十兆，他是总共有30兆。
如果我们的进程现在运行过程中，他需要一个线性表，来存储一组数据，他需要25兆的空间，但此时我们不能分配一个25兆空间的数组，为什么呢，因为数组要求内存绝对的、连续的，此时内存有空闲，有总共是20兆加10兆，也就是30兆的空间，看起来是可以分配25兆的，但是呢，你分配的是数组内存，他需要25兆内存，完全是连续的内存。此时就存在问题。
我们堆内存在通过malloc或者new来分配的时候，是这样连续分配的。但是呢，不同的内存块儿隶属于不同的业务，那业务执行的周期长短不一样，那么也就是说内存块分配的时候挨个分配，但是释放的时候却不一定是挨个儿释放的，哪个业务执行完了，相应的内存块儿会去释放掉内存，交还给这个系统，所以我们内存上就产生了碎片化。
碎片化导致我们空闲的内存，没有办法连到一块儿。当然了，内核会进行内存碎片的一些整理，过多的细节这里暂时不讨论。总之，此时，我们在内存碎片比较多的情况下，我们去开辟大内存数组的时候，往往容易开辟失败，整个的空闲空间是有，但是连续的这么大的空间，他不一定有。所以此时呢，我们就有了链表它存在的意义。
数组：每一个元素的内存都是连续的，
链表：每一个节点都是独立分配的。
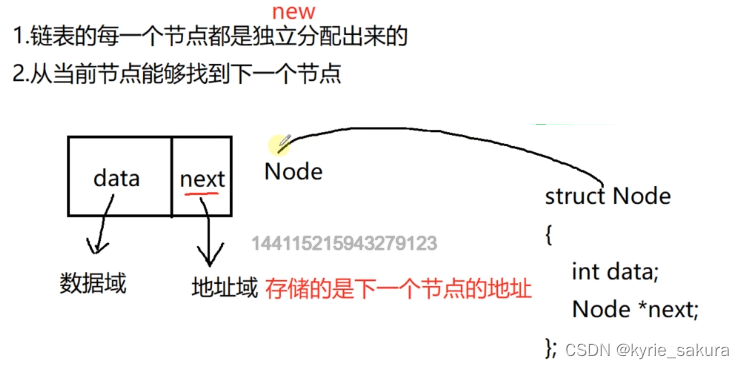
在这里插入图片描述
那么如何将各个独立的节点链接起来的。链表的结构体就设计成这样：
在这里插入图片描述

每个节点分为两部分，一部分称之为数据域，用于保存数据，一部分称之为地址域，用来保存下一个节点的地址。

2、数组和链表的区别

1）数组和链表的定义

数组的定义

数组是一组具有相同数据类型的变量的集合，这些变量称之为集合的元素

每个元素都有一个编号，称之为下标，可以通过下标来区别并访问数组元素，数组元素的个数叫做数据的长度

链表的定义

链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

链表的特性是在中间任意位置插入和删除元素都非常快，不需要移动其它元素

对于单向链表而言，链表中的每一个元素都要保存一个指向下一个元素的指针

对于双向链表而言，链表中的每个元素既要保存指向下一个元素的指针，又要保存指向上一个元素的指针

对于双向循环链表而言，链表中的最后一个元素保存一个指向第一个元素的指针

2）数组和链表的区别

数组链表
（1）数组在内存中连续； (2)使用数组之前，必须事先固定数组长度，不支持动态改变数组大小；(3) 数组元素增加时，有可能会数组越界；(4) 数组元素减少时，会造成内存浪费；（5）数组增删时需要移动其它元素（1）链表采用动态内存分配的方式，在内存中不连续 (2)支持动态增加或者删除元素 (3)需要时可以使用malloc或者new来申请内存，不用时使用free或者delete来释放内存
数组从栈上分配内存，使用方便，但是自由度小链表从堆上分配内存，自由度大，但是要注意内存泄漏
数组在内存中顺序存储，可通过下标访问，访问效率高链表访问效率低，如果想要访问某个元素，需要从头遍历
数组的大小是固定的，所以存在访问越界的风险只要可以申请得到链表空间，链表就无越界风险

3）数组和链表的使用场景

数组使用场景链表使用场景
数组的存储空间是栈上分配的，存储密度大，当要求存储的大小变化不大时，且可以事先确定大小，宜采用数组存储数据链表的存储空间是堆上动态申请的，当要求存储的长度变化较大时，且事先无法估量数据规模，宜采用链表存储
数组访问效率高。当线性表的操作主要是进行查找，很少插入和删除时，宜采用数组结构链表插入、删除效率高，当线性表要求频繁插入和删除时，宜采用链表结构

原文链接：https://blog.csdn.net/weixin_42438797/article/details/115339605

3、单向链表常用操作接口

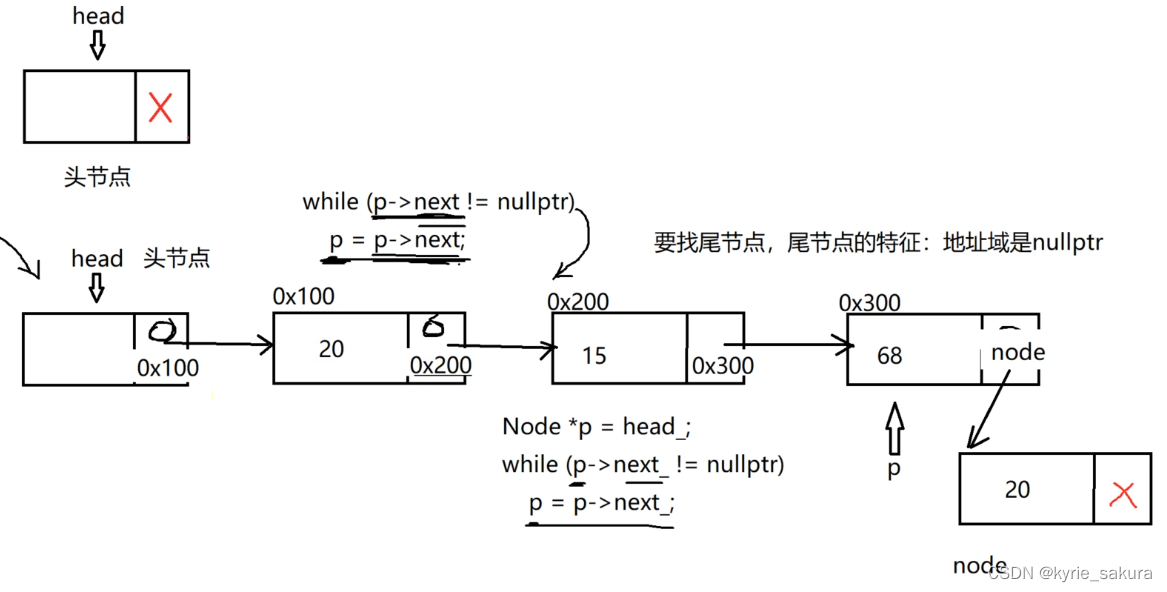
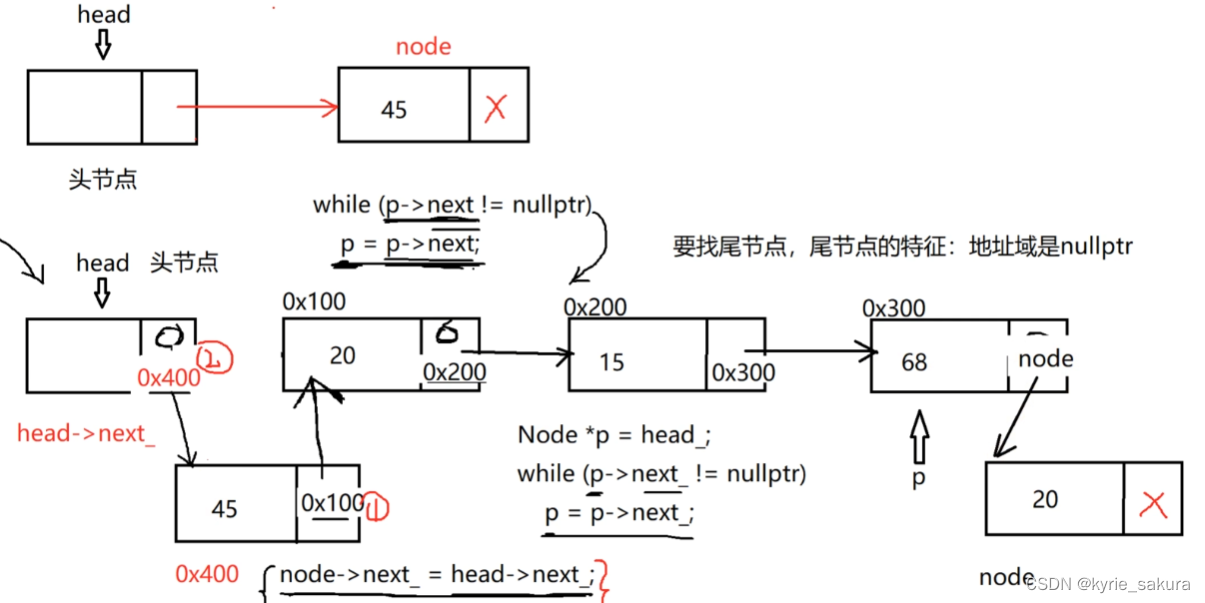
寻找尾结点思路：

先定义一个指针，让它指向头结点，
然后判断当前这个指针指向的结点的next域为不为空（不为空就说明他不是尾节点，为空了就说明他是尾结点，因为链表里边所有节点的地址域都不为空，除了尾节点。）
再遍历链表的每一个节点，让指针P从当前节点，跳到下一个节点，直到尾节点。

节点简单设计

struct Node
{
	Node(int data=0):data_(data),next_(nullptr){}
	int data_;
	Node* next_;
};

1）构造函数

Clink()
	{
		//给head_初始化指向头节点
		head_ = new Node();
	}

2）析构函数

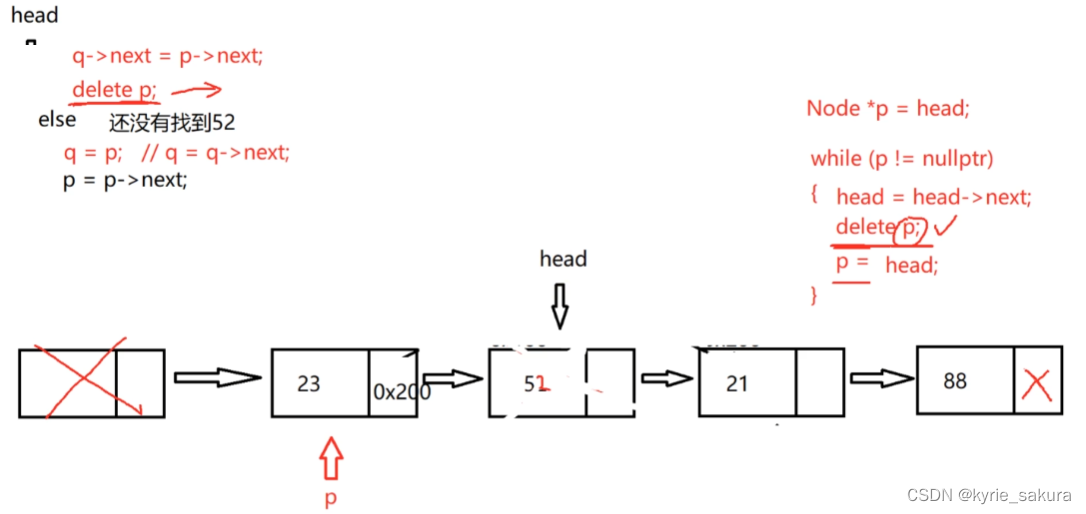
思路图：

在这里插入图片描述

代码实现

	~Clink()
	{
		//节点的释放

		//错误示例
		//delete []head_;//链表不连续
		//head_ = nullptr;

		Node* p = head_;
		while(p != nullptr)
		{
			head_ = head_->next_;
			delete p;
			p = head_;
		}
		head_ = nullptr;
	}

3）尾插

思路图：

在这里插入图片描述

代码实现

	//链表的尾插法 O(n)
	void InsertTail(int val)
	{
		//先找到当前链表的末尾节点
		Node* p = head_;
		while(p->next_ != nullptr)
		{
			p = p->next_;
		}
		//生成新节点
		Node* node = new Node(val);
		//把新节点挂在尾节点的后面
		p->next_ = node;
	}

4）头插

思路图：

在这里插入图片描述

代码实现

	//链表的头插法 O(1)
	void InsertHead(int val)
	{
		Node* node = new Node(val);
		node->next_ = head_->next_;
		head_->next_ = node;

	}

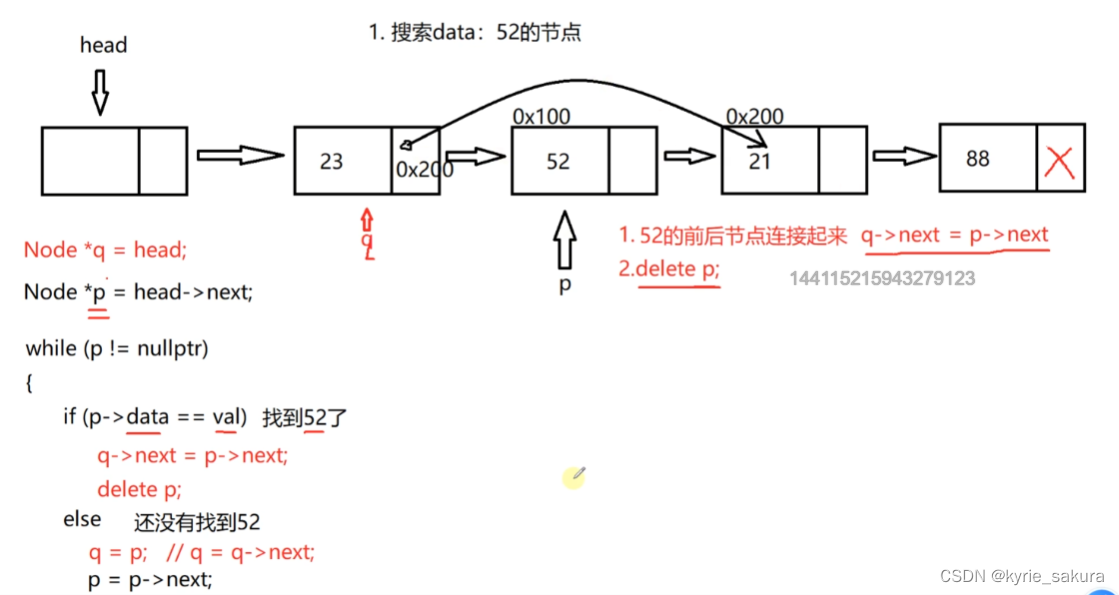
5）链表的删除

删除第一个符合条件的节点：

思路图：
在这里插入图片描述
代码实现：

//链表节点的删除  O(n) + O(1)
	void Remove(int val)//这里删除值val的第一个节点
	{
		Node *p = head_;

		while(p->next_ != nullptr)
		{
			if(p->next_->data_ == val)
			{
				Node *q = p->next_;
				p->next_ = p->next_->next_;
				delete(q);
				return;//删除第一个
			}
			else
			{
				p=p->next_;
			}
			
		}
		/*
		Node *q = head_;
		Node *p = head_->next_;
		while(p != nullptr)
		{
			if(p->data_ == val)
			{
				q->next_ = p->next_;
				delete p;
				return;//删除第一个
			}
			else
			{
				q = p;
				p = p->next_;
			}
			
		}*/
	}

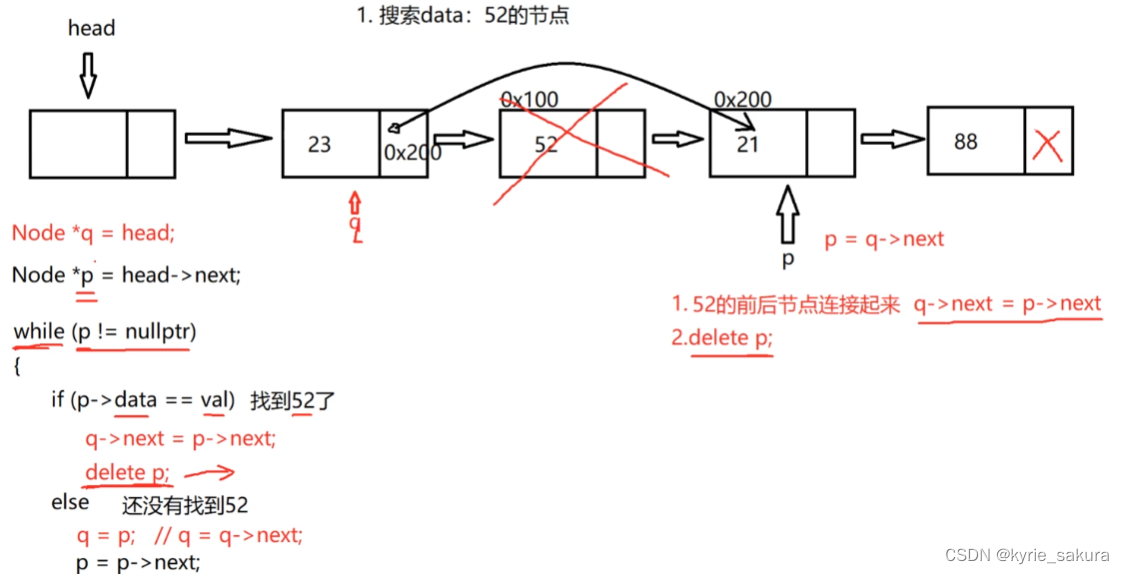
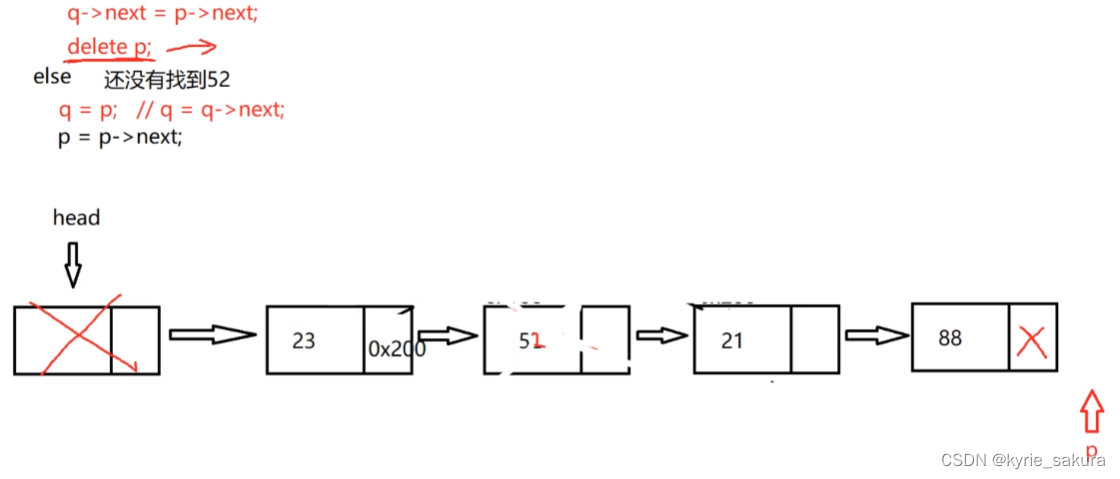
删除所有符合条件的节点：

思路图：
在这里插入图片描述
代码实现：

void RemoveALL(int val)//这里删除值val的所有节点
	{
		Node *p = head_;

		while(p->next_ != nullptr)
		{
			if(p->next_->data_ == val)
			{
				Node *q = p->next_;
				p->next_ = p->next_->next_;
				delete(q);
				//return;//删除第一个
			}
			else
			{
				p=p->next_;
			}
			
		}
		/*
		Node *q = head_;
		Node *p = head_->next_;
		while(p != nullptr)
		{
			if(p->data_ == val)
			{
				q->next_ = p->next_;
				delete p;
				//对指针p进行重置
				p = q->next_;
			}
			else
			{
				q = p;
				p = p->next_;
			}
			
		}*/
	}

6）单链表的搜索接口简单实现

链表搜索 list O(n)
区别于
数组的下标访问/随机访问 O(1) 搜索 O(n)

思路图

在这里插入图片描述

代码实现：

	//链表搜索 list O(n) 区别于数组的下标访问/随机访问 O(1)  搜索 O(n)
	bool Find(int val)//这里返回bool
	{
		Node* p = head_->next_;
		while(p != nullptr)
		{
			if(p->data_ == val)
			{
				return true;
			}
			else
			{
				p = p->next_;
			}
		}
		return false;
	}

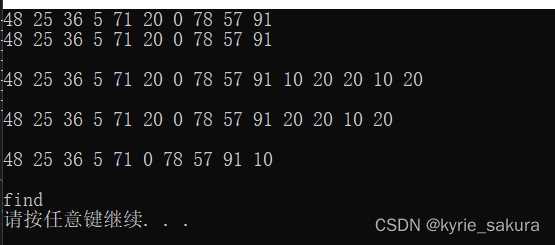
7）测试，以及完整代码

单链表接口简单实现

#include <iostream>
#include <stdlib.h>
#include <time.h>
#include <string.h>
using namespace std;

//节点类型
struct Node
{
	Node(int data=0):data_(data),next_(nullptr){}
	int data_;
	Node* next_;
};

//单链表代码实现
struct Clink
{
public:
	Clink()
	{
		//给head_初始化指向头节点
		head_ = new Node();
	}
	~Clink()
	{
		//节点的释放

		//错误示例
		//delete []head_;//链表不连续
		//head_ = nullptr;

		Node* p = head_;
		while(p != nullptr)
		{
			head_ = head_->next_;
			delete p;
			p = head_;
		}
		head_ = nullptr;
	}

public:
	//链表的尾插法 O(n)
	void InsertTail(int val)
	{
		//先找到当前链表的末尾节点
		Node* p = head_;
		while(p->next_ != nullptr)
		{
			p = p->next_;
		}
		//生成新节点
		Node* node = new Node(val);
		//把新节点挂在尾节点的后面
		p->next_ = node;
	}
	//链表的头插法 O(1)
	void InsertHead(int val)
	{
		Node* node = new Node(val);
		node->next_ = head_->next_;
		head_->next_ = node;

	}
	//链表节点的删除
	void Remove(int val)//这里删除值val的第一个节点
	{
		Node *p = head_;

		while(p->next_ != nullptr)
		{
			if(p->next_->data_ == val)
			{
				Node *q = p->next_;
				p->next_ = p->next_->next_;
				delete(q);
				return;//删除第一个
			}
			else
			{
				p=p->next_;
			}
			
		}
		/*
		Node *q = head_;
		Node *p = head_->next_;
		while(p != nullptr)
		{
			if(p->data_ == val)
			{
				q->next_ = p->next_;
				delete p;
				return;//删除第一个
			}
			else
			{
				q = p;
				p = p->next_;
			}
			
		}*/
	}

	void RemoveALL(int val)//这里删除值val的所有节点
	{
		Node *p = head_;

		while(p->next_ != nullptr)
		{
			if(p->next_->data_ == val)
			{
				Node *q = p->next_;
				p->next_ = p->next_->next_;
				delete(q);
				//return;//删除第一个
			}
			else
			{
				p=p->next_;
			}
			
		}
		/*
		Node *q = head_;
		Node *p = head_->next_;
		while(p != nullptr)
		{
			if(p->data_ == val)
			{
				q->next_ = p->next_;
				delete p;
				//对指针p进行重置
				p = q->next_;
			}
			else
			{
				q = p;
				p = p->next_;
			}
			
		}*/
	}
	//搜索 list O(n)
	bool Find(int val)//这里返回bool
	{
		Node* p = head_->next_;
		while(p != nullptr)
		{
			if(p->data_ == val)
			{
				return true;
			}
			else
			{
				p = p->next_;
			}
		}
		return false;
	}
	
	//链表打印
	void show()
	{
		Node *p = head_->next_;
		//while(p->next != nullptr) //error
		while(p != nullptr)
		{
			cout<< p->data_ << " ";
			p=p->next_;
		}
		cout << endl;
	}

private:
	Node* head_;//指向链表的头节点
};

测试用例

int main()
{
	Clink link;
	srand(time(0));
	for(int i = 0; i<10; i++)
	{
		int val = rand() % 100;
		link.InsertTail(val);
		cout << val << " ";
	}
	cout << endl;

	//测试头插
	link.show();
	cout << endl;

	//测试尾插
	link .InsertTail(10);
	link .InsertTail(20);
	link .InsertTail(20);
	link .InsertTail(10);
	link .InsertTail(20);
	link.show();
	cout << endl;

	//测试删除第一个节点
	link.Remove(10);
	link.show();
	cout << endl;

	//测试删除所有节点
	link.RemoveALL(20);
	link.show();
	cout << endl;

	//测试搜索
	if(link.Find(10))
	{
		cout <<"find"<<endl;
	}
	else
	{
		cout <<"false"<<endl;
	}

}

运行结果：

在这里插入图片描述

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
基于ssm的医院分诊系统
Java中的for-each（增强的for循环）
Flask模板_循环结构
C/C++从入门到精通
U8glib学习使用（详细版）
【Redis x Spring】使用 SCAN 命令搜索缓存
基于SpringBoot搭建应用开发框架(二) —— 登录认证
GIT--克隆MR（还没合入）目标分支代码+增量代码
vue3父组件使用子组件方法
【OpenAI】第二节（Token）什么是Token?如何计算ChatGPT的Token?
;