代码

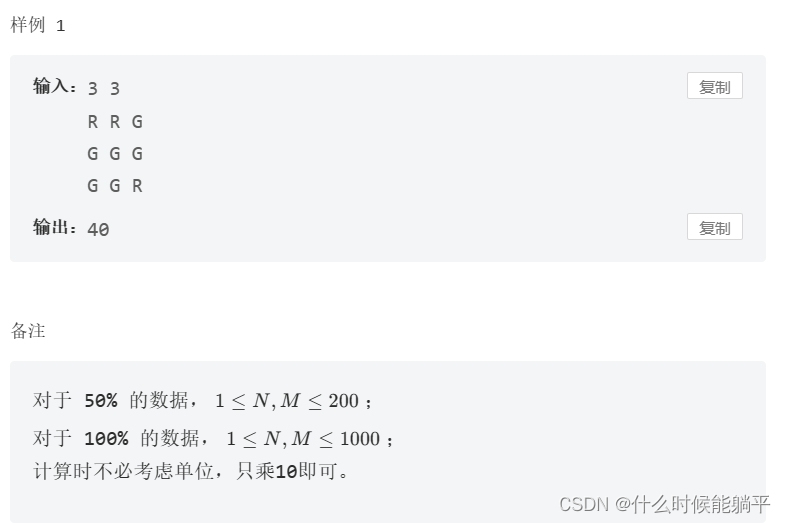
1.暴力7/15：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e6 + 10;
int n, m;
char mp[1005][1005];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> mp[i][j];
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; i++) // 暴力枚举
    {
        for (int j = 1; j <= m; j++)
        {
            if (mp[i][j] == 'G') // 找到左上角是G的点
            {
                for (int k = i; k <= n; k++)
                {
                    for (int l = j; l <= m; l++)
                    {
                        int flag = 1;                // flag是标记是否有R
                        for (int x = i; x <= k; x++) // i k j l是矩形的左上,右上,左下,右下
                        {
                            for (int y = j; y <= l; y++)
                            {
                                if (mp[x][y] == 'R')
                                {
                                    flag = 0;
                                    break;
                                }
                            }
                            if (flag == 0)
                            {
                                break;
                            }
                        }
                        if (flag == 1)
                        {
                            ans = max(ans, (k - i + 1) * (l - j + 1));
                        }
                    }
                }
            }
        }
    }
    cout << ans * 10;
}

2.单调栈15/15

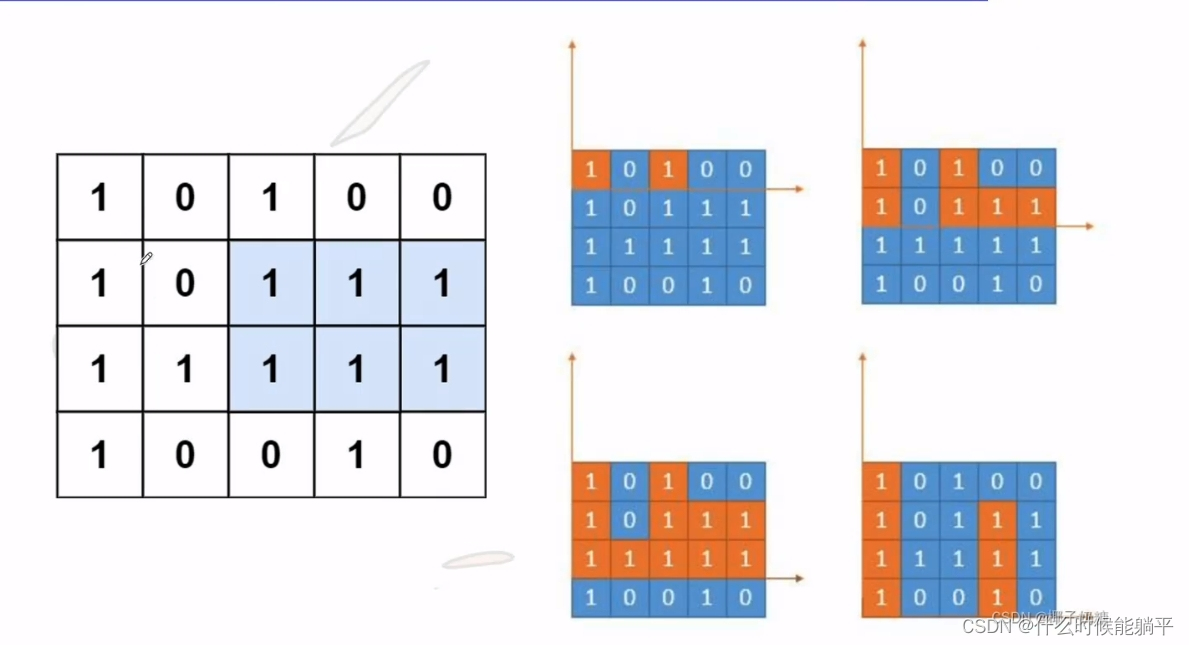
矩阵可以根据不同的行看成直方图： 

（图源b站up主：轩哥码题） 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e3 + 10;
int n, m, a[N][N], ans;
char ch;
// 单调栈，找右边第一个比自己小的数
// 栈顶元素>=要进来的元素：栈顶元素出栈
// 如果有元素出栈，则右边界为要进来的元素位置，左边界为栈中上一个元素位置
// 将二维平面看成不同的一维数组，对每一行进行单调栈操作
int maxRec(int x)
{ // 使用单调栈求某行作为x轴的最大矩形面积
    int ret = 0;
    stack<int> s;
    s.push(0);
    for (int i = 1; i <= m + 1; i++) // i:位置
    {
        while (a[x][i] < a[x][s.top()]) // 如果有元素出栈
        {
            int h = a[x][s.top()];
            s.pop();
            int w = i - s.top() - 1; // 宽度
            ret = max(ret, w * h);
        }
        s.push(i);
    }
    return ret;
}
int main()
{

    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> ch;
            if (ch == 'G')
                a[i][j] = 1;
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if (a[i][j])//a[i][j]是G，才算有效
                a[i][j] += a[i - 1][j];
        }
    }
    for (int i = 1; i <= n; i++)
    {
        ans = max(ans, maxRec(i));
    }
    cout << ans * 10;
    return 0;
}

3.动态规划15/15

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
int n, m;
char aij;
ll sum[1005][1005], ans, temp;
// 动态规划，将二维转为一维
// 思路：R点设为负无穷大，二维用前缀和转移成一维，求一维的最大连续子序列
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> aij;
            if (aij == 'R')
                temp = -INF;
            else
                temp = 10;
            sum[i][j] = sum[i - 1][j] + temp;
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = i; j <= n; j++)
        {
            ll sum1 = 0;
            for (int k = 1; k <= m; k++)
            {
                sum1 += sum[j][k] - sum[i - 1][k];
                if (sum1 < 0)
                {
                    sum1 = 0;
                }
                ans = max(ans, sum1);
            }
        }
    }
    cout << ans;
}