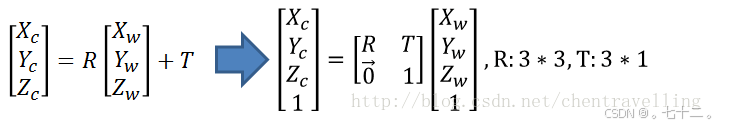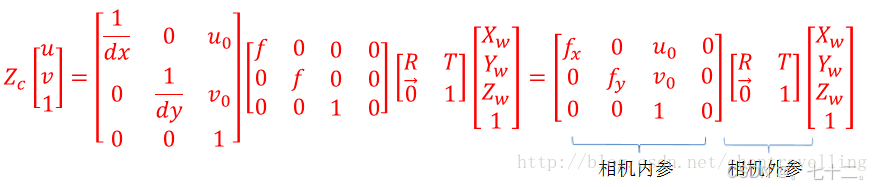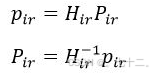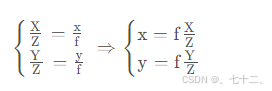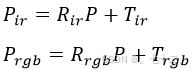kinect 2.0 SDK学习笔记(四)--深度图与彩色图对齐_mapdepthframetocolorspace-CSDN博客
相机标定(三)-相机成像模型_相机小孔成像模型-CSDN博客
1.原理部分
立体视觉往往会设计到:世界坐标系、相机坐标系、图像坐标系和像素坐标系。
世界坐标系是为了更好的描述相机的位置,双目立体视觉中一般将世界坐标系原点定在左相机或者右相机又或者两者x轴方向的中点。
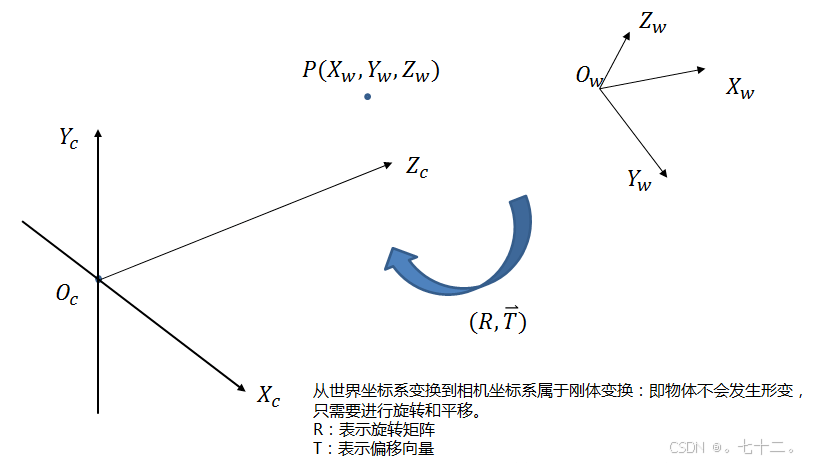
①首先从世界坐标系到相机坐标系
世界坐标系中的某一个点通过平移旋转可以获得相机坐标系的位置。
详细推理请看第一篇博客。
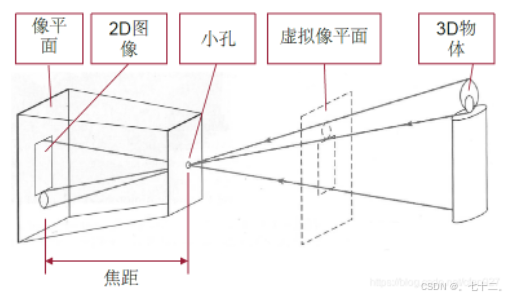
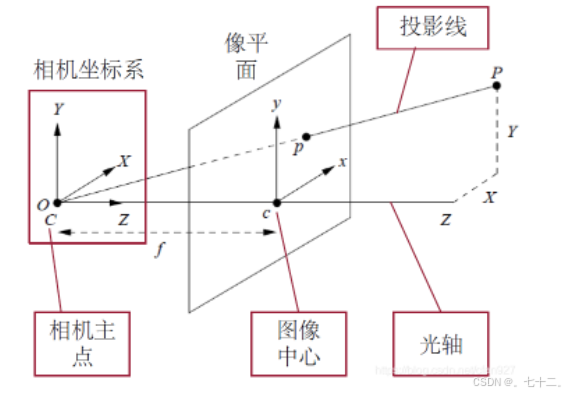
②从相机坐标系到图像坐标系,透视变换,从3d到2d,投影点的单位是mm,将它转换到像素坐标系单位才会变成pixel。
图像坐标系的原点为相机光轴与成像平面的交点,通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm,属于物理单位,而像素坐标系的单位是pixel。
一个三维中的坐标点,的确可以在图像中找到一个对应的像素点,但是反过来,通过图像中的一个点找到它在三维中对应的点就很成了一个问题,因为我们并不知道等式左边的Zc的值。
2.深度图和彩色图的配准
深度图和彩色图的配准又叫对齐,之所以需要进行配准,是因为深度图中的坐标点是在深度相机坐标系下获得,彩色图的坐标点是在RGB相机坐标系下获得的。
需要先使用张正友标定等标定法,对深度相机和RGB相机分别进行标定,获得相机的内外参矩阵。
设P_ir为在深度摄像头坐标下某点的空间坐标,p_ir为该点在像平面上的投影坐标(x、y单位为像素,z等于深度值,单位为毫米),H_ir为深度摄像头的内参矩阵,由小孔成像模型可知:(公式一)
小孔成像模型实际上是透视投影(perspective projection)的一种最简单的形式。假设我们要将真实世界中的三维点( X , Y , Z ) 投影为二维图像上的点p = ( x , y ) 则有:
设P_rgb为在RGB摄像头坐标下同一点的空间坐标,p_rgb为该点在RGB像平面上的投影坐标,H_rgb为RGB摄像头的内参矩阵。由于深度摄像头的坐标和RGB摄像头的坐标不同,他们之间可以用一个旋转平移变换联系起来,即:(公式二)
其中R为旋转矩阵,T为平移向量。最后再用H_rgb对P_rgb投影,即可得到该点对应的RGB坐标(空间坐标到像素坐标的关系):(公式三)
p_ir和p_rgb使用的都是齐次坐标,在构造p_ir时,应将原始的像素坐标(x,y)乘以深度值,而最终的RGB像素坐标必须将p_rgb除以z分量,即(x/z,y/z),且z分量的值即为该点到RGB摄像头的距离(单位为毫米)。
如何求联系两个坐标系的旋转矩阵和平移向量。这就要用到摄像头的外参了。
外参矩阵实际上也是由一个旋转矩阵R_ir(R_rgb)和平移向量T_ir(T_rgb)构成的,它表示将一个世界坐标系下的点P变换到摄像头坐标系下,分别对深度摄像头和RGB摄像头进行变换,有以下关系:(公式四) 世界坐标系与相机坐标系的关系,用到外参矩阵。
上式中先将P用P_ir、R_ir和T_ir的表达式表示,再代入第二个公式,可得:
上式可以看出,这是在将P_ir变换为P_rgb,对比之前的式子:
可以求出:
这就是最终两个深度相机坐标系和RGB坐标系之间的坐标转换关系,就是博客三中获得的关系式,但是当时看他的博客,没看懂它是怎么出来的公式,现在才明白。建议大家看第二篇博客更好懂一点,但是每个人理解能力不一样,说不定有的人看第三篇更好懂,个人看法。
小孔成像模型:
因此,我们只需在同一场景下,得到棋盘相对于深度摄像头和RGB摄像头的外参矩阵,即可算出联系两摄像头坐标系的变换矩阵(注意,所有旋转矩阵都是正交阵,因此可用转置运算代替求逆运算)。虽然不同场景下得到的外参矩阵都不同,计算得到的R和T也有一些变化。
import cv2
import numpy as np
import oppenni as opp
from openni import openni2
dframe_data = cv2.imread('depth.png',)
frame = cv2.imread('frame.png')#
#dframe_data = np.array(frame.get_buffer_as_triplet()).reshape([480, 640, 2])
dpt1 = np.asarray(dframe_data[:, :, 0], dtype='float32')
dpt2 = np.asarray(dframe_data[:, :, 1], dtype='float32')
dpt2 *= 255
#对于为什么要乘于255的解答
#深度图像的深度值 是按照16位长度(两字节)的数据格式存储的,也可以认为前八位是高字节,后八位是低字节。
#因此一张深度图像如果是 640480分辨率的话,那么图像字节大小 就是 640480*2,其中一个字节是8位(255)
# 乘以 255 是为了将低字节部分从0-255的范围转换到0-65535的范围,这样就可以与高字节部分相加得到完整的16位深度值
dpt = dpt1 + dpt2
#cv2里面的函数,就是类似于一种筛选
'假设我们需要让我们的深度摄像头感兴趣的距离范围有差别地显示,那么我们就需要确定一个合适的alpha值,公式为:有效距离*alpha=255,' \
'假设我们想让深度摄像头8m距离内的深度被显示,>8m的与8m的颜色显示相同,那么alpha=255/(8*10^3)≈0.03,' \
'假设我们想让深度摄像头6m距离内的深度被显示,>6m的与6m的颜色显示相同,那么alpha=255/(6*10^3)≈0.0425'
cv2.imshow('depth_src', dpt)
dim_gray = cv2.convertScaleAbs(dpt, alpha=0.17)
#对深度图像进行一种图像的渲染,目前有11种渲染方式,大家可以逐一去试下
depth_colormap = cv2.applyColorMap(dim_gray, 2) # 有0~11种渲染的模式
cv2.imshow('depth', depth_colormap)
ret, frame = cap.read()
cv2.imshow('color', frame)
key = cv2.waitKey(1)
if int(key) == ord('q'):
break
# rgb相机的内参矩阵(旋转矩阵 平移矩阵) 相机坐标系到图像坐标系
RK_rgb = np.array([(0.999993, 0.00372933, -0.000414306), (-0.00372927, 0.999993, 0.000135122), (0.000414807, -0.000133576, 1)])
#TK_rgb = np.array([-0.0148581, -8.0544e-05, 2.60393e-05])
# 深度相机的内参矩阵
RK_dep = np.array([(0.999993, 0.00372933, -0.000414306), (-0.00372927, 0.999993, 0.000135122), (0.000414807, -0.000133576, 1)])
#TK_dep = np.array([-0.0148581, -8.0544e-05, 2.60393e-05])
# rgb相机的外参矩阵(旋转矩阵 平移矩阵) 世界坐标系到相机坐标系
R_rgb = np.array([(0.999993, 0.00372933, -0.000414306), (-0.00372927, 0.999993, 0.000135122), (0.000414807, -0.000133576, 1)])
T_rgb = np.array([-0.0148581, -8.0544e-05, 2.60393e-05])
# 深度相机的外参矩阵
R_dep = np.array([(0.999993, 0.00372933, -0.000414306), (-0.00372927, 0.999993, 0.000135122), (0.000414807, -0.000133576, 1)])
T_dep = np.array([-0.0148581, -8.0544e-05, 2.60393e-05])
Rir_rgb = np.dot(R_rgb @ np.linalg.inv(R_dep)) # 两个相机坐标系之间的变换矩阵
Tir_rgb = [email protected](R_dep)@T_dep
R = RK_rgb@[email protected](RK_dep) # 像素点之间的变换关系矩阵
T = RK_rgb@Tir_rgb
# 形状
result = np.zeros((dpt.shape[0], dpt.shape[1], 3), dtype=np.uint8)
i = 0
# 遍历的深度图 深度图在rgb图上对齐 找到对应的像素点
for row in range(dpt.shape[0]):
for col in range(dpt.shape[1]):
depth_value = dpt[row, col] # 获取深度值
if depth_value != 0 and depth_value != 65535:
# 投影到彩色坐标系上的坐标
uv_depth = np.array([col, row, 1.0]) # 齐次坐标
uv_color = depth_value / 1000.0 * np.dot(R, uv_depth) + T / 1000.0 # Z_rgb*p_rgb=R*Z_ir*p_ir+T;; (除以1000,是为了从毫米变米) 深度坐标系下的其次标点加上旋转平移获得egb坐标系下的点
print("uv_color is:", uv_color, '\n', uv_color.shape)
X = int(uv_color[0] / uv_color[2]) # 除以齐次坐标的最后一个元素获得像素值
Y = int(uv_color[1] / uv_color[2]) # // Z_rgb*p_rgb -> p_rgb
if 0 <= X < frame.shape[0] and 0 <= Y < frame.shape[1]:
result[row, col] = frame[Y, X]
else:
result[row, col] = [0, 0, 0]
i += 1
cv2.imwrite(save_path+'registrationResult.png', result)
cv2.imwrite(save_path+'src_depth.png', dpt)
cv2.imwrite(save_path+'color_depth.png', depth_colormap)
cv2.imwrite(save_path+'rgb.png', frame) 代码是根据其他博客和相关技术写的,还未进行测试,如果有什么问题,大家可以提出来,马上修改。