Bootstrap

详细说说布隆过滤器 BloomFilter

文章目录

1. 什么是布隆过滤器

布隆过滤器（Bloom Filter）是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数，可以用于检索一个元素是否在一个集合中。

上面这句话的核心就是布隆过滤器可以判断一个元素是否存在，没有使用布隆过滤器之前，假设我们要判断手机号码在不在一个集合里面，最常见的方法就是使用 HashSet 把
所有的手机号都存起来，判断的时候通过 set.contains(key) 来判断，但是这样就会有一个问题，如果我需要判断存储的号码总数超过 1000w，假设一个手机号码 11 位，计算如下：

  • 假设手机号码都使用 String 来存储，一个字符是 2 个字节，那么就需要花费 2 * 11 * 1000w ≈ 210 MB ≈ 0.205 GB
  • 上面的计算过程只是单单计算了字符的占用，实际上一个 String 对象在 JVM 中的存储包括对象头、填充等数据，同时 HashMap 中 Node 的节点数据、指针数据等加起来远不止 210 MB

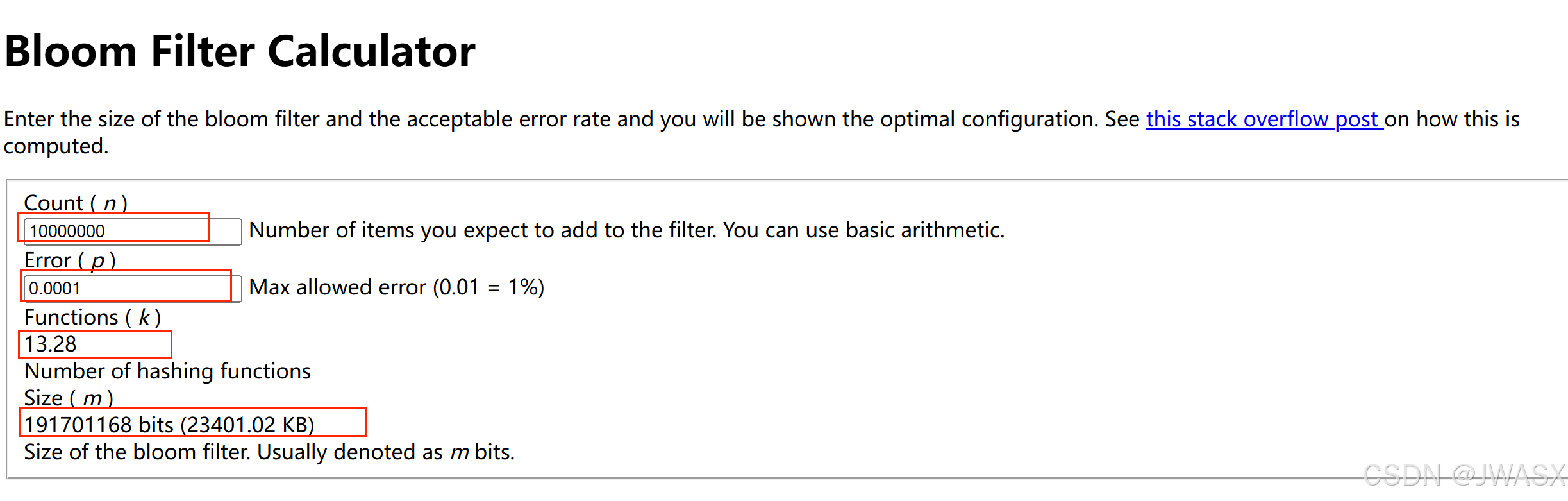
所以可以到这里就可以看到传统的 Set 集合存储 1000W 的字符串要花费的空间是比较多的，这部分数据也不可能存在 Set 里面，对于布隆过滤器，有一个网站就提供了计算内存的能力：布隆过滤器在线计算内存
在这里插入图片描述

从图中可以看到，往 BloomFilter 插入 10000000w 的数据，误差率为 0.01% 的前提下，总共只需要 22.85MB 的内存，但是同样的误差率也有 0.01，什么意思呢？意思是在 1000w 数据的布隆过滤器里面去搜索数据是否存在，假设我有 100w 条数据，经过搜索之后，会有差不多 100 条数据原本不在布隆过滤器里面，但是结果缺失已存在

所以布隆过滤器有以下几个优点：

  • 以极少的内存存储大量的数据
  • 插入和查询的时间都是常数级别（主要时间花费在 Hash 的计算）
  • 不存储数据本身，在需要对数据保密的场合有优势

同时布隆过滤器的缺点也很明显：

  • 极低的内存意味者会有误差率，想要误差率变低，可以使用可删除的布隆过滤器 Counting，但是这样就意味着空间使用需要增加
  • 至于为什么有误判，比如 hash(str1)和 hash(str2)都指向同一个 bit 自然就冲突了，这时候就会误判

2. 原理

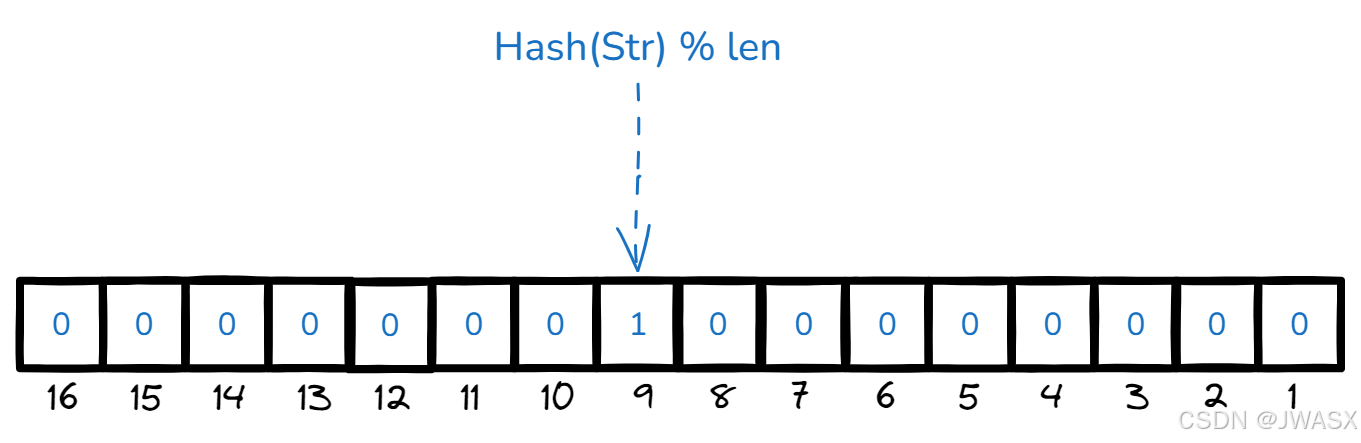
布隆过滤器的原理：通过一个Hash函数将一个元素映射成一个位阵列（Bit array）中的一个点，只需要把这个 bit 设置成 1，就可以通过直接判断这个 bit 来判断元素是否存在
在这里插入图片描述

比如上面这个例子，通过 Hash(Str) 求出第 9 位，那么把第 9 位标记为 1，下次查询的时候一样通过这个位就能判断 Str 字符串在不在 BloomFilter 里面

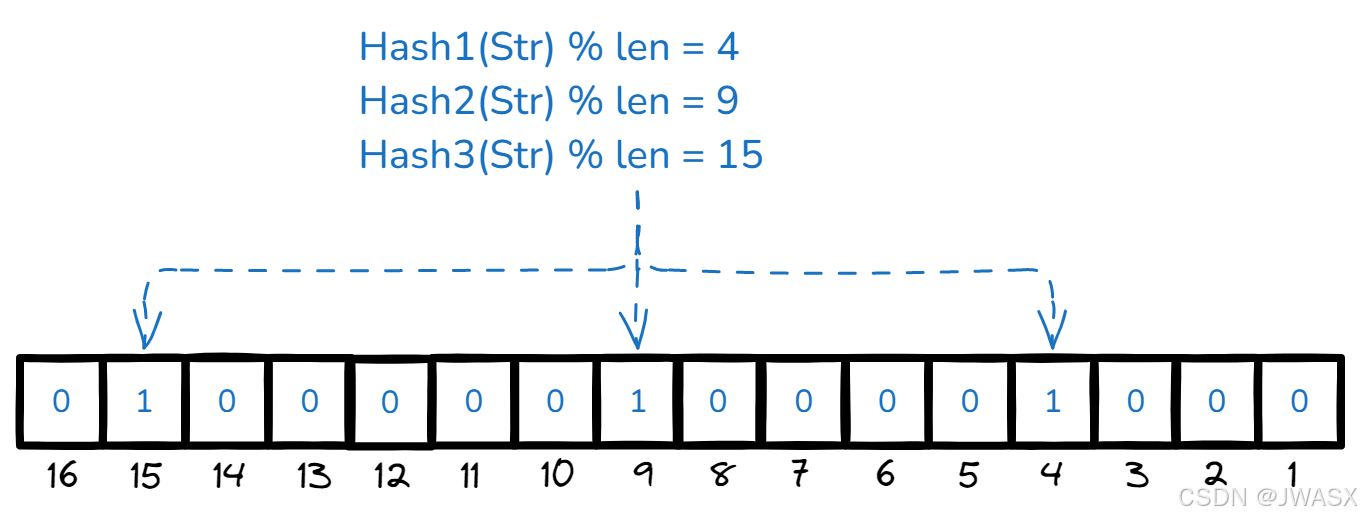
不过看上面的例子也不难发现了，最主要的问题就是 Hash 冲突，假设这个 Hash 函数求出的位足够分散，如果我们一共有 m 个 bit，需要将冲突降到 0.01，也就是说这个散列表只能容纳 m / 100 个元素，这个空间利用率就太低了，解决方法就是多增加几个 hash 函数，分别通过这几个 hash 函数求出 Hash(str) 的值，再设置到位数组中，这时候就能大大降低冲突的概率
在这里插入图片描述
但是这样一来就有两个问题：

  1. bit 数组的长度要设置成多少
  2. 要设置多少个 hash 函数

2.1 误差率求导过程

带着上面这两个问题，我们来看下误差率是怎么算出来的，假设 Hash 函数是足够均匀的，也就是说经过这个 Hash 函数 hash 之后映射到每一位的概率都是相同的，现在我们设置几个变量

  1. bit 数组长度 m（一共有多少个 bit）
  2. hash 函数的个数 k
  3. 需要插入的元素个数 n

由于 hash 分布足够均匀，所以每一个元素经过 hash 之后插入 bit 中的概率都是 1 m \frac{1}{m} m1​，我们要求的是误判率，也就是说给定一个字符串，经过 k 次 hash 之后求出来的 bit 的位都是 1。对于一个 bit，hash 一次之后不为 1 的概率是 1 − 1 m 1 - \frac{1}{m} 1−m1​，hash k 次之后不为 1 的概率是：
( 1 − 1 m ) k \begin{gather*} \left( 1 - \frac{1}{m} \right)^k \end{gather*} (1−m1​)k​
m 是 bit 数组长度，所以当 m -> ∞ 的时候，根据极限公式：
lim ⁡ x → ∞ ( 1 − 1 m ) m = 1 e \begin{gather*} \lim_{x \to \infty} \left( 1 - \frac{1}{m} \right)^m = \frac{1}{e}\end{gather*} x→∞lim​(1−m1​)m=e1​​
把 m 用 k 代替，这时候就是
lim ⁡ x → ∞ ( 1 − 1 m ) k = lim ⁡ x → ∞ ( ( 1 − 1 m ) m ) k m = ( 1 e ) k m \begin{gather*} \lim_{x \to \infty} \left( 1 - \frac{1}{m} \right)^k = \lim_{x \to \infty} \left( \left( 1 - \frac{1}{m} \right)^m \right)^{\frac{k}{m}} = \left( \frac{1}{e} \right)^{\frac{k}{m}} \end{gather*} x→∞lim​(1−m1​)k=x→∞lim​((1−m1​)m)mk​=(e1​)mk​​
上面是添加一个元素不为 1 的概率，那么添加了 n 个 元素之后某个位是为 1 概率就是：
1 − ( 1 − 1 m ) k n ≈ 1 − e − k n m \begin{gather*} 1 - \left( 1 - \frac{1}{m} \right)^{kn} \approx 1 - e^{\frac{-kn}{m}} \end{gather*} 1−(1−m1​)kn≈1−em−kn​​
现在得到了添加 n 个元素之后某个位是 1 的概率，然后我们需要查询一个不存在的元素，但是这个元素要经过 k 次计算，并且这 k 次计算对应的每一位都是 1，那么概率就是：
f ( k ) = ( 1 − e − k n m ) k \begin{gather*} f(k) = \left(1 - e^{\frac{-kn}{m}}\right)^k \end{gather*} f(k)=(1−em−kn​)k​
到这里我们就得到了 hash 函数个数（k）和误判率（f(k)）的函数，我们可以看到，因为 n 和 m 都是常数，为了方便计算，就用 t = e − n m t=e^{\frac{-n}{m}} t=em−n​，最终得到式子：
f ( k ) = ( 1 − t k ) k \begin{gather*} f(k) = \left(1 - t^k\right)^k \end{gather*} f(k)=(1−tk)k​
对这个式子求导：
d d t ( 1 − t k ) k = d d t ( e k l n ( 1 − t k ) ) = d d t ( e k l n ( 1 − t k ) ( l n ( 1 − t k ) − k t k l n t 1 − t k ) ) \begin{gather*} \frac{d}{dt} \left(1 - t^k \right)^k =\frac{d}{dt} \left(e^{kln(1-t^k)} \right)=\frac{d}{dt} \left(e^{kln(1-t^k)}(ln(1-t^k) -\frac{kt^klnt}{1-t^k})\right) \end{gather*} dtd​(1−tk)k=dtd​(ekln(1−tk))=dtd​(ekln(1−tk)(ln(1−tk)−1−tkktklnt​))​
令这个式子等于 0，求出来：
t k = 1 2 \begin{gather*} t^k = \frac{1}{2} \end{gather*} tk=21​​
也就是说：
e − k n m = 1 2 \begin{gather*} e^{\frac{-kn}{m}}=\frac{1}{2} \end{gather*} em−kn​=21​​
最后求得：
k = m n l n 2 \begin{gather*} k=\frac{m}{n}ln2 \end{gather*} k=nm​ln2​
也就说 k = m n l n 2 k=\frac{m}{n}ln2 k=nm​ln2 的时候误差函数 f ( k ) = ( 1 − t k ) k f(k) = \left(1 - t^k\right)^k f(k)=(1−tk)k 求得极值

  • 当 k ϵ ( 0 , m n l n 2 ) k \epsilon (0, \frac{m}{n}ln2) kϵ(0,nm​ln2) 时， d d t < 0 \frac{d}{dt} < 0 dtd​<0；
  • 当 k ϵ ( m n l n 2 , + ∞ ) k \epsilon (\frac{m}{n}ln2, +\infty ) kϵ(nm​ln2,+∞) 时， d d t > 0 \frac{d}{dt} > 0 dtd​>0；

所以误差在 k = m n l n 2 k=\frac{m}{n}ln2 k=nm​ln2 的时候求得最小值，把 k 带入原来的式子，求得最小值 p：
p = ( 1 − e − k n m ) k = ( 1 − 1 2 ) m n ln ⁡ 2 = 2 − m n ln ⁡ 2 \begin{gather*} p = \left(1 - e^{\frac{-kn}{m}}\right)^k = \left(1 - \frac{1}{2}\right)^{\frac{m}{n} \ln 2} = 2^{-\frac{m}{n} \ln 2} \end{gather*} p=(1−em−kn​)k=(1−21​)nm​ln2=2−nm​ln2​

好了，现在 p（期望的误判率） 是已知的，n（需要插入的数据个数）也是已知的，这下就可以求出 m（总的 bit 位数）了:
m = − n ∗ l n p ( l n 2 ) 2 \begin{gather*} m=\frac{-n*lnp}{(ln2)^2} \end{gather*} m=(ln2)2−n∗lnp​​

2.2 函数个数和 bit 数组长度

根据上面的公式求导过程，我们知道：
b i t 数组长度 = m = − n ∗ l n p ( l n 2 ) 2 h a s h 函数个数 k = m n l n 2 \begin{gather*} bit 数组长度 = m=\frac{-n*lnp}{(ln2)^2} \newline\newline hash 函数个数 k=\frac{m}{n}ln2 \end{gather*} bit数组长度=m=(ln2)2−n∗lnp​hash函数个数k=nm​ln2​
有了这两个公式就能初始化 BloomFilter 了，但是现在问题又来了，hash 函数从哪找？k = 2、3 比较小的数字的时候还是容易找的，但是 k 如果等于几十个，哪里找这么多 hash 函数呢

2.3 hash函数

可以使用双 hash 来求出 k 个 hash 值，计算公式：f[i] = a(δ) + i * b(δ) (mod m)
在具体源码中也是通过这个方法来计算的，下面讲到源码再细说

3. 使用

Maven 引入 Google 的 guava 包

    <dependency>
      <groupId>com.google.guava</groupId>
      <artifactId>guava</artifactId>
      <version>31.1-jre</version>
    </dependency>

直接使用里面的 BloomFilter 工具

public class BloomFilterUtil {

    /**
     * 预期存储1000w数据
     */
    static final int expect = 10_000_000;
    /**
     * 误差率
     */
    static final double fpp = 0.0001;

    static Random random = new Random();

    public static BloomFilter<String> create() {
        return BloomFilter.create(Funnels.stringFunnel(Charset.defaultCharset()), expect, fpp);
    }

    public static void main(String[] args) {
        List<String> exist = new ArrayList<>();
        BloomFilter<String> stringBloomFilter = create();
        for (int i = 0; i < 10000000; i++) {
            String str = UUID.randomUUID().toString();
            stringBloomFilter.put(str);
            if (i < 1000000) {
                // 存储100w的数据
                exist.add(str);
            }
        }
        // 再造1000000w不存在的数据
        List<String> unExist = new ArrayList<>();
        for (int i = 0; i < 1000000; i++) {
            unExist.add(UUID.randomUUID().toString());
        }
        // 已存在的看看是不是全部命中了
        int existCount = 0;
        for (int i = 0; i < exist.size(); i++) {
            if (stringBloomFilter.mightContain(exist.get(i))) {
                existCount++;
            }
        }
        // 不存在的看看命中多少
        int unExistCount = 0;
        for (int i = 0; i < unExist.size(); i++) {
            if (stringBloomFilter.mightContain(unExist.get(i))) {
                unExistCount++;
            }
        }
        // 最终计算命中率和误判率
        NumberFormat pf = NumberFormat.getPercentInstance();
        pf.setMaximumFractionDigits(2);

        System.out.println("命中个数：" + existCount + "，误判个数：" + unExistCount);
        float r1 = (float) existCount / exist.size();
        float r2 = (float) unExistCount / unExist.size();
        System.out.println("命中率为：" + pf.format(r1) + "，误判率为：" + pf.format(r2));

        // 命中个数：1000000，误判个数：94
        // 命中率为：100%，误判率为：0.01%

    }
}
  • fpp : 期望误报率
  • expect：期望插入的数据

4. 源码

4.1 创建 BloomFilter

BloomFilter.create(Funnels.stringFunnel(Charset.defaultCharset()), expect, fpp);

上面就是创建布隆过滤器的方法，可以看到参数传入了Funnel、expectedInsertions、fpp，Funne 就是这个布隆过滤器是用来处理什么类型的，直接看 create 方法

@VisibleForTesting
static <T> BloomFilter<T> create(Funnel<? super T> funnel, long expectedInsertions, double fpp, BloomFilter.Strategy strategy) {
	// 参数检测，不为空
    Preconditions.checkNotNull(funnel);
    // 期望的插入数量必须要 >= 0
    Preconditions.checkArgument(expectedInsertions >= 0L, "Expected insertions (%s) must be >= 0", expectedInsertions);
    // 误差率需要在（0，0，1.0）之间
    Preconditions.checkArgument(fpp > 0.0D, "False positive probability (%s) must be > 0.0", fpp);
    Preconditions.checkArgument(fpp < 1.0D, "False positive probability (%s) must be < 1.0", fpp);
    // 策略接口，里面就是往布隆过滤器里面加入数据、判断是否存在等方法
    // 默认实现是 MURMUR128_MITZ_64
    Preconditions.checkNotNull(strategy);
    if (expectedInsertions == 0L) {
        expectedInsertions = 1L;
    }
	// 求出在当前误差率和数据量的情况下，需要多少的数位
    long numBits = optimalNumOfBits(expectedInsertions, fpp);
    // 需要 hash 方法的个数
    int numHashFunctions = optimalNumOfHashFunctions(expectedInsertions, numBits);

    try {
    	// 创建 BloomFilter 对象返回
        return new BloomFilter(new LockFreeBitArray(numBits), numHashFunctions, funnel, strategy);
    } catch (IllegalArgumentException var10) {
        throw new IllegalArgumentException((new StringBuilder(57)).append("Could not create BloomFilter of ").append(numBits).append(" bits").toString(), var10);
    }
}

可以看到里面的参数校验，期望插入的数据 >= 0，并且误差率范围需要在（0，1）之间，我们主要关注optimalNumOfBits和optimalNumOfHashFunctions方法

@VisibleForTesting
static long optimalNumOfBits(long n, double p) {
     // 如果概率是 0，就设置成 double 的最小值
     // 布隆过滤器是不可能没有误报的，只是概率多少的问题
     if (p == 0.0D) {
         p = 4.9E-324D;
     }
     // 下面这个公式就是第二节最后求出的 m 的值
     return (long)((double)(-n) * Math.log(p) / (Math.log(2.0D) * Math.log(2.0D)));
 }

@VisibleForTesting
static int optimalNumOfHashFunctions(long n, long m) {
	// 求出期望的 hash 函数个数
    return Math.max(1, (int)Math.round((double)m / (double)n * Math.log(2.0D)));
}

首先是 optimalNumOfBits 方法，这个方法中其实就是调用了 Math 方法去求需要多少位： m = − n ∗ l n p ( l n 2 ) 2 m=\frac{-n*lnp}{(ln2)^2} \newline\newline m=(ln2)2−n∗lnp​
再看 optimalNumOfHashFunctions 方法，这个方法也是调用了 Math 方法去求 hash 函数的个数： m n l n 2 \frac{m}{n}ln2 nm​ln2

在封装 numBits 的时候，使用了 LockFreeBitArray 来进行封装，核心的逻辑就是在里面处理的：

static final class LockFreeBitArray {
	...
}

4.2 LockFreeBitArray

这个类内部方法不多，对于位的处理就在里面，首先来看构造方法：

LockFreeBitArray(long bits) {
	// bits 位数要大于 0
    Preconditions.checkArgument(bits > 0L, "data length is zero!");
    // 创建一个原子 long 类型的数组
    // 一个 long 类型有
    this.data = new AtomicLongArray(Ints.checkedCast(LongMath.divide(bits, 64L, RoundingMode.CEILING)));
    // 位数计算
    this.bitCount = LongAddables.create();
}

下面再来看 set 方法，set 方法指定一个 bitIndex，把对应的 index 设置为 1

boolean set(long bitIndex) {
  // 如果该 index 已经设置为 1 了，返回 false
  if (get(bitIndex)) {
    return false;
  }
  // 当前 bitIndex 属于哪一个 long
  int longIndex = (int) (bitIndex >>> LONG_ADDRESSABLE_BITS);
  // 哪一位设置为 1
  long mask = 1L << bitIndex; // only cares about low 6 bits of bitIndex
	
  long oldValue;
  long newValue;
  do {
  	// 旧的值
    oldValue = data.get(longIndex);
    // 新的值
    newValue = oldValue | mask;
    // 如果相等，就不用设置了
    if (oldValue == newValue) {
      return false;
    }
    // CAS 设置
  } while (!data.compareAndSet(longIndex, oldValue, newValue));

  // 又设置了一位，bitCount++
  bitCount.increment();
  return true;
}

// 判断这个位是不是已经设置为 1 了
boolean get(long bitIndex) {
  // bitIndex >>> LONG_ADDRESSABLE_BITS 求出属于哪个下标
  // 1L << bitIndex 求出属于这个下标的哪一位
  return (data.get((int) (bitIndex >>> LONG_ADDRESSABLE_BITS)) & (1L << bitIndex)) != 0;
}

这个方法就是具体设置 bit 为 1 的方法，首先进来先通过 get 方法判断下这个位是不是已经设置为 1 了，如果已经设置了，就直接返回 false

  • bitIndex >>> LONG_ADDRESSABLE_BITS: 相当于 bitIndex / 64，求出当前的 index 属于哪一个 long，前面说过，LockFreeBitArray 里面使用 long 类型数组来管理每一个 bit，因为一个 long 类型 64 位，能代表 64 个 bit，所以需要先求出下标
  • 1L << bitIndex: 这里可能有点难理解，但是我给个例子你就明白了，1 << 64 = 1，1 << 65 = 2，1 << 128 = 1，这意味着 0~ 63 是一个循环，64 ~ 127 是一个循环，1L << bitIndex，实际上相当于 1 << (bitIndex % 64)，所以这里实际上就是求出来这是在第几位
  • 最终相 |，就能求出最新的值了
  • 举个例子，比如 longIndex = 129，那么 bitIndex >>> LONG_ADDRESSABLE_BITS = 2，1 << 129 = 2，所以我们要将下标 2 的 long 的第 2 位设置为 1

4.3 Strategy

interface Strategy extends java.io.Serializable {

  /**
   * Sets {@code numHashFunctions} bits of the given bit array, by hashing a user element.
   *
   * <p>Returns whether any bits changed as a result of this operation.
   */
  <T extends @Nullable Object> boolean put(
      @ParametricNullness T object,
      Funnel<? super T> funnel,
      int numHashFunctions,
      LockFreeBitArray bits);

  /**
   * Queries {@code numHashFunctions} bits of the given bit array, by hashing a user element;
   * returns {@code true} if and only if all selected bits are set.
   */
  <T extends @Nullable Object> boolean mightContain(
      @ParametricNullness T object,
      Funnel<? super T> funnel,
      int numHashFunctions,
      LockFreeBitArray bits);

  /**
   * Identifier used to encode this strategy, when marshalled as part of a BloomFilter. Only
   * values in the [-128, 127] range are valid for the compact serial form. Non-negative values
   * are reserved for enums defined in BloomFilterStrategies; negative values are reserved for any
   * custom, stateful strategy we may define (e.g. any kind of strategy that would depend on user
   * input).
   */
  int ordinal();
}

Strategy 就是具体的策略接口，里面提供了三个方法，ordinal 先不管，put 就是往 BloomFilter 里面去设置一条数据，mightContain 就是去判断 BloomFilter 里面有没有这条数据，具体实现类是 BloomFilterStrategies，是一个枚举类，提供了两种实现：MURMUR128_MITZ_32 和 MURMUR128_MITZ_64，下面就来看看这两种实现类，默认创建是使用 MURMUR128_MITZ_64

4.3.1 MURMUR128_MITZ_32

/**
 * funnel: 将 Object 转成 Hash 值
 * See "Less Hashing, Same Performance: Building a Better Bloom Filter" by Adam Kirsch and Michael
 * Mitzenmacher. The paper argues that this trick doesn't significantly deteriorate the
 * performance of a Bloom filter (yet only needs two 32bit hash functions).
 */
MURMUR128_MITZ_32() {
  @Override
  public <T extends @Nullable Object> boolean put(
      @ParametricNullness T object,
      Funnel<? super T> funnel,
      int numHashFunctions,
      LockFreeBitArray bits) {
    // 当前 bit 数组里面总共有多少个 bit，就是数组长度 * 64
    long bitSize = bits.bitSize();
    // 通过 MurmurHash3 算法求出 hash 值，非对称加密
    long hash64 = Hashing.murmur3_128().hashObject(object, funnel).asLong();
    // hash64 的低 32 位
    int hash1 = (int) hash64;
    // hash64 的高 32 位
    int hash2 = (int) (hash64 >>> 32);
	// 数组是否有变化
    boolean bitsChanged = false;
    // numHashFunctions 个 hash 值
    for (int i = 1; i <= numHashFunctions; i++) {
      // 通过 hash1 + (i * hash2) 计算出一个新的哈希值
      int combinedHash = hash1 + (i * hash2);
      // 如果 combinedHash 是负数，则取其按位取反（~combinedHash），确保 combinedHash 是正数
      if (combinedHash < 0) {
        combinedHash = ~combinedHash;
      }
      // 设置对应的 index = 1
      bitsChanged |= bits.set(combinedHash % bitSize);
    }
    // 是否有变化
    return bitsChanged;
  }
  
  @Override
  public <T extends @Nullable Object> boolean mightContain(
      @ParametricNullness T object,
      Funnel<? super T> funnel,
      int numHashFunctions,
      LockFreeBitArray bits) {
    // 位数组的大小
    long bitSize = bits.bitSize();
    // hash 值
    long hash64 = Hashing.murmur3_128().hashObject(object, funnel).asLong();
    // 低 32 位
    int hash1 = (int) hash64;
    // 高 32 位
    int hash2 = (int) (hash64 >>> 32);
	// numHashFunctions 个 hash 值
    for (int i = 1; i <= numHashFunctions; i++) {
      // 通过 hash1 和 hash2 求出的 hash 值
      int combinedHash = hash1 + (i * hash2);
      // 确保 hash 值是正数
      if (combinedHash < 0) {
        combinedHash = ~combinedHash;
      }
      // 如果不存在，返回false
      if (!bits.get(combinedHash % bitSize)) {
        return false;
      }
    }
    // 全部 hash 值都存在就返回 true
    return true;
  }
}

逻辑不复杂，就是通过 MurmurHash3 算法求出 hash 值，然后以低 32 位为 hash1，高 32 位为 hash2 来计算其他的 hash 值，至于为什么两个 hash 就能求出其他的 hash，注释已经说明了论文：《Less hashing, same performance: building a better bloom filter》使用了两个 32 位的哈希函数，而不是多个哈希函数来优化传统布隆过滤器通常需要多个哈希函数带来的性能损耗，有兴趣可以看看
求出 combinedHash 个 hash 值，依次判断是否都在 bit 数组中，如果都存在，就返回 true，否则 返回 false

4.3.2 MURMUR128_MITZ_64

/**
 * This strategy uses all 128 bits of {@link Hashing#murmur3_128} when hashing. It looks different
 * than the implementation in MURMUR128_MITZ_32 because we're avoiding the multiplication in the
 * loop and doing a (much simpler) += hash2. We're also changing the index to a positive number by
 * AND'ing with Long.MAX_VALUE instead of flipping the bits.
 */
MURMUR128_MITZ_64() {
  @Override
  public <T extends @Nullable Object> boolean put(
      @ParametricNullness T object,
      Funnel<? super T> funnel,
      int numHashFunctions,
      LockFreeBitArray bits) {
    // 位数组的大小
    long bitSize = bits.bitSize();
    // 利用了 hash 函数的全部 128 位，返回一个长度为 16 的 byte 数组
    byte[] bytes = Hashing.murmur3_128().hashObject(object, funnel).getBytesInternal();
    // 下标[0, 7]
    long hash1 = lowerEight(bytes);
    // 下标[8, 15]
    long hash2 = upperEight(bytes);
	// 数组是否有修改
    boolean bitsChanged = false;
    // hash1
    long combinedHash = hash1;
    for (int i = 0; i < numHashFunctions; i++) {
      // 设置对应位为 1
      bitsChanged |= bits.set((combinedHash & Long.MAX_VALUE) % bitSize);
      // 简单加法，相当于 hash1 + i * hash2，跟上面 MURMUR128_MITZ_32 一样的
      combinedHash += hash2;
    }
    // 数组是否有变化
    return bitsChanged;
  }

  @Override
  public <T extends @Nullable Object> boolean mightContain(
      @ParametricNullness T object,
      Funnel<? super T> funnel,
      int numHashFunctions,
      LockFreeBitArray bits) {
    // 位数组的大小
    long bitSize = bits.bitSize();
    // 利用了 hash 函数的全部 128 位，返回一个长度为 16 的 byte 数组
    byte[] bytes = Hashing.murmur3_128().hashObject(object, funnel).getBytesInternal();
    // 下标[0, 7]
    long hash1 = lowerEight(bytes);
    // 下标[8, 15]
    long hash2 = upperEight(bytes);
	// hash1
    long combinedHash = hash1;
    for (int i = 0; i < numHashFunctions; i++) {
      // 判断对应位是否为 1，如果不是，返回 false
      if (!bits.get((combinedHash & Long.MAX_VALUE) % bitSize)) {
        return false;
      }
      combinedHash += hash2;
    }
    return true;
  }

  private /* static */ long lowerEight(byte[] bytes) {
    return Longs.fromBytes(
        bytes[7], bytes[6], bytes[5], bytes[4], bytes[3], bytes[2], bytes[1], bytes[0]);
  }

  private /* static */ long upperEight(byte[] bytes) {
    return Longs.fromBytes(
        bytes[15], bytes[14], bytes[13], bytes[12], bytes[11], bytes[10], bytes[9], bytes[8]);
  }
};

MURMUR128_MITZ_64 和 MURMUR128_MITZ_32 有一点不一样

  • MURMUR128_MITZ_32 只是用了 64 位来计算 hash，MURMUR128_MITZ_64 使用所有 128 位哈希值，这个策略使用 MurmurHash3 128 位哈希函数的全部 128 位来生成哈希值，而不是只使用低 32 位。
  • 避免乘法运算：在循环中，这个策略避免了乘法运算，而是简单地将 hash2 加到 combinedHash 上
  • 使用 Long.MAX_VALUE 来确保正数索引：这个策略通过与 Long.MAX_VALUE 进行按位与操作，确保 combinedHash 是正数，而不是通过翻转位来实现

总的来说就是 hash 的计算位数不一样


5. 总结

布隆过滤器（Bloom Filter）是一种空间效率极高的概率型数据结构，用于判断一个元素是否存在于一个集合中。它的主要优点是占用空间小、查询速度快，但也有一定的误判率（即可能会把不在集合中的元素误判为存在），所以布隆过滤器特别适用于那些需要快速判断元素是否存在于集合中，并且可以容忍一定误判率的场景

  • 解决 Redis 缓存穿透问题
  • URL 去重
  • 黑名单过滤
  • 垃圾邮件过滤
  • …





如果错误，欢迎指出！！！

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
windows 无法运行powershell脚本 |.ps1 : 无法加载文件 | .ps1，因为在此系统上禁止运行脚本。
js之事件循环(event loop)
JS缓存三种方法
STLINK烧写器下载程序时，无法烧录并提示“USB communitate error”问题
生成式AI发展方向讨论
MySQL的update理解,批量更新问题: 同一张表中根据某个字段与另一个字段值,更新第三个字段
自学黑客，一般人我劝你还是算了吧
输入一行字符，分别统计出其中英文字母、空格、数字和其他字符的个数
Prolog语言及程序设计汇总
VirtualBox 下USB 设备加载的步骤及无法加载的解决办法
;