二分类的 DiceLoss 损失函数

二分类 Dice 系数计算

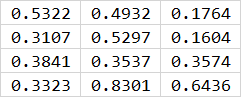
假设模型输出的预测值 preds 经过 sigmoid 后，得到 logits 如下所示

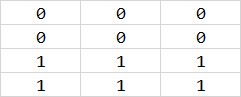
该 logits 对应的标签 label 如下所示，0 表示不属于某一类，1 表示属于某一类：

根据 DiceLoss 系数的定义有：
$$\begin{array}{rl}|X\cap Y|& =\left[\begin{array}{ccc}0.5322& 0.4932& 0.1764\\ 0.3107& 0.5297& 0.1604\\ 0.3841& 0.3537& 0.3574\\ 0.3323& 0.8301& 0.6436\end{array}\right]\star \left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]\\ & =\left[\begin{array}{ccc}0.0000& 0.0000& 0.0000\\ 0.0000& 0.0000& 0.0000\\ 0.3841& 0.3537& 0.3574\\ 0.3323& 0.8301& 0.6436\end{array}\right]\to 2.9012(求和)\end{array}$$

$$|X|=\left[\begin{array}{ccc}0.5322& 0.4932& 0.1764\\ 0.3107& 0.5297& 0.1604\\ 0.3841& 0.3537& 0.3574\\ 0.3323& 0.8301& 0.6436\end{array}\right]\to 5.1038$$

$$|Y|=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]\to 8$$

所以 Dice 系数为
$$D=\frac{2\ast |X\cap Y|+1}{|X|+|Y|+1}=\frac{2\ast 2.9012+1}{5.1038+8＋1}=0.5901$$

所以 Dice 损失 $L=1-D=0.4099$

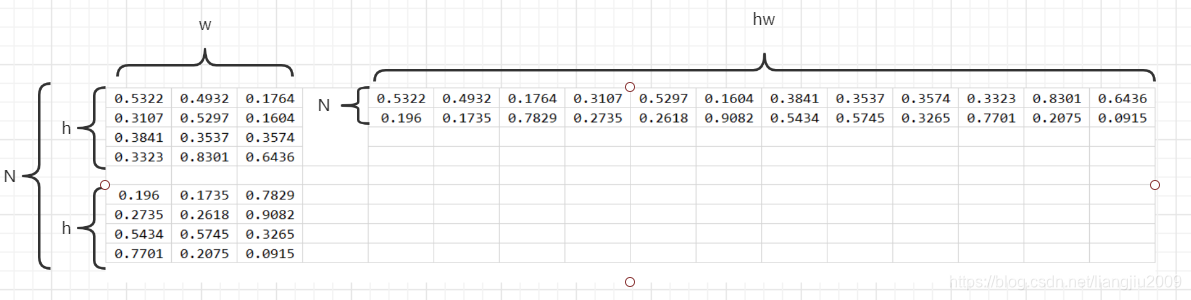
这是二分类一个批次只有一张图的情况，当一个批次有 $N$ 张图片时，可以将图片压缩为一维向量，如下所示：

对应的 label 也做相应的变换，最后一起计算 $N$ 张图片的 Dice 系数 和 Loss。

上面这个过程的 pytorch 代码实现如下所示;

import torch
import torch.nn as nn

class BinaryDiceLoss(nn.Model):
	def __init__(self):
		super(BinaryDiceLoss, self).__init__()
	
	def forward(self, input, targets):
		# 获取每个批次的大小 N
		N = targets.size()[0]
		# 平滑变量
		smooth = 1
		# 将宽高 reshape 到同一纬度
		input_flat = input.view(N, -1)
		targets_flat = targets.view(N, -1)
	
		# 计算交集
		intersection = input_flat * targets_flat 
		N_dice_eff = (2 * intersection.sum(1) + smooth) / (input_flat.sum(1) + targets_flat.sum(1) + smooth)
		# 计算一个批次中平均每张图的损失
		loss = 1 - dice_eff.sum() / N
		return loss

多分类 DiceLoss 损失函数

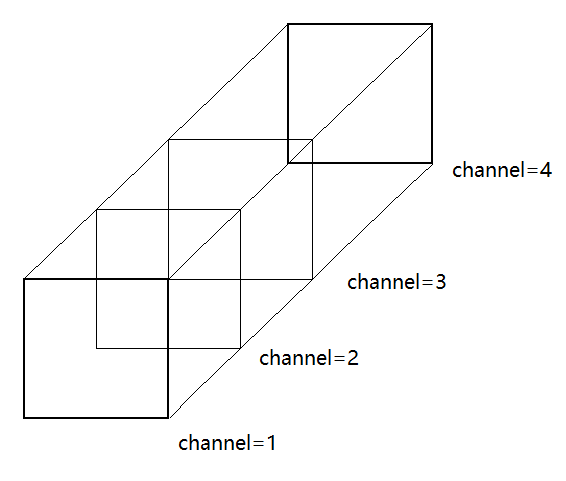
当有多个分类时，label 通过 one hot 转化为多个二分类，如下图所示：

每个channel 切面，可以看作是一个二分类问题，所以多分类 DiceLoss 损失函数，可以通过计算每个类别的二分类 DiceLoss 损失，最后再求均值得到。pytorch 代码如下所示：

import torch
import torch.nn as nn

class MultiClassDiceLoss(nn.Module):
	def __init__(self, weight=None, ignore_index=None, **kwargs):
		super(MultiClassDiceLoss, self).__init__()
		self.weight = weight
		self.ignore_index = ignore_index
		self.kwargs = kwargs
	
	def forward(self, input, target):
		"""
			input tesor of shape = (N, C, H, W)
			target tensor of shape = (N, H, W)
		"""
		# 先将 target 进行 one-hot 处理，转换为 (N, C, H, W)
		nclass = input.shape[1]
		target = one_hot(target.long(), nclass)

		assert input.shape == target.shape, "predict & target shape do not match"
		
		binaryDiceLoss = BinaryDiceLoss()
		total_loss = 0
		
		# 归一化输出
		logits = F.softmax(input, dim=1)
		C = target.shape[1]
		
		# 遍历 channel，得到每个类别的二分类 DiceLoss
		for i in range(C):
			dice_loss = binaryDiceLoss(logits[:, i], target[:, i])
			total_loss += dice_loss
		
		# 每个类别的平均 dice_loss
		return total_loss / C