目录

单链无头无循环链表的基本：

1：反转链表

2：移除链表元素（快慢指针）

3：合并两个有序链表（双指针）

4：环形链表|（快慢指针）

5:环形链表||（快慢指针+简单数学）

6：相交链表（双指针）

7:删除链表的倒数第N个节点（快慢指针）

8：奇偶链表

9：回文链表（快慢指针）

力扣的双指针模板：

单链无头无循环链表的基本：

（1）链表的结构体：

struct ListNode {

   int val;

   struct ListNode *next;

  };

（2）定义指针指向：

struct ListNode* n1=head

定义一个链表型的n1的指针指向头地址

（3）指向下一个地址

n1=n1->next;

(4)指向该地址所存储的值

 n1->val

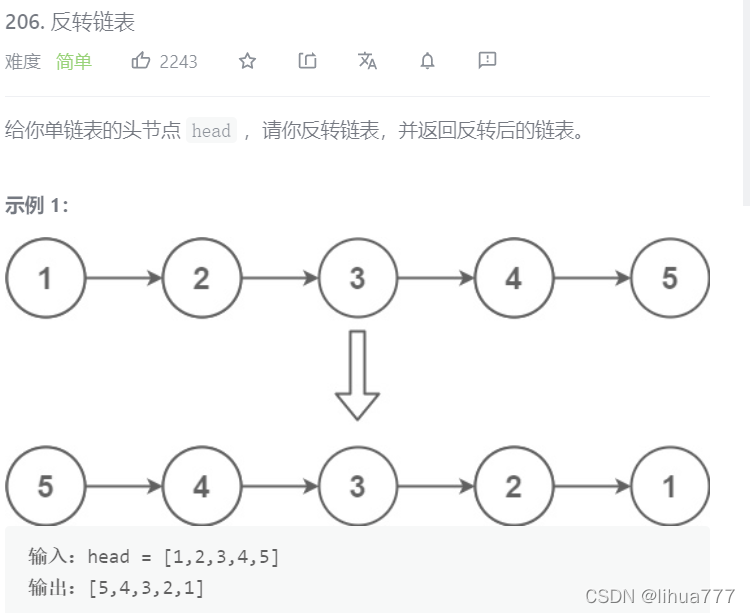
1：反转链表

思路解析：

定义三个结构体型的指针，*n1，*n2，*n3

（1）初始化：n1=NULL   n2=head    n3=head->next;

（2）本质是将n2->next=n1  由于n1始终在n2的左边，所以反转链表即将n2指向n1即可

（3）然后将n1=n2 n2=n3  n3=n3->next;  

意义是n1跑到n2的位置，n2跑到n3的位置，n3指向下一个地址

 结束条件：

画图解释：

 如图所示：当n2为最后一个节点时，是最后一个步骤

所以迭代条件是n2!=NULL

至于为什么是用三个指针，因为:n2->next=n1

会导致n2找到不到它在原链表的下一个节点，无法进行迭代

代码实现：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* reverseList(struct ListNode* head){
    if (head == NULL)
	{
		return NULL;
	}
	struct ListNode* n1 = NULL;
	struct ListNode* n2 = head;
	struct ListNode* n3 = n2->next;

	while (n2)
	{
		n2->next = n1;
		n1 = n2;
		n2 = n3;
		if (n3)
		{
			n3 = n3->next;
		}
	}
	return n1;
}

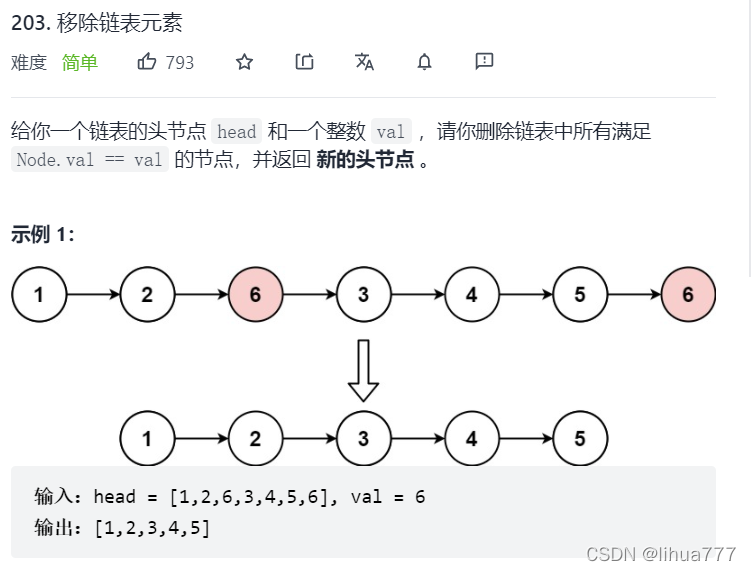
2：移除链表元素（快慢指针）

 思路解析：

（1）定义结构体型的两个快慢指针（跟班指针）*cur 和 *pre

初始化为*cur=head *pre=head 都指向头节点

（2）如果cur->val!=target，那么pre=cur (就让pre跟上cur)

         如果cur->val==target，那么就让pre->next=cur->next;(pre指向cur的下一个节点)

跳过了cur所处的目标值的位置，相当于pre指向的节点所存的地址修改为后两个节点的地址

        同时每次都让cur=cur->next; 让cur每次都指向下一个地址

（3）迭代条件：当cur！=NULL

 代码实现：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* removeElements(struct ListNode* head, int val){
    while (head != NULL && head->val == val) {
		head = head->next;//防止链表都是同一个元素的情况
	}

	struct ListNode* cur = head;  //  当前节点
	struct ListNode* pre = head;  //  保存待删除节点的前一节点
	while (cur != NULL) {
		if (cur->val == val) {
			pre->next = cur->next;
		}
		else {
			pre = cur;
		}
		cur = cur->next;
	}

	return head;
}

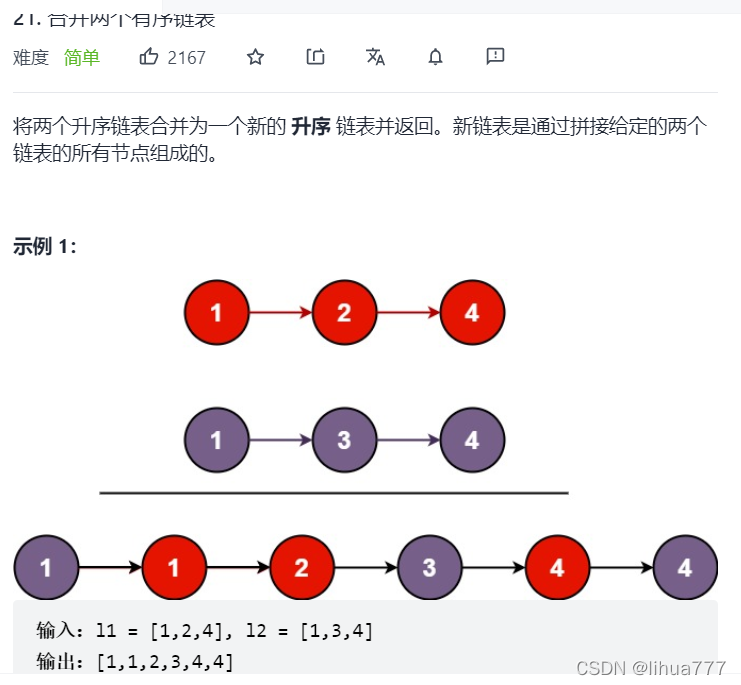
3：合并两个有序链表（双指针）

 思路解析：

分析：这道题与合并数组几乎相同

因为这两个链表都是有序的，又让我们合并为有序的，我们只需搞初始化两个指针分别指向链表的head，然后将head->val进行比较，小的就尾插新链表，尾插好后，将原来指向较小数的指针右移，再进行比较，重复此过程即可

注意：我们这里需要加判断：如果有其中一个链表已经空了（元素都被选完了），我们直接让另外一个链表尾插入新链表即可

返回时：返回的时head->next而不是head，因为此时的头节点并没有存储数据

 代码实现：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2){
    if(l1==NULL) return l2;
    if(l2==NULL) return l1;
    struct ListNode *head=NULL,*tail=NULL;
    head=tail=(struct ListNode*)malloc(sizeof(struct ListNode));
    while(l1!=NULL && l2!=NULL)
    {
        if(l1->val < l2->val)
        {
            tail->next=l1;
            l1=l1->next;
        }
        else
        {
            tail->next=l2;
            l2=l2->next;
        }
        tail=tail->next;
    }
    if(l1!=NULL) tail->next=l1;
    if(l2!=NULL) tail->next=l2;
    head=head->next;//易错！！！！！
    
    return head;
}

易错：因为head和tail初始化时时同一个空间，而后tail作为尾，尾插数据，head作为头不变，head本身不存储任何数据，所以其相当于一开始的tail,那么让head=head->next即tail尾插的第一个数据的节点，即head指向第一个节点的地址

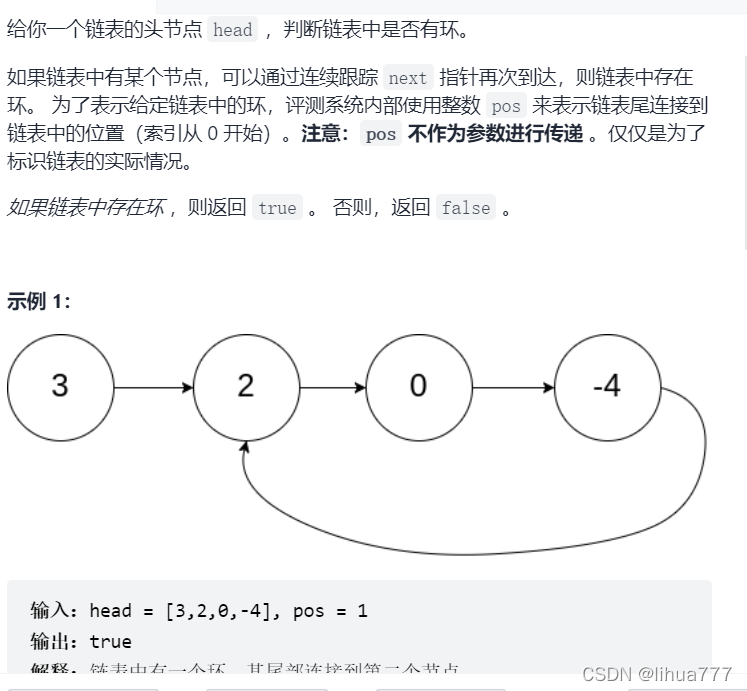
4：环形链表|（快慢指针）

 思路解析：

有环->重复（指的是地址）

无环->不重复（指的是地址）

因为地址是独特的，而值重复出现是正常的

我们选择用快慢指针来做，并进行追逐

初始化 *slow=head *fast=head;

迭代过程： slow=slow->next;  fast=fast->next->next; 

slow指针一次走一步，fast指针一次走两步

迭代条件：fast!=NULL && fast->next!=NULL (因为fast是一次走两步)

核心：如果slow=fast那么就 break return true;证明有环

反之return false;

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) {
    struct ListNode *slow=head,*fast=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)  return true;
    }
    return false;
}

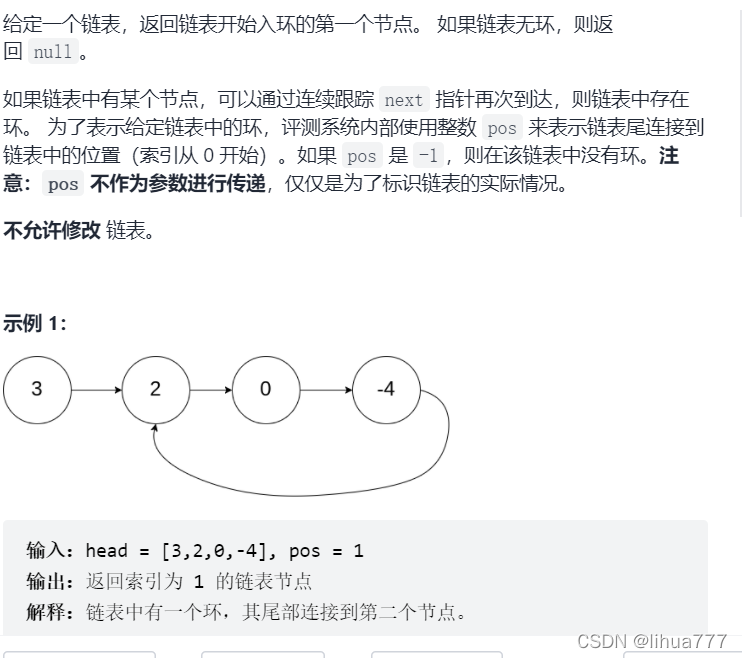
5:环形链表||（快慢指针+简单数学）

 思路解析：

上题让我们证明是否有环，此题让我们寻找环的入口，同样的快慢指针，但是需要数学证明

力扣官方数学证明：力扣

结论:上题快慢指针的相遇点和指向头节点的指针同时出发，它们相遇的地方即是环的入口点

代码实现：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode*slow=head,*fast=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;

        if(slow==fast)
        {
            struct ListNode*meet=slow;//相遇点指针
            while(head!=meet)
            {
                head=head->next;//头指针
                meet=meet->next;
            }
            return meet;//出循环证明head==meet，该地址就是环入口
        }
    }
    return NULL;
}

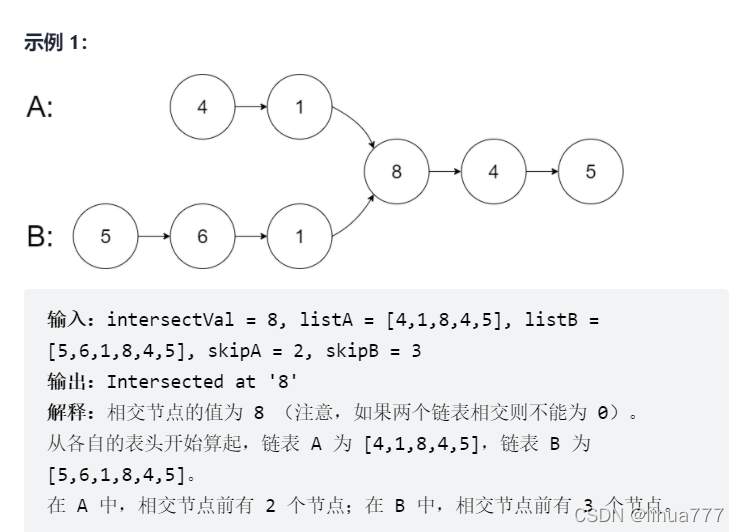
6：相交链表（双指针）

 思路解析：

初始化*pA=headA  *pB=headB

只要当pA==pB时，就能够说明两个链表相交

难点在于：由于这两个链表的长度不一定相等，所以一般的遍历是找不到答案的

会有错过的情况发生，那么怎么解决呢？

非常巧妙：

如果我走到了尾（NULL），还没有找到你，那么我就从你的头再遍历一次

这样只用遍历最多两次即可找到：因为链表长度的差值因为两次的重新开始而被抹平

 代码实现：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    if (headA == NULL || headB == NULL) {
        return NULL;
    }
    struct ListNode *pA = headA, *pB = headB;
    while (pA != pB) {
        pA = pA == NULL ? headB : pA->next;
        pB = pB == NULL ? headA : pB->next;
    }
    return pA;
}

可以自己用两个手指进行模拟，非常巧妙^ ^

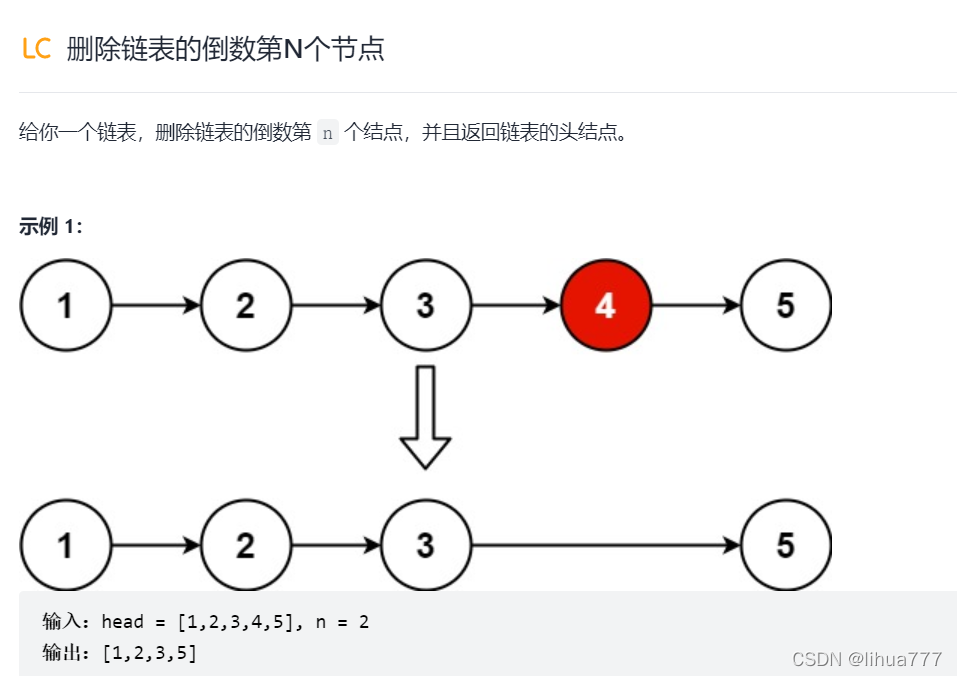
7:删除链表的倒数第N个节点（快慢指针）

 思路解析：

我们这里先给出删除链表的正数第N个节点的代码：

struct ListNode* cur = head;  //  当前节点
	struct ListNode* pre = head;  //  保存待删除节点的前一节点
    int i=0;
	while (cur != NULL ) {
		if (i==n-1) {
			pre->next = cur->next;
		}
		else {
			pre = cur;
		}
		cur = cur->next;
        i++;
	}

思路解析：

用i记录走的步数，如果步数==目标节点数-1 我们即将prev指向cur的下一个位置即可

 本题的笨方法：

遍历一遍链表，获取链表的总节点数n;

if(n-N==i) prev->next=cur->next;

else prev=cur;

cur=cur->next;

i++;

本题的巧方法：

先让for(int i=0;i<N;i++) fast=fast->next; fast目前处于正数第N个位置

遍历整个链表（分两种情况）

（1）链表只有一个节点时，删除倒数第一个，即此时fast经过上面的for已经为空了

所以返回时，将head=head->next即返回空链表

（2）正常情况（不止有一个节点），fast指向最后一个节点，slow指针的的下一个节点变为它的下两个节点的地址

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* removeNthFromEnd(struct ListNode* head, int n){
    struct ListNode* slow = head;
	struct ListNode* fast = head;

	for (int i = 0; i < n; i++) fast = fast->next;
	while (fast != NULL && fast->next != NULL)
	{
		slow = slow->next;
		fast = fast->next;
	}
	if (fast == NULL) return head->next;
	else slow->next = (slow->next)->next;

	return head;
}

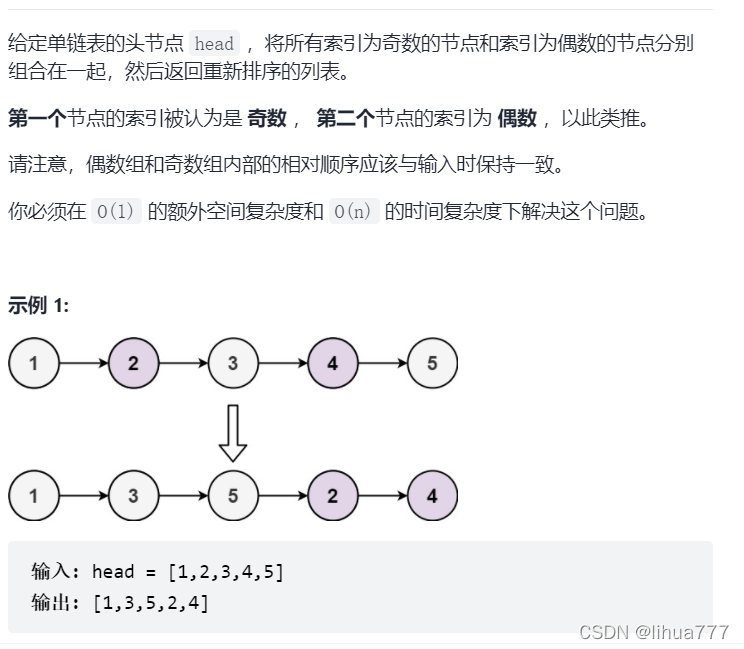
8：奇偶链表

 思路解析：

奇数的下一个是偶数

偶数的下一个是奇数

将奇数与奇数链接，将偶数与偶数链接，将奇数的最后一个与第一个偶数链接

由于迭代过程中数据会被破坏，所以我们需要一个偶数头来存储偶数头的地址

迭代过程：

odd=even->next;

even=odd->next;

odd=odd->next;

even=even->next;

迭代条件：even!=NULL && even->next!=NULL (考虑只有1个或2个节点的特殊情况)

跳出循环后：奇数和偶数指针一定都指向了各自的最后一个节点，那么我们需要将奇数的最后一个节点存偶数的第一个节点的地址，以此达到链接的效果

 代码实现：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */

struct ListNode* oddEvenList(struct ListNode* head){
    if (head == NULL) return head;
	struct ListNode* evenHead = head->next;
	struct ListNode* odd = head;
	struct ListNode* even = evenHead;//初始化
	while (even != NULL && even->next != NULL)//迭代条件
	{
		odd->next = even->next;//迭代过程
		odd = odd->next;
		even->next = odd->next;
		even = even->next;
	}
	odd->next = evenHead;//链接
	return head;
}

9：回文链表（快慢指针）

 思路解析：

方法一：

可将链表遍历，存入数组中，在数组中判断是否回文

bool isPalindrome(struct ListNode* head) {
    int vals[50001], vals_num = 0;
    while (head != NULL) {
        vals[vals_num++] = head->val;
        head = head->next;
    }
    for (int i = 0, j = vals_num - 1; i < j; ++i, --j) {
        if (vals[i] != vals[j]) {
            return false;
        }
    }
    return true;
}

 方法二：

（1）用快慢指针，慢指针走一步，快指针走两步，以此来找到中间节点（分奇偶情况）

（2）将后半部分链表进行反转

（3）两个链表此时正序，依次判断值->是否相等

（4）还原链表

 有点点小难……………………

struct ListNode* reverseList(struct ListNode* head) {//反转链表
    struct ListNode* prev = NULL;
    struct ListNode* curr = head;
    while (curr != NULL) {
        struct ListNode* nextTemp = curr->next;//类似于swap函数
        curr->next = prev;
        prev = curr;
        curr = nextTemp;//加了一个类似与i++的迭代，使得链表向前遍历
    }
    return prev;
}

struct ListNode* endOfFirstHalf(struct ListNode* head) {//快慢指针找中间结点
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while (fast->next != NULL && fast->next->next != NULL) {//奇偶情况都要考虑
        fast = fast->next->next;
        slow = slow->next;
    }
    return slow;
}

bool isPalindrome(struct ListNode* head) {
    if (head == NULL) {
        return true;
    }

    // 找到前半部分链表的尾节点并反转后半部分链表
    struct ListNode* firstHalfEnd = endOfFirstHalf(head);//前半部分
    struct ListNode* secondHalfStart = reverseList(firstHalfEnd->next);//后半部分=后半部分的反转-注意传的是中间的下一个结点的地址

    // 判断是否回文
    struct ListNode* p1 = head;
    struct ListNode* p2 = secondHalfStart;
    bool result = true;
    while (result && p2 != NULL) {//两个链表正序判断
        if (p1->val != p2->val) {//正序判断值是否相等->回文
            result = false;
        }
        p1 = p1->next;//迭代
        p2 = p2->next;
    }

    // 还原链表并返回结果
    firstHalfEnd->next = reverseList(secondHalfStart);
    return result;
}

此题用递归更为简单，以后看看悟了的话就出递归版的= =

力扣的双指针模板：

// Initialize slow & fast pointers
ListNode* slow = head;
ListNode* fast = head;
/**
 * Change this condition to fit specific problem.
 * Attention: remember to avoid null-pointer error
 **/
while (slow && fast && fast->next) {
    slow = slow->next;          // move slow pointer one step each time
    fast = fast->next->next;    // move fast pointer two steps each time
    if (slow == fast) {         // change this condition to fit specific problem
        return true;
    }
}
return false;   // change return value to fit specific problem

主要注意整个while的条件判断，因为要考虑到只有一个结点的情况