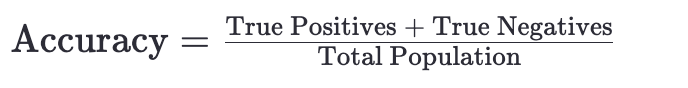机器学习案例：幸福感指数预测

案例简介

本项目通过幸福感预测这一经典社会科学课题，使用问卷调查所得的公开数据，包括个体变量（性别、年龄、地域、职业、健康、婚姻与政治面貌等等）、家庭变量（父母、配偶、子女、家庭资本等等）、社会态度（公平、信用、公共服务等等）等134 个维度的信息来预测其对幸福感的影响。幸福感happiness 分为1 = 非常不幸福; 2 = 比较不幸福; 3 = 说不上幸福不幸福; 4 = 比较幸福; 5 = 非常幸福; 一共 5 个等级，需要根据其他特征来预测样本的happiness属于哪个分类。本案例来自阿里云天池大赛。

数据集介绍

变量个数较多，部分变量间关系复杂，数据分为完整版和精简版两类。可从精简版入手熟悉赛题后，使用完整版挖掘更多信息。

complete文件为变量完整版数据。
abbr文件为变量精简版数据。
index文件中包含每个变量对应的问卷题目，以及变量取值的含义。
survey文件是数据源的原版问卷，作为补充以方便理解问题背景。

数据来源：国家官方的《中国综合社会调查（CGSS）》文件

回归与分类

首先需要搞明白这是一个分类问题，还是一个回归问题，
幸福感happiness 分为1 = 非常不幸福; 2 = 比较不幸福; 3 = 说不上幸福不幸福; 4 = 比较幸福; 5 = 非常幸福; 一共 5 个等级，

有人说，这是一个分类问题，因为happiness的取值个数是有限个，具有离散的特性。

也有人说，则是一个回归问题，因为分类问题的标签的离散值之间是独立的，没有强弱或者程度的联系，这个案例中，幸福感从等级 1非常不幸福，到等级 5非常幸福，标签值之间，带有明显的程度特点，并不是独立的无关系的。

阿里元天池大赛，官方给出的评价指标是均方误差MSE，均方误差MSE是衡量回归模型的重要指标，明显官方把这个问题定性为一个回归问题了。

我认为，虽然幸福感被分为了5个等级（1到5），但这个问题更适合作为一个分类问题来处理，而不是回归问题。原因如下：

离散的类别：幸福感的五个等级是离散的、有序的类别，而不是连续的数值。每个等级代表一种明确的状态，而不是一个可以任意取值的连续变量。
有序性：虽然这些类别是有序的（即1 < 2 < 3 < 4 < 5），但这并不意味着它们之间的差距是等距的。例如，从“非常不幸福”到“比较不幸福”的变化可能与从“比较幸福”到“非常幸福”的变化在心理上的影响是不同的。
分类模型的优势：使用分类模型（如逻辑回归、随机森林、XGBoost等）可以直接输出属于每个类别的概率，这有助于更好地理解和解释模型的预测结果。

作为一个多分类问题来处理，选择分类算法和评估指标（如准确率、F1分数、混淆矩阵等）。

幸福感预测

导入模块

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from lightgbm import LGBMClassifier,log_evaluation
from sklearn.metrics import mean_squared_error, r2_score,accuracy_score,classification_report,confusion_matrix,f1_score
from sklearn.model_selection import StratifiedKFold,GridSearchCV,RandomizedSearchCV
from xgboost import XGBClassifier
from sklearn.preprocessing import LabelEncoder
from imblearn.over_sampling import SMOTE

读取精简版数据集

精简版数据集happiness_train_abbr.csv，总共8000 条数据，有 41 个特征列，1 个标签列。


#用来正常显示中文标签
plt.rcParams['font.sans-serif']=['Arial Unicode MS']
data = pd.read_csv(filepath_or_buffer="./幸福感预测数据集/happiness_train_abbr.csv")
data.info()
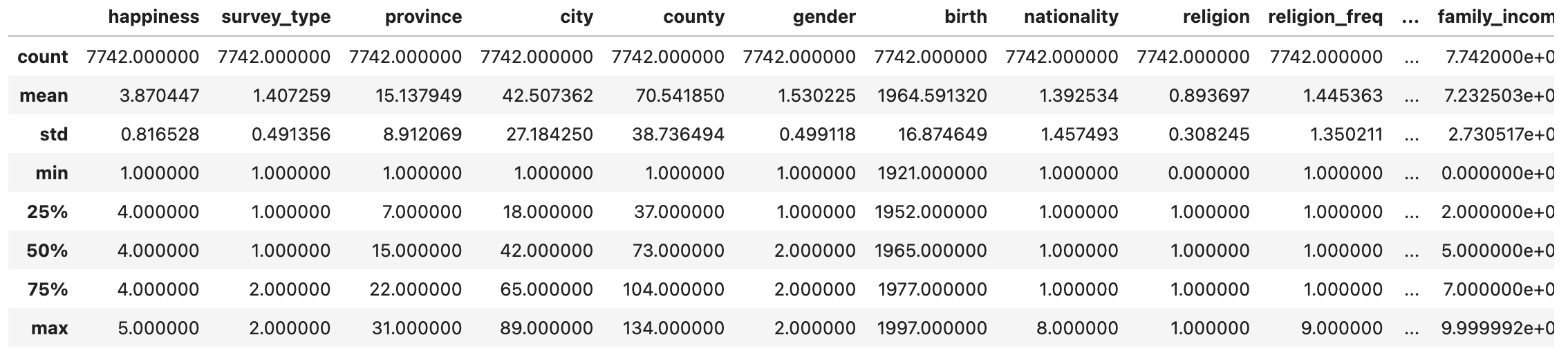
# 查看特征的数据分布
data.describe()

数据清洗

# 判断是否有重复值
data.duplicated(subset=['id']).sum() # 输出0，没有重复的

# 删除无用的列表:问卷时间
data.drop(columns=['survey_time'],inplace=True)
data.drop(columns=['id'],inplace=True)
data.shape # 输出(8000, 40)

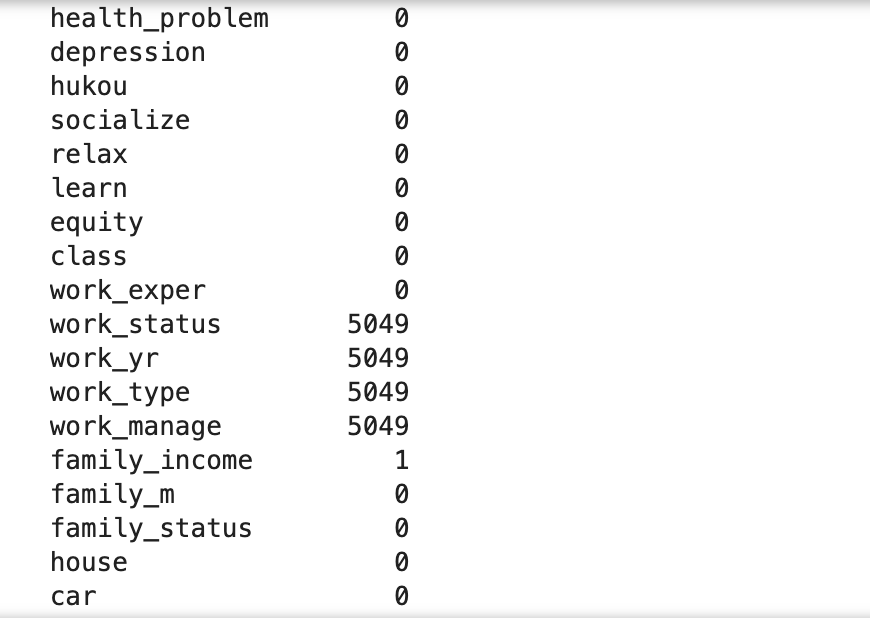
# 统计缺失值
data.isna().sum()

缺失值统计输出：
在这里插入图片描述

# 异常值处理
# 删除happiness异常数据，-8不知道是什么标签
condition = data['happiness'] > -8
# 使用条件筛选删除异常值
data = data[condition]

condition = data['nationality'] > -8
data = data[condition]

#对‘宗教’处理
data.loc[data['religion']<0,'religion'] = 1 #1为不信仰宗教
data.loc[data['religion_freq']<0,'religion_freq'] = 1 #1为从来没有参加过

#对‘教育程度’处理
data.loc[data['edu']<0,'edu'] = 4 #初中

#对‘个人收入’处理
data.loc[data['income']<0,'income'] = 0 #认为无收入

#对‘政治面貌’处理
data.loc[data['political']<0,'political'] = 1 #认为是群众

#对‘健康’处理
data.loc[data['health']<0,'health'] = 4 #认为是比较健康
data.loc[data['health_problem']<0,'health_problem'] = 4

#对‘沮丧’处理
data.loc[data['depression']<0,'depression'] = 4 #一般人都是很少吧

data.loc[data['socialize']<0,'socialize'] = 2 #很少


condition = data['relax'] > -8
data = data[condition]

condition = data['learn'] > -8
data = data[condition]

condition = data['equity'] > -8
data = data[condition]

#对‘社会等级’处理
data.loc[data['class']<0,'class'] = 5

condition = data['work_status'] != -8
data = data[condition]
#工作状态空值的情况，给一个默认值，0：未知
data.loc[data['work_status']<0,'work_status'] = 0
data['work_status'] = data['work_status'].fillna(0)

data.loc[data['work_type']<0,'work_type'] = 0
data['work_type'] = data['work_type'].fillna(0)

#工作年数 空值的情况，给一个默认值0
data['work_yr'].fillna(0, inplace=True)
condition = data['work_yr'] >= 0
data = data[condition]

#工作的性质 空值的情况，给一个默认值0:未知
data.loc[data['work_yr']<0,'work_yr'] = 0

#工作的管理活动情况，空值的情况，给一个默认值0:未知
data['work_manage'] = data['work_manage'].fillna(0)
data.loc[data['work_manage']<0,'work_manage'] = 0

#对家庭情况处理
family_income_mean = data['family_income'].mean()
data.loc[data['family_income']<0,'family_income'] = family_income_mean
data['family_income'] = data['family_income'].fillna(family_income_mean)


data.loc[data['family_m']<0,'family_m'] = 2

data.loc[data['family_status']<0,'family_status'] = 3

data.loc[data['house']<0,'house'] = 1

#data.loc[data['car']<0,'car'] = 0

#和同龄人相比社会经济地位
data.loc[data['status_peer']<0,'status_peer'] = 2

#和3年前比社会经济地位
data.loc[data['status_3_before']<0,'status_3_before'] = 2

#对‘观点’处理
data.loc[data['view']<0,'view'] = 4

#对期望年收入处理
data.loc[data['inc_ability']<=0,'inc_ability']= 2

# 查看列的取值是否正常
# 查看 列中每种枚举值的个数
sort_value = np.sort(data['inc_ability'].unique())
print(f"排序之后的枚举值：{sort_value}")
value_counts = (data['inc_ability'] < 0).sum()
print(f"异常值个数：{value_counts}")
print(f"空值值个数：{data.isna().sum()['inc_ability']}")

# 初步查看一下，数据情况
data.describe()

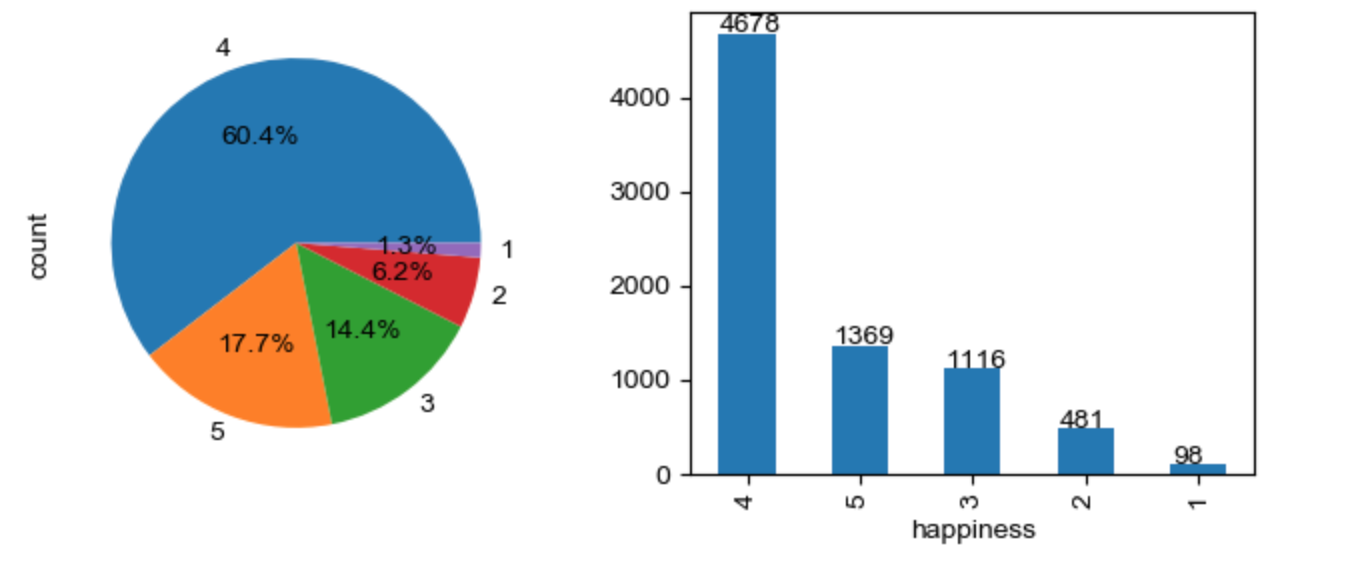
在这里插入图片描述

数据清理完成之后，查看幸福等级happiness 标签数据分布情况

# happiness 分为 5 个等级
# 1 = 非常不幸福; 2 = 比较不幸福; 3 = 说不上幸福不幸福; 4 = 比较幸福; 5 = 非常幸福; 

# 创建一个新的图形窗口，设置其大小为宽度 8 英寸、高度 3 英寸。
plt.figure(figsize=(8, 3))
# 在当前图形中创建一个 1 行 2 列的子图布局，并激活第一个子图（即左侧的子图）。
plt.subplot(1, 2, 1)
# data['happiness'].value_counts():计算 "happiness" 列中每个值出现的次数。
# 返回一个 Series，索引是 "happiness" 的不同取值，值是这些取值对应的频数。
# .plot(kind='pie', autopct='%1.1f%%'): 使用计算出的频数绘制饼图。
# autopct='%1.1f%%' 参数用于在饼图的各部分显示百分比，格式化为小数点后一位的百分数形式。
data['happiness'].value_counts().plot(kind='pie', autopct='%1.1f%%')
# 激活第二个子图（即右侧的子图）。
plt.subplot(1, 2, 2)
# 同样地计算 "happiness" 列中每个值的频数，并使用这些频数绘制柱状图。
happiness_ax = data['happiness'].value_counts().plot(kind='bar')
# 在柱状图上显示具体的数字
# 循环遍历每个柱形 happiness_ax.patches 包含了所有柱形对象。
for p in happiness_ax.patches:
	# 对每个柱形添加注释，显示该柱形的高度（即频数）。
	# p.get_height() 获取柱形的高度，p.get_x() 获取柱形左边缘的 x 坐标。
	# 乘以一个小于 1 的系数（如 1.005）是为了稍微偏移文本位置，避免文本直接覆盖在柱形之上。
    happiness_ax.annotate(str(p.get_height()), (p.get_x() * 1.005, p.get_height() * 1.005))
# 显示图形
plt.show()

在这里插入图片描述

目标变量（幸福指数）类别分布极不均衡，幸福指数为 1，占比最少，才 1.3%，为 2占比 6.2%，为 3占比 14.4%，为 4占比最多 60.4%，为 5占比17.7%，

数据预处理

删除相关性比较低的列

# 选择标签列
column_name = 'happiness'
# 计算相关矩阵
corr_matrix = data.corr()
# 提取感兴趣列与其他列的相关性
correlations_with_column = corr_matrix[column_name]
# 按照相关性值从高到低排序
correlations_with_column_sorted = correlations_with_column.sort_values(ascending=False)
print("按照相关性值从高到低排序:")
print(correlations_with_column_sorted)

# 相关性靠前的特征
top_feature = []
# 删除的列
del_feature = []
# 设置相关性阈值
threshold = 0

for col_name in correlations_with_column_sorted.index:
    #print(f"列名：{col_name},相关性：{correlations_with_column_sorted[col_name]}")
    if correlations_with_column_sorted[col_name] > threshold:
        top_feature.append(col_name)
    #删除不相关的特征
    if correlations_with_column_sorted[col_name] <= threshold:
        print("删除不相关的特征:{}".format(col_name))
        del_feature.append(col_name)
        data.drop(columns=[col_name],inplace=True)

print("剩余特征列:{}".format(top_feature))

剩余特征列:[‘happiness’, ‘depression’, ‘family_status’, ‘class’, ‘equity’, ‘health’, ‘health_problem’, ‘relax’, ‘view’, ‘learn’, ‘edu’, ‘house’, ‘political’, ‘weight_jin’, ‘socialize’, ‘hukou’, ‘family_m’, ‘family_income’, ‘floor_area’, ‘height_cm’, ‘income’, ‘gender’, ‘work_type’, ‘religion_freq’, ‘work_yr’, ‘work_manage’, ‘work_status’, ‘work_exper’]

数据拆分

from sklearn.model_selection import train_test_split

y = data["happiness"].to_numpy()
X = data.drop(columns=["happiness"]).to_numpy()

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
X_train.shape, y_train.shape,X_test.shape, y_test.shape

标准化处理

# 从训练集中抽取预处理参数 mu 和 sigma
mu = X_train.mean(axis=0)
sigma = X_train.std(axis=0)
# 执行标准化操作
X_train = (X_train - mu) / sigma
X_test = (X_test - mu) / sigma

模型训练

使用XGBoost的分类器（XGBClassifier）结合随机搜索（RandomizedSearchCV）来优化模型参数，并评估其在测试集上的性能。

#使用 XGBClassifier
# random_state=42 设置随机种子为42以确保结果的可重复性，
# verbosity = 0关闭冗长的日志输出。
xgb4 = XGBClassifier(random_state=42,verbosity = 0)
# 使用 LabelEncoder 将训练集和测试集的目标变量转换为从0开始的连续整数，
# 因为XGBoost需要数值型标签而非字符串或类别型标签。
label_encoder4 = LabelEncoder()
y_train_encoded4 = label_encoder4.fit_transform(y_train)
y_test_encoded4 = label_encoder4.transform(y_test)

# 设置参数分布
# 定义一组要调优的超参数及其可能的值。
# n_estimators 表示要构建的树的数量（即 boosting 迭代次数）
# max_depth 树的最大深度，限制了树的生长程度。
# learning_rate 收缩步长，每次更新后对权重进行调整的比例。
# subsample 训练每棵树时使用的样本比例。
# colsample_bytree 训练每棵树时使用的特征比例
# n_estimators 和 max_depth：这两个参数共同决定了模型的复杂度。增加树的数量或树的深度可以使模型更加复杂，从而能够捕捉到数据中更多的细节，但同时也增加了过拟合的风险。
# subsample 和 colsample_bytree：这两种采样方法（行采样和列采样）都是为了增加模型的随机性，从而提高其泛化能力和稳定性，同时降低过拟合的可能性。
param_dist4 = {
    'n_estimators': [100, 200, 300, 400],
    'max_depth': [3, 5, 7, 9, 20],
    'learning_rate': [0.01, 0.05, 0.1, 0.2],
    'subsample': [0.6, 0.8, 1.0],
    'colsample_bytree': [0.6,0.8,1.0]
}

# 使用RandomizedSearchCV进行超参数调优，通过随机搜索在指定的参数空间中寻找最佳参数组合。
# n_iter=10表示将随机抽取10种不同的参数组合进行尝试，cv=3表示采用3折交叉验证。
random_search4 = RandomizedSearchCV(estimator=xgb4, param_distributions=param_dist4,
                                   n_iter=10, scoring='accuracy', cv=3, verbose=1, 
                                   random_state=42, n_jobs=-1)

# 在训练集上拟合RandomizedSearchCV
random_search4.fit(X_train, y_train_encoded4)

# 打印找到的最佳参数，并使用这些参数对应的模型作为最终模型。
print("Best parameters found: ", random_search4.best_params_)
# 使用找到的最佳参数重新训练模型
best_model4 = random_search4.best_estimator_

# 在测试集上做出预测
y_pred4 = best_model4.predict(X_test)

# 计算准确率
accuracy4 = accuracy_score(y_test_encoded4, y_pred4)
print(f"Accuracy on test set: {accuracy4:.4f}")

# 打印分类报告
print(classification_report(y_test_encoded4, y_pred4))

预测结果：

Fitting 3 folds for each of 10 candidates, totalling 30 fits
Best parameters found:  {'subsample': 0.6, 'n_estimators': 100, 'max_depth': 7, 'learning_rate': 0.01, 'colsample_bytree': 1.0}
Accuracy on test set: 0.6085
              precision    recall  f1-score   support

           0       0.17      0.05      0.08        20
           1       0.28      0.11      0.16        96
           2       0.24      0.05      0.09       223
           3       0.64      0.95      0.76       935
           4       0.54      0.12      0.20       274

    accuracy                           0.61      1548
   macro avg       0.37      0.26      0.26      1548
weighted avg       0.53      0.61      0.52      1548

从结果上看，1548个测试样本集，准确率才 60%，准确率不高。绘制混淆矩阵，看看预计结果

# 将 y_pred4 和 y_test_encoded4 转换为 NumPy 数组
y_pred_discrete_confusion = np.array([val for val in y_pred4])
y_test_confusion = np.array([val for val in y_test_encoded4])
# 计算混淆矩阵。该函数接受真实标签和预测标签作为输入，
# 并返回一个二维数组，其中每个元素表示实际类别与预测类别之间的匹配情况
cm = confusion_matrix(y_test_confusion, y_pred_discrete_confusion)
# 创建一个 DataFrame 来存储混淆矩阵
# 1 = 非常不幸福; 2 = 比较不幸福; 3 = 说不上幸福不幸福; 4 = 比较幸福; 5 = 非常幸福; 
class_names = ['非常不幸福', '比较不幸福', '说不上幸福不幸福','比较幸福','非常幸福']
# 将混淆矩阵转换为 Pandas DataFrame 格式，行和列都对应于 class_names 中定义的类别名称。
# 这样做的好处是可以更方便地进行数据处理和可视化。
df_cm = pd.DataFrame(cm, index=class_names, columns=class_names)

# 使用 seaborn 绘制混淆矩阵
# 设置绘图窗口的大小，宽度为 7 英寸，高度为 5 英寸。
plt.figure(figsize=(7, 5))
# annot=True 表示在热图的每个单元格中显示数值。
# 设置颜色映射方案，"YlGnBu" 是一种渐变色系，从黄色到绿色再到蓝色。
# fmt='g' 控制单元格内文本的格式，'g' 表示通用格式（自动选择最合适的数字格式）。
sns.heatmap(df_cm, annot=True, cmap="YlGnBu", fmt='g')
plt.xlabel("Predicted")
plt.ylabel("Actual")
plt.title("Confusion Matrix")
plt.show()

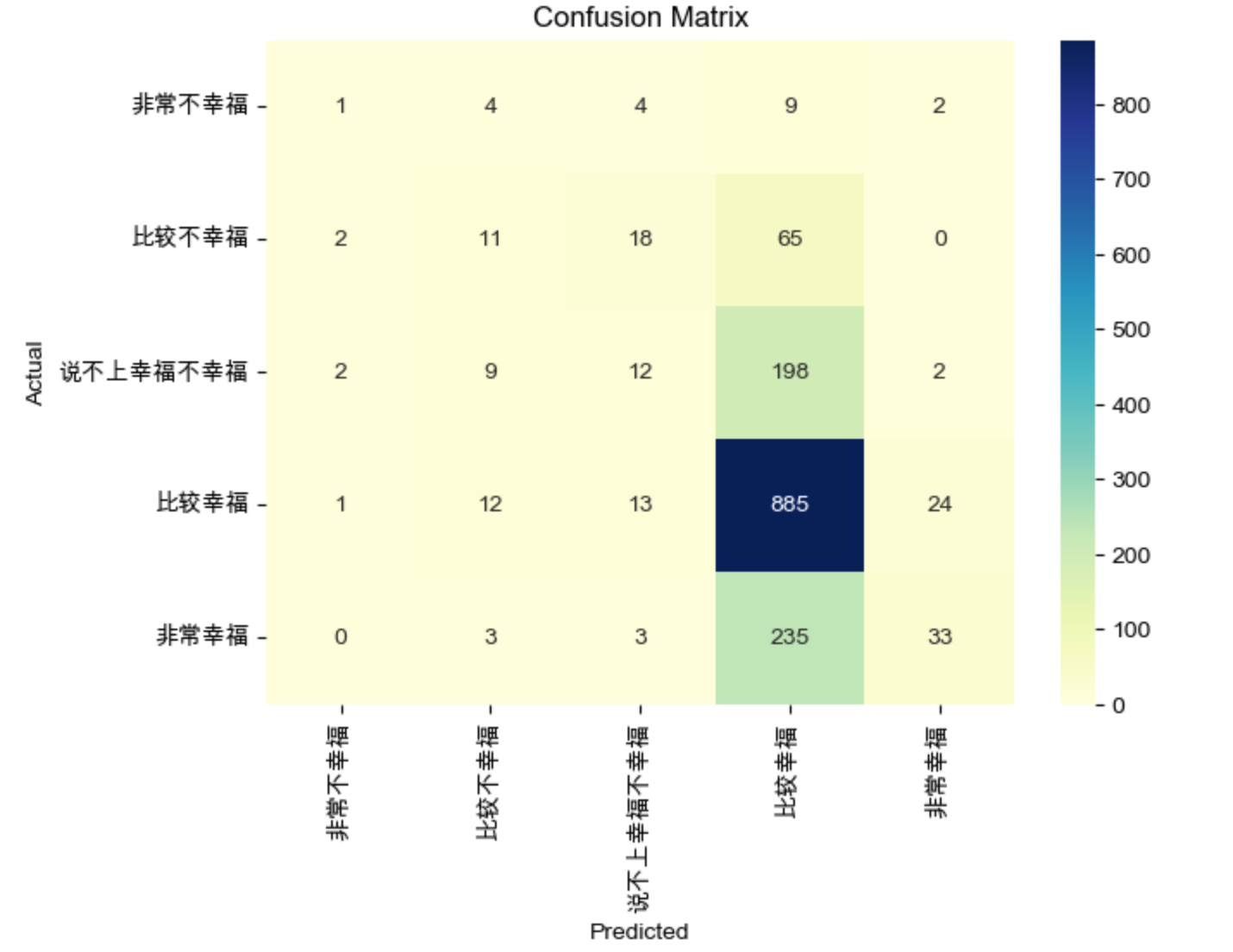
在这里插入图片描述

比较理想的情况是，混淆矩阵在对角线上，颜色最深，从上面这个图上看得出，只有比较幸福这个分类预测稍微好一点，其他分类都不理想，

导致这样的结果，可能是目标变量（幸福指数）类别分布极不均衡，可能会导致模型偏向于预测多数类。可以尝试过采样少数类、欠采样多数类或使用 SMOTE 等技术来平衡数据集。

模型优化

接下来使用优化策略

数据重采样：即过采样少数类，来优化模型训练，使用SMOTE通过生成合成样本来扩大少数类，通过增加少数类样本的数量来平衡数据集。
调整类权重：为不同的类别指定不同的权重。例如，在 XGBClassifier 中，你可以设置 scale_pos_weight 参数来平衡正负样本的比例。

SMOTE（合成少数类过采样技术）是一种处理不平衡数据集的技术，特别适用于分类问题中少数类样本数量远少于多数类样本的情况。SMOTE 的基本思想是通过生成少数类的新样本来增加其在数据集中的比例，从而帮助模型更好地学习到少数类的特征。

SMOTE 工作原理

选择样本：对于每一个少数类的样本 (x)，SMOTE 算法会找到其 k 个最近邻（通常使用欧氏距离）。(k) 是一个预先设定的参数，默认值通常是 5。
合成新样本：从这 (k) 个最近邻中随机选择一个样本 (x_nn)。然后，在 (x) 和 (x_nn) 之间生成一个新的样本。这个新样本的位置是在 (x) 到 (x_nn) 连线上的某一点，具体位置由一个介于 0 和 1 之间的随机数决定。数学上，新的样本可以通过以下公式计算得到：

在这里插入图片描述

其中，λ 是一个随机数，范围为 [0, 1]。

重复上述步骤：根据需要增加的少数类样本数量，重复上述过程，直到达到期望的平衡比例。

使用 SMOTE 进行过采样处理不平衡数据，然后利用 XGBoost 的 XGBClassifier 结合随机搜索 (RandomizedSearchCV) 来优化模型参数，并评估模型在测试集上的性能。

# 过采样处理不平衡数据,使用 XGBClassifier
# SMOTE：通过合成少数类样本来平衡数据集。
# 这里使用 SMOTE 对原始特征 X 和目标变量 y 进行过采样处理，生成新的平衡数据集 X_resampled6 和 y_resampled6。
smote6 = SMOTE(random_state=42)
X_resampled6, y_resampled6 = smote6.fit_resample(X, y)

# 将过采样后的数据划分为训练集和测试集，其中测试集占 20%。
X_train6, X_test6, y_train6, y_test6 = train_test_split(X_resampled6, y_resampled6, test_size=0.2, random_state=42)

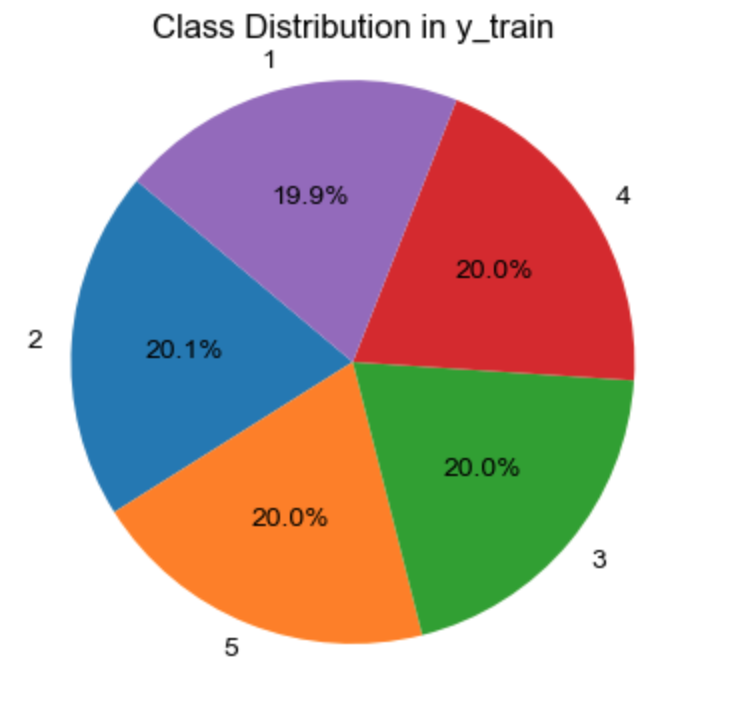
# 计算每个类别的频数
class_counts6 = Counter(y_train6)

# 获取类别名称和对应的频数
labels6 = class_counts6.keys()
sizes6 = class_counts6.values()

# 创建饼图
plt.figure(figsize=(5, 3))
plt.pie(sizes6, labels=labels6, autopct='%1.1f%%', startangle=140)
plt.axis('equal')  # 等轴比例，保证饼图是圆的
plt.title('Class Distribution in y_train')

# 显示图形
plt.show()

经过过采样处理之后，每个标签分类的占比，大致相当。
在这里插入图片描述

# 使用 LabelEncoder 将目标变量转换为从 0 开始的连续整数
label_encoder6 = LabelEncoder()
y_train_encoded6 = label_encoder6.fit_transform(y_train6)
y_test_encoded6 = label_encoder6.transform(y_test6)

# scale_pos_weight：用于调整正负样本的权重比例。这里计算的是类别 4（比较幸福）与其他类别的比例。
# scale_pos_weight 在处理二分类问题的时候比较有用，在此处，样本已经按照过采样处理之后，标签比较均衡，此处作用不明显，可以不使用
# 这个参数有助于处理类别不平衡的问题。
# y_train_encoded6.shape[0] 训练集中所有样本的总数。
# (y_train_encoded6 == 4).sum():计算训练集中标签为 4 的样本数量
# 减去 (y_train_encoded6 == 4).sum() 后，得到的是不属于类别 4 的所有其他类别的样本总数。
# / 计算非类别 4 样本与类别 4 样本之间的比例
xgb6 = XGBClassifier(scale_pos_weight=(y_train_encoded6.shape[0] - (y_train_encoded6 == 4).sum()) / (y_train_encoded6 == 4).sum(), 
                    random_state=42 ,verbosity = 0)

# 设置参数分布
param_dist6 = {
    'n_estimators': [100, 200, 300, 400],
    'max_depth': [3, 5, 7, 9, 20, 30],
    'learning_rate': [0.01, 0.05, 0.1, 0.2],
    'subsample': [0.6, 0.8, 1.0],
    'colsample_bytree': [0.6,0.8,1.0]
}

# 初始化RandomizedSearchCV
# 超参数调优，尝试不同的参数组合以找到最佳参数。
random_search6 = RandomizedSearchCV(estimator=xgb6, param_distributions=param_dist6,
                                   n_iter=10, scoring='accuracy', cv=3, verbose=1, 
                                   random_state=42, n_jobs=-1)

# 在训练集上拟合RandomizedSearchCV
random_search6.fit(X_train6, y_train_encoded6)

# 输出最佳参数组合
print("Best parameters found: ", random_search6.best_params_)
# 使用找到的最佳参数重新训练模型
best_model6 = random_search6.best_estimator_

# 在测试集上做出预测
y_pred6 = best_model6.predict(X_test6)

# 计算准确率
accuracy6 = accuracy_score(y_test_encoded6, y_pred6)
print(f"Accuracy on test set: {accuracy6:.4f}")

# 计算 F1 分数
f1_5 = f1_score(y_test_encoded6, y_pred6, average='weighted')
print(f"F1 Score: {f1_5}")

# 提供精确率、召回率和 F1 分数等详细的分类性能指标。
print(classification_report(y_test_encoded6, y_pred6))

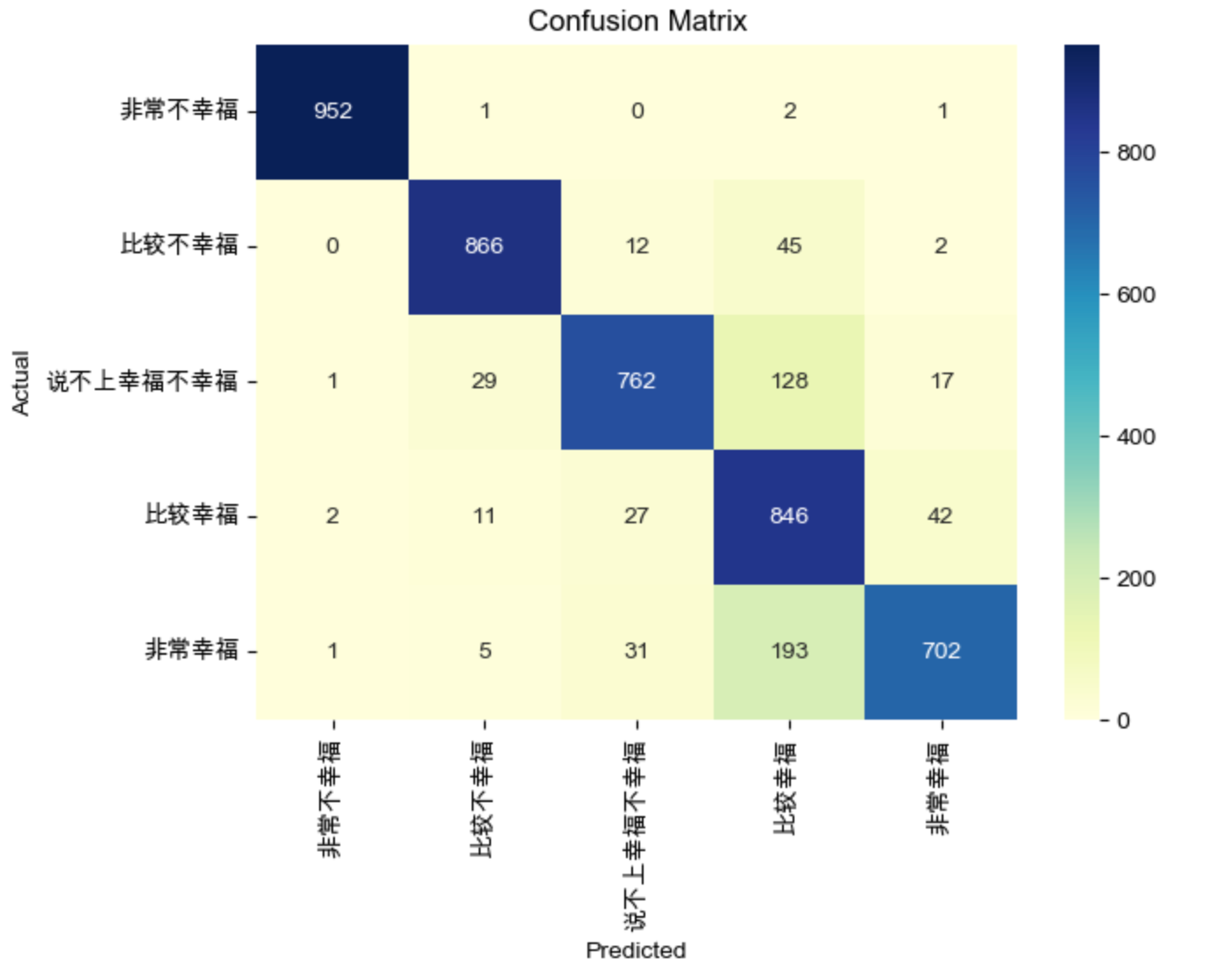
从下面的输出结果来看，准确提升到 88%

Fitting 3 folds for each of 10 candidates, totalling 30 fits
Best parameters found:  {'subsample': 0.6, 'n_estimators': 300, 'max_depth': 20, 'learning_rate': 0.1, 'colsample_bytree': 0.6}
Accuracy on test set: 0.8824
F1 Score: 0.8548157365581298
              precision    recall  f1-score   support

           0       1.00      1.00      1.00       956
           1       0.95      0.94      0.94       925
           2       0.92      0.81      0.86       937
           3       0.70      0.91      0.79       928
           4       0.92      0.75      0.83       932

    accuracy                           0.88      4678
   macro avg       0.90      0.88      0.88      4678
weighted avg       0.90      0.88      0.88      4678

重新绘制混淆矩阵

# 计算混淆矩阵
y_pred_discrete_confusion = np.array([val for val in y_pred6])
y_test_confusion = np.array([val for val in y_test_encoded6])
cm = confusion_matrix(y_test_confusion, y_pred_discrete_confusion)
# 创建一个 DataFrame 来存储混淆矩阵
# 1 = 非常不幸福; 2 = 比较不幸福; 3 = 说不上幸福不幸福; 4 = 比较幸福; 5 = 非常幸福; 
class_names = ['非常不幸福', '比较不幸福', '说不上幸福不幸福','比较幸福','非常幸福']
df_cm = pd.DataFrame(cm, index=class_names, columns=class_names)

# 使用 seaborn 绘制混淆矩阵
plt.figure(figsize=(7, 5))
sns.heatmap(df_cm, annot=True, cmap="YlGnBu", fmt='g')
plt.xlabel("Predicted")
plt.ylabel("Actual")
plt.title("Confusion Matrix")
plt.show()

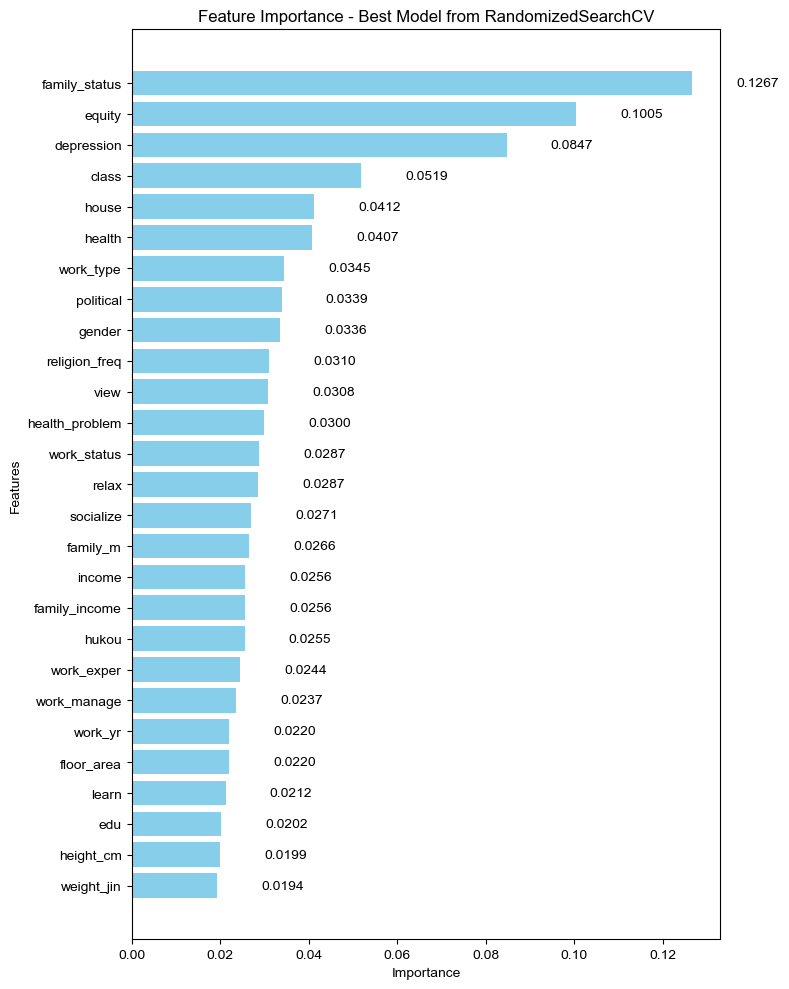
在这里插入图片描述

重要特征输出

# 获取特征名称
feature_names6 = data.drop(columns=["happiness"]).columns.tolist()

# 获取特征重要性
feature_importance6 = best_model6.feature_importances_

# 将特征名和对应的特征重要性组合起来，并按重要性降序排序
sorted_idx6 = np.argsort(feature_importance6)[::-1]
sorted_feature_names6 = np.array(feature_names6)[sorted_idx6]
sorted_importances6 = feature_importance6[sorted_idx6]

# 设置绘图大小
plt.figure(figsize=(8, 10)) # 调整图形大小以适应垂直布局

# 创建水平条形图
# 注意：这里不需要额外调整顺序，因为我们已经按重要性降序排列了
plt.barh(range(len(sorted_importances6)), sorted_importances6, align='center', color='skyblue')
plt.yticks(range(len(sorted_importances6)), sorted_feature_names6)

# 添加标题和标签
plt.title("Feature Importance - Best Model from RandomizedSearchCV")
plt.xlabel("Importance") # X轴标签变更为"重要性"
plt.ylabel("Features")   # Y轴标签变更为"特征"

# 显示数值
for i, v in enumerate(sorted_importances6):
    plt.text(v + 0.01, i, f"{v:.4f}", color='black', va='center')

# 反转Y轴，使最重要特征位于顶部
plt.gca().invert_yaxis()

# 显示图形
plt.tight_layout()  # 自动调整子图参数,使之填充整个图像区域
plt.show()

在这里插入图片描述
根据特征的重要性排序，排在前 3，分别是

family_status：您家的家庭经济状况在所在地属于哪一档
equity：总的来说，您认为当今社会公不公平
depression：以及在过去的四周中您感到心情抑郁或沮丧的频繁程度

针对这三个关键因素对幸福指数影响的解释，纯属于个人看法。

1. 您家的家庭经济状况在所在地属于哪一档

基本需求满足：家庭经济状况直接影响到个体及其家庭成员的基本生活需求是否得到满足，包括食物、住房、医疗保健等。当这些基础需求被充分满足时，个人更有可能体验到较高的幸福感。
心理安全感：经济稳定能提供一种心理上的安全感和对未来规划的信心，减少焦虑和不确定性带来的负面情绪。
生活质量：更高的经济水平通常意味着更好的教育机会、休闲活动参与度以及社交圈扩展的可能性，这些都是提升幸福感的重要因素。

2. 总的来说，您认为当今社会公不公平

社会正义感知：人们对社会公平性的看法深刻影响着他们对自己地位的认知及与他人关系的感受。在一个被认为公正的社会里，人们更容易感受到尊重和平等对待，从而促进积极的情感体验。
信任和社会凝聚力：如果大多数人相信社会制度是公平的，则社会内部的信任度会增加，社区间的合作和支持也会增强，这有助于构建和谐的人际关系网络，进而提高整体幸福感。
心理健康：长期处于不公平感强烈的环境中可能导致压力增大、情绪低落甚至抑郁等问题，反之则有利于保持良好的心理健康状态。

3. 在过去的四周中您感到心情抑郁或沮丧的频繁程度

直接关联：抑郁或沮丧情绪本身就是衡量个人心理健康状况的关键指标之一，而心理健康状况又直接关系到一个人的整体幸福感。
情感健康：持续的情绪低落不仅会影响日常生活质量，还可能损害人际关系和个人成就，进一步降低幸福感。
预警信号：频繁出现抑郁或沮丧情绪可能是其他潜在问题（如工作压力、家庭矛盾等）的表现形式，及时识别并解决这些问题对于维护高水平的幸福感至关重要。

这三个因素从物质保障、社会环境和个人心理健康三个层面共同作用于个体的幸福感受。它们分别代表了人类追求幸福生活的不同维度——物质基础、社会环境以及精神健康，因此在预测幸福指数时显得尤为重要。

幸福感预测数据集下载

打印在报告里support、accuracy 、macro avg、weighted avg 代表什么意思？

在分类报告中，accuracy、macro avg（宏平均）、和 weighted avg（加权平均）是评估分类模型性能的关键指标。

1. Accuracy（准确率）

定义：准确率是指所有预测正确的样本数（无论是哪个类别）占总样本数的比例。
公式：
适用场景：当你的数据集中的类别分布相对均衡时，准确率是一个很好的整体性能度量。然而，在类别极度不平衡的数据集中，高准确率可能具有误导性，因为它可能会被多数类的正确预测所主导。

2. Macro Avg（宏平均）

定义：宏平均是对每个类别的性能指标（如精确率、召回率、F1分数）分别计算后取平均值，不考虑类别的样本数量。
计算方法：
- 对于每个类别，单独计算其精确率、召回率和F1分数。
- 然后对这些值求平均，得到宏平均精确率、宏平均召回率和宏平均F1分数。
优点：给每个类别相同的权重，适合类别不平衡的情况，因为它不会偏向于大类。
缺点：如果某个小类的样本非常少，其指标波动会对宏平均产生较大影响。

3. Weighted Avg（加权平均）

定义：加权平均是根据每个类别实际出现的频率（即样本数量），对其性能指标进行加权平均。
计算方法：
- 首先，为每个类别计算其精确率、召回率和F1分数。
- 然后，按照每个类别在数据集中出现的次数作为权重，对这些值进行加权平均。
优点：考虑到类别大小差异，对于类别不平衡问题提供了一个更平衡的视角。
缺点：可能会受到多数类的影响，导致少数类的表现被掩盖。

示例解释

假设你有一个三类分类问题，且各类别标签分别为0、1、2，而测试集中的真实标签与预测标签如下：

              precision    recall  f1-score   support

           0       0.50      0.67      0.57         3
           1       0.00      0.00      0.00         1
           2       1.00      1.00      1.00         1

    accuracy                           0.60         5
   macro avg       0.50      0.56      0.52         5
weighted avg       0.70      0.60      0.64         5

Accuracy：0.60 表示在这5个测试样本中，有3个被正确分类。
Macro avg：这里，精确率是 (0.50 + 0.00 + 1.00) / 3 = 0.50；召回率是 (0.67 + 0.00 + 1.00) / 3 ≈ 0.56；F1分数是 (0.57 + 0.00 + 1.00) / 3 ≈ 0.52。注意，每个类别的贡献是相等的，不论它们的实际样本数量如何。
Weighted avg：精确率是 (0.503 + 0.001 + 1.001) / 5 = 0.70；召回率是 (0.673 + 0.001 + 1.001) / 5 = 0.60；F1分数是 (0.573 + 0.001 + 1.00*1) / 5 ≈ 0.64。这里的权重基于每个类别的支持度（即样本数量）。

通过比较这三个指标，可以全面了解模型在不同类别上的表现以及整体性能。特别是当处理不平衡数据集时，关注宏平均和加权平均能帮助识别模型是否对某些特定类别表现不佳。