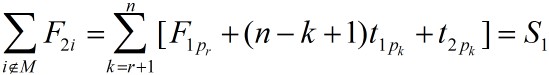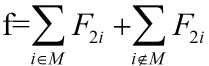问题描述

     给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理，然后由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。

     批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。

      例：设n=3，考虑以下实例：

     这3个作业的6种可能的调度方案是1,2,3；1,3,2；2,1,3；2,3,1；3,1,2；3,2,1；它们所相应的完成时间和分别是19，18，20，21，19，19。易见，最佳调度方案是1,3,2，其完成时间和为18。

     限界函数

     批处理作业调度问题要从n个作业的所有排列中找出具有最小完成时间和的作业调度，所以如图，批处理作业调度问题的解空间是一颗排列树。     

     在作业调度问相应的排列空间树中，每一个节点E都对应于一个已安排的作业集。以该节点为根的子树中所含叶节点的完成时间和可表示为：

     设|M|=r，且L是以节点E为根的子树中的叶节点，相应的作业调度为{pk,k=1,2,……n}，其中pk是第k个安排的作业。如果从节点E到叶节点L的路上，每一个作业pk在机器1上完成处理后都能立即在机器2上开始处理，即从pr+1开始，机器1没有空闲时间，则对于该叶节点L有：

注：(n-k+1)t1pk,因为是完成时间和，所以，后续的(n-k+1)个