基于函数逼近的同轨策略预测
我们前面已经完成了基于表格的学习任务,基于表格的就是每个s是独立学习的,基本上不考虑泛化的能力,但是也对于每个任务状态学习的非常好。考虑到状态空间越来越大,我们必须考虑到函数逼近的情况。
1. 概述
在实际问题中,状态空间往往很大或连 续,无法使用表格式方法存储每个状态的价值。例如我们的围棋(Go),1919,每个格子有三种状态,黑白空,状态的数量需要3^(1919),这个是很离谱的情况。
但是如果我们假设不同的状态之间有泛化的功能,我们可以学习到一些共同的函数和特征,往后面的几章都涉及到了很多的线性代数的运算,需要一定的数学的知识,如果大家的数学的功底不好的,可以去学习一下线性代数的基本内容。
2. 函数逼近的价值预测问题
整体来说,我们的学习的方法还是不变,我们依然是通过向一个目标值靠近的方式来进行学习,但是不同的是,我们是要对一个函数的权值进行学习,而不是一个个的特定的状态进行学习,换句话来说,一旦你学习了将会改变的不只是你当前的函数的价值函数,也会改变到其他的S状态的价值函数的评估
2.1 基本框架
函数逼近器接受状态s作为输入,输出对该状态值的估计v̂(s,w),其中w是可调整的权重向量。
目标是找到最优的权重w,使得估计值尽可能接近真实值。
2.2 训练数据
- 输入:状态s
- 目标:真实的状态值v_π(s)
- 实际使用时,我们用回报Gt作为v_π(s)的无偏估计
3. 随机梯度下降(SGD)方法
我们首先评估下一下,预测的目标是
V
E
ˉ
(
w
)
=
∑
s
μ
(
s
)
∗
[
V
π
(
s
)
−
V
(
S
,
w
)
]
2
\bar{VE}(w) = \sum_s\mu(s)*[V_\pi(s) - V(S,w)]^2
VEˉ(w)=∑sμ(s)∗[Vπ(s)−V(S,w)]2,
这个公式很容易理解,最小化带分布的所有的s的方差的值就是我们最靠近当前的价值函数的真实值的一个函数实现。
有一个很重要的概念后面会用到,我们这里的
μ
s
\mu_s
μs是s的真实的分布,本质上是s的状态被选择的概率,无论是开始的概率,还是在中间的任何状态s`切换到当前的s的概率之和,所以这个概率是一个稳态的概率,所以假设一个转移函数矩阵P,表示的是从任何的状态s切换到s’概率,那么矩阵
μ
=
P
μ
\mu=P\mu
μ=Pμ,这个很好理解,因为是稳定的状态,所以从当前的状态的进行转移以后得概率应该和当前没有发生转移的概率的是一致的,
3.1 均方误差目标
MSE(w) = u(s)E_π[(v_π(S) - v̂(S,w))²]
3.2 梯度下降更新规则
梯度下降的内容实际上是梯度VE的对于权值w的导数得来的,一定要注意的是,后面的那个部分是价值函数对于权值w的偏导数
避免有很多概念不明白的人看的很懵,我举个例子,假如价值函数的真实的表达是value = 2 * x_1 + 3* x_2,那么v对于x1,x2的偏导数分别是2,3,这也是后文说的,对于线性的情况,的偏导数就是X本身
w
t
+
1
=
w
t
+
α
[
v
π
(
S
t
)
−
v
^
(
S
t
,
w
t
)
]
∇
v
^
(
S
t
,
w
t
)
w_{t+1} = w_t + α[v_π(S_t) - v̂(S_t,w_t)]∇v̂(S_t,w_t)
wt+1=wt+α[vπ(St)−v^(St,wt)]∇v^(St,wt)
其中:
- α是步长参数
- ∇v̂(S_t,w_t)是v̂对w的梯度
注意,我们说这个是VE的对于w的偏导数,但是如果你仔细观察这里有一个书上没有提到的地方,就是原本的式子里面是有u的分布的,但是w是没有考虑这个u的分布的情况。
我看到比较好的解释是,这是一个隐性的分布,因为采集的比例本来就决定了更新的频率,换句话说,u变成了这个状态出现的概率,当然也变成了被更新的频率,我觉得说得通
SGD的通用的算法的表达是,对比上面的就知道,我们使用了真实的回报的来代替了真实的价值函数,因为真实的回报是真实的价值函数的无偏估计,也就是我们前面的所谓的蒙特卡洛算法的G_t的值
w
t
+
1
=
w
t
+
α
[
U
t
−
v
^
(
S
t
,
w
t
)
]
∇
v
^
(
S
t
,
w
t
)
w_{t+1} = w_t + α[U_t - v̂(S_t,w_t)]∇v̂(S_t,w_t)
wt+1=wt+α[Ut−v^(St,wt)]∇v^(St,wt)
4. 半梯度TD(0)方法
看了我们前面章节的内容的就知道,一开始都是蒙特卡洛的算法,然后就是TD(0)的算法,然后就是TD(n)的算法,然后就是更加复杂的期望,或者树的算法,对于函数逼近的情况也是一样,SGD的算法需要等到真实的价值函数才能进行学习,显然我们希望能学习到更快的学习函数,那就是TD(0)的算法
4.1 算法原理
TD(0)使用TD目标替代真实值:
w
t
+
1
=
w
t
+
α
[
R
t
+
1
+
γ
v
^
(
S
t
+
1
,
w
t
)
−
v
^
(
S
t
,
w
t
)
]
∇
v
^
(
S
t
,
w
t
)
w_{t+1} = w_t + α[R_{t+1} + γv̂(S_{t+1},w_t) - v̂(S_t,w_t)]∇v̂(S_t,w_t)
wt+1=wt+α[Rt+1+γv^(St+1,wt)−v^(St,wt)]∇v^(St,wt)
有一个很重要的问题就是为什么这里的叫做半梯度
4.2 为什么叫"半梯度"
这里最重要的原因就是式子里面的
γ
\gamma
γ的那一部分的值,
v
^
(
s
t
+
1
)
v̂(s_{t+1})
v^(st+1)显然也是一个需要使用权值w来进行计算的式子,那么VE的导数应该包含这一部分的对于w的偏导才对,但是显然这样就会变的非常的复杂,所以我们的半梯度就是忽略了t+1时刻的s的value函数的对于w的导数的情况
总结就是:
- 传统TD目标包含了对下一状态的估计值
- 但在更新时我们忽略了这部分的梯度
- 这种简化使算法更稳定
4.3 完整算法
输入:策略π要评估
参数:步长α
对每个回合:
初始化S
对回合中的每一步:
执行动作A~π(S)
观察下一状态S'和奖励R
w ← w + α[R + γv̂(S',w) - v̂(S,w)]∇v̂(S,w)
S ← S'
直到S是终止状态
5. 线性函数逼近
线性函数是最简单的函数逼近的方式函数了,
5.1 基本形式
v
^
(
s
,
w
)
=
w
T
⋅
x
(
s
)
=
∑
i
w
i
⋅
x
i
(
s
)
v̂(s,w) = w^T·x(s) = \sum_i w_i·x_i(s)
v^(s,w)=wT⋅x(s)=∑iwi⋅xi(s)
其中:
- x(s)是状态s的特征向量
- w是权重向量
X(s)到底是什么特征向量,这里没有解释的原因是因为后面有很多种特征向量的表达的方法,可以先耐着性子看看普遍的情况的一些方法的推导
5.2 特点
- 梯度简单:∇v̂(s,w) = x(s), 偏导数的问题很容易得到的公式对于w1的参数,和他的有关的导数就是x(1),那么整体的偏导数就是(x(1)…x(d)),正好就是s状态的x的表达式的本身
- 更新规则简化为:
w t + 1 = w t + α [ R t + 1 + γ w t T ⋅ x ( S t + 1 ) − w t T ⋅ x ( S t ) ] x ( S t ) w_{t+1} = w_t + α[R_{t+1} + γw_t^T·x(S_{t+1}) - w_t^T·x(S_t)]x(S_t) wt+1=wt+α[Rt+1+γwtT⋅x(St+1)−wtT⋅x(St)]x(St)
5.3 收敛性
- 在线性函数逼近下,TD(0)保证收敛
- 收敛到一个接近最优解的解
- 收敛性的证明涉及到了一个矩阵正定的情况的证明,用到了我们前面说到的u的稳态分布的情况,有兴趣的同学可以仔细的研读一下证明的过程,这里就不放出来了
5.4 n步TD
这里的推导也是很自然的扩展,G_t变成了n步的真实收益和剩余的价值函数,这里依然是一个半梯度的情况,因为剩余的s的价值函数还是一个关于w的函数,但是这里就不继续细说了
6. 特征构建
6.1 常用特征类型
- 多项式特征
- 原始状态值的幂
- 例如:x(s) = [1, s, s², s³]
这里原文中的有一个表达的方法和数学的表达的方法很不一样,比如k个的n阶的概念,在数学上,我们认为的是所有的k维参数的阶数的和不超过n,但是原文中的意思是每一维的参数的阶数不超过n,那么显然,每个参数有n+1个选择,习题中的(n+1)^k也就是这么来的
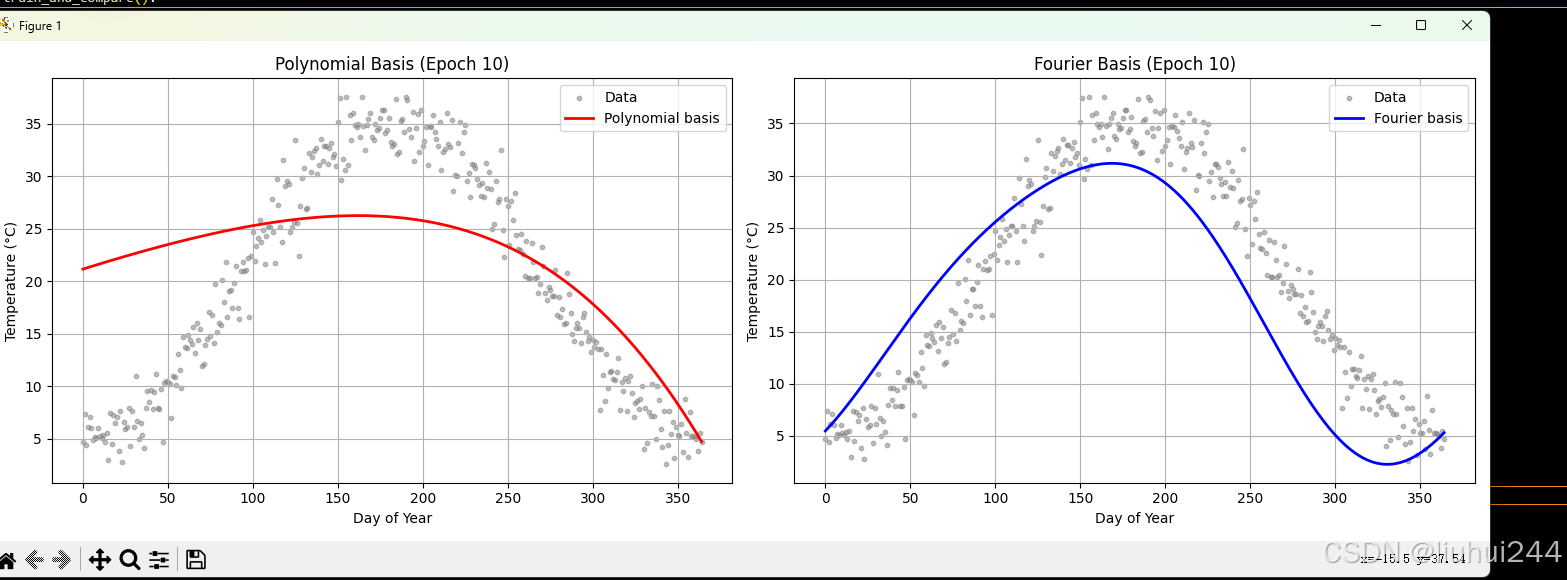
- 傅里叶特征
说真的,我的傅里叶的水平很一般,但是我知道这个适合于周期的模式,也知道傅里叶变换可以模拟任意函数(原文)。- 使用三角函数
- 适合周期性模式
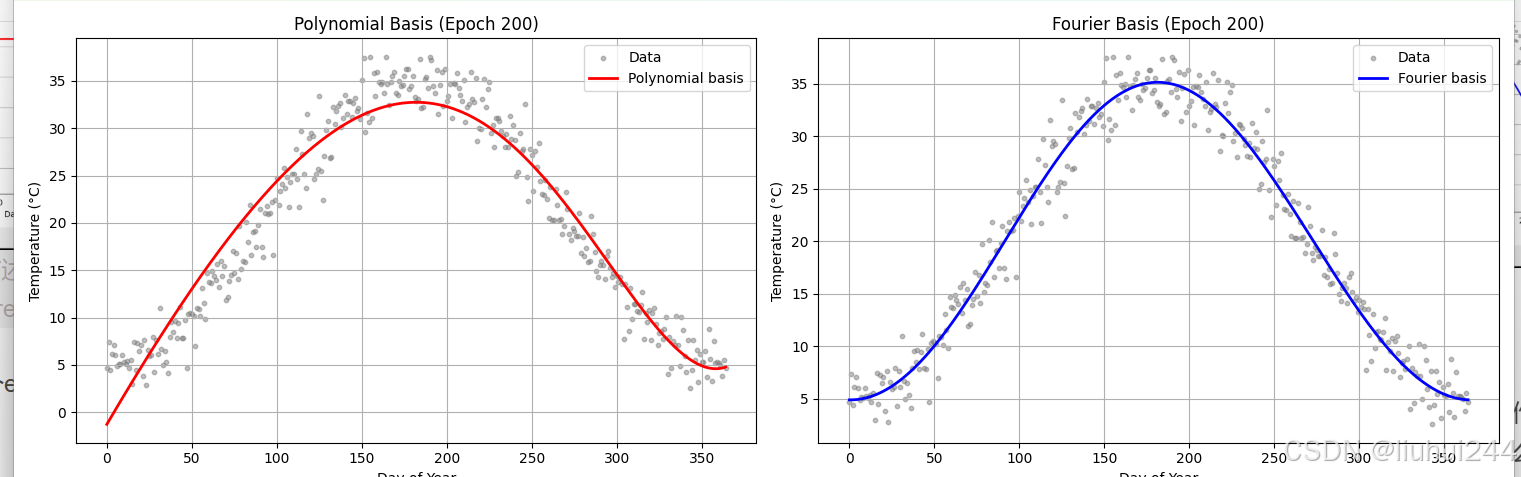
这是我假设了一个周期性变化的年度的日期的温度的一个预期的情况,在多项式和傅里叶变化上的一个函数模拟的学习的结果,可以明显看到傅里叶函数对于这种周期性的温度的变动的模拟的更加的好,预测的也会更加的准确。
每天的温度获取是这样的
def generate_temperature_data(n_days=365):
"""生成模拟的年度温度数据"""
days = np.arange(n_days)
# 基础温度曲线(年度周期)
base_temp = 20 + 15 * np.sin(2 * np.pi * days / 365 - np.pi/2)
# 添加每日波动
daily_variation = 5 * np.sin(2 * np.pi * days / 1)
# 添加随机噪声
noise = np.random.normal(0, 2, n_days)
temperatures = base_temp + daily_variation + noise
return days, temperatures
考虑到股市的周期性,使用傅里叶的变化是不是可以学习到良好的大环境的周期性的因素的学习
但是如果超过200个epoch以后,基本上都能模拟的比较类似,本来也可以通过多项式来模拟一些简单的三角函数的的关系
我
我其实真的感觉原文中的例子的对于强化学习的讲解感觉很奇怪,没有那种实际的例子,感觉是一种很学术的为了证明例子有效果的例子,我不太喜欢这种例子的方式
-
粗编码
粗编码有点像是集合的感觉了,小时候的数学题,3个写了数学作业,5个写了语文作业,2个写了英语作业的那种,如果一个人三门都写了,那么他应该是谁呢?比如学习了一个写了英语作业的人的英语的考试成绩是A,那么我们认为大概率写了英语作业的人的考试成绩都不会太差,这就是一个合理的粗编码的特征的学习- 将连续空间分割成重叠区域
- 每个特征表示状态是否在某个区域内
-
瓦片编码
瓦片编码这里有的像是我们后面的可能会学习到的卷积的感觉了,原文中的描述我感觉反正是很难看懂,如果你觉得你理解的很透可以尝试回答一下我的下面的概念的问题
- 什么叫做:状态聚合
- 什么叫做:感受野
- 定义里面哪里说明了:一个覆盖的各个瓦片是不能重叠的
- 原文图中的四个加粗的瓦片的特征的到底是什么
- 瓦片编码的维度和什么相关?
我理解的是这样的,我们可以有多层的编码,其中每一层的编码都是不能互相覆盖的,每层可能有很多个瓦片,每层的瓦片对应于其他层的一点点偏移,然后我们每一层则返回一个数字,表示我们被哪个瓦片给覆盖了,瓦片的层数,注意是层数,对应于x(s)的特征向量
原文中的4个特征表示的是4层,然后444我理解的是因为每个格子是
4
∗
4
4*4
4∗4,原文是一个
16
∗
16
16*16
16∗16的格子,需要
(
16
/
4
∗
16
/
4
)
(16/4*16/4)
(16/4∗16/4)个
瓦片,所以是
4
∗
16
4*16
4∗16,但是每一个点只有4个瓦片是激活的,每层对应一个瓦片激活
我要再次吐槽一下原文的描写例子我是完全看不懂,我也不知道原文中的8个覆盖为什么有64个独立影响的泛化区域,也 不知道为什么均匀的偏移会在对角线产生巨大的影响
原文中提到,对于一个边长的例子,我们使用了非对称的偏移函数比如(1,3),或者其他的覆盖模式,不同的长度,不同的形状理所当然得回导致不同的泛化的能力,同时我们可以多层,每层使用不同的泛化的形状, 不规则的移动的方法,来实现覆盖确保在各种维度上的特征信息能被正确学习
另一种瓦片的方式是hash,这个也很好理解,分到同一个hash的值的格子可以认为是一类,当然适用于使用hash模式的瓦片分类
6.2 选择建议
- 特征应该能捕捉问题的关键属性,例如周期性,线性、分类的特性等等
- 需要在表达能力和计算复杂度间权衡
- 可以组合多种特征
7. 实践注意事项
7.1 步长选择
- 线性情况:可以用较大步长
- 非线性情况:需要较小步长
- 可以使用自适应步长
7.2 特征归一化
- 将特征缩放到相似范围
- 有助于提高学习稳定性
8:非线性函数逼近:人工神经网络
8.1 神经网络初探
人工神经网络ANN,如果你对深度学习有基本的了解,这里深入的了解需要多深度强化学习的部分可能会讲解,我这里只是解释下最基本的原理
一个神经网络我们分为很多层,为了简单的讲解,我们使用了前向神经网络,而不是循环神经网络,也就是每个格子应该只向前去计算
对于一个n维的输入环境,例如20维,我们第一层网络是20*15的,表示的是20个输入将会对应的到15个输出,那么参数一共有30个,其中每个参数表示输入参数i对于输出参数j的权值,注意,这个时候依然是一个线性的变换
然后我们使用激活函数对于这个输出进行一次变化(通常是非线性的),例如sigmoid, softmax, Relu或 tanh等函数,这样一层就计算完毕了
然后一直到最后一层输出,例如输出到10个动作,表示的是选择这个动作的概率值
8.2 反向传播 随机梯度下降
反向梯度下降,显然我们可以计算出来每个函数的反向梯度,自然而然的针对灭一层的w权重进行更新,反向传播会使用偏导数,如果层数过多,则很有可能会导致梯度爆炸,就像前面我们学习到的重要度采样函数一样,会导致无界进而导致无法收敛,NN网络经过了很多的优化解决这些问题
8.3 过拟合
test用例数据量不够的时候,因为神经网络的参数特别多,完全可能学习到所有的VE直接=0,例如我们有200个参数,但是只有50个更新的时候,我们完全可以使用排序输出的值是目标值的情况,但是这样并不适合泛化,也不是我们学习这些参数的原因
过拟合的问题,可以通过dropout ,交叉验证,正则还,参数共享等方法来进行优化
dropout每次随机的丢弃一些神经元不参与计算,则有效的避免了某些神经元上的过拟合的问题,确保了学习的泛化能力的
逐层训练的方法,通过逐层的无监督训练每一层的数据,可以聚焦于当前的层的学习的能力,原文中说,这样比随机初始化的参数值开始训练要好,因为各层的参数已经收敛到了一个适合学习的范围
8.4 批量归一化
前面我们说过了,将所有的输入参数变成均值为0,方差为1的数据可以更好的在ANN的网络中进行学习
8.5 残差网络
ResNet,我记得原理就是连了一条旁路,可以暂时略过中间层,直接进行某层和后面的层次的全等连接。残差网络在层次很深的深度学习的过程中提升的非常明显
8.6 深度卷积神经网络
强化学习的一个很差的地方就在于s的数量太大了,如果这些s有能够得到很好的泛化,我们将会得到非常厉害的强化学习能力。学习过深度学习的同学都知道,深度学习的泛化能力是非常好的,尤其是卷积网络或者其他的学习模式等等。
卷积神经网络出现了多的东西,叫做卷积层,下采样层,卷积层用于产生特征图,例如猫的耳朵的特征,无论在图像的哪个地方,都能检查到猫耳朵的特征
下采样的常见方法:池化、stride
卷积:使用一个卷积矩阵,例如一个33,55的矩阵,实际上是一个窗口,这个窗口将会对这个窗口里面的输入的参数进行权值相加,计算完毕得到一个R实数,作为一个矩阵的变量,然后这个窗口继续向右和向下移动
pooling层这是将一个
我们按照书上的例子9.15来举例说明下他们是如何进行运算的
注意6@1414到16@1010的模式转换里面用于到了特殊的转换模式
下采样或者池化,是为了降低分辨率,可以通过平均值的方式来获得一个池化的采样
这里这是做一个大概的介绍,后面的章节会做更加细致的讲解
9:最小二乘时序差法(LSTD)
最小二乘法应该算是机器学习中的一种方法,简单来说,让我们跳过中间的学习过程,直接使用矩阵求解的方法来得到一个具体的矩阵使得我们的误差最小,
w T D = A − 1 b w_{TD} = A^{-1}b wTD=A−1b 对于任意时刻的 A t = ∑ k = 0 t − 1 x k ( x k − γ x k + 1 ) T + ϵ I A_t = \sum_{k=0}^{t-1}x_k(x_k - \gamma x_{k+1})^T + \epsilon I At=∑k=0t−1xk(xk−γxk+1)T+ϵI, b ^ t = ∑ k = 0 t − 1 R t + 1 x k \hat b_t = \sum_{k = 0}^{t-1}R_{t+1}x_k b^t=∑k=0t−1Rt+1xk
最小二乘时序差分的最核心的内容我觉得就是增量式更新
前面的A的求和函数,展开可得
A
^
t
=
A
^
t
+
1
+
x
t
−
1
(
x
t
−
1
−
γ
x
t
)
\hat A_{t} = \hat A_{t+1} + x_{t-1}(x_{t-1} - \gamma x_t)
A^t=A^t+1+xt−1(xt−1−γxt),那么更新公式里面的A逆矩阵的就是上面展开式的逆矩阵
根据Sherman-Morrison的算法公式展开
令
u
=
x
t
−
1
,
v
=
(
x
t
−
1
−
γ
x
t
)
令u = x_{t-1},v = (x_{t-1} - \gamma x_t)
令u=xt−1,v=(xt−1−γxt)
令
B
=
(
A
+
u
v
T
)
令 B = (A + uv^T)
令B=(A+uvT)
令
C
=
A
−
1
−
(
A
−
1
∗
u
v
T
A
−
1
)
(
1
+
v
T
A
−
1
u
)
令 C = A^{-1} - \frac{(A^{-1}*uv^TA^{-1})}{(1 + v^TA^{-1}u)}
令C=A−1−(1+vTA−1u)(A−1∗uvTA−1)
B
C
=
(
A
+
u
v
T
)
[
A
−
1
−
(
A
−
1
u
v
T
A
−
1
)
(
1
+
v
T
A
−
1
u
)
]
BC = (A + uv^T)[A^{-1} - \frac {(A^{-1}uv^TA^{-1})}{(1 + v^TA^{-1}u)}]
BC=(A+uvT)[A−1−(1+vTA−1u)(A−1uvTA−1)]
= A A − 1 + u v T A − 1 − [ A A − 1 u v T A − 1 ] ( 1 + v T A − 1 u ) − [ u v T A − 1 u v T A − 1 ] ( 1 + v T A − 1 u ) = AA^{-1} + uv^TA^{-1} - \frac {[AA^{-1}uv^TA^{-1}]}{(1 + v^TA^{-1}u)} - \frac {[uv^TA^{-1}uv^TA^{-1}]}{(1 + v^TA^{-1}u)} =AA−1+uvTA−1−(1+vTA−1u)[AA−1uvTA−1]−(1+vTA−1u)[uvTA−1uvTA−1]
关键点来了,需要注意的是,此时的 v T A − 1 u v^TA^{-1}u vTA−1u是一个一维的数字可以随意的变化位置
= I + u v T A − 1 − [ u v T A − 1 ] ( 1 + v T A − 1 u ) − [ u v T A − 1 ( v T A − 1 u ] ) ( 1 + v T A − 1 u ) = I + uv^TA^{-1} - \frac {[uv^TA^{-1}]}{(1 + v^TA^{-1}u)} - \frac {[uv^TA^{-1}(v^TA^{-1}u])} {(1 + v^TA^{-1}u)} =I+uvTA−1−(1+vTA−1u)[uvTA−1]−(1+vTA−1u)[uvTA−1(vTA−1u])
= I + u v T A − 1 − [ u v T A − 1 ( 1 + v T A − 1 u ) ] ( 1 + v T A − 1 u ) = I + uv^TA^{-1} - \frac{[uv^TA^{-1}(1 + v^TA^{-1}u)]}{(1 + v^TA^{-1}u)} =I+uvTA−1−(1+vTA−1u)[uvTA−1(1+vTA−1u)]
=
I
证明完毕
= I 证明完毕
=I证明完毕
显然如果已经有了A的逆,u,v那么一次运算只是d^2的算法复杂度
伪代码不放了,更新A的逆就已经不说了,b使用RX来更新,w直接使用计算好的A的逆和b相乘即可
10.基于记忆的函数逼近
基于记忆的方法其实很好理解,有点像是机器学习里面的KNN算法,最邻近的K的邻居的值,比如我们假设一个函数是连续的,比如假设是y=x^2,那么显然一个点周围的点的值(来自于样本的真实返回)显然可以用来估测当前节点的输出值,
算法的核心在于查找与查询状态的最近的K邻居节点的距离,加权平均法,使用距离作为权值来进行计算
原文说明的和我前面的描述一致,做一个曲面的拟合,然后计算出来拟合的函数,然后输出当前的值,然后丢弃这个曲面,因为下面的选取的点,将会生成一个新得到曲面
显然这个有点像是稀疏转换的情况,不需要那么多的用例来进行学习
核心的地方,使用了k-d维数,保存一个d维的k个最近的节点的状态,搜索可以变得更快。
11. 基于核函数的函数逼近
刚刚说的基于距离的权值的函数,我们称之为kernel核函数,k(s,s`)是查询s的时候,分配给s’的权值,但是注意这个权值是一个函数来实现的,不一定基于距离。
我喜欢原文中的这句话,k表示s’对于s泛化能力的度量
核函数回归,使用k函数来讲所有的s’的进行加权来测量s的价值函数,显然这是一个可偏导的函数
核函数不想讲了,但是原理就是这么个原理。
12. 兴趣与强调
兴趣就是对于一个状态的关心的程度,兴趣值可以认为是前面的
μ
\mu
μ分布的一个权值,
强调值表示的是
当前的兴趣程度
+
γ
∗
上一个强调值
当前的兴趣程度 + \gamma * 上一个强调值
当前的兴趣程度+γ∗上一个强调值
强调值是用来扩展学习率alpha的,所以是每次更新的时候使用的,不像是
γ
\gamma
γ,用在每次的reward,强调值用在每次更新的计算一次