floodfill

floodfill 算法又被称为洪水灌溉算法，本质上就是一种暴力搜索算法。

下面我来带领大家感受一些这个算法在题目中的使用。

实战演练

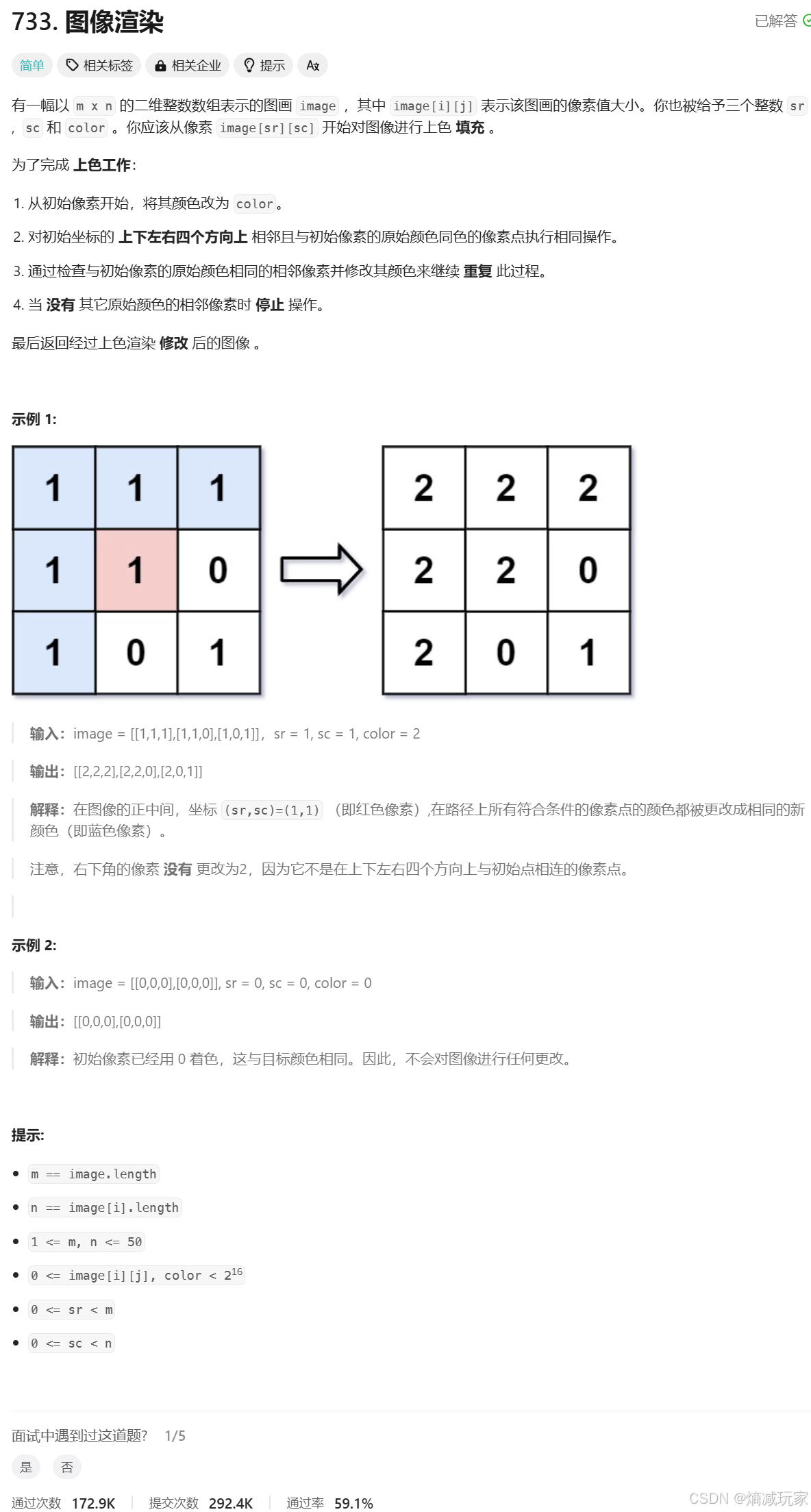
图形渲染

https://leetcode.cn/problems/flood-fill

解析：
题意解读：当我们的起始位置的颜色与需要设置的目标颜色一致的时候，我们不用做任何的修改，也就是可以不进行搜索了。
如果起始位置和目标颜色不一致，我们需要把它周围和它一样的颜色的像素块改成目标颜色，所以我们在修个这个起始位置的像素块的时候，我们要先保存记录，方便后续搜索。

如何搜索？？？
我们要从起始位置开始向上下左右四个方向进行搜索，这里我们可以定义向量组，int[] dx = {0, 0, 1, -1};int[] dy = {1, -1, 0, 0}; 方便我们遍历四个方向进行深度搜索，下面的题目也是以深搜为例讲解。

然后开始关心其中一个像素块在做什么？这就是子问题，递归的函数体。
首先从这个位置看看四个方向有没有要修改的，如果有就进入它进行下一个递归。所以这里使用 for 循环，循环四次把四个方向遍历到，进行判断（下标不能越界还有这个方块是和起始位置的颜色是一致的）进入递归。

每次进入递归的时候，我们顺便把方块的数值进行修改即可。

class Solution {
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};
    int m, n, color, find;
    public int[][] floodFill(int[][] image, int sr, int sc, int _color) {
        m = image.length;
        n = image[0].length;
        color = _color;
        if(image[sr][sc] != color) {
            find = image[sr][sc];
            dfs(image, sr, sc);
        } 
        return image;
    }
    void dfs(int[][] image, int i, int j) {
        image[i][j] = color;
        for(int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == find) {
                dfs(image, x, y);
            } 
        }
    }
}

岛屿数量

https://leetcode.cn/problems/number-of-islands

解析：
首先岛屿只能由上下左右四个方向的陆地进行连接，所以我们可以先设置向量组，方便后续的遍历。
接着我们遍历所有的地区，当遇到陆地的时候，进行深搜，把和它相邻的陆地找到并都修改为 0，这样这一块岛屿就被销毁了，计数器也随机加 1，当所有的方块遍历完毕，岛屿数量也就出来了。

class Solution {
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};
    int m, n;
    public int numIslands(char[][] grid) {
        int count = 0;
        m = grid.length;
        n = grid[0].length;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(grid[i][j] == '1') {
                    dfs(grid, i, j);
                    count++;
                }
            }
        }
        return count;
    }
    void dfs(char[][] grid, int i, int j) {
        grid[i][j] = '0';
        for(int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == '1') {
                dfs(grid, x, y);
            }
        }
    }
}

岛屿的最大面积

https://leetcode.cn/problems/max-area-of-island

解析：
我们找到所有的岛屿，并记录好该岛屿的面积，然后进行比较就可以得到最大的面积值。

class Solution {
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};
    int m, n, sum, count;
    public int maxAreaOfIsland(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(grid[i][j] == 1) {
                    dfs(grid, i, j);
                    sum = Math.max(sum, count);
                    count = 0;
                }
            }
        }
        return sum;
    }
    void dfs(int[][] grid, int i, int j) {
        grid[i][j] = 0;
        count++;
        for(int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                dfs(grid, x, y);
            }
        }
    }
}

被围绕的区域

https://leetcode.cn/problems/surrounded-regions

解析：
题意分析：首先一个区域的定义是这个区域是由上下左右这四个方向的 O 方块组成的，所以我们要想遍历某个区域，就得把这四个方向都搜索一遍，这里我们就可以使用向量组。

被围绕的区域是指这个区域的上下左右四个方向都被 X 给包围了，如果这个区域是被包围的，那就要把这个区域所有的 O 修改为 X

如何搜索？？？
如果你想暴力所有的方块，也就是把所有的区域都找到，然后从中找到被包围的区域，你会发现做起来很麻烦，因为你的区域需要标记要么原地标记要么再开一个数组来作为标记数组，之后如果发现这个区域没有被包围，那就需要回溯的时候还原现场，特别麻烦

既然正着来做，我们就反着做，这就是正难则反，也是逆向思维的体现。

因为没有被包围的区域一定存在每个或者某些方块是位于数组的边缘地带，所以我们可以把数组的边缘给遍历一遍，找到 O 方块，然后对其进行深搜，把这个没有被包围的区域找到并标记起来，这里我直接在原数组进行标记，把没有被包围的区域用 . 给标记起来。

等到边缘地区都被搜索完成之后，我们对整个数组进行一次遍历，把所有 O 修改为 X，所有 . 还原为 O

这样就完成了任务。

class Solution {
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};
    int m, n;
    public void solve(char[][] board) {
        m = board.length;
        n = board[0].length;
        for(int i = 0; i < m; i++) {
            if(board[i][0] == 'O') {
                dfs(board, i, 0);
            }
            if(board[i][n-1] == 'O') {
                dfs(board, i, n-1);
            }
        }
        for(int j = 0; j < n; j++) {
            if(board[0][j] == 'O') {
                dfs(board, 0, j);
            }
            if(board[m - 1][j] == 'O') {
                dfs(board, m-1, j);
            }
        }
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(board[i][j] == '.') {
                    board[i][j] = 'O';
                } else if(board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }
    void dfs(char[][] board, int i, int j) {
        board[i][j] = '.';
        for(int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O') {
                dfs(board, x, y);
            }
        }
    }
}

扫雷游戏

https://leetcode.cn/problems/minesweeper

解析：
题意分析：首先如果一开始就踩到地雷 ‘M’，那么就把这个位置修改为 ‘X’，并且直接返回

如果一开始没有踩到地雷，那我们就进行深搜，首先扫雷游戏是需要搜索一个方块周围上下左右以及对角线一共八个方向的方块，因此这个我们定义的向量组要能够覆盖到这八个方向。
当这八个方向存在地雷的时候，那么这个位置需要显示出周围一共由多少颗地雷，接着就不用继续递归展开了。
如果正好这八个方向都没有地雷，那么我们需要将这个位置修改为 ‘B’，接着向这八个方向进行深搜展开。

class Solution {
    int[] dx = {0, 0, 1, -1, 1, 1, -1, -1};
    int[] dy = {1, -1, 0, 0, 1, -1, -1, 1};
    int m, n;
    public char[][] updateBoard(char[][] board, int[] click) {
        m = board.length;
        n = board[0].length;
        int x = click[0];
        int y = click[1];
        if(board[x][y] == 'M') {
            board[x][y] = 'X';
        } else {
            dfs(board, x, y);
        }
        return board;
    }
    void dfs(char[][] board, int i, int j) {
        int count = 0;//标记此时周围的地雷数量
        for(int k = 0; k < 8; k++) {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'M') {
                count++;
            }
        }
        if(count != 0) {
            board[i][j] = (char)('0' + count);
        } else {
            board[i][j] = 'B';
            for(int k = 0; k < 8; k++) {
                int x = i + dx[k], y = j + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'E') {
                    dfs(board, x, y);
                }
            }
        }
    }
}

衣橱整理 (机器人的运动范围)

https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof

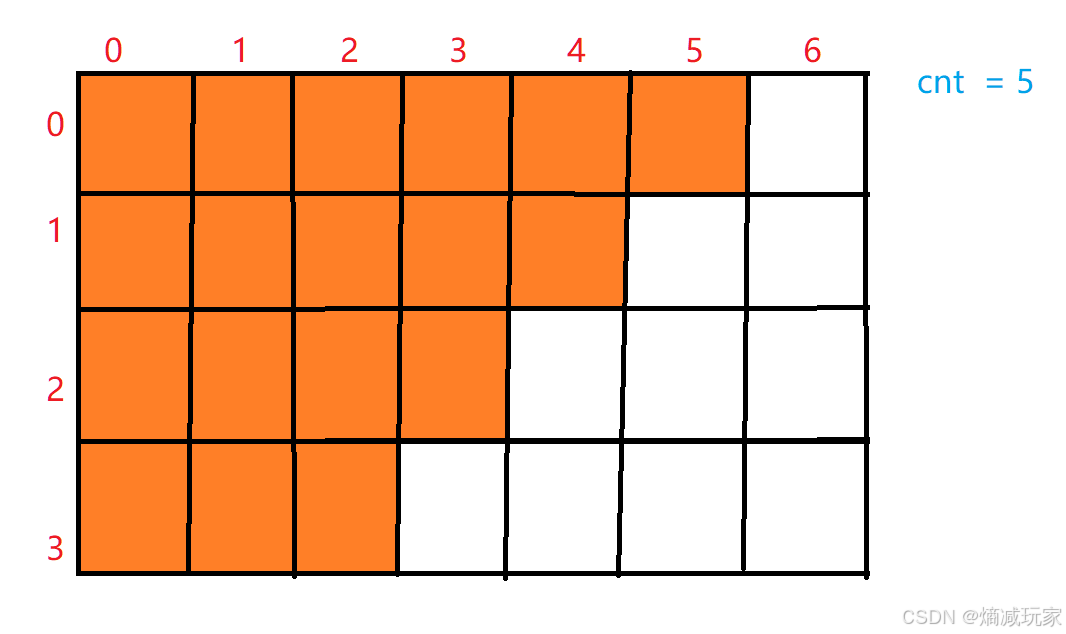
题目解析：这里要注意我们要求的是家具整理师的运动范围，当遇到不用整理的格子的时候，我们不能进入这个方块内，当遇到可以整理的方格的时候我们可以进入并且下一次的运动方向是向下或者向右，我们需要求的是运动范围的大小，相信看到这里大家已经知道怎么做了。

首先我们先定义向量组，然后创建一个方法 digit(int x) 来统计 x 的各位数字之和，再创建一个标记数组标记该位置是否来过。
接下来就是从 （0，0）这个位置开始进行深搜。

class Solution {
    int[] dx = {0, 1};
    int[] dy = {1, 0};
    int m, n, count;
    boolean[][] check;
    public int wardrobeFinishing(int _m, int _n, int cnt) {
        m = _m;
        n = _n;
        check = new boolean[m][n];
        dfs(0, 0, cnt);
        return count;
    }
    void dfs(int i, int j, int cnt) {
        count++;
        check[i][j] = true;
        for(int k = 0; k < 2; k++) {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && !check[x][y] &&
            digit(x) + digit(y) <= cnt) {
                dfs(x, y, cnt);
            }
        }
    }
    int digit(int x) {
        int sum = 0;
        while(x != 0) {
            sum += (x % 10);
            x /= 10;
        }
        return sum;
    }
}