[NOIP2002 普及组] 级数求和

题干

题目描述

已知：$S_n=1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}$。显然对于任意一个整数 $k$，当 $n$ 足够大的时候，$S_n>k$。

现给出一个整数 $k$，要求计算出一个最小的 $n$，使得 $S_n>k$。

输入格式

一个正整数 $k$。

输出格式

一个正整数 $n$。

样例 #1

样例输入 #1

1

样例输出 #1

2

提示

【数据范围】

对于 $100\%$ 的数据，$1\le k\le 15$。

【题目来源】

NOIP 2002 普及组第一题

思路

这是第一题，所以比较简单。
看到数据范围，我们可以发现，$k$ 较小，$1\le k\le 15$，所以我们可以直接暴力枚举。
而怎么存储 $1/i$ 的值呢？我们只需要使用 $double$ 即可，它是一种浮点数（小数）类型，用于进行小数计算。
再用一个 $double$ 变量 $ans$ 去存储 $1-i$ 之间 $1/i$ 的和，每增加一次就判断一次它是否大于 $k$ ，如果大于 $k$ ，输出当前的 $i$ 即可。
如：$k=1$
$i=1:ans+=1/1;(ans=1)ans=1=1$
$i=2:ans+=1/2;(ans=1.5)ans=1.5>1$
$输出答案为：2$

代码

#include <stdio.h>
double ans ;
int k,i ;
int main(){
	scanf("%d",&k) ;
	//输入
	while(ans <= k) ans += 1.0 / (++ i) ;
	//求和直到ans > k
	printf("%d",i) ;
	//输出i
	return 0 ;
}

[NOIP2002 普及组] 选数

题干

题目描述

已知 $n$ 个整数 $x_1,x_2,\cdots ,x_n$，以及 $1$ 个整数 $k$（$k<n$）。从 $n$ 个整数中任选 $k$ 个整数相加，可分别得到一系列的和。例如当 $n=4$，$k=3$，$4$ 个整数分别为 $3,7,12,19$ 时，可得全部的组合与它们的和为：

$3+7+12=22$

$3+7+19=29$

$7+12+19=38$

$3+12+19=34$

现在，要求你计算出和为素数共有多少种。

例如上例，只有一种的和为素数：$3+7+19=29$。

输入格式

第一行两个空格隔开的整数 $n,k$（$1\le n\le 20$，$k<n$）。

第二行 $n$ 个整数，分别为 $x_1,x_2,\cdots ,x_n$（$1\le x_i\le 5\times 10^6$）。

输出格式

输出一个整数，表示种类数。

样例 #1

样例输入 #1

4 3
3 7 12 19

样例输出 #1

1

提示

【题目来源】

NOIP 2002 普及组第二题

思路

观察范围可得：输入的数据一般，数据个数较小。
所以我们可以直接模拟在 $n$ 个数里面取 $k$ 个数的情况，再判断这种情况所求出来的和是不是质数即可。
为了避免重复，我们可以使用“单向选取法”，即确定了前面有哪些数是取的以后，就不在改变前面的选择，而通过后面数的选与不选求出更多情况。
如：
$4$ $2$
$3$ $7$ $12$ $19$
确定选 $3$ 以后，还可选 $7$ $12$ $19$
若不选 $3$ 且确定选 $7$ 以后，还可选 $7$ $12$ $19$ 。
若不选 $3、7$ 且确定选 $12$ 以后，还可选 $19$ 。
若不选 $3、7、12$，因为只有一个数 $19$ 了，所以没有合法的情况。

代码

#include <bits/stdc++.h>
using namespace std ;
bool is_prime(int t){
	if(t < 2)return false ;
	//如果是0、1或负数，则不是质数
	if(t < 4)return true ;
	//如果是2、3则是质数
	if((t % 6) != 1 && (t % 6) != 5)return false ;
	//如果 (t % 6) 为 0 2 4 时为 2 的倍数
	//如果 (t % 6) 为 3 时为 3 的倍数
	//所以一个质数（除2、3外），取余6的结果只能为1、5
	const int end = sqrt(t) + 1 ;
	//一个合数最大的质因子只能为它的开平方
	for(int i = 2;i < end;++ i)
		//循环判断这个数是否有除1、自身外的因子
		if(!(t % i))return false ;
		//如果有，返回 false
	return true ;
	//否则，返回true
}
int x[25],n,k,ans,all ;
//变量定义
void hs(int pos,int num,int s){
	//表示当前要判断选不选的数，已经选了的个数，和当前的和
	if(num == k){
		//如果个数满了，则判断是否为质数
		if(is_prime(s))++ ans ;
		//如果是质数，答案加1
		return ;
		//返回
	}else if(pos > n) return ;
	//如果数没了，直接返回
	hs(pos + 1,num,s) ;
	//这个数不选，直接跳过
	hs(pos + 1,num + 1,s + x[pos]) ;
	//选这个数，当前个数加一，总数加一
	return ;
}
int main(){
	scanf("%d%d",&n,&k) ;
	//输入总个数及需要选出的个数
	for(int i = 1;i <= n;++ i)scanf("%d",&x[i]) ;
	//输入各个数
	hs(1,0,0) ;
	//从第一个数开始选起
	printf("%d",ans) ;
	//输出答案
	return 0 ;
}

[NOIP2002 普及组] 产生数

题干

题目描述

给出一个整数 $n$ 和 $k$ 个变换规则。

规则：

• 一位数可变换成另一个一位数。
• 规则的右部不能为零。

例如：$n=234,k=2$。有以下两个规则：

• $2⟶5$。
• $3⟶6$。

上面的整数 $234$ 经过变换后可能产生出的整数为（包括原数）:

• $234$。
• $534$。
• $264$。
• $564$。

共 $4$ 种不同的产生数。

现在给出一个整数 $n$ 和 $k$ 个规则。求出经过任意次的变换（$0$ 次或多次），能产生出多少个不同整数。

仅要求输出个数。

输入格式

第一行两个整数 $n,k$，含义如题面所示。

接下来 $k$ 行，每行两个整数 $x_i,y_i$，表示每条规则。

输出格式

共一行，输出能生成的数字个数。

样例 #1

样例输入 #1

234 2
2 5
3 6

样例输出 #1

4

提示

对于 $100\%$ 数据，满足 $n<10^{30}$，$k\le 15$。

【题目来源】

NOIP 2002 普及组第三题

思路

因为一个个位数最多有 $10$ 种情况，所以一个数字能转换成的数字最多只有 $10$ 种情况，因而可以用一个函数来计算这个数字所能转换成的数字数（包括自己）。过程如下：
首先 将一个大小为 $10$ 的标记数组全部设为 $false$
接着，设计一个递归函数：
$(1)$ 通过参数传入当前已经转换成的数字，如果这个数字已经统计过了，直接返回
$(2)$ 否则，标记该数字为 $true$ ，即原数字可以转换到该数字，随后判断当前数字能转换为什么数字，将再次转换的的数字重复第一步的操作，标记数组不清零（即统计能间接转换到的数字）
$(3)$ 统计标记数组中有多少个数字标记成了 $true$ ，结果就是 $true$ 的个数
同时原数字中的一位数字也是最多对应十种情况，所以最多有 $30\ast 10=100$ 位数字，而原数字的大小也超过了 $longlong$ 的最大范围，所以只能使用字符串来存储原数字，再使用大数算法计算原数各个位的可能性相乘的结果即可（高精乘低精）

代码

#include <bits/stdc++.h>
using namespace std ;
char s[35] ;
//用来储存原数的字符串
int k,times[10],x,y ;
//一些变量
bool all[10],a[10][10] ;
//一些变量
int ans[305],size = 1 ;
//储存答案的大数和大数的当前长度
void func(int which){
	if(all[which])return ;
	//如果当前数字已经标记了，则直接返回
	all[which] = true ;
	//否则直接标记
	for(int i = 0;i < 10;++ i)
		//标记能够间接转换的数字
		if(a[which][i])func(i) ;
	//返回
	return ;
}
int get(int now){
	//如果当前数字的答案已经计算过了，则直接返回，不重复计算
	if(times[now])return times[now] ;
	//清零标记数组
	for(int i = 0;i < 10;++ i)all[i] = false ;
	//开始标记
	func(now) ;
	//标记完成，统计能够转换成的数字的个数
	for(int i = 0;i < 10;all[i] = false,++ i)
		//如果一个数字标记到了，则统计上
		if(all[i])++ times[now] ;
	//返回结果
	return times[now] ;
}
int main(){
    scanf("%s%d",s,&k) ;
    //输入变量
    while(k --)scanf("%d%d",&x,&y),a[x][y] = 1 ;
    //输入转换关系
    ans[0] = 1 ;
    //大数类初始化
    for(int i = 0;s[i];++ i){
    	for(int o = 0;o < size;++ o)
    		ans[o] *= get(s[i] - '0') ;
    	//每一位乘以这一位的可能的情况数
    	for(int o = 0;o < size;++ o)
    		//进位操作
    		ans[o + 1] += ans[o] / 10,ans[o] %= 10 ;
    	//进位操作
    	while(ans[size])ans[size + 1] += ans[size] / 10,ans[size ++] %= 10 ;
	}
	//反向输出大数类，正向输出答案
    for(int i = size - 1;i >= 0;-- i)
    	//一位一位输出
    	putchar(ans[i] + '0') ;
    return 0 ;
}

[NOIP2002 普及组] 过河卒

题干

题目描述

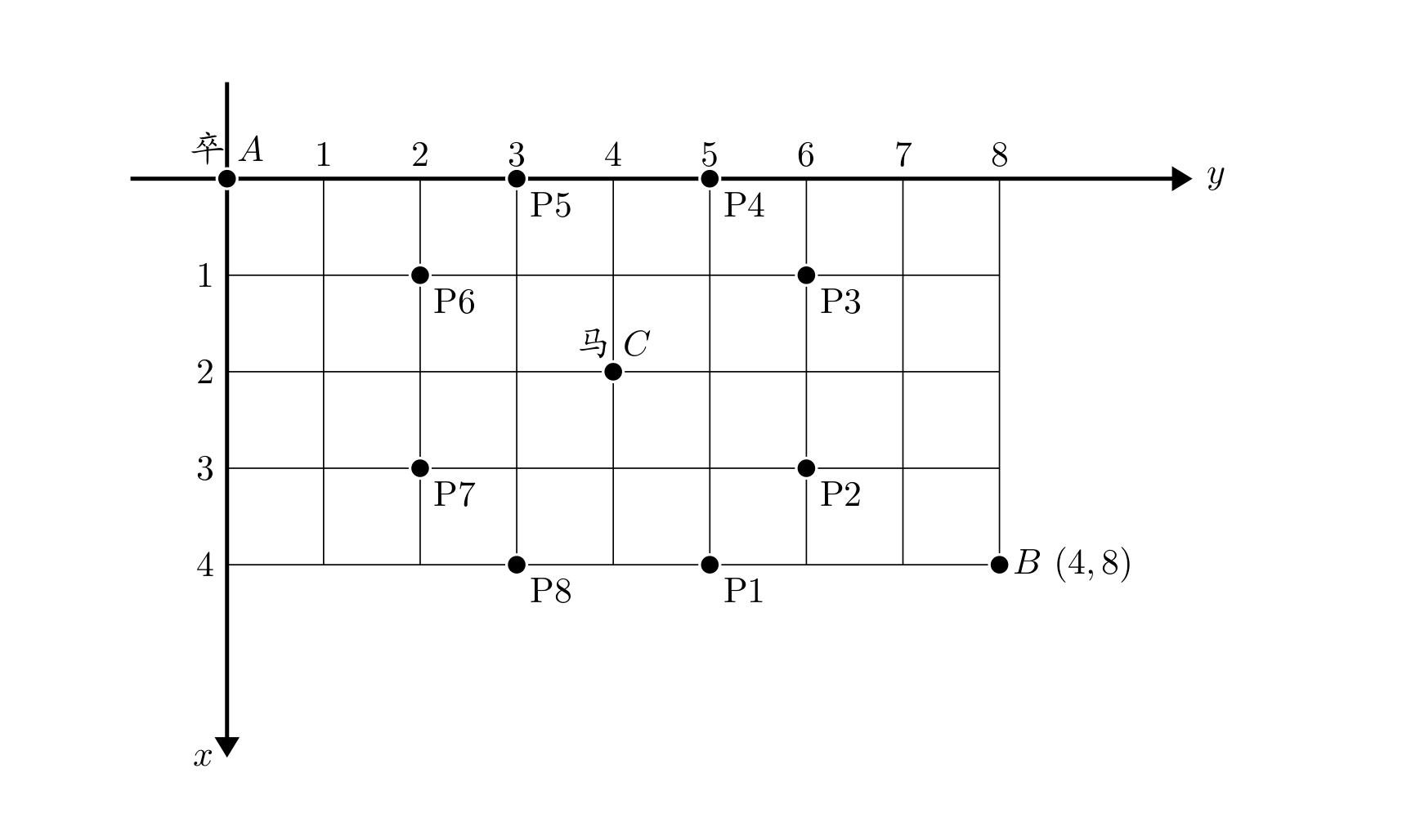
棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0,0)$、$B$ 点 $(n,m)$，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于 $100\%$ 的数据，$1\le n,m\le 20$，$0\le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

思路

这一题就是一个标准 $dp$ 问题。
这一题我们可以发现，如果一个点被马控制了的话，那么它的值就会为 $0$ （终点、起点除外）
否则，它的值为走到它上方格子的情况数再加上走到它下方格子的情况数。$(状态转移方程)$
而判断一个格子 $（i,o）$ 是否是码的控制点，有两种情况：（终点、起点除外）
$（1）$ 该点就是马所在的点
$（2）$ 该点的纵坐标和横坐标与纵坐标和横坐标，其中一个相差 $1$ ，其中一个相差 $2$ 。则它们的曼哈顿距离（纵坐标之差与横坐标之差的和）一定为3，且纵、横坐标均不相等

代码

#include <stdio.h>
typedef long long ll ;
ll abs(ll x){ return (x < 0) ? (-x) : (x) ; }
//取绝对值
ll n,m,x,y,a[25][25] ;
//一些变量
int main(){
    scanf("%lld%lld%lld%lld",&n,&m,&x,&y) ;
    //输入变量
    a[0][0] = 1 ;
    //起点不能被控制
    for(ll i = 0;i <= n;++ i)
    	for(ll o = 0;o <= m;++ o){
    		if(!i && !o)continue ;
    		//起点不能被控制
    		if(!(((i == x && o == y)) || 
				(((abs(i - x) + abs(o - y)) == 3) && (i != x) && (o != y)))){
				//如果该点不被控制
				if(i)a[i][o] = a[i - 1][o] ;
				//如果有上点，则增加上点的情况数
				if(o)a[i][o] += a[i][o - 1] ;
				//如果有左点，则增加左点的情况数
			}
		}
	printf("%lld",a[n][m]) ;
	//输出走到终点的情况数
    return 0 ;
}

尾声

又成功地“秒杀”了一年的CSP/NOIP，祝读者水平高升，参加竞赛都能“秒杀”取得好成绩！