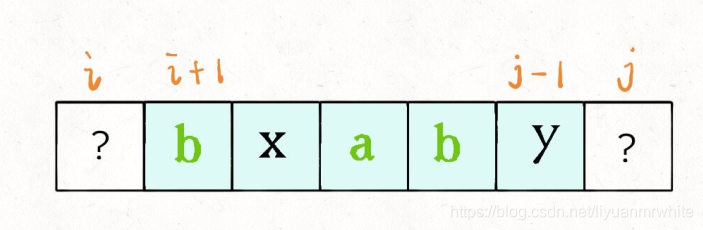问题描述:516. 最长回文子序列
给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1:
输入:
"bbbab"
输出:
4
一个可能的最长回文子序列为 "bbbb"。
示例 2:
输入:
"cbbd"
输出:
2
一个可能的最长回文子序列为 "bb"。
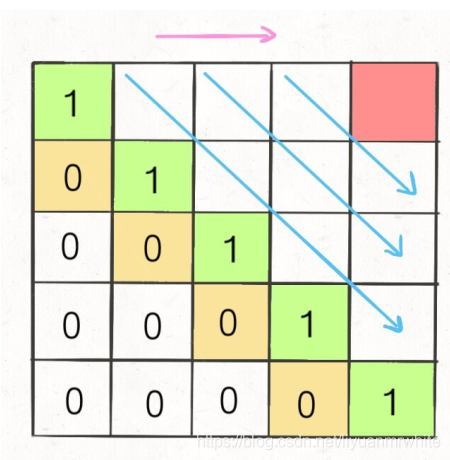
方法一:斜线遍历
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
dp = [[0]*(n) for i in range(n)]
for i in range(n):
dp[i][i] = 1
#l 为偏移量
for l in range(1,n):
for i in range(n-l):
j = i + l
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1]+2
else:
dp[i][j] = max(dp[i+1][j],dp[i][j-1])
return dp[0][n-1]
方法二:斜向下遍历+状态压缩
import copy
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
dp = [1 for i in range(n)]
pre = [0 for i in range(n)]
tmp = [0 for i in range(n)]
for l in range(1,n):
for i in range(n-l):
j = i + l
//每次重新开启外循环时,l-1的元素要重新赋值,获得每次外循环开始的dp[i][j-1]元素
//参考(0,1)(0,2)(0.3)(0,4)步骤 外循环新触发时元素的更新
tmp[l-1] = dp[l-1]
//获得dp[i+1][j]
tmp[j] = dp[j]
if s[i] == s[j]:
dp[j] = pre[j-1] + 2 //pre[j-1]就是dp[i+1][j-1]
else:
dp[j] = max(tmp[j-1], tmp[j])
//不能放在for内循环,因为每次都会更新pre数组,导致dp[i+1][j-1]被更新,参考(1,4)步骤
pre = copy.deepcopy(tmp)
return dp[n-1]以测试集'bbbab'为例
| l | (i,j) | tmp | dp | pre |
| 1 | (0, 1) | [1, 1, 0, 0, 0] | [1, 2, 1, 1, 1] | [0, 0, 0, 0, 0] |
| 1 | (1, 2) | [1, 1, 1, 0, 0] | [1, 2, 2, 1, 1] | [0, 0, 0, 0, 0] |
| 1 | (2, 3) | [1, 1, 1, 1, 0] | [1, 2, 2, 1, 1] | [0, 0, 0, 0, 0] |
| 1 | (3, 4) | [1, 1, 1, 1, 1] | [1, 2, 2, 1, 1] | [0, 0, 0, 0, 0] |
| 2 | (0, 2) | [1, 2, 2, 1, 1] | [1, 2, 3, 1, 1] |