二叉搜索树
1. 定义
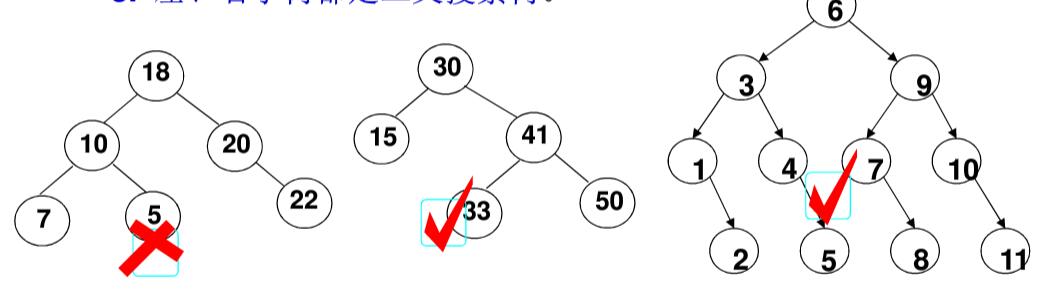
二叉搜索树(BST)也称二叉排序树或二叉查找树
二叉搜索树:一棵二叉树,可以为空;如果不为空,满足以下性质:
- 非空左子树的所有键值小于其根结点的键值
- 非空右子树的所有键值大于其根结点的键值
- 左、右子树都是二叉搜索树
2. 特殊函数
BinTree Find(ElementType X,BinTree BST):从二叉搜索树 BST 中查找元素 X,返回其所在结点地址BinTree FindMin(BinTree BST):从二叉搜索树 BST 中查找并返回最小元素所在结点的地址BinTree FindMax(BinTree BST):从二叉搜索树 BST 中查找并返回最大元素所在结点的地址BinTree Insert(ElementType X,BinTree BST):插入一个元素进 BSTBinTree Delete(ElementType X,BinTree BST):从 BST 中删除一个元素
1. 查找
- 查找从根结点开始,如果树为空,返回 NULL
- 若搜索树不为空,则根结点键值和 X 进行比较,并进行不同处理:
- 若 X 小于根结点键值,在左子树中继续查找
- 若 X 大于根结点键值,在右子树中继续查找
- 如 X 等于根节点键值,查找结束,返回指向此结点的指针
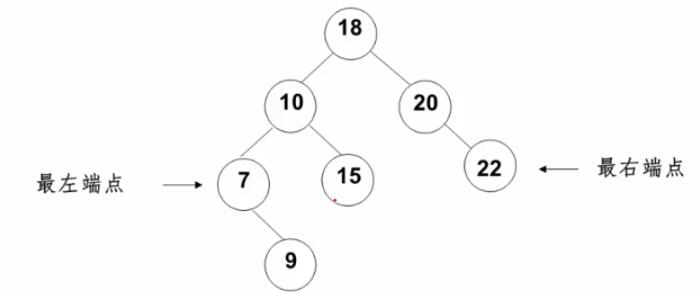
2. 查找最大和最小元素
-
最大元素一定是在树的最右分支的端结点上
-
最小元素一定是在树的最左分支的端结点上
3. 删除
删除的三种情况:
-
要删除的是叶结点:直接删除,并将其父结点指针置为 NULL
-
要删除的结点只有一个孩子结点:将其父结点的指针指向要删除结点的孩子结点
-
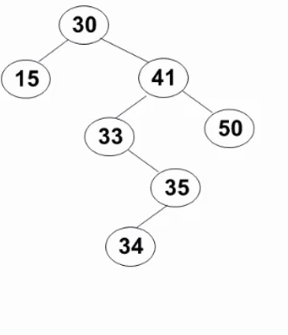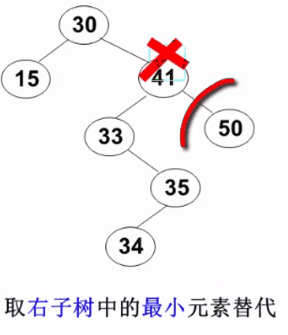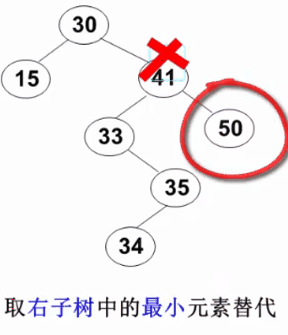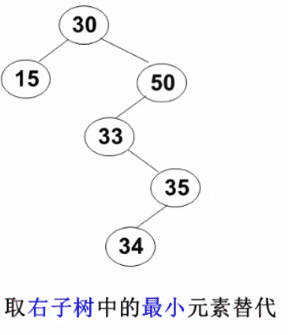
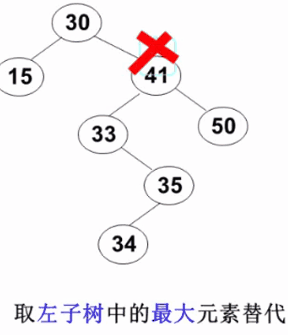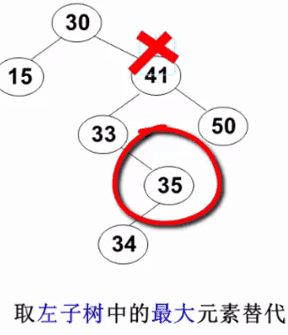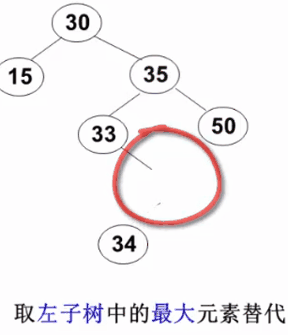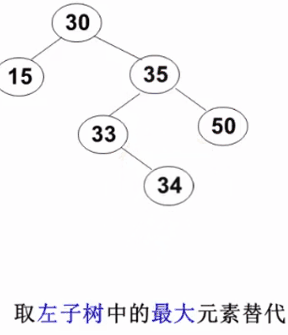
要删除的结点有左、右两棵子树:用右子树的最小元素或左子树的最大元素替代被删除结点
4. 代码实现
#include<iostream>
#include<malloc.h>
using namespace std;
typedef int ElementType;
typedef struct TreeNode *BinTree;
struct TreeNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
// 查找递归实现
BinTree Find(ElementType X,BinTree BST){
if(!BST) // 如果根结点为空,返回 NULL
return NULL;
if(X < BST->Data) // 比根结点小,去左子树查找
return Find(X,BST->Left);
else if(BST->Data < X) // 比根结点大,去右子树查找
return Find(X,BST->Right);
else if(BST->Data == X) // 找到了
return BST;
}
// 查找非递归实现
BinTree IterFind(ElementType X,BinTree BST){
while(BST){
if(X < BST->Data)
BST = BST->Left;
else if(BST->Data < X) // 比根结点大,去右子树查找
BST = BST->Right;
else if(BST->Data == X) // 找到了
return BST;
}
return NULL;
}
// 查找最小值的递归实现
BinTree FindMin(BinTree BST){
if(!BST) // 如果为空了,返回 NULL
return NULL;
else if(BST->Left) // 还存在左子树,沿左分支继续查找
return FindMin(BST->Left);
else // 找到了
return BST;
}
// 查找最大值的非递归实现
BinTree FindMax(BinTree BST){
if(BST) // 如果不空
while(BST->Right) // 只要右子树还存在
BST = BST->Right;
return BST;
}
// 插入
BinTree Insert(ElementType X,BinTree BST){
if(!BST){ // 如果为空,初始化该结点
BST = (BinTree)malloc(sizeof(struct TreeNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}else{ // 不为空
if(X < BST->Data) // 如果小,挂在左边
BST->Left = Insert(X,BST->Left);
else if(BST->Data < X) // 如果大,挂在右边
BST->Right = Insert(X,BST->Right);
// 如果相等,什么都不用做
}
return BST;
}
// 删除
BinTree Delete(ElementType X,BinTree BST){
BinTree tmp;
if(!BST)
cout<<"要删除的元素未找到";
else if(X < BST->Data) // X 比当前结点值小,在左子树继续查找删除
BST->Left = Delete(X,BST->Left);
else if(BST->Data < X) // X 比当前结点值大,在右子树继续查找删除
BST->Right = Delete(X,BST->Right);
else{ // 找到被删除结点
if(BST->Left && BST->Right){ // 被删除结点有俩孩子结点
tmp = FindMin(BST->Right); // 找到右子树中值最小的
BST->Data = tmp->Data; // 用找到的值覆盖当前结点
BST->Right = Delete(tmp->Data,BST->Right); // 把前面找到的右子树最小值结点删除
}else{ // 被删除结点只有一个孩子结点或没有孩子结点
tmp = BST;
if(!BST->Left && !BST->Right) // 没有孩子结点
BST = NULL;
else if(BST->Left && !BST->Right) // 只有左孩子结点
BST = BST->Left;
else if(!BST->Left && BST->Right) // 只有右孩子结点
BST = BST->Right;
free(tmp);
}
}
return BST;
}
// 中序遍历
void InOrderTraversal(BinTree BT){
if(BT){
InOrderTraversal(BT->Left); // 进入左子树
cout<<BT->Data; // 打印根
InOrderTraversal(BT->Right); // 进入右子树
}
}
int main(){
BinTree BST = NULL;
BST = Insert(5,BST);
BST = Insert(7,BST);
BST = Insert(3,BST);
BST = Insert(1,BST);
BST = Insert(2,BST);
BST = Insert(4,BST);
BST = Insert(6,BST);
BST = Insert(8,BST);
BST = Insert(9,BST);
/*
5
/\
3 7
/\ /\
1 4 6 8
\ \
2 9
*/
cout<<"中序遍历的结果是:";
InOrderTraversal(BST);
cout<<endl;
cout<<"查找最小值是:"<<FindMin(BST)->Data<<endl;
cout<<"查找最大值是:"<<FindMax(BST)->Data<<endl;
cout<<"查找值为3的结点左子树结点值为:"<<Find(3,BST)->Left->Data<<endl;
cout<<"查找值为7的结点右子树结点值为:"<<IterFind(7,BST)->Right->Data<<endl;
cout<<"删除值为5的结点"<<endl;
Delete(5,BST);
/*
6
/\
3 7
/\ \
1 4 8
\ \
2 9
*/
cout<<"中序遍历的结果是:";
InOrderTraversal(BST);
cout<<endl;
return 0;
}