MindSpore社区活动：基于MindSpore的SGD优化器实现

SGD，全称Stochastic Gradient Descent，随机梯度下降。核心思想是每次迭代时仅使用一个样本的梯度信息来更新模型参数。特别是在高维优化问题中，这减少了非常高的计算负担，实现更快的迭代以换取更低的收敛速度。随机梯度下降已成为机器学习中重要的优化方法。

梯度下降（Gradient Descent）

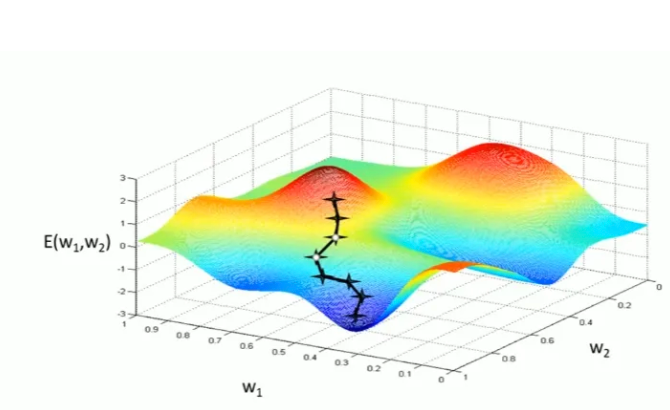
梯度下降是一种优化算法，用于最小化一个函数，通常在机器学习和人工智能中用于找到函数的局部最小值。这个函数通常是损失函数，它衡量了模型预测值与实际值之间的差异。梯度下降的核心思想是迭代地调整参数，以减少损失函数的值。用于求解无约束优化问题的迭代算法，特别常用于机器学习中的参数估计问题。其基本思想是，通过迭代地调整参数，沿着函数的负梯度方向寻找函数的局部最小值。

但是对于多维高次函数，梯度下降算法只能在局部找到最优解，但是不一定能找到全局最优解；并且传统的梯度下降很容易出现过拟合的情况。

随机梯度下降（SGD）

标准的梯度下降主要有两大缺点，一是训练过程及其缓慢，二是容易陷入局部最优解。

于是需要随机梯度下降算法。

在梯度下降的基础上，随机梯度下降从样本中随机抽出一组样本，训练后按梯度更新一次，然后再抽取一组样本更新一次。在样本量极其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型。

标准的随机梯度下降算法在每次参数更新时，仅仅选取一个样本计算梯度，用一个样本的梯度代替全部样本的梯度，能够大大加快训练速度。此外，由于每次迭代并不是都向着整体最优化方向，导致梯度下降的波动非常大，更容易从一个局部最优跳到另一个局部最优，但无法根本上解决局部最优问题。

我们通常所采用的SGD优化器，其实都采用Mini-batch Gradient Descent（小批量梯度下降法），我们熟悉的参数batch便应用于此。本质上是用一批样本的梯度代替全部样本的梯度。通常批大小选择2的倍数，方便计算机处理。

这种做好的好处是可以降低参数更新时的方差，收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。

SGD算法的几个问题

1.受抽取训练样本的影响较大。

2.没有解决梯度消失和梯度爆炸的情况。

3.无法处理过拟合的情况。

4.不能保证很好的收敛性。

基于MindSpore框架源码的SGD优化方法

MindSpore官方文档，SGD优化器的API

https://www.mindspore.cn/docs/zh-CN/r2.4.1/api_python/nn/mindspore.nn.SGD.html

MindSpore对SGD优化器已经使用了不少优化方法，有momentum,dampening,nesterov,weight-decay,gradients_centralization等。

动量法（Momentum）

原理

动量法在SGD的基础上引入了动量项，使得参数更新具有惯性。

优点

加速收敛：动量项使得参数更新具有惯性，能够更快地收敛到最优解。
减小震荡：动量项能够平滑梯度方向的变化，减小参数更新过程中的震荡。

缺点

需要调整额外的超参数：除了学习率之外，动量法还需要调整动量因子。

dampening

算法优点：当某个参数的梯度出现极端情况时，dampening算法能够削弱当前参数的梯度的值。从而减缓梯度对真实参数的影响，主要是作用于梯度爆炸时的情况。

nesterov

属于momentum算法的变种，与momentum唯一区别就是：计算梯度的不同。nesterov动量中，先用当前的速度vi临时更新一遍参数，再用更新的临时参数计算梯度。因此，nesterov动量可以解释为在momentum动量方法中添加了一个校正因子。

weight-decay

为了防止过拟合问题的出现，可以使用权值衰减做进一步的优化。增加了权值衰减项后，当计算过程中出现过拟合的情况下可以根据当前情况使用weight-decay Optimizer消除过拟合现象。在当前华为MindSpore框架中，在参数未分组时，优化器配置的 weight_decay 应用于名称不含“beta”或“gamma”的网络参数；参数分组情况下，可以分组调整权重衰减策略。

decay_weight函数首先调用get_weight_decay函数获取当前权重衰减的值，接着判断当前参数是否分组，若已经分组，则可以将weight_decay（权重衰减值）应用在所有网络中，即应用在所有数据集后续训练中；若已经分组，则要选择应用在指定的网络中（名称不含“beta”或“gamma”的网络），返回新的梯度。

get_weight_decay函数返回的是当前权重衰减的值，首先判断当前权重衰减值是否动态变化，若变化且当前数据向量已经分组，则循环将权重衰减值加上当前一轮迭代的权重衰减值，知道当前的权重衰减值不在总体训练集的衰减范围内，返回衰减值；若当前数据向量还未分组，则直接返回当前一轮迭代的权重衰减值；若当前权重衰减值已经不变（即已经收敛到最低点），则直接返回权重衰减值。

算法优点：在公式后边加上可训练的weight_decay参数，可以有效防止过拟合现象的出现。

Gradient Centralization（梯度中心化）

Gradient Centralization的思想由论文: Gradient Centralization: A New Optimization Technique for Deep Neural Networks提出，号称一行代码就能加速训练并提升准确率。Gradient Centralization的做法很简单：直接对梯度向量进行零均值化。Gradient Centralization能够加速网络训练，使网络的训练更加稳定，提高网络的泛化能力，并且能够轻松地嵌入各种优化器中。

SGD应用案例

本案例使用数据集Fashion MNIST训练lenet网络模型，中间调用MindSpore提供的SGD优化器API，并设置三组实验来对比SGD优化器不同参数的选择对模型训练带来的影响。三组实验学习率固定设为0.01。实验一为SGD不带任何优化参数，实验二为SGD+momentum，实验三为SGD+momentum+nesterov。momentum与nesterov在理论上都能加速网络训练。最后通过实验数据可视化分析，得出结论。

数据集

Fashion MNIST（服饰数据集）是经典MNIST数据集的简易替换，MNIST数据集包含手写数字（阿拉伯数字）的图像，两者图像格式及大小都相同。Fashion MNIST比常规 MNIST手写数据将更具挑战性。两者数据集都较小，主要适用于初学者学习或验证某个算法可否正常运行。他们是测试和调试代码的良好起点。

Fashion MNIST/服饰数据集包含70000张灰度图像，其中包含60,000个示例的训练集和10,000个示例的测试集，每个示例都是一个28x28灰度图像。

网络模型

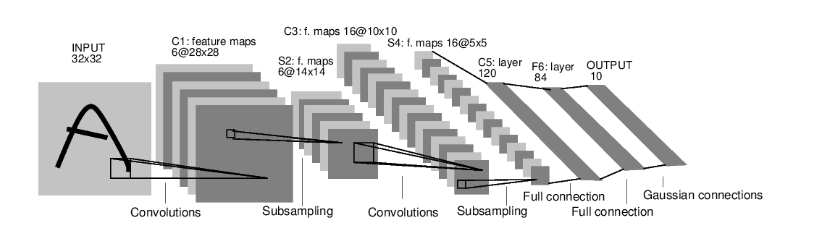
LeNet是卷积神经网络的开山之作，也是将深度学习推向繁荣的一座里程碑。LeNet是一个 7 层的神经网络，包含 3 个卷积层，2 个池化层，1 个全连接层。其中所有卷积层的所有卷积核都为 5x5，步长 strid=1，池化方法都为全局 pooling，激活函数为 Sigmoid，网络结构如下：

由于数据集比较简单，使用更为复杂的网络模型训练很快就能收敛，很难体现出优化器选择带来的影响。所以，我们选择LeNet。

实验步骤

首先配置环境，要求MindSpore>=1.8.1,还需要安装mindvision和解决兼容性问题。另外图像处理还需要安装opencv

由于mindvision支持几种经典数据集，其中就有FashionMnist。我们直接使用mindvision接口下载FashionMnist数据集，并且无需进行数据预处理。

from mindspore import ops
from mindspore import nn
import csv

from mindvision.classification.dataset import FashionMnist

download_train = FashionMnist(path="./FashionMnist", split="train", batch_size=32, repeat_num=1, shuffle=True,
                         resize=32, download=True)

download_test = FashionMnist(path="./FashionMnist", split="test", batch_size=32, resize=32, download=True)

train_dataset = download_train.run()
test_dataset = download_test.run()复制

检查数据集结构

for image, label in train_dataset.create_tuple_iterator():
    print(f"Shape of image [N, C, H, W]: {image.shape} {image.dtype}")
    print(f"Shape of label: {label.shape} {label.dtype}")
    break复制

使用LeNet网络，因为这是一个优化器算法比较案例，对网络没有特殊要求，这里推荐直接使用mindvision提供的接口。记得数据集为灰度图，通道数需要设为1。

from mindvision.classification.models import lenet

network = lenet(num_classes=10, num_channel=1, include_top=True)复制

创建训练函数和测试函数。对于测试函数，采用两个指标来评估模型质量：一是在测试集上的预测精度，二是在测试集上的平均损失。将这两个数据保存在csv文件中，方便后续处理。

from mindspore import ops
from mindspore import nn
# 定义训练函数
def train(model, dataset, loss_fn, optimizer):
    # Define forward function
    def forward_fn(data, label):
        logits = model(data)
        loss = loss_fn(logits, label)
        return loss, logits

    # Get gradient function
    grad_fn = ops.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=True)

    # Define function of one-step training
    def train_step(data, label):
        (loss, _), grads = grad_fn(data, label)
        loss = ops.depend(loss, optimizer(grads))
        return loss

    size = dataset.get_dataset_size()
    model.set_train()
    for batch, (data, label) in enumerate(dataset.create_tuple_iterator()):
        loss = train_step(data, label)

        if batch % 100 == 0:
            loss, current = loss.asnumpy(), batch
            print(f"loss: {loss:>7f}  [{current:>3d}/{size:>3d}]")


# 除训练外，我们定义测试函数，用来评估模型的性能。

def test(model, dataset, loss_fn, writer):
    num_batches = dataset.get_dataset_size()
    model.set_train(False)
    total, test_loss, correct = 0, 0, 0
    for data, label in dataset.create_tuple_iterator():
        pred = model(data)
        total += len(data)
        test_loss += loss_fn(pred, label).asnumpy()
        correct += (pred.argmax(1) == label).asnumpy().sum()
    test_loss /= num_batches
    correct /= total
    print(f"Test: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
    correct = round(correct * 100, 1)
    test_loss = round(test_loss,6)
    writer.writerow([correct, test_loss]) #将数据保存在对应的csv文件中复制

定义损失函数和优化器函数。损失函数使用交叉熵损失函数，优化器选择SGD，迭代次数为10，学习率固定设为0.01。在每次训练过后都将模型用测试集评估性能，来体现训练过程。

下面是实验一，使用纯粹的SGD优化器。

import csv
from mindvision.classification.models import lenet
from mindspore import nn
# 构建网络模型
network1 = lenet(num_classes=10, num_channel=1, include_top=True)

# 定义损失函数
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')

# 定义优化器函数
net_opt = nn.SGD(network1.trainable_params(), learning_rate=1e-2)
# 设置迭代次数
epochs = 10
csv_file1 = open('result/sgd1.csv', 'w', newline='') 
writer1 = csv.writer(csv_file1)
writer1.writerow(['Accuracy', 'Avg_loss'])
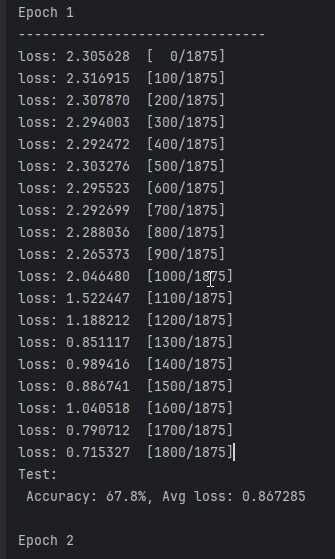
for t in range(epochs):
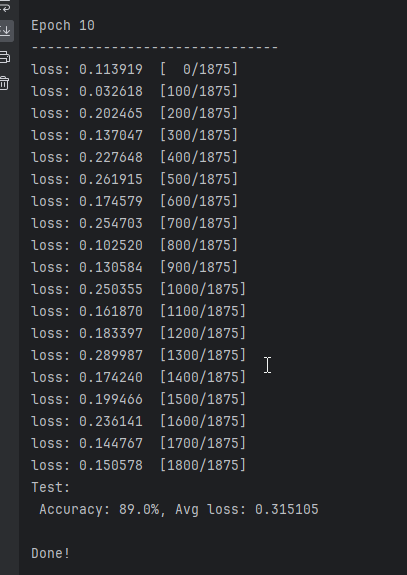
    print(f"Epoch {t+1}\n-------------------------------")
    train(network1, train_dataset, net_loss, net_opt)
    test(network1, test_dataset, net_loss, writer1)
csv_file1.close()
print("Done!")复制

实验二，控制其它变量不变，选择SGD优化器并使用参数momentum,设为0.9

import csv
from mindvision.classification.models import lenet
from mindspore import nn

network2 = lenet(num_classes=10, num_channel=1, include_top=True)
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')

# 定义优化器函数
net_opt = nn.SGD(network2.trainable_params(), learning_rate=1e-2, momentum=0.9)
epochs = 10
csv_file2 = open('result/sgd2.csv', 'w', newline='')
writer2 = csv.writer(csv_file2)
writer2.writerow(['Accuracy', 'Avg_loss'])
for t in range(epochs):
    print(f"Epoch {t+1}\n-------------------------------")
    train(network2, train_dataset, net_loss, net_opt)
    test(network2, test_dataset, net_loss, writer2)
csv_file2.close()
print("Done!")复制

实验三，控制其它变量不变，选择SGD优化器并使用参数momentum,设为0.9，使用参数nesterov，设置为True

import csv
from mindvision.classification.models import lenet
from mindspore import nn

network3 = lenet(num_classes=10, num_channel=1, include_top=True)
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')

# 定义优化器函数
net_opt = nn.SGD(network3.trainable_params(), learning_rate=1e-2, momentum=0.9, nesterov=True)
epochs = 10
csv_file3 = open('result/sgd3.csv', 'w', newline='')
writer3 = csv.writer(csv_file3)
writer3.writerow(['Accuracy', 'Avg_loss'])
for t in range(epochs):
    print(f"Epoch {t+1}\n-------------------------------")
    train(network3, train_dataset, net_loss, net_opt)
    test(network3, test_dataset, net_loss, writer3)
csv_file3.close()
print("Done!")复制

可视化分析

到此为止，我们获得了实验所有的数据，现在使用matplotlib对数据进行可视化分析。

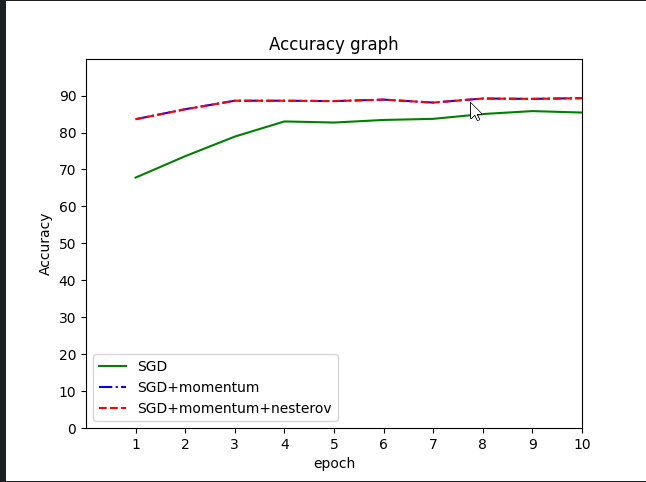
首先对预测精度相关数据进行绘图

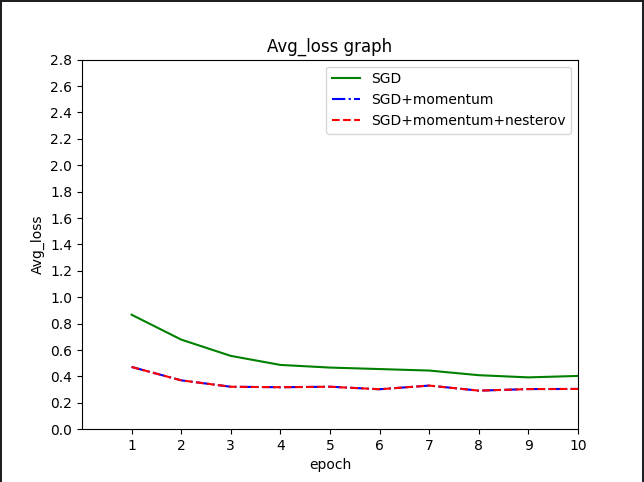
对平均损失相关数据进行绘图

结果分析

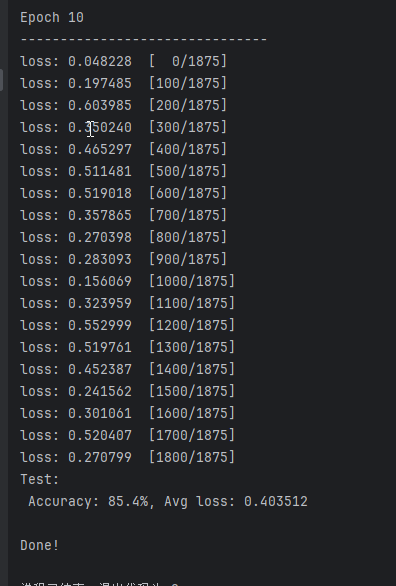
无论是预测精度还是平均损失，纯粹的SGD表现并不是很好。第一个epoch之后，SGD预测精度只有67%随着迭代次数增加，SGD的预测精度才慢慢增加，平均损失逐渐下降。10个epoch之后，SGD预测精度才不到85%。根据额外的实验，大概20个epoch能收敛到88%左右，这也是用fashion-minist数据集训练lenet所能达到的最高精度。

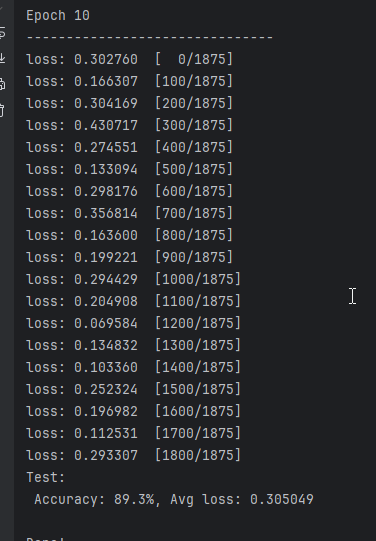
而使用momentum优化后，算法性能得到了质的飞跃，大概3个epoch就能收敛。

理论上来说，nesterov算法可以有效加速网络训练并减少波动。由于本实验所采用的数据集和网络模型都比较简单，算法优势没能很好的体现出来。

由上述实验，我们可以得到的结论是，选择SGD优化器，momentum参数是非常有用的。

目前，最流行并且使用很高的优化器包括SGD、RMSprop、AdaDelta和Adam。每种优化器都有不同参数需要调试。在实际应用中，选择哪种优化器应结合具体问题。在充分理解数据的基础上，依然需要根据数据特性、算法特性进行充分的调参实验，找到最优解。