问题
1 选题介绍
当前,卫星移动通信、气象预报、遥感探测、军事侦察、资源勘探、灾害监测、导航定位等多个领域发挥着越来越重要的作用。而且,在一般的航天任务应用中,我们往往需要使用一群卫星共同来完成任务。将一群卫星的集合,称作卫星星座。
在每个时刻,卫星的服务范围可以近似成一个锥形的区域。该锥形区域在地面上的投影为圆形的。如果该时刻,地面目标在该圆形区域内,则卫星可以对该地面目标提供服务,称作“地面目标在该时刻被卫星覆盖”。
卫星对一个地面目标的时间窗口,是指在仿真时间内,卫星对目标可以提供服务的时间段的集合。时间窗口可以表示为一个时间区间,在该区间内卫星能够对目标提供服务,而不在该时间区间内,卫星不能对目标提供服务。
卫星星座对一个地面目标的时间窗口,为星座中每颗卫星对目标时间窗口的并集。
对于一个区域,我们想知道在一个时间段内,卫星星座对它可见的范围有多少。我们常使用覆盖率这一指标。所谓卫星对区域的覆盖率,等于被覆盖的面积与区域总面积之比。
然而,要直接计算区域目标被卫星群覆盖的面积是较为困难的,因为需要将区域与球面圆相交求相交面积。因此,为了计算星座对区域的覆盖率,我们可以将区域目标划分为若干个小的网格,通过计算每个网格是否被卫星覆盖,从而得到覆盖率的计算结果。
2 选题分析
2.1问题分析
2.1.1 计算对应城市时间窗口及其最值,累计值
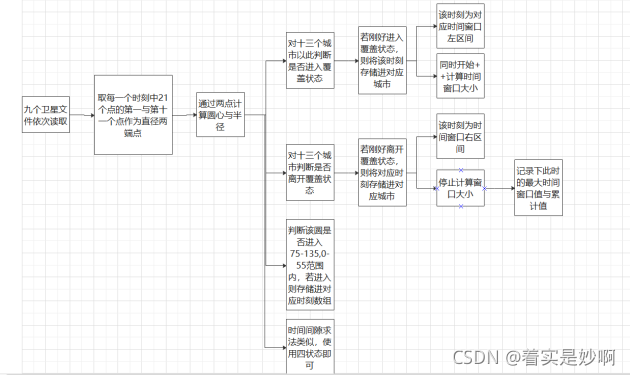
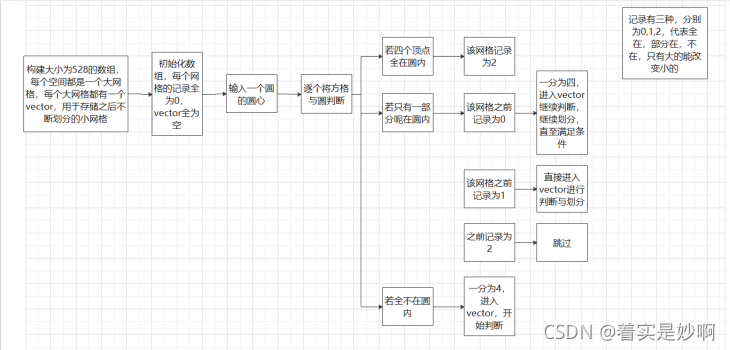
时间窗口:对于该问题而言,我们已知有九个卫星正在地球上方处于运动状态,并且每个卫星在每一秒下所覆盖的区域也已经使用对其边界进行打点的方法,对每一秒的对应边界打下了二十一个点,存储于对应的九个文件中,所以,期初我认为我们第一步要做的是依次将九个文件下从第零秒到第86400秒对应的多边形与十三个城市依次通过城市的点与多边形的某一点形成的直线与多边形相交的点数进行判断,判断出该城市此刻是否处于卫星笼罩下,并记录下对应时间形成时间窗口,但是该方法会出现一个较大的问题在于虽然求出的各个时间窗口的窗口大小比较精准,但是计算时间过于漫长,每运行一次大概需要五到六分钟,不利于我们之后进行其他题目的计算与分析矫正,于是,我通过观察发现各个卫星的笼罩区域类似于一个圆形,并且,在每一个圆形取得的二十一个边界点中,第一个边界点与第十一个边界点分别都处于对应二十一个点中的最高位置与最低位置,于是我们可以将这两个点视为对应圆的直径的两个端点,以此来计算对应圆的圆心以及半径,计算得到圆心后使用 (x-x1)2-(y-y1)2与R2判断,得到对应城市在该秒是否刚好处于圆中,若是,则记录下对应的时间,作为该时间窗口的区间左值;若该城市刚好出圆,则记录下对应时间,作为该时间窗口的区间右值,然后再继续循环,不断寻找时间窗口。寻找时间窗口对应步骤如下:
1.依次打开九个卫星对应的txt文件,取出每一秒下对应圆的二十一个点中的第一个点与第十一个点。(需要注意,我们只取第一和第十一,其余点全部跳过)
2.将这两个点作为直径两端点,取中心得到该圆圆心,计算距离得到半径,将球坐标转换为之间坐标
3.将该圆与十三个城市对应的直角坐标进行比对计算,使用 (x-x1)2-(y-y1)2与R2判断,当城市刚进入圆内以及刚从圆内出来时,分别记录下两个时刻,作为该时间窗口的左区间值及右区间值
4.不断重复上述步骤,当一个文件的86400秒计算完毕后,打开下一个文件,继续重复。
最值及累计值:该问题的求解只需要在上述问题的前提下,当城市刚好进入圆时,进行变量的++计算;当城市刚好从圆中出来时,停止++计算并且将此时++计算得到的值,与之前的历史最优解进行比较,若该变量值大于(小于)历史最优解,就替代他,求得最大值(求得最小值),并且将每个时间窗口++得到的值都累积起来,就得到了该城市的累计值。步骤如下:
1.在取得圆心之后,依次与十三个城市进行比较时,若该城市刚好进入圆中,对变量开始进行++计算
2.当城市刚好从圆中出来时,停止++计算,并且将++后的值累计起来,再将该++后的值与之前的历史最优解进行比较,得到此时的最大值与最小值
3.不断循环,最终得到最值与累计值。
时间间隙及其最值累计值:该问题的求解与求解时间窗口以及时间窗口的累计值和最值有异曲同工之妙,该处我同样是选择当圆上一秒不在圆中,而此刻处于圆中时作为时间间隙左值;上一秒处于圆外,而下一秒处于圆中作为时间间隙右值,而最大值,最小值,累计值的计算都与时间窗口相同。
图一.第一小题流程
2.1.2 求解范围内时间间隙最大值最小点坐标及平方和最小点坐标
该问题的求解从具体的题目含义中脱离出来后发现,其实还是一种在给定范围内求解最优解的问题,而解决该类最优解问题常用的方法有诸如遗传算法,粒子群算法等比较好的模拟算法,而粒子群算法相对于遗传算法而言收敛更快,并且比一遗传算法更加成熟,于是对
于该问题的求解我选择使用粒子群算法。
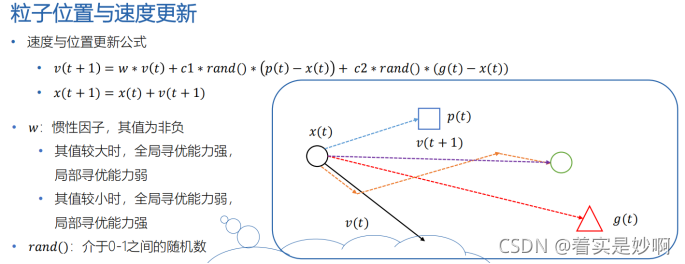
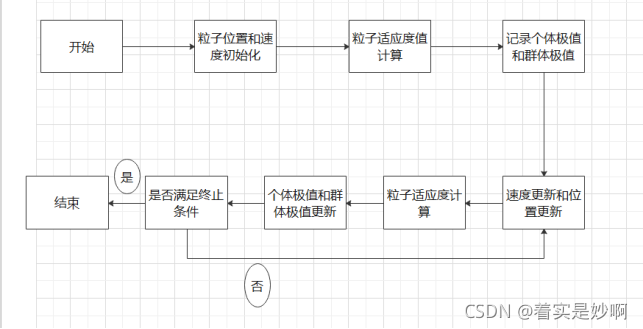
粒子群算法说明:粒子群算法主要是通过建立一个鸟的种群,该种群中的每一只鸟都有自己的初始位置以及速度矢量,每一只鸟儿都知道自己曾经走过的所有位置中的最优解(局部最优)以及整个种群在目前代数下得到过的最优解(全局最优),每一只鸟儿再进行下一次迭代时都会改变自身的位置,而自身位置向何处变化不仅取决于自己当前所处的位置,更取决于自身速度矢量,自身局部最优解矢量以及全局最优解矢量,在这四者的共同影响下,鸟儿才做出行走决策。为什么要取决于自身最优解,自身速度矢量以及全局最优矢量?因为鸟儿会朝着对自身更优的方向前进,而模拟算法就是去模拟鸟儿的行为规律,每一只鸟儿都会想着,自己之前找到过一个对我而言最好的地方,我是不是应该再往那边靠靠?我的种群找到过一个更好的地方,我是否也应该往那边去看看,所以在综合了这几个量之后,得到了我们粒子群算法的核心公式,也即每只鸟儿在进行每次迭代时的前进公式,如下图:
图二.粒子群图
其中v(t+1)就是鸟儿在进行完本次迭代之后所拥有的速度,而速度加上鸟儿所在位置就得到本次迭代之后的鸟儿位置。而p(t)与g(t)分别代表了局部最优解以及全局最优解。
粒子群构造:我选择使用数量为5的种群,由于是要求解75-135,0-55范围内的时间间隙最小点坐标,而通过上一道题的计算能够发现圆的半径基本都在7.0063左右,于是我们可以在第一题时就将处于67.9932-142.0068,以及-7.0068-62.0068的范围内的圆心对应于每一秒将其存储下来,具体的思路为构造一个86400大小的数组,每一个空间内部都对应一个vector容器用于存储圆心;当求出圆心后就判断该圆心是否处于上述范围,如果处于,就将该圆心存储到该圆对应的时刻之下,最终数组构造完成。在得到了每一秒能经过的圆心数组时,我们就可以开始适应函数的制作。
适应函数制作:该适应函数类似于第一题中求解时间间隙,具体为函数先得到要求的鸟儿此时所处的位置,然后将该位置在86400的数组里进行循环遍历,寻找何时该位置处于圆内或者处于圆外,在此处我使用了四种状态来对应此位置可能出现的情况,分别为:00代表此刻处于时间间隙;01代表前一秒处于时间窗口,此时进入时间间隙;10代表前一秒处于时间间隙,此时处于时间窗口;11代表处于时间窗口内。当处于01状态时,启动++操作,并且在00状态下每一秒继续执行++操作;当进入10状态时,++操作停止,开始结算,以当前++后产生的结果与之前的时间间隙累计值进行比较,将最大值进行替换,86400次循环结束后,就得到了该位置下时间间隙的最大值。(时间间隙平方和最小点的适应函数类似,只是把每一个时间间隙的平方和都加起来,得到适应函数的输出)
局部最优与全局最优:在经过适应函数之后,鸟儿得到了其处于当前位置下的时间间隙最大值,将其与之前鸟儿所能得到的时间间隙最大值中的最小值(局部最优)进行比较,若
当前值更小,则将当前值替换为该鸟儿的局部最优,在该种群中所有鸟儿都在本次迭代中经过适应函数后,将所有鸟儿的本次时间间隙最大值与全局最优解进行比较,若有时间间隙最大值小于全局最优解,则进行替换。在迭代结束之后,种群中的全局最优就是我们想要的时间间隙最大值最小点。
具体过程如下:
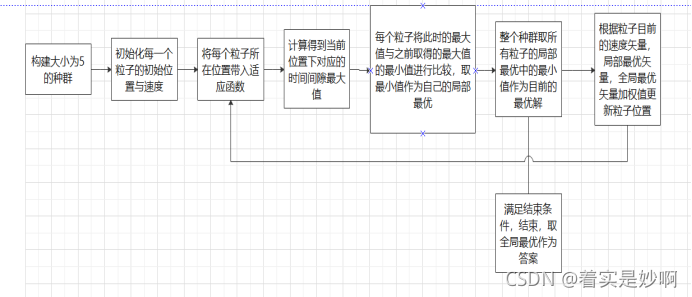
1.设置两个大小为五的种群,一个用于计算时间间隙最大值最小点,另一个用于计算时间间隙最大值平方和最小的点,每个种群都是一个数组,种群中每只鸟都会记录下自己当前所在的位置,当前的速度以及目前自己已经找到的最优解(局部最优)。
2.将种群中每只鸟都进行初始化,具体为在给定的范围,即67.9932-142.0068,以及-7.0068-62.0068的范围对鸟儿使用srand()函数进行随机赋值,给予它初始的位置,速度,并通过适应函数得到初始化的该鸟儿的局部最优解,初始化结束之后,通过比较所有的局部最优解得到全局最优解。
3.设置迭代次数,通过多次测试,我发现迭代二十次模型就已经成熟。在每一次迭代时都要通过粒子群公式Vi+1=Vi+c1rand()(pbest-xi)+c2rand()(best-xi)得到每一只鸟儿新的速度以及新的位置,之后通过适应函数得到新的适应值,并借此来不断修改自己的局部最优解,以及整个种群的全局最优解,最终通过全局最优解得到整个问题的答案。
图三.粒子群流程
2.1.3 计算每个时刻覆盖率并绘制出曲线
对于从本小题开始之后的每一个题都用同一种思想即可解决——四叉树。在下一小题时,我会着重讲本程序的四叉树如何构造,而在此处我们默认四叉树已经构造完毕。
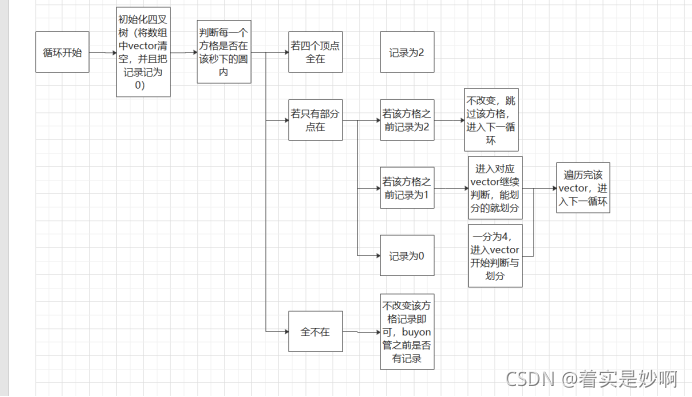
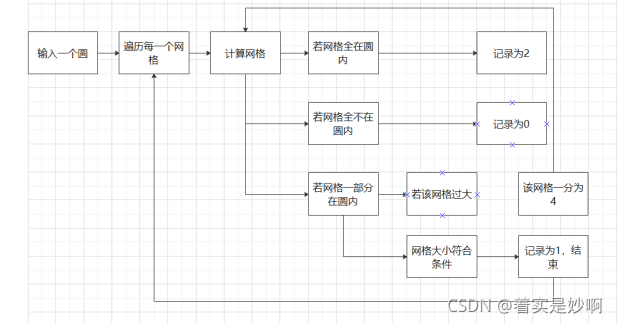
对于本小题而言,由于我的程序的四叉树使用数组构建,数组中的每一个空间都存储着一个网格,该网格可以不断一分为4,直至某一个网格边长小于等于0.625为止。本小题就从第0秒开始直至86399为止,不断循环,每次循环时都将四叉树进行初始化,然后用之前已经求出的86400下每一秒会经过该区域的圆的圆心数组对四叉树中的网格进行判断,若该网格的四个顶点全在圆中,则代表该网格彻底在圆中,记为2;若该网格的四个顶点全不在圆中,则代表该网格彻底不在圆中,记为0;若该网格只有一部分在圆中,并且该网格边长大于0.625,则将该网格置为1,并将该网格一分为四,对四个小网格进行相同的判断,直至网格被记为0,2或边长小于等于0.625为止,并将最终还是只有一部分处于圆内的小网格标记为1。具体步骤如下:
1.从第零秒开始,取出对应秒数下会出现的圆心,初始化四叉树判断四叉树中的网格是否完全处于圆内,若是,则记录为2;若完全不处于圆内,记录为0;
若只有一部分处于圆内,记录为1,并且若该网格边长大于0.625,则一分为四,继续同样的判断,当小于等于0.625时,不再细分。
2.当该一秒的所有圆对四叉树遍历完毕后,通过计算四叉树中所有被记录为2的网格的面积得到该秒下的覆盖面积,除以总面积,得到该秒的覆盖率,将覆盖率存储下来,继续循环,最终绘制曲线即可。
图四.第三小题流程
2.1.4 绘制对应时刻下被覆盖网格及不确定网格
本题的解决方法主要在于需要先将对应的区域,即75-135,0-55这一块区域分成一个个网格,然后利用对应时刻下的圆心求解各个网格是否为全在圆内,全部在圆内以及部分在圆内,对于部分在圆内的网格就将其一分为四,并且重复上述判断,直到所有网格都被标记为0或2或1并且边长小于等于0.625为止。
四叉树构建:由于本题所要求解的区域为75-135,0-55,所以我选择将该矩形区域分解为528个小网格,边长为2.5,其中在程序画图中表现为行数为22,列数为24。这528个网格是一个大小为528的数组,该数组中每一个空间都存储着对应网格的左上角顶点坐标,网格边长,该网格的判断标志(0,1,2),以及一个vector容器,该vector容器用于当本空间对应的边长为2.5的网格需要一分为四时,将分出的四个小网格存储在vector中,而这四个小网格也是能够记录自己左上角顶点坐标,自己的边长以及自身标志(0,1,2),而这些小网格还需要细分时,细分后的网格尾加进入同一个vector中,并且把这个小网格删除出vector。对于网格在该圆进行判断前已经被之前的圆标记为2的,则不做计算,跳过;标记为0的,则继续计算;标记为1的,若该圆对其标记为2,则用2覆盖1,并将对应vector清空,若该圆对其标记为0,则不做计算,若该圆对其标记为1,则进入其vector进行同样判断。具体步骤如下:
1.构建大小为528的数组,代表将区域分为528个网格,每个网格内部都会记住自身左上角坐标,自身边长,以及自身此时是完全处于一个圆中(2),完全不处于一个圆中(0),部分处于一个圆中(1),每个边长为2.5的大网格还有一个vector容器,用于存储之后会划分的小网格,每个小网格同样会记住自身左上角坐标,自身边长,以及自身此时状态(0,1,2),但不包含vector容器,小网格的细分会尾加在对应大网格的vector中。
2.将界面中需要求解的时刻字符串转换为int类型,代入86400大小的圆心数组中,得到对应时刻下出现在该区域中的圆,依次将每个圆与所有大网格进行判断,将大网格标记为0,1,2;若为1时,将大网格进行划分,一分为4个小网格,存入vector,再用该圆与vector中小网格进行判断,标记为0,1,2,;若为1,则将对应小网格一分为四,尾加进入vector,并将给小网格删除,继续判断,直至所有小网格全标记为0,2或者标记为1,但边长已经小于等于0.625,结束对本大网格的判断,进入下一大网格。
3.不断遍历,最终得到所有网格的标记
4.若同一时刻下有多个圆出现时,第一个圆之后的每一个圆在计算大网格前会先判断大网格是否已被记录为2,若是,则跳过该网格,若不是,则进行相同计算;若大网格之前为1,此时为2,则将对应vector清空;若大网格之前为1,此时仍然为1,则进入其vector进行状态判断。
5.对于需要细分的小网格,一分为四后需要将原网格删除
6.该秒计算完毕之后,遍历四叉树中所有网格以及vector,若大网格被标记为2,则为红色;被标记为0,不上色;被标记为1,进入vector容器中,对小网格进行上色。完毕之后,将四叉树初始化。
图四.第四小题流程
2.1.5 计算前一二三小时对应覆盖率
由于上一题中已经得到每一秒覆盖区域的计算方法,此时只需要在保留每一秒对所有网格的状态改变下,进行前3600秒,7200秒,10800秒的判断即可。需注意在上一题中所说的,若网格在该圆判断之前已经拥有了状态,那只有大状态可以改变小状态,即2状态可以改变1,0状态;1状态可以改变0状态,反之都不可。当原有状态为1,而该圆判断状态也为1时,进入vector中再判断各小网格是否在圆中。最终得到所有的覆盖面积,也就可以算出对应覆盖率。
2.1.6 将上述覆盖区域,不确定区域进行绘制
同样的,上一题已经在每一秒不重新初始化四叉树的情况下得到了前3600秒或7200秒或10800秒的整个四叉树的状态,由于求取的秒数太多,四叉树中可能出现虽然大网格被记录为1,但是其对应的vector容器中的小网格却全被记录为2,,所以为了消除这种情况,在计算完各时段的四叉树后,我们要便利一次四叉树,将四叉树中所有出现上述情况的大网格全被记录为2,并且清空其vector,这样做的好处在于之后对网格进行绘制时,应该整个被覆盖为红色的大网格就不会被分成许多小网格,影响美观。
2.2输入与输出分析
第一小题:输入为九个卫星文件,取得每一个卫星对应每一秒的圆心与半径。输出为对应十三个城市的时间窗口,时间间隙,以及两者对应的最大值,累计值。
第二小题:无输入,输出为对应区域内时间间隙最大值最小点坐标以及时间间隙最大值的平方和最小的点的坐标。
第三小题:无输入,输出为一天时间,即86400秒下,每一秒对应的覆盖率所绘制出的曲线
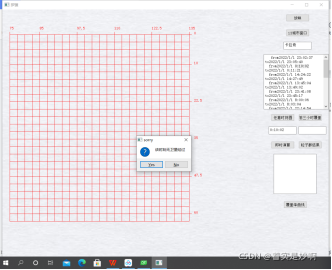
第四小题:输入为任意一个时刻,输入方式为比如13:05:01,系统将其转换为对应的秒数。输出为画出对应秒数下区域内被覆盖的网格以及不确定的网格。
第五小题:输入为1或2或3。输出为对应三个时段的累计覆盖率。
第六小题:输入为1或2或3.输出为对应三个时段所表示出的被覆盖网格及不确定网格。
2.3问题难点分析
本程序的难点主要在于:
1.如何将九个卫星文件中每一秒对应的多边形读出,将其与十三个城市进行判断,并且最重要的是速度不能太慢,若速度太慢会影响之后没一个问题的设计,并且对于每一次程序的运行都是一种巨大的累赘。解决方法为将多边形置换为圆,并且只取每一秒下第一个点与第十一个点来计算对应圆心与半径,这样就能大大加快程序的运行速度。
2.如何去寻找区域内时间间隙最大值最小点坐标以及时间间隙平方和最小点坐标。解决方法为使用粒子群算法,让每一个粒子在不断的迭代中取寻找最小点坐标。
如何计算被覆盖网格以及不确定网格,并且不确定网格不能过大。解决方法为使用四叉树的思想,若一个格子被判断为四个顶点皆在圆内,则被画为红色,若一个格子被判定为不确定,则被一分为四,继续判断,直至网格到达规定界限,不能再细分为止。
算法设计
3.1数据结构设计
1.设计一个86400大小的数组,数组中每一个空间都代表了对应秒数下会出现圆的圆心,便于之后使用四状态求出时间间隙
2.设计另一个86400大小的数组,该数组同样也是存储对应秒数下会出现的圆的圆心,但这些圆必须是能笼罩75-135以及0-55这片区域的,用于之后适应函数的使用。
3.设计一个528大小的数组,该数组就代表了四叉树,528代表了有528个格子,横行22,纵列24,其中的每一个空间装载了对应格子的左上角坐标以及对应边长,标志,用于存放小网格的vector。
4.设计一个大小为13的数组,用于存放13个城市的名字以及对应的直角坐标
5.设计大小为5的种群数组,其中的每一个空间都是一只鸟,装载了对应鸟儿此时所处的位置,速度以及自己已经找到过得最优解。
3.2算法思想
本程序的设计主要使用了模拟算法的思想,比如粒子群算法(也称粒子群优化算法或鸟群觅食算法),粒子群算法模仿昆虫、兽群、鸟群和鱼群等的群集行为,利用群体中的个体
对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得最优解,粒子群优化算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。
四叉树算法思想主要为首先将把一副图像或栅格地图等分成四个一级字块,顺序为左上,右上,左下,右下;然后逐块检查其中所有格网状态是否满足,若满足,则该字块不再分;若不满足,则将该子块进一步分成四个二级子块;如此递归地分割,直到每个子块的状态满足为止。
3.3算法设计
本程序的制作主要使用了两个算法,粒子群算法与四叉树
粒子群算法设计:设计一个大小为5的种群,其中每一个粒子都有独立的状态,包括目前所处的位置,目前的速度,以及自己曾经找到过的最优解。对于整个种群而言,每一个粒子都知道整个种群目前出现过的最好解。每一个粒子都会受自己和整个种群的影响来改变自己的位置和速度,不断寻找更好的解,最终得到最优解。
图五.粒子群算法流程
四叉树:设计一个数组来代表每一个网格,当一个网格满足需要划分的条件时,将该网
格一分为四,进行同样的判断,一旦满足,就对该小网格进行划分,直至网格满足条件后结束划分。
图六.四叉树流程
3.4核心算法详解
粒子群算法详解:粒子群优化算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解,而对于本题来说最优解就是时间间隙最大值最小点的坐标,所以在设计适应函数时,适应函数的输入就为一个坐标,而适应函数就通过这个坐标进行计算,输出这个坐标对应的时间间隙的最大值。粒子群中的每一个粒子就通过判断自己此时与过往所处坐标的时间间隙最大值,取最小的一个来作为自己曾经找到的最优解,在所有粒子都找到了目前对于自己而言的最优后,整个种群就选取最小的来作为目前整个种群所找到的最优。然后每个粒子就基于当前的位置,通过受自己已有速度矢量,局部最优解矢量,全局最优解矢量的加权影响下,改变速度与位置,继续寻找更好的坐标点,在循环结束后,取全局最优来作为整个题目的答案即可。具体过程如下:
1.设置两个大小为五的种群,一个用于计算时间间隙最大值最小点,另一个用于计算时间间隙最大值平方和最小的点,每个种群都是一个数组,种群中每只鸟都会记录下自己当前所在的位置,当前的速度以及目前自己已经找到的最优解(局部最优)。
2.将种群中每只鸟都进行初始化,具体为在给定的范围,即67.9932-142.0068,以及-7.0068-62.0068的范围对鸟儿使用srand()函数进行随机赋值,给予它初始的位置,速度,并通过适应函数得到初始化的该鸟儿的局部最优解,初始化结束之后,通过比较所有的局部最优解得到全局最优解。
设置迭代次数,通过多次测试,我发现迭代二十次模型就已经成熟。在每一次迭代时都要通过粒子群公式Vi+1=Vi+c1rand()(pbest-xi)+c2rand()(best-xi)得到每一只鸟儿新的速度以及新的位置,之后通过适应函数得到新的适应值,并借此来不断修改自己的局部最优解,以及整个种群的全局最优解,最终通过全局最优解得到整个问题的答案。
四叉树详解:本程序使用四叉树主要是为了在碰到一个网格并非完全在圆内时,将这个过大的网格一分为四,再对每一个小网格进行判断,并且对于依旧有一部分不在圆内的网格继续划分,直至这种类型的网格足够小为止。
具体步骤如下:
1.构建大小为528的数组,代表将区域分为528个网格,每个网格内部都会记住自身左
上角坐标,自身边长,以及自身此时是完全处于一个圆中(2),完全不处于一个圆中(0),部分处于一个圆中(1),每个边长为2.5的大网格还有一个vector容器,用于存储之后会划分的小网格,每个小网格同样会记住自身左上角坐标,自身边长,以及自身此时状态(0,1,2),但不包含vector容器,小网格的细分会尾加在对应大网格的vector中。
2.将界面中需要求解的时刻字符串转换为int类型,代入86400大小的圆心数组中,得到对应时刻下出现在该区域中的圆,依次将每个圆与所有大网格进行判断,将大网格标记为0,1,2;若为1时,将大网格进行划分,一分为4个小网格,存入vector,再用该圆与vector中小网格进行判断,标记为0,1,2,;若为1,则将对应小网格一分为四,尾加进入vector,并将给小网格删除,继续判断,直至所有小网格全标记为0,2或者标记为1,但边长已经小于等于0.625,结束对本大网格的判断,进入下一大网格。
3…不断遍历,最终得到所有网格的标记
4…若同一时刻下有多个圆出现时,第一个圆之后的每一个圆在计算大网格前会先判断大网格是否已被记录为2,若是,则跳过该网格,若不是,则进行相同计算;若大网格之前为1,此时为2,则将对应vector清空;若大网格之前为1,此时仍然为1,则进入其vector进行状态判断。
5.对于需要细分的小网格,一分为四后需要将原网格删除
该秒计算完毕之后,遍历四叉树中所有网格以及vector,若大网格被标记为2,则为红色;被标记为0,不上色;被标记为1,进入vector容器中,对小网格进行上色。完毕之后,将四叉树初始化。
4 运行图像
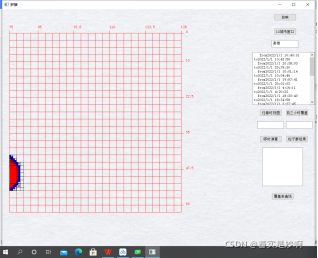
图七.实时放映经过的卫星
图八.任意时间窗口,间隙等
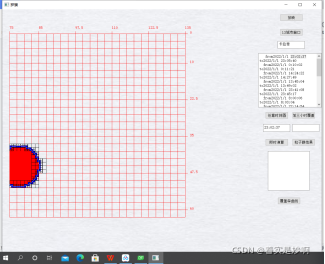
图九.任意时间的覆盖区域1
图十.任意时间的覆盖区域2
图十.粒子群
图十一.覆盖率曲线
代码(没有加数据文件,需要数据文件才能运行,而且还要把读取文件的地址改掉)
//cityname.h
#ifndef CITYNAME_H
#define CITYNAME_H
#include<QString>
struct city{
double jing;
double wei;
QString name;
city(){
jing=0,wei=0,name="";
}
};
class cityname
{
public:
cityname();
city team[13];
};
#endif // CITYNAME_H
//cityname.cpp
#include "cityname.h"
cityname::cityname()
{
team[0].jing=80.14;
team[0].wei=26.27;
team[0].name="坎普尔";
team[1].jing=265.67;
team[1].wei=39.02;
team[1].name="堪萨斯城";
team[2].jing=120.27;
team[2].wei=23.03;
team[2].name="高雄";
team[3].jing=67.02;
team[3].wei=24.51;
team[3].name="卡拉奇";
team[4].jing=85.19;
team[4].wei=27.42;
team[4].name="加德满都";
team[5].jing=23.54;
team[5].wei=54.54;
team[5].name="考纳斯";
team[6].jing=139.43;
team[6].wei=35.32;
team[6].name="川崎";
team[7].jing=49.1;
team[7].wei=55.45;
team[7].name="喀山";
team[8].jing=32.36;
team[8].wei=15.34;
team[8].name="喀士穆";
team[9].jing=102.5;
team[9].wei=16.25;
team[9].name="孔敬";
team[10].jing=89.34;
team[10].wei=22.49;
team[10].name="库尔纳";
team[11].jing=30.05;
team[11].wei=-1.59;
team[11].name="基加利";
team[12].jing=167.58;
team[12].wei=-29.03;
team[12].name="京斯顿";
}
//dialog.h
#ifndef DIALOG_H
#define DIALOG_H
#include <QDialog>
namespace Ui {
class Dialog;
}
class Dialog : public QDialog
{
Q_OBJECT
public:
explicit Dialog(QWidget *parent = nullptr);
~Dialog();
double shijian[86400];
double mm;
void paintEvent(QPaintEvent*);
private:
Ui::Dialog *ui;
};
#endif // DIALOG_H
//dialog.cpp
#include "dialog.h"
#include "ui_dialog.h"
#include"QPainter"
#include"QPen"
#include"QDebug"
Dialog::Dialog(QWidget *parent) :
QDialog(parent),
ui(new Ui::Dialog)
{
ui->setupUi(this);
}
Dialog::~Dialog()
{
delete ui;
}
void Dialog::paintEvent(QPaintEvent*){
QPainter painter(this);
QPen pen(Qt::red);
QPixmap map2(":/preview.jpg");
QRect q(0,0,1024,1024);
QRect q2(0,0,1800,800);
painter.drawPixmap(q2,map2,q);
painter.setPen(pen);
painter.drawLine(20,100,1728,100);
painter.drawLine(20,100,20,500);
painter.drawText(1728,90,"x/86400");
painter.drawText(20,510,"y/覆盖率");
painter.drawText(20,365,"15.15%");
double asda=0;
for(int i=1;i<86400;i++){
painter.drawLine(double(i-1)/50+20,shijian[i-1]/2+100,double(i)/50+20,shijian[i]/2+100);
if(asda<shijian[i])
asda=shijian[i];
}
qDebug()<<asda<<"asda";
}
下面是代码最主要部分
//mainwindow.h
#ifndef MAINWINDOW_H
#define MAINWINDOW_H
#include <QMainWindow>
#include<algorithm>
#include<cityname.h>
#include "secondque.h"
#include"QVector"
#include"dialog.h"
QT_BEGIN_NAMESPACE
namespace Ui { class MainWindow; }
QT_END_NAMESPACE
//对以下每个目标,计算星座对其时间窗口。同时,统计时间窗口的最大值、最小值与累积值。对每个目标,计算其时间间隙,并统计时间间隙的最大值与累积值
//在经度75°E-135°E,纬度范围0°N-55°N的区域范围内,寻找时间间隙最大值最小的点的坐标,以及时间间隙最大值的平方和最小的点的坐标,经纬度精确到0.1°
//计算每个时刻的瞬时覆盖率,并将结果绘制成曲线。
//(2)输入一个时刻(在仿真时段内),将该时刻区域内被覆盖的网格,不被覆盖的网格,不确定的网格用不同的颜色绘制出来
//计算前1小时,前2小时,前3小时的累积覆盖率
//(4)将三个时段区域内被覆盖的网格,不被覆盖的网格,不确定的网格用不同的颜色绘制出来。
struct shu{
int num[23];
shu(){
memset(num,0,sizeof (num));
}
};
//每个卫星用了21个数据来表示在某一时刻对应的圆
struct xing{
double x1;
double y1;
xing(){
x1=y1=0;
}
};
struct miao{
bool num[86400];
QString shijian;//用于存放在圆内的时间段
int jilu;//用于记录该城市是否是第一次进入圆中,以及何时出圆
int max,min,pingjun;//记录时间窗口最大最小和平均值
miao(){
for(int i=0;i<86400;i++)
num[i]=false;
shijian=" ";
jilu=-1;
max=pingjun=0;
min=1000000;
}
};
struct shike{
//用于存放86400秒中,每一秒能经过对应区域的圆心
QVector<xing>weixing;
};
struct gezi{//该结构体用于第三题时求解每个格子是否在圆内,用于画图
double x1,y1;//左上角
double temp;//边长
int flag;
gezi(){
x1=y1=temp=0;
flag=0;
}
};
struct gezi2{
double x1,y1,temp;//左上角,边长
int flag;
QVector<gezi>tem;
gezi2(){
flag=0;
temp=2.5;
}
};
class MainWindow : public QMainWindow
{
Q_OBJECT
public:
MainWindow(QWidget *parent = nullptr);
~MainWindow();
QString Wname[9]={"F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_0.txt","F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_1.txt","F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_2.txt","F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_3.txt","F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_4.txt","F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_5.txt","F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_6.txt","F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_7.txt","F:\\daerxiaQT\\WeiXingxitong\\SatCoverInfo_8.txt"};//文件路径数组
cityname cn;//装载各个城市名字,经纬度
shike lastxin[86400];//用于存储 在对应范围内 每秒出现的 卫星信息
shike alltime[86400]; //用于存储所有的卫星信息,计算时间间隙
gezi2 pack[528];
int eventid1,eventid2,id3,fangying;
void firque();
void lastque();
void qiujianxi();
void chushihua();
void tiaozheng(double x1,double y1,int&x2,int&y2);//减少网格计算量,寻找左上开始点与 右下结束点 x2,y2
int panduan(gezi&x,double x1,double y1);//判断小网格是否在园内
int panduan2(gezi2&x,double x1,double y1);// 大网格是否在园内
void huafen(double x1,double y1);// 大网格划分
void huafen2(gezi2& temp,double x1,double y1);//每个大网格中的 小网格进行划分
QString xinxi[13];//存储13个城市的时间窗口等各项信息
void paintEvent(QPaintEvent*);
void mousePressEvent(QMouseEvent*event);
void timerEvent(QTimerEvent *event);
int anniu;//按钮为0时, 不用画图, 为1时画图
int shu11;//用于最后一题中记录要求的 拟真时间
private:
Ui::MainWindow *ui;
Dialog*dialog;
};
#endif // MAINWINDOW_H
//mainwindow.cpp
#include "mainwindow.h"
#include "ui_mainwindow.h"
#include<cityname.h>
#include"QDebug"
#include"QFile"
#include"string"
#include"QString"
#include"QPainter"
#include"QPen"
#include"QMessageBox"
#include"QRectF"
#include"QMouseEvent"
#include"QBrush"
#include"cmath"
#include"QTimer"
//double 保留小数点后五位
//所有卫星都是不到两小时的周期(只是不到两小时转一圈而已)
MainWindow::MainWindow(QWidget *parent)
: QMainWindow(parent)
, ui(new Ui::MainWindow)
{
ui->setupUi(this);
eventid1=startTimer(2);
firque();
qiujianxi();
//tiaozheng(60,55,x2,y2);
chushihua();
id3=0;
fangying=0;
//就是在经度75-135内,纬度0-55内
int flag1=-1;
anniu=0;
connect(ui->pushButton,&QPushButton::clicked,[&](){
anniu=0;
flag1++;
if(flag1>=13)
flag1=0;
cityname zzz;
ui->textEdit->setText(xinxi[flag1]);
ui->textEdit_2->setText(zzz.team[flag1].name);
eventid2=0;
anniu=-1;
id3=0;
});
connect(ui->pushButton_2,&QPushButton::clicked,[&](){
for(int i=0;i<528;i++){
pack[i].flag=0;
pack[i].tem.clear();
}
anniu=1;
fangying=0;
QString read0;//输入拟真时间,到lastxin中查询该时间是否有圆经过区域,有则将该圆心存储
read0=ui->textEdit_3->toPlainText();
qDebug()<<read0;
QString st1="",st2="",st3="";
st1+=read0[0];
st1+=read0[1];
st2+=read0[3];
st2+=read0[4];
st3+=read0[6];
st3+=read0[7];
shu11=st1.toInt()*60*60+st2.toInt()*60+st3.toInt();
qDebug()<<st1<<st2<<st3<<shu11;
bool real=1;
if(lastxin[shu11].weixing.size()==0){
QMessageBox::question(this,"sorry","该时刻无卫星经过");
anniu=0;
real=0;
}
if(lastxin[shu11].weixing.size()!=0){
for(int i=0;i<lastxin[shu11].weixing.size();i++){
qDebug()<<lastxin[shu11].weixing[i].x1<<lastxin[shu11].weixing[i].y1;
huafen(lastxin[shu11].weixing[i].x1-75,lastxin[shu11].weixing[i].y1);
qDebug()<<"the end";
}
}
repaint();
});
connect(ui->pushButton_3,&QPushButton::clicked,[&](){
secondque aaa;
aaa.secque();
aaa.InitP();
for (int i = 0; i <20; i++) {
aaa.PT();
aaa.GT();
}
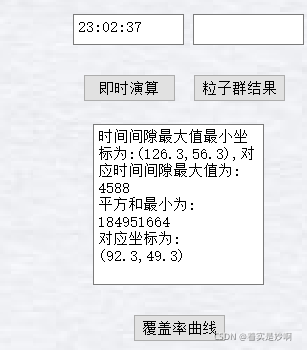
QString jianxi="时间间隙最大值最小坐标为:(";
//jianxi+=QString::number(aaa.min0.x.a1);
jianxi+="126.3,";
//jianxi+=QString::number(aaa.min0.x.a2);
jianxi+="56.3),对应时间间隙最大值为:";
//jianxi+=QString::number(aaa.min0.fit);
jianxi+="4588";
jianxi+='\n';
jianxi+="平方和最小为:";
//jianxi+=QString::number(aaa.pmin.fit2);
jianxi+="184951664";
jianxi+='\n';
jianxi+="对应坐标为:(92.3";
//jianxi+=QString::number(aaa.pmin.x.a1);
jianxi+=",";
//jianxi+=QString::number(aaa.pmin.x.a2);
jianxi+="49.3)";
ui->textEdit_4->setText(jianxi);
});
connect(ui->pushButton_4,&QPushButton::clicked,[&](){
for(int i=0;i<528;i++){
pack[i].flag=0;
pack[i].tem.clear();
}
double fugaiz=0;
QString read0;
read0=ui->textEdit_5->toPlainText();
int jshu=read0.toInt();
anniu=2;
fangying=0;
if(jshu==1){
for(int i=0;i<3600;i++){
for(int i1=0;i1<lastxin[i].weixing.size();i1++){
huafen(lastxin[i].weixing[i1].x1-75,lastxin[i].weixing[i1].y1);
}
}
bool jkl=0;
for(int i=0;i<528;i++){
if(pack[i].flag==1){
for(int i1=0;i1<pack[i].tem.size();i1++){
if(pack[i].tem[i1].flag==0||pack[i].tem[i1].flag==1)
jkl=1;
}
if(jkl==0&&pack[i].tem.size()!=0){
pack[i].tem.clear();
pack[i].flag=2;
}
}
}
for(int i=0;i<528;i++){
if(pack[i].flag==2){
fugaiz+=pack[i].temp*pack[i].temp;
}
else if(pack[i].flag==1){
for(int jk=0;jk<pack[i].tem.size();jk++){
fugaiz+=pack[i].tem[jk].temp*pack[i].tem[jk].temp;
}
}
}
repaint();
}
else if(jshu==2){
for(int i=0;i<7200;i++){
for(int i1=0;i1<lastxin[i].weixing.size();i1++){
huafen(lastxin[i].weixing[i1].x1-75,lastxin[i].weixing[i1].y1);
}
}
bool jkl=0;
for(int i=0;i<528;i++){
if(pack[i].flag==1){
for(int i1=0;i1<pack[i].tem.size();i1++){
if(pack[i].tem[i1].flag==0||pack[i].tem[i1].flag==1)
jkl=1;
}
if(jkl==0&&pack[i].tem.size()!=0){
pack[i].tem.clear();
pack[i].flag=2;
}
}
}
for(int i=0;i<528;i++){
if(pack[i].flag==2){
fugaiz+=pack[i].temp*pack[i].temp;
}
else if(pack[i].flag==1){
for(int jk=0;jk<pack[i].tem.size();jk++){
fugaiz+=pack[i].tem[jk].temp*pack[i].tem[jk].temp;
}
}
}
repaint();
}
else if(jshu==3){
for(int i=0;i<10800;i++){
for(int i1=0;i1<lastxin[i].weixing.size();i1++){
huafen(lastxin[i].weixing[i1].x1-75,lastxin[i].weixing[i1].y1);
}
}
bool jkl=0;
for(int i=0;i<528;i++){
if(pack[i].flag==1){
for(int i1=0;i1<pack[i].tem.size();i1++){
if(pack[i].tem[i1].flag==0||pack[i].tem[i1].flag==1)
jkl=1;
}
if(jkl==0&&pack[i].tem.size()!=0){
pack[i].tem.clear();
pack[i].flag=2;
}
}
}
for(int i=0;i<528;i++){
if(pack[i].flag==2){
fugaiz+=pack[i].temp*pack[i].temp;
}
else if(pack[i].flag==1){
for(int jk=0;jk<pack[i].tem.size();jk++){
fugaiz+=pack[i].tem[jk].temp*pack[i].tem[jk].temp;
}
}
}
repaint();
}
fugaiz/=3300;
ui->textEdit_5->setText(QString::number(fugaiz));
qDebug()<<"wancheng";
});
connect(ui->pushButton_5,&QPushButton::clicked,[&](){
dialog=new Dialog(this);
dialog->setModal(false);
dialog->setWindowTitle("罗骥图形");
for(int i=0;i<86400;i++){
dialog->shijian[i]=0;
}
int jj=-1;
for(int i=0;i<86400;i++){
for(int i=0;i<528;i++){
pack[i].flag=0;
pack[i].tem.clear();
}
if(1){
jj++;
for(int i1=0;i1<lastxin[i].weixing.size();i1++){
huafen(lastxin[i].weixing[i1].x1-75,lastxin[i].weixing[i1].y1);
}
for(int i2=0;i2<528;i2++){
if(pack[i2].flag==2){
dialog->shijian[jj]+=pack[i2].temp*pack[i2].temp;
}
else if(pack[i2].flag==1){
for(int jk=0;jk<pack[i2].tem.size();jk++){
dialog->shijian[jj]+=pack[i2].tem[jk].temp*pack[i2].tem[jk].temp;
}
}
}
}
}
qDebug()<<jj<<"jj";
dialog->show();
});
connect(ui->pushButton_6,&QPushButton::clicked,[&](){
fangying=1;
id3=0;
});
connect(ui->pushButton_7,&QPushButton::clicked,[&](){
QString jianxi="时间间隙最大值最小坐标为:(";
jianxi+="126.3,";
jianxi+="56.3),对应时间间隙最大值为:";
jianxi+="4588";
jianxi+='\n';
jianxi+="平方和最小为:";
jianxi+="184951664";
jianxi+='\n';
jianxi+="对应坐标为:(92.3";
jianxi+=",";
jianxi+="49.3)";
ui->textEdit_4->setText(jianxi);
});
}
MainWindow::~MainWindow()
{
delete ui;
}
//经度75-135内,纬度0-55内
void MainWindow::paintEvent(QPaintEvent*){
QPainter painter(this);
QPen pen(QColor(255,0,0));
painter.setPen(pen);
QPixmap map2(":/2.jpg");
QRect q(0,0,500,500);
QRect q2(0,0,1400,1200);
painter.drawPixmap(q2,map2,q);
//画图从400画到900差不多,就是在经度75-135内,纬度0-55内
for(int i=1;i<=25;i++){
if(i%5==0||i==1){
painter.drawLine(i*30,90,i*30,850);//画经度线
double bv=72.5+i*2.5;
QString bvn=QString::number(bv);
painter.drawText(i*30,80,bvn);
}
else
painter.drawLine(i*30,100,i*30,850);
if(i%5==0||i==1){
painter.drawLine(30,100+(i-1)*30,760,100+(i-1)*30);//画纬度线
double bv=-2.5+i*2.5;
QString bvn=QString::number(bv);
painter.drawText(770,100+(i-1)*30,bvn);
}
else
painter.drawLine(30,100+(i-1)*30,750,100+(i-1)*30);
}
painter.drawLine(30,850,750,850);
if(anniu==1&&lastxin[shu11].weixing.size()){//12:31:17,126格
for(int i=0;i<528;i++){
if(pack[i].flag==2){
painter.setBrush(Qt::NoBrush);
QBrush brush(Qt::red);
painter.setBrush(brush);
painter.drawRect(pack[i].x1*12+30,pack[i].y1*12+100,pack[i].temp*12,pack[i].temp*12);
}
else if(pack[i].flag==1){
for(int ii=0;ii<pack[i].tem.size();ii++){
painter.setBrush(Qt::NoBrush);
painter.setPen(Qt::NoPen);
if(pack[i].tem[ii].flag==2){
QPen pen2(QColor(0,0,0));
painter.setPen(pen2);
QBrush brush2(Qt::red);
painter.setBrush(brush2);
painter.drawRect(pack[i].tem[ii].x1*12+30,pack[i].tem[ii].y1*12+100,pack[i].tem[ii].temp*12,pack[i].tem[ii].temp*12);
}
else if(pack[i].tem[ii].flag==0){
painter.setBrush(Qt::NoBrush);
painter.setPen(Qt::NoPen);
QPen pen2(QColor(0,0,0));
painter.setPen(pen2);
painter.drawRect(pack[i].tem[ii].x1*12+30,pack[i].tem[ii].y1*12+100,pack[i].tem[ii].temp*12,pack[i].tem[ii].temp*12);
}
else{
painter.setBrush(Qt::NoBrush);
painter.setPen(Qt::NoPen);
QPen pen2(QColor(0,0,0));
painter.setPen(pen2);
QBrush brush2(Qt::blue);
painter.setBrush(brush2);
painter.drawRect(pack[i].tem[ii].x1*12+30,pack[i].tem[ii].y1*12+100,pack[i].tem[ii].temp*12,pack[i].tem[ii].temp*12);
}
}
}
painter.setPen(Qt::NoPen);
}
painter.setBrush(Qt::NoBrush);
painter.setPen(Qt::NoPen);
for(int j=0;j<lastxin[shu11].weixing.size();j++){
QPen pen2(QColor(255,255,255));
painter.setPen(pen2);
painter.drawEllipse(QPoint((lastxin[shu11].weixing[j].x1-75)*12+30,lastxin[shu11].weixing[j].y1*12+100),7*12,7*12);
}
painter.setPen(Qt::NoPen);
}
if(anniu==2||fangying==1){
for(int i=0;i<528;i++){
if(pack[i].flag==2){
painter.setBrush(Qt::NoBrush);
QBrush brush(Qt::red);
painter.setBrush(brush);
painter.drawRect(pack[i].x1*12+30,pack[i].y1*12+100,pack[i].temp*12,pack[i].temp*12);
}
else if(pack[i].flag==1){
for(int ii=0;ii<pack[i].tem.size();ii++){
painter.setBrush(Qt::NoBrush);
painter.setPen(Qt::NoPen);
if(pack[i].tem[ii].flag==2){
QPen pen2(QColor(0,0,0));
painter.setPen(pen2);
QBrush brush2(Qt::red);
painter.setBrush(brush2);
painter.drawRect(pack[i].tem[ii].x1*12+30,pack[i].tem[ii].y1*12+100,pack[i].tem[ii].temp*12,pack[i].tem[ii].temp*12);
}
else if(pack[i].tem[ii].flag==0){
painter.setBrush(Qt::NoBrush);
painter.setPen(Qt::NoPen);
QPen pen2(QColor(0,0,0));
painter.setPen(pen2);
painter.drawRect(pack[i].tem[ii].x1*12+30,pack[i].tem[ii].y1*12+100,pack[i].tem[ii].temp*12,pack[i].tem[ii].temp*12);
}
else{
painter.setBrush(Qt::NoBrush);
painter.setPen(Qt::NoPen);
QPen pen2(QColor(0,0,0));
painter.setPen(pen2);
QBrush brush2(Qt::blue);
painter.setBrush(brush2);
painter.drawRect(pack[i].tem[ii].x1*12+30,pack[i].tem[ii].y1*12+100,pack[i].tem[ii].temp*12,pack[i].tem[ii].temp*12);
}
}
}
painter.setPen(Qt::NoPen);
}
}
}
void MainWindow::mousePressEvent(QMouseEvent*event){
qDebug()<<event->pos();
}
void MainWindow::firque(){
miao zutime[13];//存放13个城市的24小时
for(int ii=0;ii<9;ii++){
QFile file(Wname[ii]);//经验证,九个文件是成功打开了的
if (file.open(QIODevice::ReadOnly | QIODevice::Text))
{
double yuan1=0,yuan2=0,yuan3=0,yuan4=0;
int jilua=-1,jiluc=0,miaoshu=0;
//yuan1,2,3,4分别用于存储该时刻圆的上下两个点,方便计算圆心。
QString jilutime;//存储2020/1/1 00:00:00
double r=7.0068;//经过验算,所有卫星的半径皆为7.0068
while (!file.atEnd())
{
QByteArray line = file.readLine();
QString str = QString(line);
QString ss="/";//需通过制表符或者空格来分开同一行的经纬度值,/代表是下一时刻的开始
int weizhi=str.indexOf(ss);
if(weizhi!=-1){
jiluc=0,jilua++;
jilutime=str;
int kongg=str.indexOf(" ");//此处用于计算该圆是处于哪一个时刻,好放进第三题数组里
int dian1=str.indexOf(":");
int dian2=str.indexOf(":",str.indexOf(":")+1);
QString st1="",st2="",st3="";
if((dian1-kongg)==2)
st1+=str[kongg+1];
else{
st1+=str[kongg+1];
st1+=str[kongg+2];
}
st2+=str[dian1+1];
st2+=str[dian1+2];
st3+=str[dian2+1];
st3+=str[dian2+2];
miaoshu=st1.toInt()*60*60+st2.toInt()*60+st3.toInt();
continue;
}
else{
//否则该行即为坐标行
jiluc++;
if(jiluc!=1&&jiluc!=11)
continue;
QString kongge=" ",tab0=" ";//空格符与制表符
int kw=str.indexOf(kongge);//查找空格符位置
int tw=str.indexOf(tab0);//制表符位置
if(kw==-1)//没找到空格符代表该行是两个制表符
kw=str.indexOf(tab0,tw+1);
QString num0="",num1="";
for(int i0=1;i0<kw;i0++){
if(i0==1&&str[i0]=="-")
continue;
num0+=str[i0];//经度
}
for(int i0=kw+1;i0<kw+12;i0++){
num1+=str[i0];//纬度
}
double n1=num0.toDouble(),n2=num1.toDouble();
if(jiluc==1){
yuan1=n1;
yuan2=n2;
continue;
}
if(jiluc==11){
yuan3=n1;
yuan4=n2;
}
if(jiluc==11){
double x1=(double)(yuan1+yuan3)/(double)2;
double y1=(double)(yuan2+yuan4)/(double)2;//得到了此时刻圆心位置
xing ad1;ad1.x1=x1;ad1.y1=y1;
alltime[miaoshu].weixing.push_back(ad1);
if(x1<=maxx&&x1>=minn&&y1>=min1&&y1<=max1){
xing ad;
ad.x1=x1;
ad.y1=y1;
lastxin[miaoshu].weixing.push_back(ad);//将对应秒数下能够覆盖矩形的一部分的圆心存储进来
}
for(int i=0;i<13;i++){
double bx,by;
if(x1>cn.team[i].jing)
bx=x1-cn.team[i].jing;
else
bx=cn.team[i].jing-x1;
if(y1>cn.team[i].wei)
by=y1-cn.team[i].wei;
else
by=cn.team[i].wei-y1;
bool pa1=0;
if((bx*bx+by*by)<=49.0882){
pa1=1;
}
if(pa1){//该城市此刻在该园内
zutime[i].num[jilua]=true;
//qDebug()<<"a";
zutime[i].jilu++;
if(zutime[i].jilu==0){//城市第一次进入圆
QString as=" from";
as+=jilutime;
zutime[i].shijian+=as;
}
}
else{
if(zutime[i].jilu!=-1){
if(zutime[i].jilu>zutime[i].max){
zutime[i].max=zutime[i].jilu+1;
}
if(zutime[i].jilu<zutime[i].min)
zutime[i].min=zutime[i].jilu+1;
zutime[i].pingjun+=zutime[i].jilu+1;
zutime[i].jilu=-1;
QString as="to";
as+=jilutime;
//qDebug()<<jilutime;
zutime[i].shijian+=as;
}
}
}
}
}
}
file.close();
}
}
for(int i=0;i<13;i++){
xinxi[i]=zutime[i].shijian;
xinxi[i]+="max:";
xinxi[i]+=QString::number(zutime[i].max);
xinxi[i]+='\n';
xinxi[i]+="min:";
xinxi[i]+=QString::number(zutime[i].min);
xinxi[i]+='\n';
xinxi[i]+="all:";
xinxi[i]+=QString::number(zutime[i].pingjun);
}
}
void MainWindow::lastque(){
int jilu5=-1;
for(int ii=0;ii<9;ii++){
QFile file(Wname[ii]);//经验证,九个文件是成功打开了的
if (file.open(QIODevice::ReadOnly | QIODevice::Text))
{
int jiluc=0,miaoshu=0;//miaoshu用于记录当前的圆是在第几秒
double yuan1,yuan2,yuan3,yuan4;
while (!file.atEnd())
{
QByteArray line = file.readLine();
QString str = QString(line);
QString ss="/";//需通过制表符或者空格来分开同一行的经纬度值,/代表是下一时刻的开始
int weizhi=str.indexOf(ss);
if(weizhi!=-1){
jiluc=0;
int kongg=str.indexOf(" ");//此处用于计算该圆是处于哪一个时刻,好放进第三题数组里
int dian1=str.indexOf(":");
int dian2=str.indexOf(":",str.indexOf(":")+1);
QString st1="",st2="",st3="";
if((dian1-kongg)==2)
st1+=str[kongg+1];
else{
st1+=str[kongg+1];
st1+=str[kongg+2];
}
st2+=str[dian1+1];
st2+=str[dian1+2];
st3+=str[dian2+1];
st3+=str[dian2+2];
miaoshu=st1.toInt()*60*60+st2.toInt()*60+st3.toInt();
continue;
}
else{
//否则该行即为坐标行
jiluc++;
if(jiluc!=1&&jiluc!=11)
continue;
QString kongge=" ",tab0=" ";//空格符与制表符
int kw=str.indexOf(kongge);//查找空格符位置
int tw=str.indexOf(tab0);//制表符位置
if(kw==-1)//没找到空格符代表该行是两个制表符
kw=str.indexOf(tab0,tw+1);
QString num0="",num1="";
for(int i0=1;i0<kw;i0++){
if(i0==1&&str[i0]=="-")
continue;
num0+=str[i0];//经度
}
for(int i0=kw+1;i0<kw+12;i0++){
num1+=str[i0];//纬度
}
double n1=num0.toDouble(),n2=num1.toDouble();
if(jiluc==1){
yuan1=n1;
yuan2=n2;
continue;
}
if(jiluc==11){
yuan3=n1;
yuan4=n2;
}
if(jiluc==11){
double x1=(double)(yuan1+yuan3)/(double)2;
double y1=(double)(yuan2+yuan4)/(double)2;//得到了此时刻圆心位置
if(x1<=maxx&&x1>=minn&&y1>=min1&&y1<=max1){
xing ad;
ad.x1=x1;
ad.y1=y1;
lastxin[miaoshu].weixing.push_back(ad);//将对应秒数下能够覆盖矩形的一部分的圆心存储进来
}
}
}
}
file.close();
}
}
}
void MainWindow::qiujianxi(){
for(int i=0;i<13;i++){
int flagd=0,flagf=0,flagg=0,flagh=0;//分别用于判断4个状态以及存储最大时间间隙
for(int i1=0;i1<86400;i1++){
int flags=0;
for(int j=0;j<alltime[i1].weixing.size();j++){
double cha1,cha2;
if(cn.team[i].jing>alltime[i1].weixing[j].x1)
cha1=cn.team[i].jing-alltime[i1].weixing[j].x1;
else
cha1=alltime[i1].weixing[j].x1-cn.team[i].jing;
if(cn.team[i].wei>alltime[i1].weixing[j].y1)
cha2=cn.team[i].wei-alltime[i1].weixing[j].y1;
else
cha2=alltime[i1].weixing[j].y1-cn.team[i].wei;
bool pa1=0;
if((cha1*cha1+cha2*cha2)<=49.0882){
pa1=1;
}
if(pa1){
flags=1;
//qDebug()<<"size"<<cunfang2[i].weixing.size();size里是有东西的,这儿无错
}
}
if(flags==0&&flagd==0){//代表此时处于时间间隙
flagf++;
}
else if(flags==0&&flagd==1){//代表前一秒处于时间窗口,此时进入时间间隙
flagd=0;
flagf++;
}
else if(flags==1&&flagd==1){//代表处于时间窗口内
}
else if(flags==1&&flagd==0){//代表前一秒处于时间间隙,此时处于时间窗口
if(flagf>flagg)
flagg=flagf;
flagh+=flagf;
flagd=1;
flagf=0;
}
}
xinxi[i]+='\n';
xinxi[i]+="时间间隙最大值:";
xinxi[i]+=QString::number(flagg);
xinxi[i]+='\n';
xinxi[i]+="时间间隙累计值:";
xinxi[i]+=QString::number(flagh);
}
}
//以下六个函数用于计算网格是否在园中
void MainWindow::chushihua(){
double henga=0,zonga=0,fla=0;
for(int i=0;i<528;i++){
pack[i].x1=henga;
pack[i].y1=zonga;
pack[i].temp=2.5;
henga+=2.5;
fla++;
if(fla==24){
fla=0;
henga=0;
zonga+=2.5;
}
}
}
void MainWindow::tiaozheng(double x1,double y1,int&x2,int&y2){
int s1,s2,s3;
if(x1<=0){
s1=0;
}//在左边界外
else {//在内部或右边界外
if(x1-7.0063<=0){//圆心靠近左边界
s1=0;
}
else{
int temp1=(x1-7.0063);
temp1*=10;
while(true){
if(temp1<50){
temp1=0;
break;
}
else if(temp1%25!=0){
temp1-=10;
}
else
break;
}
temp1/=10;
s1=temp1;
}
}
if(y1<=0){
s2=0;
}
else{
if(y1-7.0063<=0){
s2=0;
}
else{
int temp1=(y1-7.0063);
temp1*=10;
int temp2=(y1+7.0063);
temp2*=10;
while(true){
if(temp1<50){
temp1=0;
break;
}
else if(temp1%25!=0){
temp1-=10;
}
else
break;
}
while(true){
if(temp2>550){
temp2=550;
break;
}
else if(temp2%25!=0){
temp2+=10;
}
else
break;
}
temp1/=10;
temp2/=10;
s2=temp1;
s3=temp2;
}
}
s1/=2.5;
s2/=2.5;
s3/=2.5;
int s4=s1+8;
if(s4>23)
s4=23;
if(s3==22)
s3=21;
x2=s2*24+s1-1;
y2=s3*24+s4;
}
int MainWindow::panduan(gezi&x,double x1,double y1){//小网格
double qw1,qw2,qw3,qw4,qw5,qw6,qw7,qw8;
if(x.x1>x1){
qw1=x.x1-x1;
}
else{
qw1=x1-x.x1;
}
if(x.y1>y1){
qw2=x.y1-y1;
}
else{
qw2=y1-x.y1;
}
if((x.x1+x.temp)>x1){
qw3=x.x1+x.temp-x1;
}
else{
qw3=x1-x.x1-x.temp;
}
qw4=qw2;
if((x.y1+x.temp)>y1){
qw6=x.y1+x.temp-y1;
}
else{
qw6=y1-x.y1-x.temp;
}
qw5=qw1;
qw7=qw3;
qw8=qw6;
bool pa1=0,pa2=0,pa3=0,pa4=0;
if((qw1*qw1+qw2*qw2)<=49.0882){
pa1=1;
}
if((qw3*qw3+qw4*qw4)<=49.0882){
pa2=1;
}
if((qw5*qw5+qw6*qw6)<=49.0882){
pa3=1;
}
if((qw7*qw7+qw8*qw8)<=49.0882){
pa4=1;
}
if(pa1&&pa2&&pa3&&pa4){
x.flag=2;
return 2;
}
else{
if(!pa1&&!pa2&&!pa3&&!pa4){
return 0;
}
else{
if(x.flag!=2)
x.flag=1;
return 1;
}
}
}
int MainWindow::panduan2(gezi2 &x, double x1, double y1){//大网格
double qw1,qw2,qw3,qw4,qw5,qw6,qw7,qw8;
if(x.x1>x1){
qw1=x.x1-x1;
}
else{
qw1=x1-x.x1;
}
if(x.y1>y1){
qw2=x.y1-y1;
}
else{
qw2=y1-x.y1;
}
if((x.x1+x.temp)>x1){
qw3=x.x1+x.temp-x1;
}
else{
qw3=x1-x.x1-x.temp;
}
qw4=qw2;
if((x.y1+x.temp)>y1){
qw6=x.y1+x.temp-y1;
}
else{
qw6=y1-x.y1-x.temp;
}
qw5=qw1;
qw7=qw3;
qw8=qw6;
bool pa1=0,pa2=0,pa3=0,pa4=0;
if((qw1*qw1+qw2*qw2)<=49.0882){
pa1=1;
}
if((qw3*qw3+qw4*qw4)<=49.0882){
pa2=1;
}
if((qw5*qw5+qw6*qw6)<=49.0882){
pa3=1;
}
if((qw7*qw7+qw8*qw8)<=49.0882){
pa4=1;
}
if(pa1&&pa2&&pa3&&pa4){
x.flag=2;
return 2;
}
else{
if(!pa1&&!pa2&&!pa3&&!pa4){
return 0;
}
else{
if(x.flag!=2)
x.flag=1;
return 1;
}
}
}
void MainWindow::huafen(double x1,double y1){
int i1,i2;
tiaozheng(x1,y1,i1,i2);
for(int i=0;i<528;i++){
if(pack[i].flag==2)
continue;
else if(pack[i].flag==1){
int zhong1;
zhong1=panduan2(pack[i],x1,y1);
if(zhong1==1)
huafen2(pack[i],x1,y1);
else if(zhong1==2){
pack[i].tem.clear();
}
else
pack[i].flag=1;
}
else{//还未被其他圆占领
int zhong1=panduan2(pack[i],x1,y1);
if(zhong1==1){
gezi a,b,c,d;
a.x1=pack[i].x1;
a.y1=pack[i].y1;
a.temp=pack[i].temp/2;
pack[i].tem.push_back(a);
b.x1=pack[i].x1+a.temp;
b.y1=pack[i].y1;
b.temp=a.temp;
pack[i].tem.push_back(b);
c.x1=pack[i].x1;
c.y1=pack[i].y1+a.temp;
c.temp=a.temp;
pack[i].tem.push_back(c);
d.x1=pack[i].x1+a.temp;
d.y1=pack[i].y1+a.temp;
d.temp=a.temp;
pack[i].tem.push_back(d);
huafen2(pack[i],x1,y1);
}
}
}
}
void MainWindow::huafen2(gezi2&temp, double x1, double y1){
for(int i=0;i<temp.tem.size();i++){
if(temp.tem[i].flag==2)
continue;
else if(temp.tem[i].temp>0.625){//最多分至每个网格边长为0.625
int zhong1=panduan(temp.tem[i],x1,y1);
//if(jilu1>temp.tem[i].flag)//如果从半覆盖变成了不在圆内,变回半覆盖
//temp.tem[i].flag=jilu1;
if(zhong1==1){
gezi a,b,c,d;
a.x1=temp.tem[i].x1;
a.y1=temp.tem[i].y1;
a.temp=temp.tem[i].temp/2;
temp.tem.push_back(a);
b.x1=temp.tem[i].x1+a.temp;
b.y1=temp.tem[i].y1;
b.temp=a.temp;
temp.tem.push_back(b);
c.x1=temp.tem[i].x1;
c.y1=temp.tem[i].y1+a.temp;
c.temp=a.temp;
temp.tem.push_back(c);
d.x1=temp.tem[i].x1+a.temp;
d.y1=temp.tem[i].y1+a.temp;
d.temp=a.temp;
temp.tem.push_back(d);
for(auto it=temp.tem.begin();it<temp.tem.end();it++){
if(it->x1==temp.tem[i].x1&&it->y1==temp.tem[i].y1&&it->temp==temp.tem[i].temp){
temp.tem.erase(it);
i--;
break;
}
}
}
}
else if(temp.tem[i].temp<=0.625){
int jilu1=temp.tem[i].flag;
panduan(temp.tem[i],x1,y1);
if(jilu1>temp.tem[i].flag)//如果从半覆盖变成了不在圆内,变回半覆盖
temp.tem[i].flag=jilu1;
}
}
}
void MainWindow::timerEvent(QTimerEvent *event){
if(fangying==1){
for(int i=0;i<528;i++){
pack[i].flag=0;
pack[i].tem.clear();
}
for(int i1=0;i1<lastxin[id3].weixing.size();i1++){
huafen(lastxin[id3].weixing[i1].x1-75,lastxin[id3].weixing[i1].y1);
}
id3++;
if(id3==86400)
id3=0;
repaint();
}
}